第20章 数据的分析小结与复习 课件(共22张PPT)
文档属性
| 名称 | 第20章 数据的分析小结与复习 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 07:18:41 | ||
图片预览





文档简介
(共22张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第二十章 数据的分析
第20章数据的分析
小结与复习
理解并会计算加权平均数、众数、中位数,能选择合适的量描述数据的集中程度;理解并会计算方差并会用它描述数据的离散程度;体会用样本估计总体的思想,会用样本平均数,方差估计总体平均数,方差.
核心素养目标:
经历探索数据的收集、整理、分析过程,在活动中发展学生的统计意识和数据处理的方法与能力.
培养合作交流的意识与能力,提高解决简单的实际问题能力,形成一定的数据意识和解决问题的能力,体会特征数据的应用价值
在生产和生活中,为了解总体的情况,我们经常从总体中抽取样本,通过对样本数据的处理,获得一些结论,然后再利用这些结论对总体进行估计.这就是用样本估计总体,它是统计的基本思想.
在整理、描述和分析样本数据时,我们可以通过绘制图表,如条形图、折线图、扇形图和直方图等获得一些信息.还可以通过计算反映数据某方面特征的量获得更多的信息,如利用平均数、中位数和众数,刻画数据的集中趋势;利用方差刻画数据的波动程度.
平均数、中位数和众数从不同侧面反映了一组数据的集中趋势.因此,用它们刻画数据时,要根据统计调查的目的和具体间题的特点进行选择.
回顾与思考:
请你带着下面的问题,复习一下全章的内容吧.
1.举例说明平均数、中位数、众数的意义.
2.算术平均数与加权平均数有什么联系和区别 举例说明加权平均数中“权”的意义.
3,举例说明怎样用方差刻画数据的波动程度.
4.举例说明刻画数据特征的量在决策中的作用.
5.搜集关于“统计学”方面的资料(如学科发展史、思想方法、人物等),从某个角度谈谈你对统计的认识.
回顾与思考:
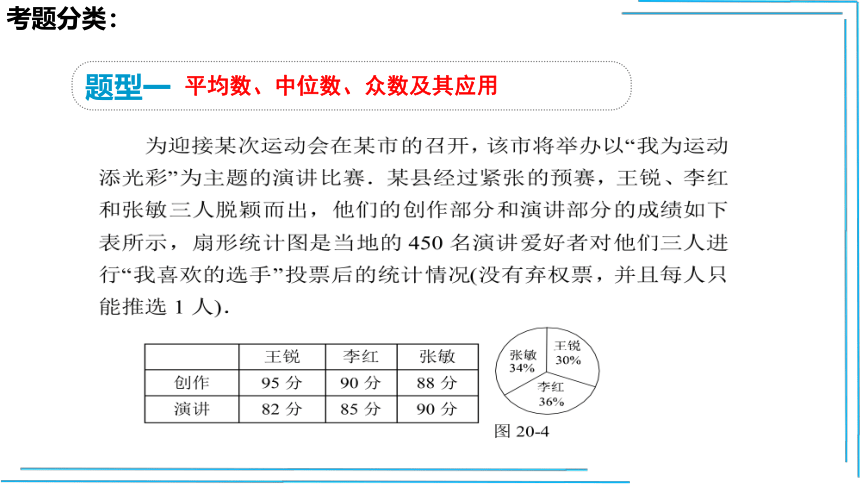
题型一
平均数、中位数、众数及其应用
考题分类:
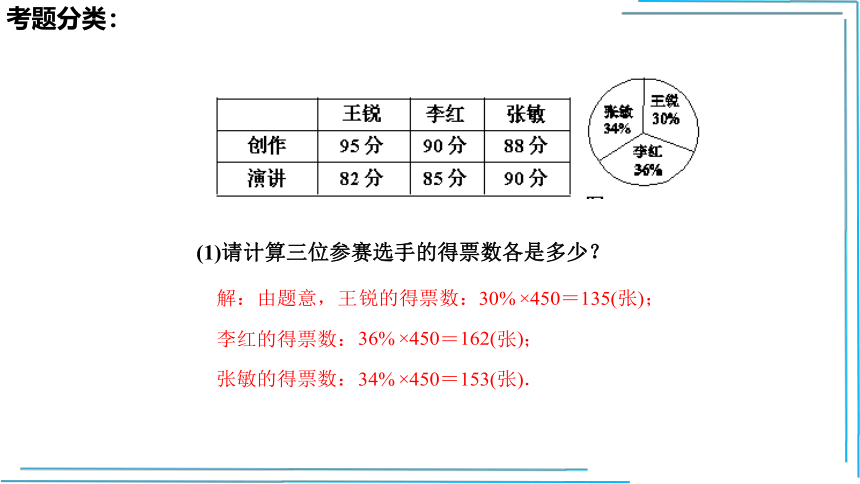
(1)请计算三位参赛选手的得票数各是多少?
考题分类:
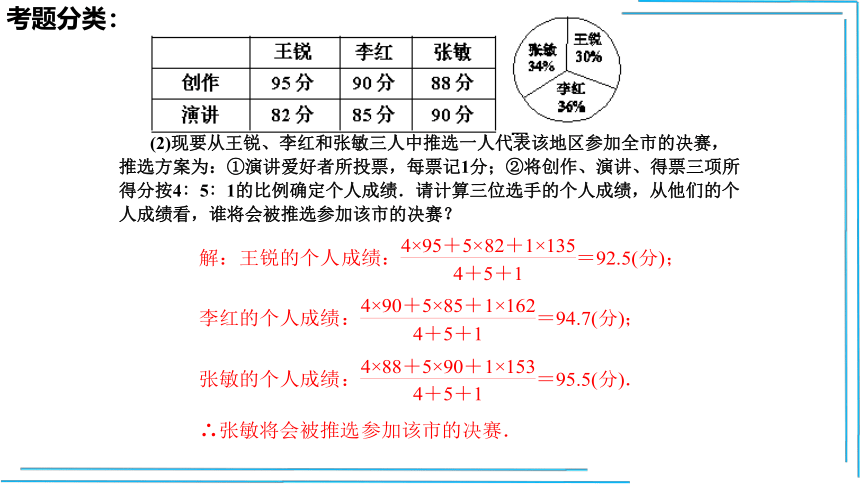
(2)现要从王锐、李红和张敏三人中推选一人代表该地区参加全市的决赛,推选方案为:①演讲爱好者所投票,每票记1分;②将创作、演讲、得票三项所得分按4∶5∶1的比例确定个人成绩.请计算三位选手的个人成绩,从他们的个人成绩看,谁将会被推选参加该市的决赛?
考题分类:
1.在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示,是其中的甲、乙台阶的示意图,请你用学过的统计知识回答下列问题:
15
16
16
14
14
15
15
11
18
17
10
19
甲路段
乙路段
(1)两段台阶路有哪些相同点和不同点?
解:
相同点:两段台阶的平均高度相同;
不同点:两段台阶的中位数、方差和极差不同.
题型二
极差、方差及其应用
考题分类:
15
16
16
14
14
15
15
11
18
17
10
19
甲路段
乙路段
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路,对于这两段台阶,在台阶数不变的情况下,请你提出合理的整修建议.
解:使每个台阶的高度均为15cm,使得方差为0.
解:甲台阶走起来更舒服些,因为它的台阶高度的方差小.
考题分类:
题型三
数据分析的应用
1. 2014年7月25日全国青少年校园足球比赛落幕,某学校为了解本校2400名学生对本次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图1-1)、扇形统计图(图1-2)和折线统计图(图2).
考题分类:
(1)本次共随机抽查了 名学生,根据信息补全图(1-1)中条形统计图,图(1-2)中八年级所对应扇形的圆心角的度数为 ;
200
144°
补全如图
考题分类:
(2)如果把“特别关注”、“一般关注”、“偶尔关注”都看作成关注,那么全校关注足球赛的学生大约有多少名?
(2)根据题意得:关注的学生所占的百分比为,
所以全校关注足球赛的学生大约有2400×55%=1320 (人);
考题分类:
(3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议;
(3)①根据以上所求可得出:只有55%的学生关注足球,有45%的学生不关注,可以看出仍有部分学生忽略了足球的关注,希望学校做好教育与引导工作,加大对足球进校园的宣传力度,让校园足球得到更多的关注和支持,推动校园足球的发展.
考题分类:
(3)②如果要了解学校中小学生校园足球的关注情况,你认为应该如何进行抽样?
②考虑到样本具有的随机性、代表性、广泛性,如果要了解中小学生对足球的关注的情况,抽样时应针对不同的年级、不同性别、不同年龄段的学生进行随机抽样.
考题分类:
1.某米店经营某种品牌的大米,该店记录了一周中不同包装(10 kg,20 kg,50 kg)的大米的销售量(单位:袋)如下:10 kg装100袋;20 kg装220袋;50 kg装80袋.如果每500 g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的( )
A.平均数 B.中位数 C.众数 D.最大值
C
A
2.一组数据中的一个数大小发生了变化,一定会影响这组数据的平均数、众数、中位数中的( )
A.1个 B.2个 C.3个 D.0个
跟踪练习:
3.某地发生地震灾害后,某中学八(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10 B.10,20
C.16,15 D.15,16
B
跟踪练均数
数据的分析
数据
的集
中趋势
中位数
众 数
方 差
数据的波动程度
用样本估计总体
将一组数据按由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处在中间位置的数为这组数据的中位数;如果数据的个数是偶数,则中间两个数的平均数为这组数据的中位数
一组数据中出现次数最多的数据就是这组数据的众数
方差越大,数据的波动越大;
方差越小,数据的波动越小
用样本平均数估计总体平均数
用样本方差估计总体方差
若n个数的平均数是,则这n个数据的方差为
若n个数x1,x2,…xn的个数分别是w1,w2,…
wn, 则 叫做这n个数的
加权平均数
知识总结:
课后作业:
必做题:教材第136~137页复习题20第1、2 、3、4、5题
选做题:教材第137页复习题第6、7、8、9题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第二十章 数据的分析
第20章数据的分析
小结与复习
理解并会计算加权平均数、众数、中位数,能选择合适的量描述数据的集中程度;理解并会计算方差并会用它描述数据的离散程度;体会用样本估计总体的思想,会用样本平均数,方差估计总体平均数,方差.
核心素养目标:
经历探索数据的收集、整理、分析过程,在活动中发展学生的统计意识和数据处理的方法与能力.
培养合作交流的意识与能力,提高解决简单的实际问题能力,形成一定的数据意识和解决问题的能力,体会特征数据的应用价值
在生产和生活中,为了解总体的情况,我们经常从总体中抽取样本,通过对样本数据的处理,获得一些结论,然后再利用这些结论对总体进行估计.这就是用样本估计总体,它是统计的基本思想.
在整理、描述和分析样本数据时,我们可以通过绘制图表,如条形图、折线图、扇形图和直方图等获得一些信息.还可以通过计算反映数据某方面特征的量获得更多的信息,如利用平均数、中位数和众数,刻画数据的集中趋势;利用方差刻画数据的波动程度.
平均数、中位数和众数从不同侧面反映了一组数据的集中趋势.因此,用它们刻画数据时,要根据统计调查的目的和具体间题的特点进行选择.
回顾与思考:
请你带着下面的问题,复习一下全章的内容吧.
1.举例说明平均数、中位数、众数的意义.
2.算术平均数与加权平均数有什么联系和区别 举例说明加权平均数中“权”的意义.
3,举例说明怎样用方差刻画数据的波动程度.
4.举例说明刻画数据特征的量在决策中的作用.
5.搜集关于“统计学”方面的资料(如学科发展史、思想方法、人物等),从某个角度谈谈你对统计的认识.
回顾与思考:
题型一
平均数、中位数、众数及其应用
考题分类:
(1)请计算三位参赛选手的得票数各是多少?
考题分类:
(2)现要从王锐、李红和张敏三人中推选一人代表该地区参加全市的决赛,推选方案为:①演讲爱好者所投票,每票记1分;②将创作、演讲、得票三项所得分按4∶5∶1的比例确定个人成绩.请计算三位选手的个人成绩,从他们的个人成绩看,谁将会被推选参加该市的决赛?
考题分类:
1.在某旅游景区上山的一条小路上,有一些断断续续的台阶,如图所示,是其中的甲、乙台阶的示意图,请你用学过的统计知识回答下列问题:
15
16
16
14
14
15
15
11
18
17
10
19
甲路段
乙路段
(1)两段台阶路有哪些相同点和不同点?
解:
相同点:两段台阶的平均高度相同;
不同点:两段台阶的中位数、方差和极差不同.
题型二
极差、方差及其应用
考题分类:
15
16
16
14
14
15
15
11
18
17
10
19
甲路段
乙路段
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路,对于这两段台阶,在台阶数不变的情况下,请你提出合理的整修建议.
解:使每个台阶的高度均为15cm,使得方差为0.
解:甲台阶走起来更舒服些,因为它的台阶高度的方差小.
考题分类:
题型三
数据分析的应用
1. 2014年7月25日全国青少年校园足球比赛落幕,某学校为了解本校2400名学生对本次足球赛的关注程度,以利于做好教育和引导工作,随机抽取了本校内的六、七、八、九四个年级部分学生进行调查,按“各年级被抽取人数”与“关注程度”,分别绘制了条形统计图(图1-1)、扇形统计图(图1-2)和折线统计图(图2).
考题分类:
(1)本次共随机抽查了 名学生,根据信息补全图(1-1)中条形统计图,图(1-2)中八年级所对应扇形的圆心角的度数为 ;
200
144°
补全如图
考题分类:
(2)如果把“特别关注”、“一般关注”、“偶尔关注”都看作成关注,那么全校关注足球赛的学生大约有多少名?
(2)根据题意得:关注的学生所占的百分比为,
所以全校关注足球赛的学生大约有2400×55%=1320 (人);
考题分类:
(3)①根据上面的统计结果,谈谈你对该校学生对足球关注的现状的看法及建议;
(3)①根据以上所求可得出:只有55%的学生关注足球,有45%的学生不关注,可以看出仍有部分学生忽略了足球的关注,希望学校做好教育与引导工作,加大对足球进校园的宣传力度,让校园足球得到更多的关注和支持,推动校园足球的发展.
考题分类:
(3)②如果要了解学校中小学生校园足球的关注情况,你认为应该如何进行抽样?
②考虑到样本具有的随机性、代表性、广泛性,如果要了解中小学生对足球的关注的情况,抽样时应针对不同的年级、不同性别、不同年龄段的学生进行随机抽样.
考题分类:
1.某米店经营某种品牌的大米,该店记录了一周中不同包装(10 kg,20 kg,50 kg)的大米的销售量(单位:袋)如下:10 kg装100袋;20 kg装220袋;50 kg装80袋.如果每500 g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的( )
A.平均数 B.中位数 C.众数 D.最大值
C
A
2.一组数据中的一个数大小发生了变化,一定会影响这组数据的平均数、众数、中位数中的( )
A.1个 B.2个 C.3个 D.0个
跟踪练习:
3.某地发生地震灾害后,某中学八(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10 B.10,20
C.16,15 D.15,16
B
跟踪练均数
数据的分析
数据
的集
中趋势
中位数
众 数
方 差
数据的波动程度
用样本估计总体
将一组数据按由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处在中间位置的数为这组数据的中位数;如果数据的个数是偶数,则中间两个数的平均数为这组数据的中位数
一组数据中出现次数最多的数据就是这组数据的众数
方差越大,数据的波动越大;
方差越小,数据的波动越小
用样本平均数估计总体平均数
用样本方差估计总体方差
若n个数的平均数是,则这n个数据的方差为
若n个数x1,x2,…xn的个数分别是w1,w2,…
wn, 则 叫做这n个数的
加权平均数
知识总结:
课后作业:
必做题:教材第136~137页复习题20第1、2 、3、4、5题
选做题:教材第137页复习题第6、7、8、9题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
