1.3 探索三角形全等的条件(第7课时)课件(27张PPT)
文档属性
| 名称 | 1.3 探索三角形全等的条件(第7课时)课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第1章 · 全等三角形
1.3 探索三角形全等的条件
第7课时 用圆规、直尺作角平分线及过已知点作已知直线的垂线
学习目标
会用直尺和圆规作角平分线以及过已知直线外一点作这条直线的垂线, 并能说出作图的依据.
知识回顾
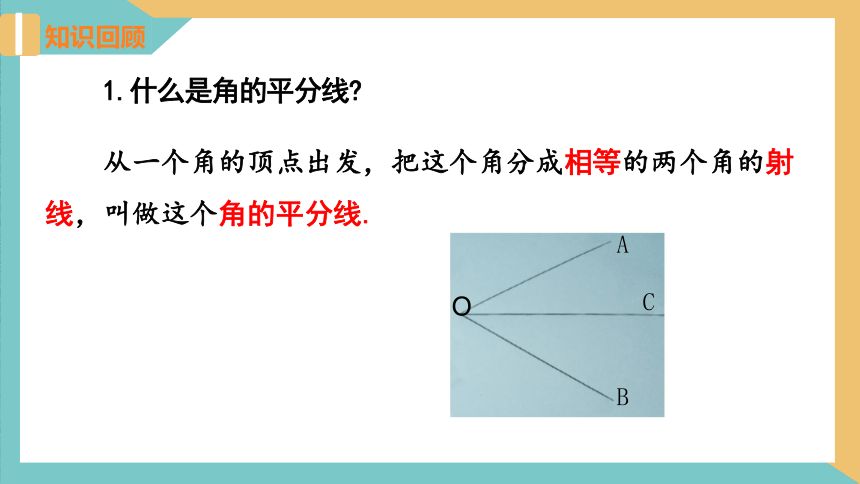
1.什么是角的平分线
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
A
B
O
C
知识回顾
2.你能找出一个角的平分线吗?
方法一:对折
方法二:用量角器
如果在黑板、墙壁呢?
如果画22.5°的角平分线,测量11.25°时,是不是不够精确呢?
怎样更精确地平分
一个角呢?
新知探索
工人师傅常用角尺平分一个角.
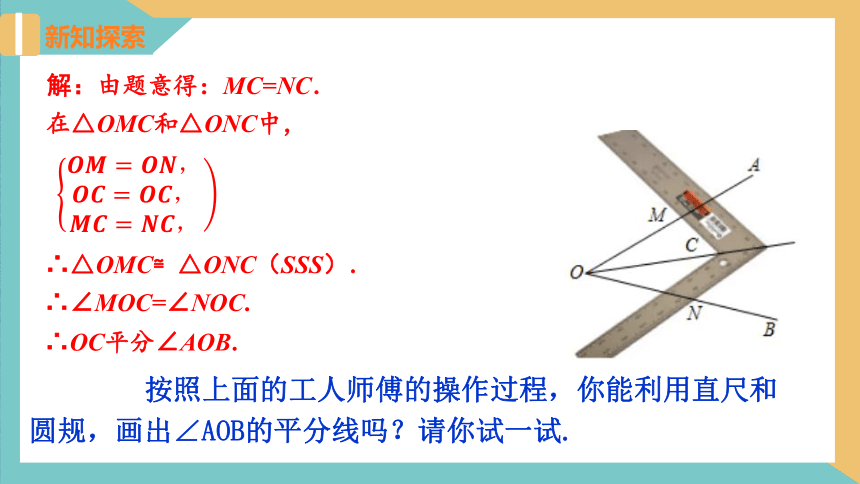
如图,在∠AOB的两边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,这时过角尺顶点C连OC,射线OC就是∠AOB的平分线.
你能说明这样画角平分线的道理吗?
数学来源于生活,古代的能工巧匠就找到了解决的办法.
解:由题意得:MC=NC.
在△OMC和△ONC中,
∴△OMC≌△ONC(SSS).
新知探索
∴∠MOC=∠NOC.
∴OC平分∠AOB.
按照上面的工人师傅的操作过程,你能利用直尺和圆规,画出∠AOB的平分线吗?请你试一试.
新知探索
已知:∠AOB.
求作:∠AOB的平分线.
A
B
M
N
C
O
作法:
1.以____为圆心,________为半径作弧,分别交射线OA、OB于点M、N;
O
任意长
2.分别点以_______为圆心,________的长为半径作弧,两弧在∠AOB的内部交于点___.
M、N
大于MN
C
3.作射线______.
OC
OC就是∠AOB的平分线.
新知探索
A
B
M
N
C
O
E
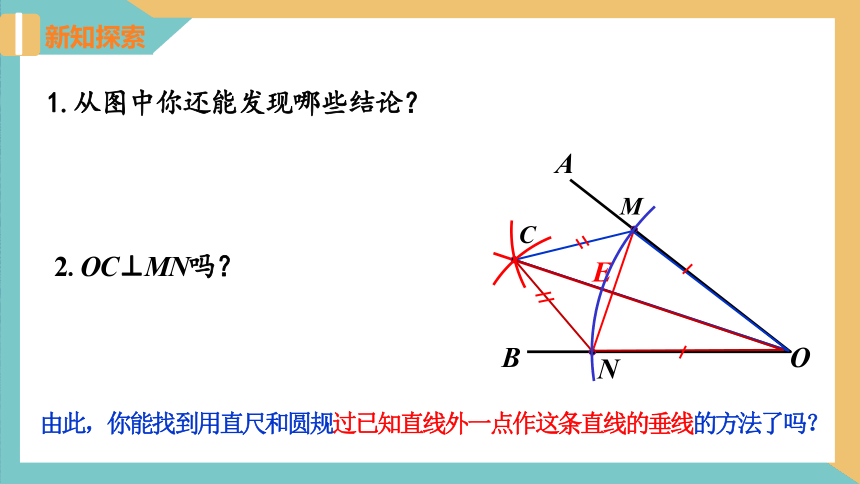
1.从图中你还能发现哪些结论?
2.OC⊥MN吗?
由此,你能找到用直尺和圆规过已知直线外一点作这条直线的垂线的方法了吗?
新知探索
A
B
P
C
D
Q
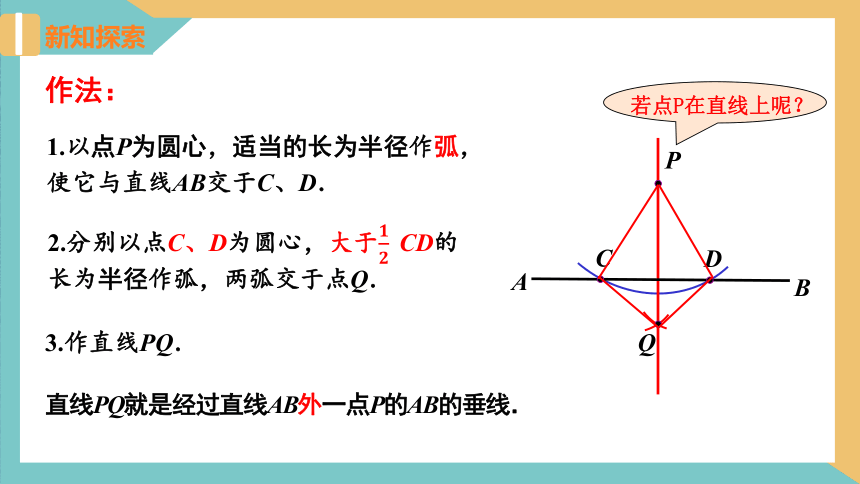
作法:
3.作直线PQ.
1.以点P为圆心,适当的长为半径作弧,使它与直线AB交于C、D.
直线PQ就是经过直线AB外一点P的AB的垂线.
2.分别以点C、D为圆心,大于CD的长为半径作弧,两弧交于点Q.
若点P在直线上呢?
新知探索
A
B
P
C
D
作法:
3.作直线PQ.
1.以点P为圆心,适当的长为半径作弧,使它与直线AB交于C、D.
直线PQ就是经过直线AB上一点P的AB的垂线.
2.分别以点C、D为圆心,大于CD的长为半径作弧,两弧交于点Q.
Q
过直线上一点作这条直线的垂线就是作以这点为顶点的平角的角平分线.
经过一点可用直尺和圆规作一条直线与已知直线垂直.
新知应用
1. (1)用直尺和圆规把图①中把∠MON四等分;
O
M
N
①
新知应用
(2)用直尺和圆规在图②中过点B作BC的垂线,并指出所作图中∠ABC的余角.
B
C
A
②
M
N
P
∠ABC的余角是∠ABP.
新知应用
2. 用直尺和圆规作一个直角三角形,使它的两条直角边分别等于a、b.
解:如上图,△AOB为所求作的直角三角形.
O
C
D
a
b
b
a
A
B
课堂小结
作已知角的角平分线
过直线上的一点作已知直线的垂线
过直线外的一点作已知直线的垂线
特例
经过一点可用直尺和圆规作一条直线与已知直线垂直.
作图依据:SSS
当堂检测
1.已知∠AOB,求作射线OC,使OC平分∠AOB.
①画射线OC即为所求;
②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
则上面作法的合理顺序为( ).
A.②③① B.③①② C.③②① D.②①③
A
当堂检测
2. 小米在用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D、E为圆心,大于 DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
①②③④ B. ④③②①
C. ②④③① D. ④③①②
D
当堂检测
3.如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD.以下说法错误的是( )
A
B
C
D
E
O
A.△OCD是等腰三角形
B.点E到OA、OB的距离相等
C.CD垂直平分OE
D.证明射线OE是角平分线的依据是SSS
C
当堂检测
4.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图正确的是( )
B
当堂检测
5.已知△ABC,利用尺规作图,作BC边上的高AD,正确的是( )
B
当堂检测
6.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A
A. B. C. D.
当堂检测
9.
7.如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是( )
A. DB=DE
B. AB=AE
C. ∠EDC=∠BAC
D. ∠DAC=∠C
D
8.作一个角的平分线的尺规作图的理论依据是__________.
当堂检测
9.如图,依据尺规作图的痕迹,计算∠α= °.
SSS
34
当堂检测
10.如图,一块余料ABCD,AD∥BC,现进行如下操作以点B为圆心,适当长为半径作圆弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH的长为半径作圆弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.连结OG、OH.若∠A=124°,则∠AEB的大小是______度.
28
当堂检测
11.在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是___________
图①与图③
当堂检测
12.如图,已知△ABC.
(1)用直尺和圆规作出△ABC的角平分线CD;(不写作法,但保留作图痕迹)
(2)过点D画出△ACD的高DE和△BCD的高DF;
(3)量出DE、DF的长度,你有怎样的发现
把你的发现用文字语言表达出来.
A
B
C
当堂检测
解:(1)△ABC的角平分线AD如图所示.
(2)线段DE,DF如图所示.
(3)测量发现:DE=DF.
用文字语言表述如下:角平分线上的点到角两边的距离相等.
A
B
C
D
E
F
新知应用
12. (4)如图,点M和点N在∠AOB内部.
请你根据上面结论作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);
A
O
C
M
N
P
解:(4)如图,作∠AOB的角平分线与线段MN的垂直平分线交于P点,即点到点和点的距离相等,且到两边的距离也相等;
第1章 · 全等三角形
1.3 探索三角形全等的条件
第7课时 用圆规、直尺作角平分线及过已知点作已知直线的垂线
学习目标
会用直尺和圆规作角平分线以及过已知直线外一点作这条直线的垂线, 并能说出作图的依据.
知识回顾
1.什么是角的平分线
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.
A
B
O
C
知识回顾
2.你能找出一个角的平分线吗?
方法一:对折
方法二:用量角器
如果在黑板、墙壁呢?
如果画22.5°的角平分线,测量11.25°时,是不是不够精确呢?
怎样更精确地平分
一个角呢?
新知探索
工人师傅常用角尺平分一个角.
如图,在∠AOB的两边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,这时过角尺顶点C连OC,射线OC就是∠AOB的平分线.
你能说明这样画角平分线的道理吗?
数学来源于生活,古代的能工巧匠就找到了解决的办法.
解:由题意得:MC=NC.
在△OMC和△ONC中,
∴△OMC≌△ONC(SSS).
新知探索
∴∠MOC=∠NOC.
∴OC平分∠AOB.
按照上面的工人师傅的操作过程,你能利用直尺和圆规,画出∠AOB的平分线吗?请你试一试.
新知探索
已知:∠AOB.
求作:∠AOB的平分线.
A
B
M
N
C
O
作法:
1.以____为圆心,________为半径作弧,分别交射线OA、OB于点M、N;
O
任意长
2.分别点以_______为圆心,________的长为半径作弧,两弧在∠AOB的内部交于点___.
M、N
大于MN
C
3.作射线______.
OC
OC就是∠AOB的平分线.
新知探索
A
B
M
N
C
O
E
1.从图中你还能发现哪些结论?
2.OC⊥MN吗?
由此,你能找到用直尺和圆规过已知直线外一点作这条直线的垂线的方法了吗?
新知探索
A
B
P
C
D
Q
作法:
3.作直线PQ.
1.以点P为圆心,适当的长为半径作弧,使它与直线AB交于C、D.
直线PQ就是经过直线AB外一点P的AB的垂线.
2.分别以点C、D为圆心,大于CD的长为半径作弧,两弧交于点Q.
若点P在直线上呢?
新知探索
A
B
P
C
D
作法:
3.作直线PQ.
1.以点P为圆心,适当的长为半径作弧,使它与直线AB交于C、D.
直线PQ就是经过直线AB上一点P的AB的垂线.
2.分别以点C、D为圆心,大于CD的长为半径作弧,两弧交于点Q.
Q
过直线上一点作这条直线的垂线就是作以这点为顶点的平角的角平分线.
经过一点可用直尺和圆规作一条直线与已知直线垂直.
新知应用
1. (1)用直尺和圆规把图①中把∠MON四等分;
O
M
N
①
新知应用
(2)用直尺和圆规在图②中过点B作BC的垂线,并指出所作图中∠ABC的余角.
B
C
A
②
M
N
P
∠ABC的余角是∠ABP.
新知应用
2. 用直尺和圆规作一个直角三角形,使它的两条直角边分别等于a、b.
解:如上图,△AOB为所求作的直角三角形.
O
C
D
a
b
b
a
A
B
课堂小结
作已知角的角平分线
过直线上的一点作已知直线的垂线
过直线外的一点作已知直线的垂线
特例
经过一点可用直尺和圆规作一条直线与已知直线垂直.
作图依据:SSS
当堂检测
1.已知∠AOB,求作射线OC,使OC平分∠AOB.
①画射线OC即为所求;
②以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;③分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
则上面作法的合理顺序为( ).
A.②③① B.③①② C.③②① D.②①③
A
当堂检测
2. 小米在用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D、E为圆心,大于 DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.
其中顺序正确的作图步骤是( )
①②③④ B. ④③②①
C. ②④③① D. ④③①②
D
当堂检测
3.如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD.以下说法错误的是( )
A
B
C
D
E
O
A.△OCD是等腰三角形
B.点E到OA、OB的距离相等
C.CD垂直平分OE
D.证明射线OE是角平分线的依据是SSS
C
当堂检测
4.尺规作图:经过已知直线外一点作这条直线的垂线,下列作图正确的是( )
B
当堂检测
5.已知△ABC,利用尺规作图,作BC边上的高AD,正确的是( )
B
当堂检测
6.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A
A. B. C. D.
当堂检测
9.
7.如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是( )
A. DB=DE
B. AB=AE
C. ∠EDC=∠BAC
D. ∠DAC=∠C
D
8.作一个角的平分线的尺规作图的理论依据是__________.
当堂检测
9.如图,依据尺规作图的痕迹,计算∠α= °.
SSS
34
当堂检测
10.如图,一块余料ABCD,AD∥BC,现进行如下操作以点B为圆心,适当长为半径作圆弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH的长为半径作圆弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.连结OG、OH.若∠A=124°,则∠AEB的大小是______度.
28
当堂检测
11.在以下三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是___________
图①与图③
当堂检测
12.如图,已知△ABC.
(1)用直尺和圆规作出△ABC的角平分线CD;(不写作法,但保留作图痕迹)
(2)过点D画出△ACD的高DE和△BCD的高DF;
(3)量出DE、DF的长度,你有怎样的发现
把你的发现用文字语言表达出来.
A
B
C
当堂检测
解:(1)△ABC的角平分线AD如图所示.
(2)线段DE,DF如图所示.
(3)测量发现:DE=DF.
用文字语言表述如下:角平分线上的点到角两边的距离相等.
A
B
C
D
E
F
新知应用
12. (4)如图,点M和点N在∠AOB内部.
请你根据上面结论作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);
A
O
C
M
N
P
解:(4)如图,作∠AOB的角平分线与线段MN的垂直平分线交于P点,即点到点和点的距离相等,且到两边的距离也相等;
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
