第一章 特殊四边形 单元复习课件(34张PPT)
文档属性
| 名称 | 第一章 特殊四边形 单元复习课件(34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
章末讲义
第一章 特殊平行四边形
菱形的概念:有一组邻边相等的平行四边形叫做菱形。
【注意事项】
1、菱形是一种特殊的平行四边形。
2、平行四边形不一定是菱形。
【菱形的条件】①平行四边形;②一组邻边相等。
平行四边形
菱形
矩形的概念:有一个角是直角的平行四边形叫做矩形,也叫做长方形.
【注意】
1)矩形是一种特殊的平行四边形。
2)平行四边形不一定是矩形。
【矩形的条件】①平行四边形;②其中有一个角是直角。
A
B
D
C
平行四边形
菱形
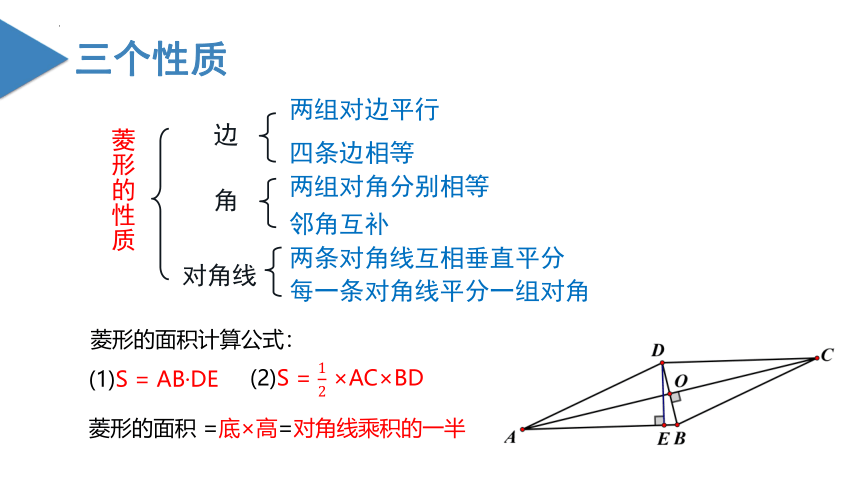
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
边
角
对角线
两条对角线互相垂直平分
每一条对角线平分一组对角
(1)S = AB·DE
菱形的面积计算公式:
菱形的面积 =底×高=对角线乘积的一半
(2)S = ×AC×BD
矩形的性质
两组对边平行
两组对边相等
四个角是直角
邻角互补
边
角
对角线
两条对角线互相平分
两条对角线相等
1)四个角都是直角
2)四条边都相等
3)对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形。
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。所以矩形、菱形有的性质,正方形都有。
正方形与平行四边形、矩形、菱形的关系
有一组邻边相等的平行四边形叫做菱形。
对角线互相垂直的平行四边形是菱形。
四条边相等的四边形是菱形。
菱形的判定方法
(1)定义法:
(2)判定定理1:
(3)判定定理2:
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定
定义法:
定理:
定理1:
定理2:
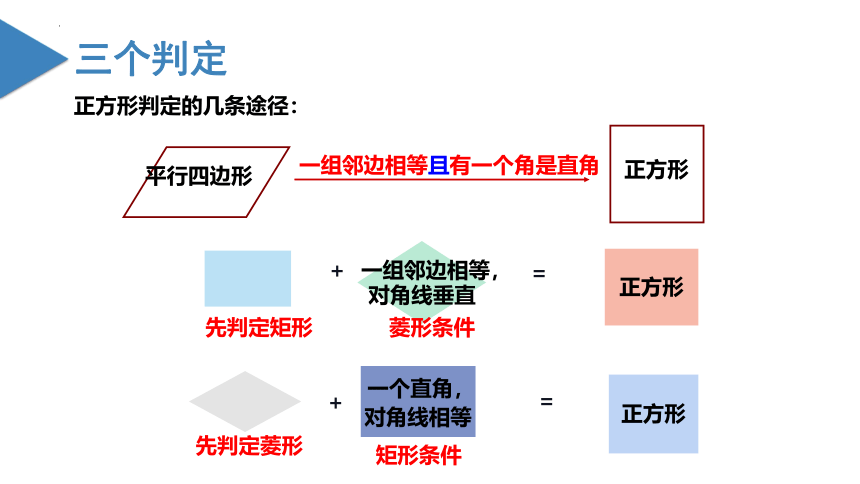
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件
菱形条件
一个直角,
一组邻边相等,
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等且有一个角是直角
=
=
有关菱形问题方法总结:
1.面积求法:两种。
2.边、线求法:利用4个直角三角形,知二求一。
3.角:知一角而知全部。
4.关注30°、60°、120°的特殊性。
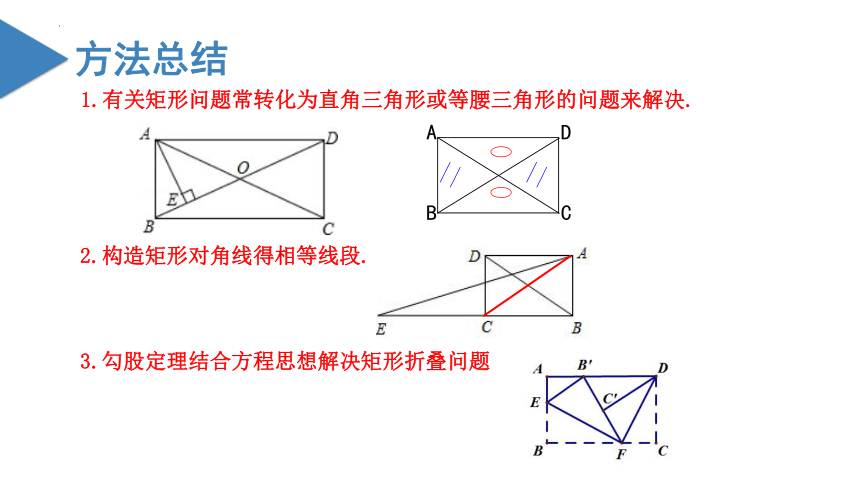
1.有关矩形问题常转化为直角三角形或等腰三角形的问题来解决.
2.构造矩形对角线得相等线段.
3.勾股定理结合方程思想解决矩形折叠问题
D
B
C
A
中点四边形的概念:依次连接任意一个四边形各边中点所得的四边形叫做中点四边形。
中点四边形的性质:
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
①四边形EFGH是平行四边形 ②CEFGH =AC+BD ③sEFGH =sABCD
结论一:顺次连接任意四边形各边中点所组成的四边形是平行四边形。
结论二:中点四边形的周长等于原四边形对角线之和。
结论三:中点四边形的面积等于原四边形面积的一半。
结论四:顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形。
结论五:顺次连接对角线相等的四边形各边中点所组成的四边形是菱形。
结论六:顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形。
速记口诀:矩中菱,菱中矩,正中正。
例1.平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线互相垂直平分
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别相等 B.两组对边分别平行
C.两条对角线相等 D.两条对角线互相垂直
2.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
3.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
例2.在菱形ABCD中,若∠B+∠D=160°,则∠C= °.
例3.菱形的边长为5,则它的周长为 .
【详解】解:在菱形ABCD中,∠D=∠B,
∵∠B+∠D=160°,∴∠D=∠B=80°.
在菱形ABCD中,AB∥CD,∴∠B+∠C=180°,
∴∠C=180°﹣80°=100°.故答案是:100.
【详解】∵菱形的四条边相等.∴周长:,
故答案为:20.
1.如图,菱形中,已知,则的大小是 .
2.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
【详解】解:∵菱形中,,
∴
∴故答案为:.
【详解】解:∵四边形ABCD是菱形,∴BO=DO,AC⊥DB,AO=CO,
∵BD=2cm,∴BO=1cm,
∵AB=cm,∴AO===2(cm),
∴AC=2AO=4cm.
∴S菱形ABCD=(cm2).故答案为:4.
3.菱形的两条对角线长分别为5和8,则这个菱形的面积为 .
如图,四边形是菱形,,于点H,则 .
5. 如上图,菱形的对角线,相交于点,已知,菱形的面积为24,则的长为 .
【详解】解:∵四边形是菱形,,
∴,,
∴在中,,
∴,
∴,故答案为:.
【详解】解:∵四边形ABCD为菱形;
∴AC=2OA=8,,
∴,∴BD=6,故答案为:6
例4.如图,在 ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,
求证: ABCD是菱形.
【详解】证明:∵AE⊥BC于点E,CF⊥AB于点F,
∴∠CFB=∠AEB=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴BC=BA
∵四边形ABCD是平行四边形,
∴ ABCD是菱形.
1.如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
【详解】解:证明:(1)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,EH是△ADC的中位线,
∴EG=AB,EH=CD,
∵AB=CD,
∴EG=EH;
1.如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
(2)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG∥AB,HF∥AB,EH∥CD,FE∥DC,
∴GF∥EH,GE∥FH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形,
∵四边形ABCD中,点E、F、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,GF是△BCD的中位线,
∴GE=AB,GF=CD,
∵AB=CD,∴GE=GF,∴四边形EHFG是菱形.
例5.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
【详解】解:∵MN是AC的垂直平分线,∴EC=EA ∴∠ECA=∠EAC,
∵四边形ABCD是矩形,∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°-70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
故答案为:40.
例6.如图,在矩形中,对角线,相交于点,点是边的中点,点在对角线上,且,连接.若,则 .
【详解】∵四边形ABCD是矩形,
∴BD=AC=10,OA=AC,OD=BD=5,
∵,
∴,即点F是OA的中点.
∵点是边的中点,
∴EF是△AOD的中位线,
∴.
故答案为:.
1.“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF,分别架在墙体的点,处,且,侧面四边形为矩形,若测得,则 .
【详解】四边形为矩形
,
故答案为:.
2.如图,是矩形的对角线的中点,是的中点.若,,则四边形的周长为 .
【详解】解:,,
,,,
点和点分别是和的中点,
OB=6.5,,是的中位线,
OM=CD/2=2.5
.
故答案为:20.
3.如图,在矩形ABCD中,对角线AC,BD相交于O,EF过点O分别交AB,CD于E,F,已知AB=8cm,AD=5cm,那么图中阴影部分面积为 cm2.
例7.如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
【详解】解:由折叠性质可得CF=BC=5,BE=EF,
由矩形性质有CD=AB=3,BC=AD=5,
∵∠D=90°,∴,
所以,
所以 BE=EF=x,则AE=AB-BE=3-x,在直角三角形AEF中:
,∴,解得,
∴,
故答案为:.
1.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将DAE沿DE折叠,使点A落在对角线BD上的点处,则AE的长为 .
【详解】∵AB=12,BC=5,∴AD=5,∴,
根据折叠可得:AD=A′D=5,∴A′B=13-5=8,
设AE=x,则A′E=x,BE=12-x,
在Rt△A′EB中:,
解得:.
故答案为:
2.如图,将矩形沿着对角线折叠,使点落在处,交于,若,, .
【详解】解:由折叠可知,∠CBD=∠EBD,
,,∠EBD=∠EDB,BE=DE,
,.
设,则,,
在中,由勾股定理得:
即,解得:,
.,
故答案为:.
例8.如图,在中,AC=BC,M、N分别是AB和CD的中点.
(1)求证:四边形AMCN是矩形;
(2)若∠B=60°,BC=8,求的面积.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵M、N分别是AB和CD的中点,
∴AM=BM,AM∥CN,AM=CN,
∴四边形AMCN是平行四边形,
又∵AC=BC,AM=BM,
∴CM⊥AB,
∴∠CMA=90°,
∴四边形AMCN是矩形;
(2)解:∵∠B=60°,BC=8,∠BMC=90°,
∴∠BCM=30°,
∴Rt△BCM中,BM=BC=4,CM=4,
∵AC=BC,CM⊥AB,
∴AB=2BM=8,
∴的面积为AB×CM=8×4=32.
1.如图,菱形ABCD的对角线AC、BD相交于点O,,,OE与AB交于点F.
(1)求证:四边形AEBO为矩形;
(2)若OE=10,AC=16,求菱形ABCD的面积.
例9.如图,在正方形ABCD中,E是AD上一点,连接CE,交BD于点F,若AB=BF,则∠AEF= °.
【详解】∵四边形ABCD为正方形,
∴AB=BC,ADBC,∠ABD=∠CBD=45°,
∵AB=BF,
∴BF=BC,
∴∠BFC=∠BCF=67.5°,
∵ADBC,
∴∠BCF=∠DEF=67.5°,
∴∠AEF=180°﹣∠DEF=112.5°.
故答案为:112.5.
1.一个正方形的对角线长为2,则其面积为 .
2.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,点D的坐标是(2,3),则点B的坐标是 .
【详解】解:∵D的坐标是(2,3),B、C在x轴上,
∴DC=3,OC=2,
∵四边形ABCD是正方形,
∴BC=CD=3,
∴OB=3-2=1,
∵B在x轴的负半轴上,
∴B (-1,0).
故答案为: (-1,0) .
例10.如图,已知点,,,H分别是正方形四条边上的点,并且.
求证:四边形EFGH是正方形.
1.已知:如图,在矩形ABCD中,E、F分别是边CD、AD上的点,,且.求证:矩形ABCD是正方形.
章末讲义
第一章 特殊平行四边形
菱形的概念:有一组邻边相等的平行四边形叫做菱形。
【注意事项】
1、菱形是一种特殊的平行四边形。
2、平行四边形不一定是菱形。
【菱形的条件】①平行四边形;②一组邻边相等。
平行四边形
菱形
矩形的概念:有一个角是直角的平行四边形叫做矩形,也叫做长方形.
【注意】
1)矩形是一种特殊的平行四边形。
2)平行四边形不一定是矩形。
【矩形的条件】①平行四边形;②其中有一个角是直角。
A
B
D
C
平行四边形
菱形
菱形的性质
两组对边平行
四条边相等
两组对角分别相等
邻角互补
边
角
对角线
两条对角线互相垂直平分
每一条对角线平分一组对角
(1)S = AB·DE
菱形的面积计算公式:
菱形的面积 =底×高=对角线乘积的一半
(2)S = ×AC×BD
矩形的性质
两组对边平行
两组对边相等
四个角是直角
邻角互补
边
角
对角线
两条对角线互相平分
两条对角线相等
1)四个角都是直角
2)四条边都相等
3)对角线相等且互相垂直平分
正方形的性质
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形。
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。所以矩形、菱形有的性质,正方形都有。
正方形与平行四边形、矩形、菱形的关系
有一组邻边相等的平行四边形叫做菱形。
对角线互相垂直的平行四边形是菱形。
四条边相等的四边形是菱形。
菱形的判定方法
(1)定义法:
(2)判定定理1:
(3)判定定理2:
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定
定义法:
定理:
定理1:
定理2:
正方形判定的几条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件
菱形条件
一个直角,
一组邻边相等,
对角线相等
对角线垂直
平行四边形
正方形
一组邻边相等且有一个角是直角
=
=
有关菱形问题方法总结:
1.面积求法:两种。
2.边、线求法:利用4个直角三角形,知二求一。
3.角:知一角而知全部。
4.关注30°、60°、120°的特殊性。
1.有关矩形问题常转化为直角三角形或等腰三角形的问题来解决.
2.构造矩形对角线得相等线段.
3.勾股定理结合方程思想解决矩形折叠问题
D
B
C
A
中点四边形的概念:依次连接任意一个四边形各边中点所得的四边形叫做中点四边形。
中点四边形的性质:
已知点E、F、G、H分别为四边形ABCD四条边AB、BC、CD、AD的中点,则
①四边形EFGH是平行四边形 ②CEFGH =AC+BD ③sEFGH =sABCD
结论一:顺次连接任意四边形各边中点所组成的四边形是平行四边形。
结论二:中点四边形的周长等于原四边形对角线之和。
结论三:中点四边形的面积等于原四边形面积的一半。
结论四:顺次连接对角线互相垂直的四边形各边中点所组成的四边形是矩形。
结论五:顺次连接对角线相等的四边形各边中点所组成的四边形是菱形。
结论六:顺次连接对角线互相垂直且相等的四边形各边中点所组成的四边形是正方形。
速记口诀:矩中菱,菱中矩,正中正。
例1.平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.对角线互相垂直平分
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别相等 B.两组对边分别平行
C.两条对角线相等 D.两条对角线互相垂直
2.下列关系中,是菱形的性质但不是平行四边形的性质的是( )
A.对角线垂直 B.两组对边分别平行
C.对角线互相平分 D.两组对角分别相等
3.正方形具有而矩形不一定具有的性质是( )
A.四个角都相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
例2.在菱形ABCD中,若∠B+∠D=160°,则∠C= °.
例3.菱形的边长为5,则它的周长为 .
【详解】解:在菱形ABCD中,∠D=∠B,
∵∠B+∠D=160°,∴∠D=∠B=80°.
在菱形ABCD中,AB∥CD,∴∠B+∠C=180°,
∴∠C=180°﹣80°=100°.故答案是:100.
【详解】∵菱形的四条边相等.∴周长:,
故答案为:20.
1.如图,菱形中,已知,则的大小是 .
2.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
【详解】解:∵菱形中,,
∴
∴故答案为:.
【详解】解:∵四边形ABCD是菱形,∴BO=DO,AC⊥DB,AO=CO,
∵BD=2cm,∴BO=1cm,
∵AB=cm,∴AO===2(cm),
∴AC=2AO=4cm.
∴S菱形ABCD=(cm2).故答案为:4.
3.菱形的两条对角线长分别为5和8,则这个菱形的面积为 .
如图,四边形是菱形,,于点H,则 .
5. 如上图,菱形的对角线,相交于点,已知,菱形的面积为24,则的长为 .
【详解】解:∵四边形是菱形,,
∴,,
∴在中,,
∴,
∴,故答案为:.
【详解】解:∵四边形ABCD为菱形;
∴AC=2OA=8,,
∴,∴BD=6,故答案为:6
例4.如图,在 ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,
求证: ABCD是菱形.
【详解】证明:∵AE⊥BC于点E,CF⊥AB于点F,
∴∠CFB=∠AEB=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴BC=BA
∵四边形ABCD是平行四边形,
∴ ABCD是菱形.
1.如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
【详解】解:证明:(1)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,EH是△ADC的中位线,
∴EG=AB,EH=CD,
∵AB=CD,
∴EG=EH;
1.如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
(2)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG∥AB,HF∥AB,EH∥CD,FE∥DC,
∴GF∥EH,GE∥FH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形,
∵四边形ABCD中,点E、F、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,GF是△BCD的中位线,
∴GE=AB,GF=CD,
∵AB=CD,∴GE=GF,∴四边形EHFG是菱形.
例5.如图,矩形ABCD中,AC的垂直平分线MN与AB交于点E,连接CE.若∠CAD=70°,则∠DCE= °.
【详解】解:∵MN是AC的垂直平分线,∴EC=EA ∴∠ECA=∠EAC,
∵四边形ABCD是矩形,∴AB∥CD,∠D=90°,
∴∠DCA=∠EAC=90°-70°=20°,
∴∠DCE=∠DCA+∠ECA=20°+20°=40°,
故答案为:40.
例6.如图,在矩形中,对角线,相交于点,点是边的中点,点在对角线上,且,连接.若,则 .
【详解】∵四边形ABCD是矩形,
∴BD=AC=10,OA=AC,OD=BD=5,
∵,
∴,即点F是OA的中点.
∵点是边的中点,
∴EF是△AOD的中位线,
∴.
故答案为:.
1.“美丽乡村”建设使我市农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF,分别架在墙体的点,处,且,侧面四边形为矩形,若测得,则 .
【详解】四边形为矩形
,
故答案为:.
2.如图,是矩形的对角线的中点,是的中点.若,,则四边形的周长为 .
【详解】解:,,
,,,
点和点分别是和的中点,
OB=6.5,,是的中位线,
OM=CD/2=2.5
.
故答案为:20.
3.如图,在矩形ABCD中,对角线AC,BD相交于O,EF过点O分别交AB,CD于E,F,已知AB=8cm,AD=5cm,那么图中阴影部分面积为 cm2.
例7.如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
【详解】解:由折叠性质可得CF=BC=5,BE=EF,
由矩形性质有CD=AB=3,BC=AD=5,
∵∠D=90°,∴,
所以,
所以 BE=EF=x,则AE=AB-BE=3-x,在直角三角形AEF中:
,∴,解得,
∴,
故答案为:.
1.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将DAE沿DE折叠,使点A落在对角线BD上的点处,则AE的长为 .
【详解】∵AB=12,BC=5,∴AD=5,∴,
根据折叠可得:AD=A′D=5,∴A′B=13-5=8,
设AE=x,则A′E=x,BE=12-x,
在Rt△A′EB中:,
解得:.
故答案为:
2.如图,将矩形沿着对角线折叠,使点落在处,交于,若,, .
【详解】解:由折叠可知,∠CBD=∠EBD,
,,∠EBD=∠EDB,BE=DE,
,.
设,则,,
在中,由勾股定理得:
即,解得:,
.,
故答案为:.
例8.如图,在中,AC=BC,M、N分别是AB和CD的中点.
(1)求证:四边形AMCN是矩形;
(2)若∠B=60°,BC=8,求的面积.
【详解】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵M、N分别是AB和CD的中点,
∴AM=BM,AM∥CN,AM=CN,
∴四边形AMCN是平行四边形,
又∵AC=BC,AM=BM,
∴CM⊥AB,
∴∠CMA=90°,
∴四边形AMCN是矩形;
(2)解:∵∠B=60°,BC=8,∠BMC=90°,
∴∠BCM=30°,
∴Rt△BCM中,BM=BC=4,CM=4,
∵AC=BC,CM⊥AB,
∴AB=2BM=8,
∴的面积为AB×CM=8×4=32.
1.如图,菱形ABCD的对角线AC、BD相交于点O,,,OE与AB交于点F.
(1)求证:四边形AEBO为矩形;
(2)若OE=10,AC=16,求菱形ABCD的面积.
例9.如图,在正方形ABCD中,E是AD上一点,连接CE,交BD于点F,若AB=BF,则∠AEF= °.
【详解】∵四边形ABCD为正方形,
∴AB=BC,ADBC,∠ABD=∠CBD=45°,
∵AB=BF,
∴BF=BC,
∴∠BFC=∠BCF=67.5°,
∵ADBC,
∴∠BCF=∠DEF=67.5°,
∴∠AEF=180°﹣∠DEF=112.5°.
故答案为:112.5.
1.一个正方形的对角线长为2,则其面积为 .
2.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,点D的坐标是(2,3),则点B的坐标是 .
【详解】解:∵D的坐标是(2,3),B、C在x轴上,
∴DC=3,OC=2,
∵四边形ABCD是正方形,
∴BC=CD=3,
∴OB=3-2=1,
∵B在x轴的负半轴上,
∴B (-1,0).
故答案为: (-1,0) .
例10.如图,已知点,,,H分别是正方形四条边上的点,并且.
求证:四边形EFGH是正方形.
1.已知:如图,在矩形ABCD中,E、F分别是边CD、AD上的点,,且.求证:矩形ABCD是正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
