13.2 画轴对称图形 导学案(含答案)
文档属性
| 名称 | 13.2 画轴对称图形 导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-14 00:00:00 | ||
图片预览


文档简介
13.2 画轴对称图形
学习目标
1.能够按要求作出简单平面图形经过一次对称后的图形.
2. 理解与已知点关于x轴或y轴对称的点的坐标的变化规律.
3. 在找点、绘图的过程中体会数形结合的思想,增强解决问题的信心
学习策略
1.通过动手操作领会轴对称图形的作法;
2.牢记轴对称图形的作图方法,关于坐标轴的对称的点的规律
学习过程
一.复习回顾:
1.什么叫线段的垂直平分线?线段垂直平分线的性质?
2.尺规作图:线段的垂直平分线步骤
二.新课学习:
知识点一:画轴对称图形
阅读课本本课时的内容,解决下列问题.
1.将一张纸对折,然后稍用劲在纸上画一个三角形,将纸打开,根据痕迹在折痕的另一侧画出另一个三角形,则这两个三角形关于折痕 ,这两个三角形是 三角形.
【答案】对称;全等
2.连接上述两个三角形的对应点,可以发现它们到折痕的距离 ,并且连线 于折痕,所以连接任意一对对应点的线段都被对称轴 .
【答案】相等;垂直;垂直平分
3.由课本“例1”可知:
(1)△ABC关于直线的对称图形是什么形状
【答案】三角形
(2)△ABC的轴对称图形可以由哪几个点确定
【答案】三角形的三个顶点
(3)在△ABC上,取哪几个点作出其关于的对称点
【答案】A、B、C
4.如何作一个已知点关于直线的对称点
(1)过已知点作对称轴的 ;
(2)在对称轴的另一侧延长垂线段,使延长后的部分 所作的垂线段;
(3)延长后得到的线段的另一端点即为求作的对称点.
总结:(1)由一个平面图形可以得到它关于一条直线成轴对称的图形,这个图形与原图形的形状、大小 .新图形上每个点都是原图形上的某一点关于直线的 .连接任意一对对应点的线段都被对称轴 .
(2)画已知图形关于某直线对称的图形的方法.
①确定原图形中的 (一般为端点或顶点);②画出关键点关于直线的 ;③连接所求作的对称点,所得图形就是求作的图形.
【答案】垂线段;等
知识点二:坐标系内点的对称规律
1.课本“思考”中的西直门的坐标可以表示为 ,与东直门的坐标比较,横坐标 ,纵坐标 .由轴对称的定义,我们可以说西直门和东直门关于 轴对称.
【答案】(-3.5,4);互为相反数;相等;y
2.在坐标系中描出下列各点:A(2,-1)、B(3,2)、C(2,1)、D(-3,2).
观察这些点在坐标系中的位置,可以发现:点 与点 关于x轴对称,点 和点 关于y轴对称.
综之:点(x,y)关于x轴对称的点的坐标为 ,即横坐标 ,纵坐标 ;点(x,y)关于y轴对称的点的坐标为 ,即横坐标 ,纵坐标 .
【答案】A;C;B;D;(x,-y);相等;互为相反数;(-x,y);互为相反数;相等
知识点三:坐标系内轴对称图形的作法
要作一个△ABC关于x(或y)轴的对称三角形,只要分别作出 、 、 关于x(或y)轴对称的点A'、B'、C',连接A'B'、B'C'、C'A', 即为要求作的三角形.
总结:在坐标系内作一个图形关于坐标轴的对称图形,只要先求出已知图形中的一些 (如多边形的 )的对称点的坐标.描出并 这些点,就可以得到这个图形关于坐标轴 的图形.
【答案】点A;点B;点C;△A'B'C';特殊点;顶点;连接;对称
三.尝试应用:
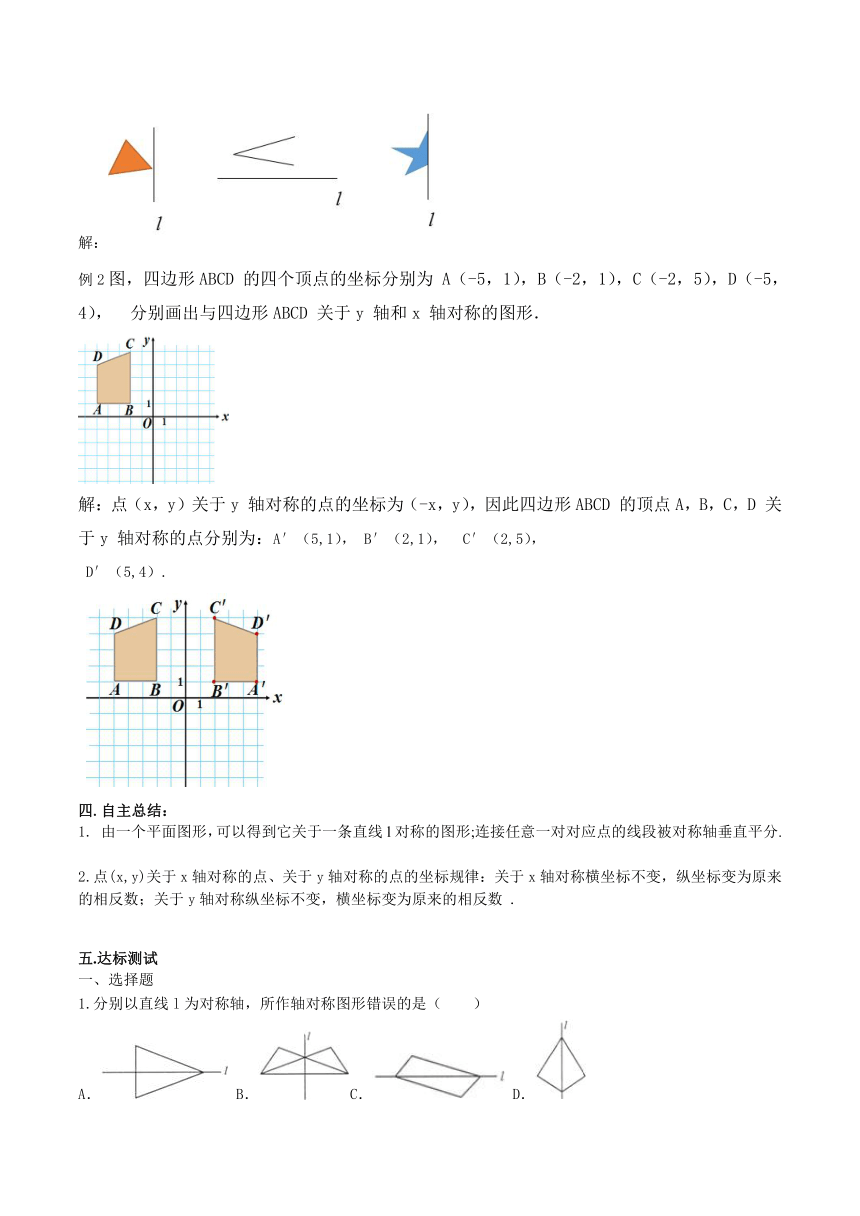
例1 如图,把下列图形补成关于直线l对称的图形.
解:
例2图,四边形ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4), 分别画出与四边形ABCD 关于y 轴和x 轴对称的图形.
解:点(x,y)关于y 轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,D 关于y 轴对称的点分别为:A′(5,1), B′(2,1), C′(2,5),
D′(5,4).
四.自主总结:
1. 由一个平面图形,可以得到它关于一条直线l对称的图形;连接任意一对对应点的线段被对称轴垂直平分.
2.点(x,y)关于x轴对称的点、关于y轴对称的点的坐标规律:关于x轴对称横坐标不变,纵坐标变为原来的相反数;关于y轴对称纵坐标不变,横坐标变为原来的相反数 .
五.达标测试
一、选择题
1.分别以直线l为对称轴,所作轴对称图形错误的是( )
A. B.C. D.
2.平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )
A.(-2,-3) B.(2,-3) C.(-3,-2) D.(3,-2)
3. 已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(-3,2) B.(3,2) C.(-3,-2) D.(3,-2)
4. 若点A(m,2)与点B(3,n)关于x轴对称, 则m+n的值是( A )
A.1 B.-2 C.2 D.5
若点A(m,2)与点B(3,n)关于x轴对称,则m+n的值是( )
A.1 B.﹣2 C.2 D.5
5. 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,则田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.3个 C.2个 D.4个
二、填空题
6. 作已知点关于某直线的对称点的第一步是( )
7.正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有 种.
8. 平面直角坐标系中的点P(2 m,m)关于x轴的对称点在第四象限,则m的取值范围为________.
三、解答题
9. 如图,画△ABC关于直线m的对称图形.
10. 在平面直角坐标系中,已知点P(2a+3,3),Q(-4,b-2),根据下列条件求a,b值.
(1)点P,Q关于x轴对称;
(2)P,Q两点关于y轴对称;
(3)直线PQ∥x轴;
(4)直线PQ∥y轴.
参考答案
1.C
2.A
3. B
4. A解析:A(m,2)与点B(3,n)关于x轴对称,得
m=3,n=﹣2,m+n=3+(﹣2)=1,故选:A.
5 .B 解析:如图所示:符合题意的有3个三角形.
6. 过已知点作一条直线与已知直线垂直
7. 4解析:如图所示:
,
共4种.
8. 0<m<2 解析:点P(2-m,m)关于x轴对称的点的坐标为P1(2-m,-m),因为P1(2-m,-m)在第四象限,所以,解得0<m<2,所以m的取值范围为 0<m<2.
9. 解:
10. 解:(1)由题意得:2a+3=-4,b-2=-3,解得:a=-,b=-5;(2)由题意得:2a+3=4,b-2=3,解得:a=,b=25;(3)由题意得:2a+3≠-4,b-2=3,解得:a≠-,b=25;(4)由题意得:2a+3=-4,b-2≠3,解得:a=-,b≠25.
学习目标
1.能够按要求作出简单平面图形经过一次对称后的图形.
2. 理解与已知点关于x轴或y轴对称的点的坐标的变化规律.
3. 在找点、绘图的过程中体会数形结合的思想,增强解决问题的信心
学习策略
1.通过动手操作领会轴对称图形的作法;
2.牢记轴对称图形的作图方法,关于坐标轴的对称的点的规律
学习过程
一.复习回顾:
1.什么叫线段的垂直平分线?线段垂直平分线的性质?
2.尺规作图:线段的垂直平分线步骤
二.新课学习:
知识点一:画轴对称图形
阅读课本本课时的内容,解决下列问题.
1.将一张纸对折,然后稍用劲在纸上画一个三角形,将纸打开,根据痕迹在折痕的另一侧画出另一个三角形,则这两个三角形关于折痕 ,这两个三角形是 三角形.
【答案】对称;全等
2.连接上述两个三角形的对应点,可以发现它们到折痕的距离 ,并且连线 于折痕,所以连接任意一对对应点的线段都被对称轴 .
【答案】相等;垂直;垂直平分
3.由课本“例1”可知:
(1)△ABC关于直线的对称图形是什么形状
【答案】三角形
(2)△ABC的轴对称图形可以由哪几个点确定
【答案】三角形的三个顶点
(3)在△ABC上,取哪几个点作出其关于的对称点
【答案】A、B、C
4.如何作一个已知点关于直线的对称点
(1)过已知点作对称轴的 ;
(2)在对称轴的另一侧延长垂线段,使延长后的部分 所作的垂线段;
(3)延长后得到的线段的另一端点即为求作的对称点.
总结:(1)由一个平面图形可以得到它关于一条直线成轴对称的图形,这个图形与原图形的形状、大小 .新图形上每个点都是原图形上的某一点关于直线的 .连接任意一对对应点的线段都被对称轴 .
(2)画已知图形关于某直线对称的图形的方法.
①确定原图形中的 (一般为端点或顶点);②画出关键点关于直线的 ;③连接所求作的对称点,所得图形就是求作的图形.
【答案】垂线段;等
知识点二:坐标系内点的对称规律
1.课本“思考”中的西直门的坐标可以表示为 ,与东直门的坐标比较,横坐标 ,纵坐标 .由轴对称的定义,我们可以说西直门和东直门关于 轴对称.
【答案】(-3.5,4);互为相反数;相等;y
2.在坐标系中描出下列各点:A(2,-1)、B(3,2)、C(2,1)、D(-3,2).
观察这些点在坐标系中的位置,可以发现:点 与点 关于x轴对称,点 和点 关于y轴对称.
综之:点(x,y)关于x轴对称的点的坐标为 ,即横坐标 ,纵坐标 ;点(x,y)关于y轴对称的点的坐标为 ,即横坐标 ,纵坐标 .
【答案】A;C;B;D;(x,-y);相等;互为相反数;(-x,y);互为相反数;相等
知识点三:坐标系内轴对称图形的作法
要作一个△ABC关于x(或y)轴的对称三角形,只要分别作出 、 、 关于x(或y)轴对称的点A'、B'、C',连接A'B'、B'C'、C'A', 即为要求作的三角形.
总结:在坐标系内作一个图形关于坐标轴的对称图形,只要先求出已知图形中的一些 (如多边形的 )的对称点的坐标.描出并 这些点,就可以得到这个图形关于坐标轴 的图形.
【答案】点A;点B;点C;△A'B'C';特殊点;顶点;连接;对称
三.尝试应用:
例1 如图,把下列图形补成关于直线l对称的图形.
解:
例2图,四边形ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4), 分别画出与四边形ABCD 关于y 轴和x 轴对称的图形.
解:点(x,y)关于y 轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,D 关于y 轴对称的点分别为:A′(5,1), B′(2,1), C′(2,5),
D′(5,4).
四.自主总结:
1. 由一个平面图形,可以得到它关于一条直线l对称的图形;连接任意一对对应点的线段被对称轴垂直平分.
2.点(x,y)关于x轴对称的点、关于y轴对称的点的坐标规律:关于x轴对称横坐标不变,纵坐标变为原来的相反数;关于y轴对称纵坐标不变,横坐标变为原来的相反数 .
五.达标测试
一、选择题
1.分别以直线l为对称轴,所作轴对称图形错误的是( )
A. B.C. D.
2.平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )
A.(-2,-3) B.(2,-3) C.(-3,-2) D.(3,-2)
3. 已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是( )
A.(-3,2) B.(3,2) C.(-3,-2) D.(3,-2)
4. 若点A(m,2)与点B(3,n)关于x轴对称, 则m+n的值是( A )
A.1 B.-2 C.2 D.5
若点A(m,2)与点B(3,n)关于x轴对称,则m+n的值是( )
A.1 B.﹣2 C.2 D.5
5. 如图,由4个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,则田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有( )
A.1个 B.3个 C.2个 D.4个
二、填空题
6. 作已知点关于某直线的对称点的第一步是( )
7.正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有 种.
8. 平面直角坐标系中的点P(2 m,m)关于x轴的对称点在第四象限,则m的取值范围为________.
三、解答题
9. 如图,画△ABC关于直线m的对称图形.
10. 在平面直角坐标系中,已知点P(2a+3,3),Q(-4,b-2),根据下列条件求a,b值.
(1)点P,Q关于x轴对称;
(2)P,Q两点关于y轴对称;
(3)直线PQ∥x轴;
(4)直线PQ∥y轴.
参考答案
1.C
2.A
3. B
4. A解析:A(m,2)与点B(3,n)关于x轴对称,得
m=3,n=﹣2,m+n=3+(﹣2)=1,故选:A.
5 .B 解析:如图所示:符合题意的有3个三角形.
6. 过已知点作一条直线与已知直线垂直
7. 4解析:如图所示:
,
共4种.
8. 0<m<2 解析:点P(2-m,m)关于x轴对称的点的坐标为P1(2-m,-m),因为P1(2-m,-m)在第四象限,所以,解得0<m<2,所以m的取值范围为 0<m<2.
9. 解:
10. 解:(1)由题意得:2a+3=-4,b-2=-3,解得:a=-,b=-5;(2)由题意得:2a+3=4,b-2=3,解得:a=,b=25;(3)由题意得:2a+3≠-4,b-2=3,解得:a≠-,b=25;(4)由题意得:2a+3=-4,b-2≠3,解得:a=-,b≠25.
