数学活动课课件[上学期]

课件26张PPT。数学活动动手做
找规律
寻奥秘
通过折叠和观察,归纳出正多面体的顶点
数、面数、棱数之间的关系;
2.通过数学活动,体会平面图形与立体图形的
转换, 发展空间观念;
3.通过自制 “莫比乌斯带”，来感受数学图形的奇妙。
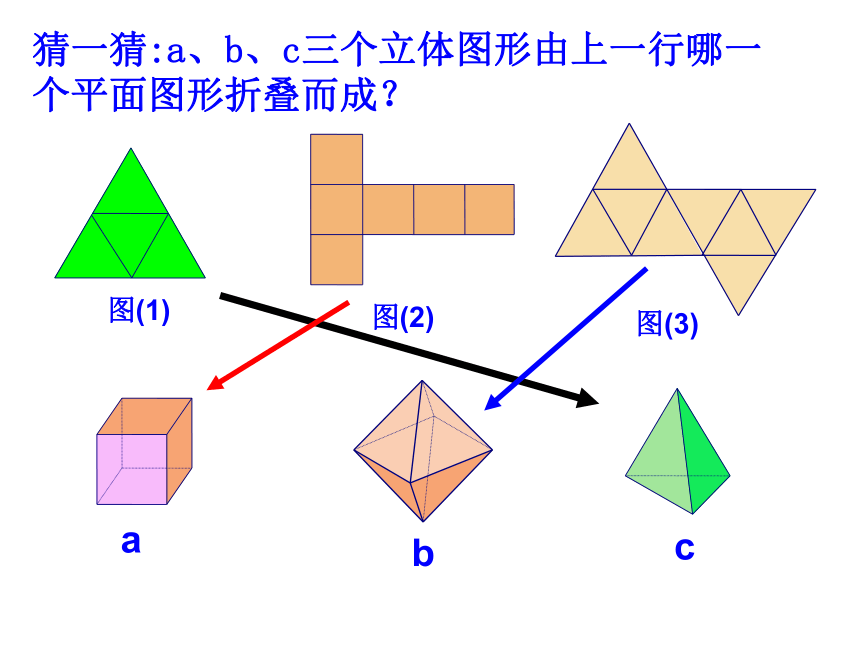
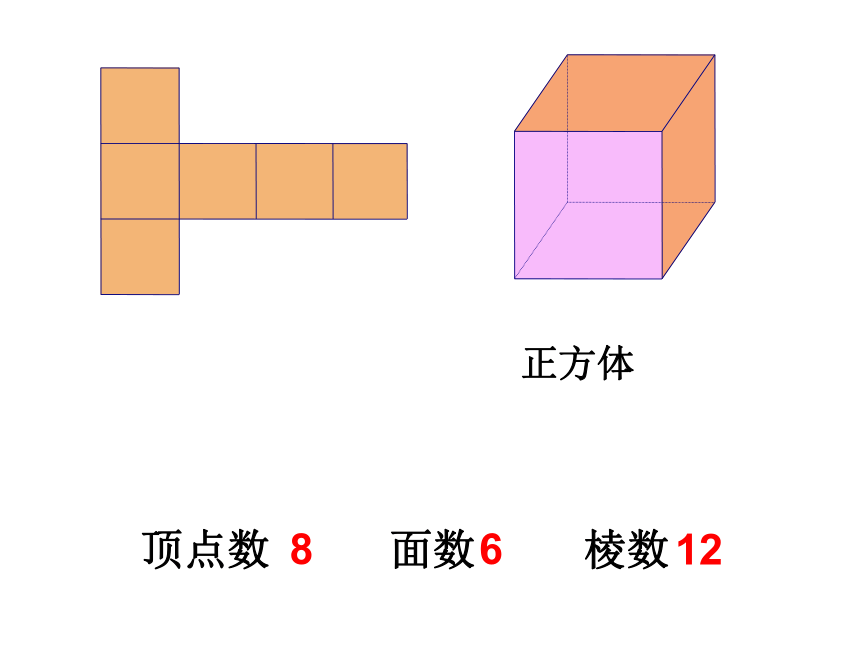
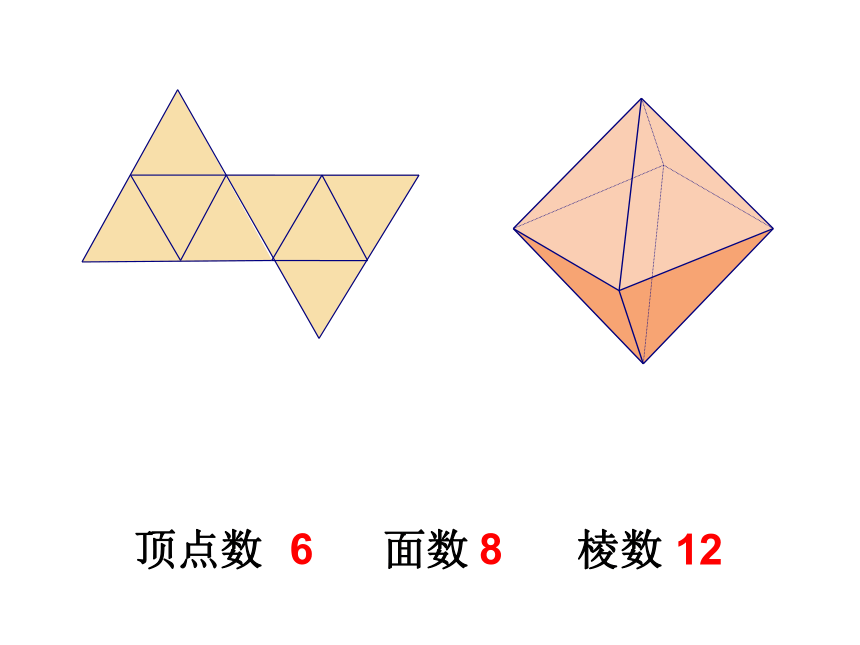
活动目标:猜一猜:a、b、c三个立体图形由上一行哪一个平面图形折叠而成？图(1)图(2)图(3)abc折一折：验证你的判断是否正确?图(1)图(2)图(3)两人小组合作折完的小组尝试填写课本第144页的表格。顶点数 面数 棱数 446正方体顶点数 面数 棱数 8612顶点数 面数 棱数 6812猜一猜：
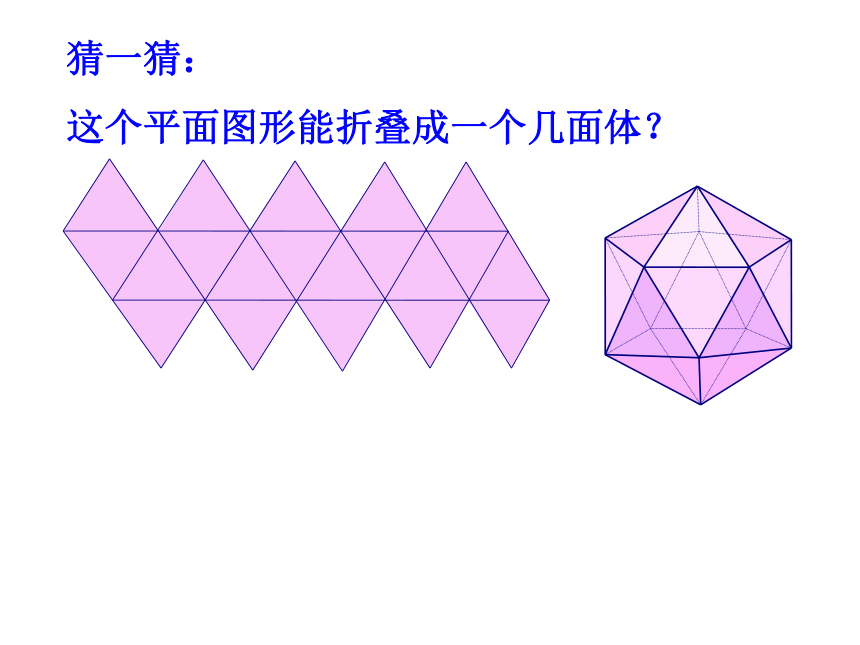
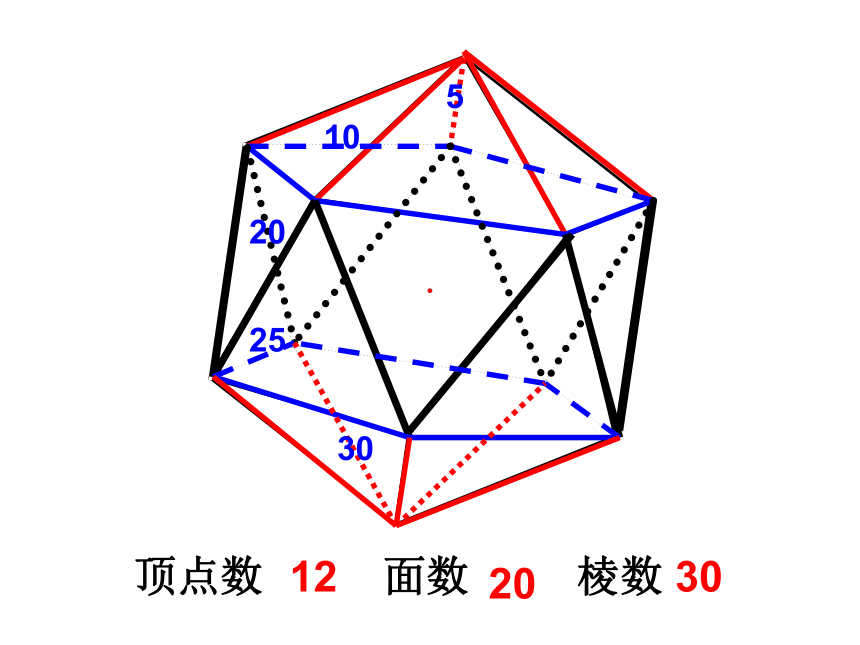
这个平面图形能折叠成一个几面体？510202530顶点数 面数 棱数 122030每个立体图形的各条棱都相等、我们把这样的多面体叫做正多面体．各个面也都完全相同。正四面体正六面体正八面体正二十面体4664812812612302222顶点数+面数-棱数=___V + F - E =220根据刚才所数的结果,你能发现什么?2 验证: 将正六面体沿虚线截去一个角, 你会得到一个几面体?七107152欧拉公式顶点数+面数-棱数=__V + F - E =22 在数学的分支------拓扑学中,多面体都可以看作为一类,即多面体都可以拓扑变成一个球.魔术表演
用课本的方法制作两个纸环做一做看哪一组做得快!阅读课本第143页“活动2--- 莫比乌斯带”的第1段和第2段；学一学
思考:
①课本介绍了哪几种做纸环的方法.
②蚂蚁能否不越过纸条边缘从红面爬到蓝面?两端直接粘合纸条扭半圈后两端粘合请您欣赏莫比乌斯带莫比乌斯,德国数学家,（Mobius，1790～1868 )莫比乌斯带是拓扑学中单侧面的一种模型.用剪刀沿图中蚂蚁爬行的路线剪开莫比乌斯带让我们一起变魔术用刚才的方法再剪一次，你又有什么发现？莫比乌斯爬梯小故事莫比乌斯带救人一命的这一节数学活动课,你有什么收获?课后:折一折,数一数,算一算课本第144页 数数看 找规律
图1是有3根火柴棒搭成，图2是由9根火柴棒搭成的.（1）图3是多少根火柴棒搭成的？
（2）如果按照上述规律继续搭下去，
第100个图有多少根火柴棒?
图1 图2 图3答案:15150