3.2.1 对数的概念
图片预览






文档简介
课件18张PPT。苏科版高一数学必修一3.2.1 对数的概念问题1、庄子:一尺之棰,日取其半,万世不竭。
(1)取5次,还有多长?
(2)取多少次,还有0.125尺?抽象出:一、情境创设:x=?问题2、假设2002年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产总值是2002年的2倍?抽象出:x=? 在指数式中,已知底数和指数,通过乘方运
算可求幂;而已知指数和幂,则可通过用开方运
算或分数指数幂运算求底数;
思考:
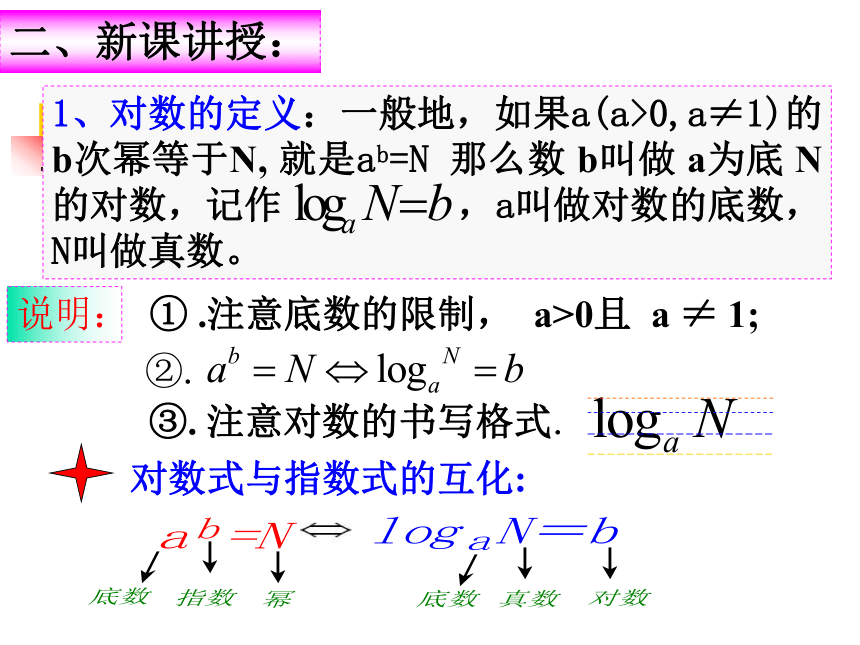
已知底数和幂,如何求指数呢? 1、对数的定义:一般地,如果a(a>0,a≠1)的b次幂等于N, 就是ab=N 那么数 b叫做 a为底 N的对数,记作 ,a叫做对数的底数,N叫做真数。二、新课讲授:① .注意底数的限制, a>0且 a ≠ 1;③. 注意对数的书写格式.说明: 例1:将下列指数式写成对数式:针对性练习:P74 3例2:将下列对数式写成指数式:解:①.常用对数(common logarithm):以10为底的对数log10N, ②. 自然对数(natural logarithm):以无理数e=2.71828… 为底的对数的对数logeN ;
两个重要对数:简记为: lgN . 简记为:
lnN . (在科学技术中,常常使用以e为底的对数)针对性练习:P74 4例3:求下列各式的值:针对性练习:P74 5① .为什么对数的定义中要求底数a>0且 a ≠ 1 ;
②.是否是所有的实数都有对数呢?思考:负数和零没有对数;(1) 26.2=73.5167;(3) 0.53=0.125 ;将下列指数式写成对数式:将下列对数式写成指数式:1、求下列各式的值:三、探索与发现:(1) log31=0(2) lg1=00(3) log0.51=0(4) ln1=你发现了什么?“1”的对数等于零,即loga1=o2、求下列各式的值:(1) log33=1(2) lg10=11(3) log0.50.5=1(4) lne=你发现了什么?底数的对数等于“1”,即logaa=13、求下列各式的值:你发现了什么?30.6894、求下列各式的值:你发现了什么?4585、已知a>0,a≠1,N>0,b∈R.证明:25-3bb总结:对数的基本性质1.负数和零没有对数;2.“1”的对数等于零,即loga1=o3.底数的对数等于“1”,即logaa=1 四、归纳小结
1、 引入对数的必要性;
2 、指数与对数的关系;
3、 对数的基本性质.五、布置作业:
P79 习题3.2(1)1、2、3
(1)取5次,还有多长?
(2)取多少次,还有0.125尺?抽象出:一、情境创设:x=?问题2、假设2002年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产总值是2002年的2倍?抽象出:x=? 在指数式中,已知底数和指数,通过乘方运
算可求幂;而已知指数和幂,则可通过用开方运
算或分数指数幂运算求底数;
思考:
已知底数和幂,如何求指数呢? 1、对数的定义:一般地,如果a(a>0,a≠1)的b次幂等于N, 就是ab=N 那么数 b叫做 a为底 N的对数,记作 ,a叫做对数的底数,N叫做真数。二、新课讲授:① .注意底数的限制, a>0且 a ≠ 1;③. 注意对数的书写格式.说明: 例1:将下列指数式写成对数式:针对性练习:P74 3例2:将下列对数式写成指数式:解:①.常用对数(common logarithm):以10为底的对数log10N, ②. 自然对数(natural logarithm):以无理数e=2.71828… 为底的对数的对数logeN ;
两个重要对数:简记为: lgN . 简记为:
lnN . (在科学技术中,常常使用以e为底的对数)针对性练习:P74 4例3:求下列各式的值:针对性练习:P74 5① .为什么对数的定义中要求底数a>0且 a ≠ 1 ;
②.是否是所有的实数都有对数呢?思考:负数和零没有对数;(1) 26.2=73.5167;(3) 0.53=0.125 ;将下列指数式写成对数式:将下列对数式写成指数式:1、求下列各式的值:三、探索与发现:(1) log31=0(2) lg1=00(3) log0.51=0(4) ln1=你发现了什么?“1”的对数等于零,即loga1=o2、求下列各式的值:(1) log33=1(2) lg10=11(3) log0.50.5=1(4) lne=你发现了什么?底数的对数等于“1”,即logaa=13、求下列各式的值:你发现了什么?30.6894、求下列各式的值:你发现了什么?4585、已知a>0,a≠1,N>0,b∈R.证明:25-3bb总结:对数的基本性质1.负数和零没有对数;2.“1”的对数等于零,即loga1=o3.底数的对数等于“1”,即logaa=1 四、归纳小结
1、 引入对数的必要性;
2 、指数与对数的关系;
3、 对数的基本性质.五、布置作业:
P79 习题3.2(1)1、2、3
