第三章复习《角的概念复习》[上学期]
文档属性
| 名称 | 第三章复习《角的概念复习》[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 176.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-09 23:23:00 | ||
图片预览






文档简介
课件23张PPT。角的概念复习泗阳县新阳中学初一数学组角的概念
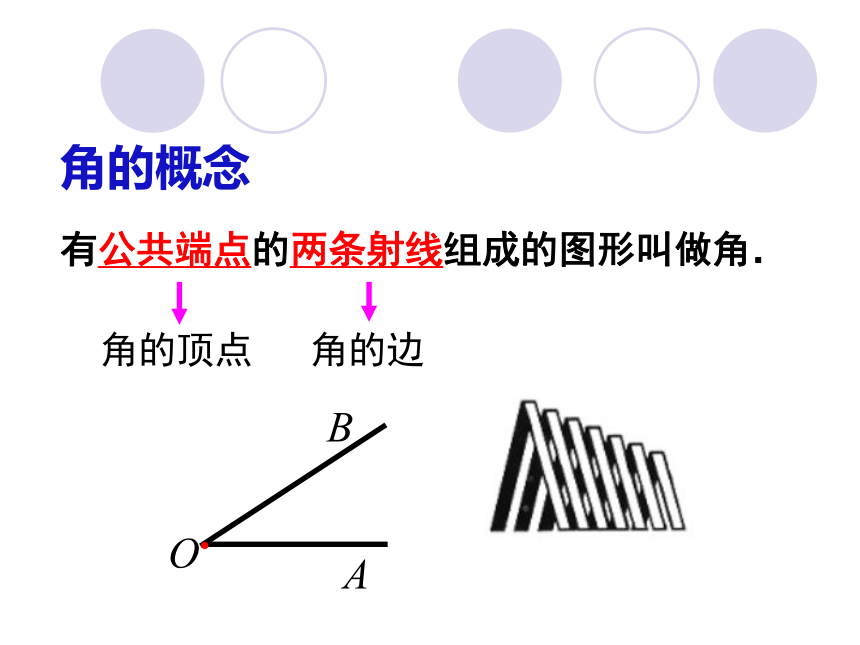
有公共端点的两条射线组成的图形叫做角.角的顶点角的边角的概念 角也可以看成是一条射线绕着端点从起始位置旋转到终止位置所组成的图形;射线的起始位置OA称为角的始边,终止位置OB称为角的终边. 始边终边平角与周角 当角的终边旋转到和始边成一直线时形成的角叫做平角;
当角的终边旋转到和始边再次重合时得到的角叫做周角.角的分类锐角(0°< < 90°)
直角( = 90°)
钝角(90°< < 180°)
平角( = 180°)
周角( = 360°)角的度量单位及其换算1°= 60′, 1′= 60″;
1′= °, 1″= ′.
1周角=2平角=4直角=360°.
1平角=2直角=180°.例1 计算(1)把18.18°化成度、分、秒为________ .
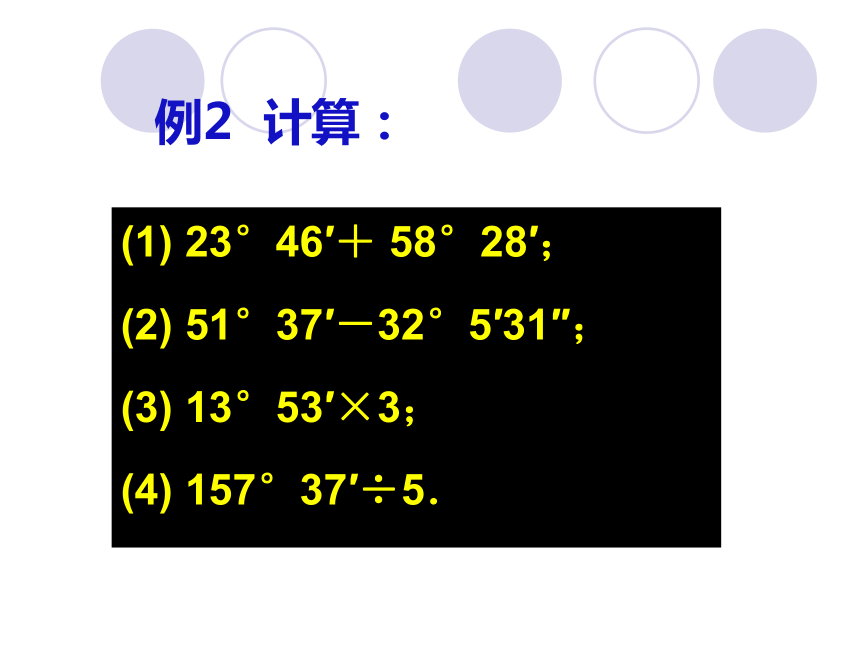
(2)把59°31′30 ″化成度的形式为__________ .18°10′48 ″59.525°例2 计算:(1) 23°46′+ 58°28′;
(2) 51°37′-32°5′31″;
(3) 13°53′×3;
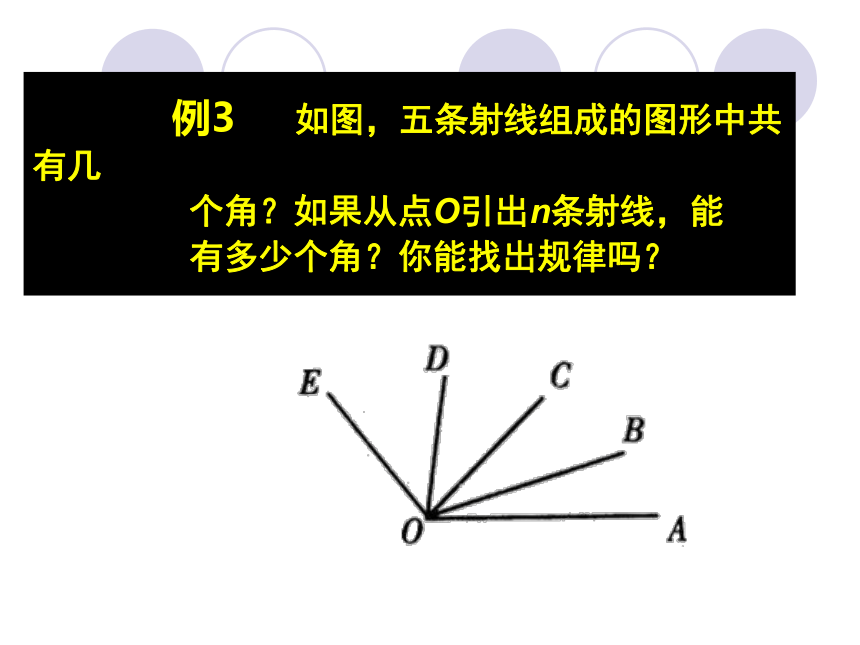
(4) 157°37′÷5. 例3 如图,五条射线组成的图形中共有几 个角?如果从点O引出n条射线,能 有多少个角?你能找出规律吗?角的大小比较 1.度量法——利用“数”比较
2.叠合法——利用“形”比较
3.将两个角叠合起来,使两个角的顶点 及一边重合,另一边落在同旁.两个角的大小关系 ∠ >∠β ,∠ <∠β ,
∠ =∠β 必居其一.注意: 角的大小只与开口大小有关,而与角的边的长短无关.角平分线 从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.∠AOC=∠BOC ∠AOB=2∠AOC=2∠BOC ∠AOB∠AOC=∠BOC= 角的特殊关系 互为余角:如果两个角的和等于90°,就说这两个角互为余角,其中一个是另一个的余角.
互为补角:如果两个角的和等于180°,就说这两个角互为补角,其中一个是另一个的补角.
若∠1+∠2=90°, 则∠1与∠2互为余角.若∠1+∠2=180°,
则∠1与∠2互为补角.角的性质同角(或等角)的余角相等;
同角(或等角)的补角相等.
若∠1+∠2=90°,∠1+∠3=90°,
则∠2 =∠3;
若∠1+∠2=90°,∠3+∠4=90°, ∠1=∠3,则∠2 =∠4.A O B 例4 如图,点O在直线AB上, 且∠AOC=90°,∠EOF =90°, 试找出图中相等的角、互余和互补的角.例5 用一副三角尺可以画出多少度的角? 例6 已知三条射线OA、OB、OC, ∠AOB =2∠AOC,若∠AOB =40°,根据题意画出图形并求∠BOC的度数. 例7 如图,OM是∠AOB的平分线,射线OC在∠BOM内,ON是∠BOC的平分线,已知∠AOC=54°,求∠MON的度数.例8 钟表上的角 在7时到8时之间,时针与分针
(1)何时重合?
(2)何时成直角?课堂小结1.通过本节课的学习,对你的同学说说你有什么收获?
2.通过本节课的学习,对老师说说你还有哪些方面需要老师帮助?作业布置课堂作业:
课本P149第8题、第10题;
课外作业:
《补充习题》P36—40有关习题。
有公共端点的两条射线组成的图形叫做角.角的顶点角的边角的概念 角也可以看成是一条射线绕着端点从起始位置旋转到终止位置所组成的图形;射线的起始位置OA称为角的始边,终止位置OB称为角的终边. 始边终边平角与周角 当角的终边旋转到和始边成一直线时形成的角叫做平角;
当角的终边旋转到和始边再次重合时得到的角叫做周角.角的分类锐角(0°< < 90°)
直角( = 90°)
钝角(90°< < 180°)
平角( = 180°)
周角( = 360°)角的度量单位及其换算1°= 60′, 1′= 60″;
1′= °, 1″= ′.
1周角=2平角=4直角=360°.
1平角=2直角=180°.例1 计算(1)把18.18°化成度、分、秒为________ .
(2)把59°31′30 ″化成度的形式为__________ .18°10′48 ″59.525°例2 计算:(1) 23°46′+ 58°28′;
(2) 51°37′-32°5′31″;
(3) 13°53′×3;
(4) 157°37′÷5. 例3 如图,五条射线组成的图形中共有几 个角?如果从点O引出n条射线,能 有多少个角?你能找出规律吗?角的大小比较 1.度量法——利用“数”比较
2.叠合法——利用“形”比较
3.将两个角叠合起来,使两个角的顶点 及一边重合,另一边落在同旁.两个角的大小关系 ∠ >∠β ,∠ <∠β ,
∠ =∠β 必居其一.注意: 角的大小只与开口大小有关,而与角的边的长短无关.角平分线 从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.∠AOC=∠BOC ∠AOB=2∠AOC=2∠BOC ∠AOB∠AOC=∠BOC= 角的特殊关系 互为余角:如果两个角的和等于90°,就说这两个角互为余角,其中一个是另一个的余角.
互为补角:如果两个角的和等于180°,就说这两个角互为补角,其中一个是另一个的补角.
若∠1+∠2=90°, 则∠1与∠2互为余角.若∠1+∠2=180°,
则∠1与∠2互为补角.角的性质同角(或等角)的余角相等;
同角(或等角)的补角相等.
若∠1+∠2=90°,∠1+∠3=90°,
则∠2 =∠3;
若∠1+∠2=90°,∠3+∠4=90°, ∠1=∠3,则∠2 =∠4.A O B 例4 如图,点O在直线AB上, 且∠AOC=90°,∠EOF =90°, 试找出图中相等的角、互余和互补的角.例5 用一副三角尺可以画出多少度的角? 例6 已知三条射线OA、OB、OC, ∠AOB =2∠AOC,若∠AOB =40°,根据题意画出图形并求∠BOC的度数. 例7 如图,OM是∠AOB的平分线,射线OC在∠BOM内,ON是∠BOC的平分线,已知∠AOC=54°,求∠MON的度数.例8 钟表上的角 在7时到8时之间,时针与分针
(1)何时重合?
(2)何时成直角?课堂小结1.通过本节课的学习,对你的同学说说你有什么收获?
2.通过本节课的学习,对老师说说你还有哪些方面需要老师帮助?作业布置课堂作业:
课本P149第8题、第10题;
课外作业:
《补充习题》P36—40有关习题。
