八年级数学上册试题 第七章 平行线的证明单元测试B卷-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 第七章 平行线的证明单元测试B卷-北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 94.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览




文档简介
第七章 平行线的证明单元测试B卷
一.选择题(共10小题,每小题3分,共30分)
1.下列命题的逆命题是真命题的是( )
A.如果两个角是直角,那么它们相等
B.如果两个实数相等,那么它们的平方相等
C.如果一个四边形是菱形,那么它的四条边都相等
D.如果一个四边形是矩形,那么它的对角线相等
2.下列各命题是假命题的是( )
A.如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
B.每个角都等于60°的三角形是等边三角形
C.如果a3=b3,那么a=b
D.对应角相等的三角形是全等三角形
3.“若|a|>1,则a>1”是一个假命题,可以用举反例的方法说明它是假命题,下列选项中恰当的反例是( )
A.a=5 B.a=﹣5 C.a=1 D.a=﹣1
4.说明命题“若a2>b2,则a>b.”是假命题,举反例正确的是( )
A.a=2,b=3 B.a=﹣2,b=3 C.a=3,b=﹣2 D.a=﹣3,b=2
5.命题“若a=b,则|a|=|b|”与其逆命题的真假性为( )
A.原命题与其逆命题都是真命题
B.原命题与其逆命题都是假命题
C.原命题是假命题,其逆命题是真命题
D.原命题是真命题,其逆命题是假命题
6.下列命题中,真命题的个数是( )
①过一点有且只有一条直线与已知直线平行;②过一边有且只有一条直线与已知直线垂直;③图形平移的方向一定是水平的;④内错角相等;⑤相等的角是对顶角;⑥垂线段最短
A.3 B.2 C.1 D.0
7.已知,在△ABC中,∠B=3∠A,∠C=2∠B,则∠B的度数为( )
A.18° B.36° C.54° D.90°
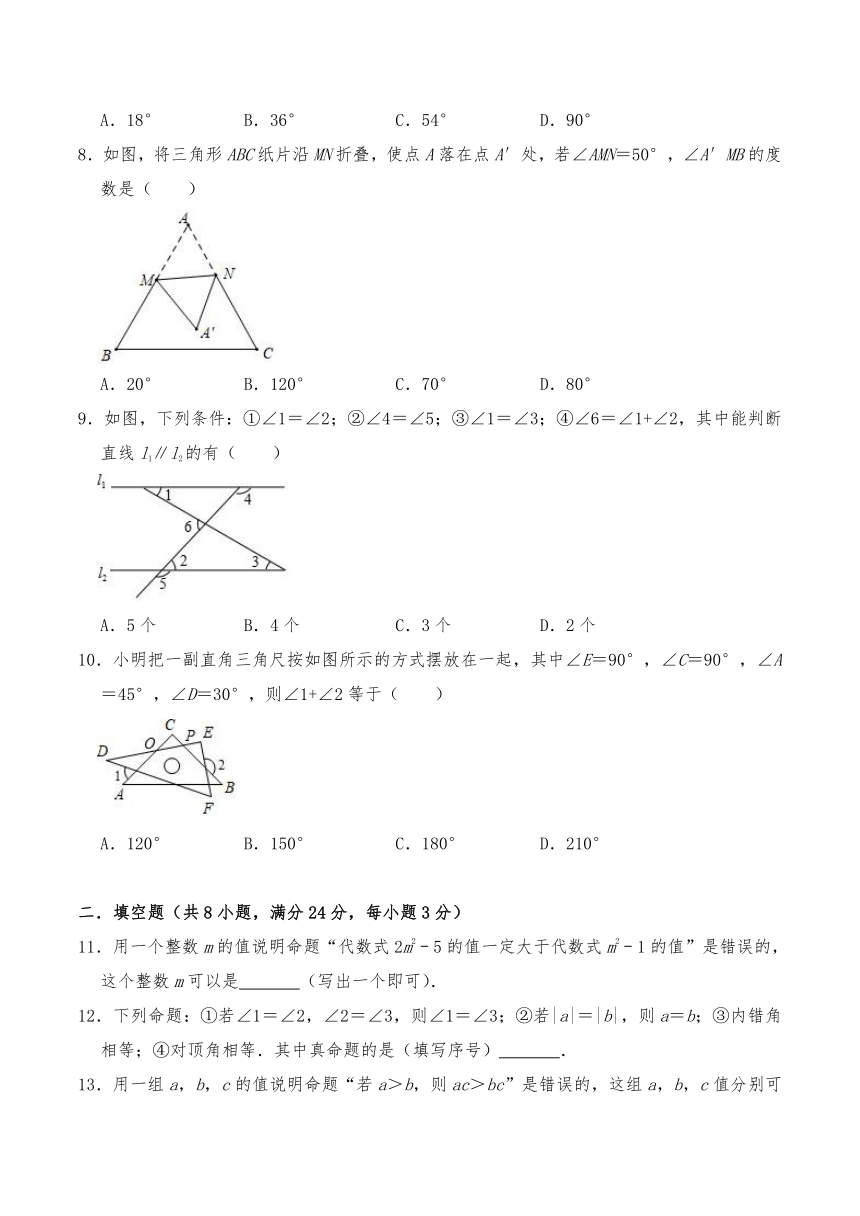
8.如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠AMN=50°,∠A′MB的度数是( )
A.20° B.120° C.70° D.80°
9.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠1=∠3;④∠6=∠1+∠2,其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
10.小明把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于( )
A.120° B.150° C.180° D.210°
二.填空题(共8小题,满分24分,每小题3分)
11.用一个整数m的值说明命题“代数式2m2﹣5的值一定大于代数式m2﹣1的值”是错误的,这个整数m可以是 (写出一个即可).
12.下列命题:①若∠1=∠2,∠2=∠3,则∠1=∠3;②若|a|=|b|,则a=b;③内错角相等;④对顶角相等.其中真命题的是(填写序号) .
13.用一组a,b,c的值说明命题“若a>b,则ac>bc”是错误的,这组a,b,c值分别可以是 .
14.在下列条件中,能确定△ABC是直角三角形的条件有 .(填序号)
①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C
15.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD= 度.
16.如图,一副三角板如图摆放,若∠l=9°44′8″,则∠2= .
17.如图,在△ABC中,∠ACB=90°,∠B=40°,点D在边AB上,将△BCD沿CD折叠,点B落在点B'处.若B′D∥AC,则∠BDC=
18.光线在不间介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射,由于折射率相同,所以水在水中平行的光线,在空气中也是平行的,如图,已知EF∥AB∥CD,∠2=3∠3,∠8=2∠5+10°,则∠7﹣∠4的结果为 度.
三.解答题(共5小题,满分46分)
19.(10分)完成下面的证明.
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°.
证明:过点C作CF∥AB.
∵CF∥AB(已作),
∴∠1= .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE
∴∠D+∠2=180°
∴∠D+∠BCD﹣∠B=180° .
20.(8分)如图,点A在MN上,点B在PQ上,连接AB,过点A作AC⊥AB交PQ于点C,过点B作BD平分∠ABC交AC于点D,且∠NAC+∠ABC=90°.
(1)求证:MN∥PQ;
(2)若∠ABC=∠NAC+10°,求∠ADB的度数.
21.(9分)探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX= °.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
22.(9分)如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)
(1)求证:∠CDA=∠DAB+∠DBA;
(2)如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.
求证:∠AED+∠EAB=180°;
(3)将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
23.(10分)如图,CD∥EF,AE是∠CAB的平分线,∠α和∠β的度数满足方程组
(1)求∠α和∠β的度数;
(2)求证:AB∥CD;
(3)求∠C的度数.
答案
一.选择题
C.D.B.D.D.B.C.D.C.D.
二.填空题
11.m=0(答案不唯一)
12.①④.
13.a=2,b=1,c=﹣2.
14.①②③.
15.66.
16.24°44′8″.
17.115°.
18.28.
三.解答题
19.证明:过点C作CF∥AB,
∵CF∥AB(已作),
∴∠1=∠B,
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B(等量代换),
∵AB∥DE,CF∥AB(已知),
∴CF∥DE(平行于同一条直线的两直线平行),
∴∠D+∠2=180°(两直线平行,同旁内角互补)
∴∠D+∠BCD﹣∠B=180°(等量代换),
20.(1)证明:∵AC⊥AB,
∴∠BAC=90°,
∴∠ABC+∠ACB=90°,
∵∠NAC+∠ABC=90°,
∴∠NAC=∠ACB,
∴MN∥PQ;
(2)解:∵∠ABC=∠NAC+10°=∠ACB+10°,
∵∠ACB+∠ABC=90°,
∴∠ACB+∠ACB+10°=90°,
∴∠ACB=40°,
∴∠ABC=50°,
∵BD平分∠ABC,
∴∠ABD=ABC=25°,
∵∠BAC=90°,
∴∠ADB=90°﹣25°=65°.
21.解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:
过点A、D作射线AF,
∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,
∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,
即∠BDC=∠BAC+∠B+∠C;
(2)①如图(2),∵∠X=90°,
由(1)知:∠A+∠ABX+∠ACX=∠X=90°,
∵∠A=40°,
∴∠ABX+∠ACX=50°,
故答案为:50;
②如图(3),∵∠A=40°,∠DBE=130°,
∴∠ADE+∠AEB=130°﹣40°=90°,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠ADB,∠AEC=∠AEB,
∴∠ADC+∠AEC==45°,
∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.
22.解:(1)∵∠C+∠CAD+∠ADC=∠C+∠CAB+∠B=180°,
∴∠CAD+∠ADC=∠CAB+∠B,
∵∠CDA=∠CAB,
∴∠CAD=∠B,
∵∠CAB=∠CAD+∠DAB=∠ABC+∠DAB,
∴∠CDA=∠DAB+∠DBA;
(2)∵∠CDE=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴∠CDE=∠CAD,又∠B=∠CAD,
∴∴∠B=∠CDE,
∴MN∥BA,
∴∠AED+∠EAB=180°;
(3)∠CAD=∠BDP+∠DPB
证明:由三角形的外角的性质可知,∠ABC=∠BDP+∠DPB,
∵∠CDA=∠CAB,∠C=∠C,
∴△CAD∽△CBA,
∴∠ABC=∠CAD,
∴∠ABC=∠BDP+∠DPB.
23.解:(1)由
①+②得到5α=350°,
∴α=70°,
把α=70°代入①得到β=110°,
∴.
(2)∵α+β=180°,
∴AB∥EF,
∵CD∥EF,
∴AB∥CD.
(3)∵AE是∠CAB的平分线,
∴∠CAB=2α=140°,
∵AB∥CD,
∴∠C+∠CAB=180°,
∴∠C=40°.
一.选择题(共10小题,每小题3分,共30分)
1.下列命题的逆命题是真命题的是( )
A.如果两个角是直角,那么它们相等
B.如果两个实数相等,那么它们的平方相等
C.如果一个四边形是菱形,那么它的四条边都相等
D.如果一个四边形是矩形,那么它的对角线相等
2.下列各命题是假命题的是( )
A.如果一个三角形的两个锐角互余,那么这个三角形是直角三角形
B.每个角都等于60°的三角形是等边三角形
C.如果a3=b3,那么a=b
D.对应角相等的三角形是全等三角形
3.“若|a|>1,则a>1”是一个假命题,可以用举反例的方法说明它是假命题,下列选项中恰当的反例是( )
A.a=5 B.a=﹣5 C.a=1 D.a=﹣1
4.说明命题“若a2>b2,则a>b.”是假命题,举反例正确的是( )
A.a=2,b=3 B.a=﹣2,b=3 C.a=3,b=﹣2 D.a=﹣3,b=2
5.命题“若a=b,则|a|=|b|”与其逆命题的真假性为( )
A.原命题与其逆命题都是真命题
B.原命题与其逆命题都是假命题
C.原命题是假命题,其逆命题是真命题
D.原命题是真命题,其逆命题是假命题
6.下列命题中,真命题的个数是( )
①过一点有且只有一条直线与已知直线平行;②过一边有且只有一条直线与已知直线垂直;③图形平移的方向一定是水平的;④内错角相等;⑤相等的角是对顶角;⑥垂线段最短
A.3 B.2 C.1 D.0
7.已知,在△ABC中,∠B=3∠A,∠C=2∠B,则∠B的度数为( )
A.18° B.36° C.54° D.90°
8.如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠AMN=50°,∠A′MB的度数是( )
A.20° B.120° C.70° D.80°
9.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠1=∠3;④∠6=∠1+∠2,其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
10.小明把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于( )
A.120° B.150° C.180° D.210°
二.填空题(共8小题,满分24分,每小题3分)
11.用一个整数m的值说明命题“代数式2m2﹣5的值一定大于代数式m2﹣1的值”是错误的,这个整数m可以是 (写出一个即可).
12.下列命题:①若∠1=∠2,∠2=∠3,则∠1=∠3;②若|a|=|b|,则a=b;③内错角相等;④对顶角相等.其中真命题的是(填写序号) .
13.用一组a,b,c的值说明命题“若a>b,则ac>bc”是错误的,这组a,b,c值分别可以是 .
14.在下列条件中,能确定△ABC是直角三角形的条件有 .(填序号)
①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C
15.如图,AD是△ABC的高,BE是△ABC的角平分线,BE,AD相交于点F,已知∠BAD=42°,则∠BFD= 度.
16.如图,一副三角板如图摆放,若∠l=9°44′8″,则∠2= .
17.如图,在△ABC中,∠ACB=90°,∠B=40°,点D在边AB上,将△BCD沿CD折叠,点B落在点B'处.若B′D∥AC,则∠BDC=
18.光线在不间介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射,由于折射率相同,所以水在水中平行的光线,在空气中也是平行的,如图,已知EF∥AB∥CD,∠2=3∠3,∠8=2∠5+10°,则∠7﹣∠4的结果为 度.
三.解答题(共5小题,满分46分)
19.(10分)完成下面的证明.
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°.
证明:过点C作CF∥AB.
∵CF∥AB(已作),
∴∠1= .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE
∴∠D+∠2=180°
∴∠D+∠BCD﹣∠B=180° .
20.(8分)如图,点A在MN上,点B在PQ上,连接AB,过点A作AC⊥AB交PQ于点C,过点B作BD平分∠ABC交AC于点D,且∠NAC+∠ABC=90°.
(1)求证:MN∥PQ;
(2)若∠ABC=∠NAC+10°,求∠ADB的度数.
21.(9分)探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图
(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX= °.
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.
22.(9分)如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)
(1)求证:∠CDA=∠DAB+∠DBA;
(2)如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.
求证:∠AED+∠EAB=180°;
(3)将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
23.(10分)如图,CD∥EF,AE是∠CAB的平分线,∠α和∠β的度数满足方程组
(1)求∠α和∠β的度数;
(2)求证:AB∥CD;
(3)求∠C的度数.
答案
一.选择题
C.D.B.D.D.B.C.D.C.D.
二.填空题
11.m=0(答案不唯一)
12.①④.
13.a=2,b=1,c=﹣2.
14.①②③.
15.66.
16.24°44′8″.
17.115°.
18.28.
三.解答题
19.证明:过点C作CF∥AB,
∵CF∥AB(已作),
∴∠1=∠B,
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B(等量代换),
∵AB∥DE,CF∥AB(已知),
∴CF∥DE(平行于同一条直线的两直线平行),
∴∠D+∠2=180°(两直线平行,同旁内角互补)
∴∠D+∠BCD﹣∠B=180°(等量代换),
20.(1)证明:∵AC⊥AB,
∴∠BAC=90°,
∴∠ABC+∠ACB=90°,
∵∠NAC+∠ABC=90°,
∴∠NAC=∠ACB,
∴MN∥PQ;
(2)解:∵∠ABC=∠NAC+10°=∠ACB+10°,
∵∠ACB+∠ABC=90°,
∴∠ACB+∠ACB+10°=90°,
∴∠ACB=40°,
∴∠ABC=50°,
∵BD平分∠ABC,
∴∠ABD=ABC=25°,
∵∠BAC=90°,
∴∠ADB=90°﹣25°=65°.
21.解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:
过点A、D作射线AF,
∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,
∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,
即∠BDC=∠BAC+∠B+∠C;
(2)①如图(2),∵∠X=90°,
由(1)知:∠A+∠ABX+∠ACX=∠X=90°,
∵∠A=40°,
∴∠ABX+∠ACX=50°,
故答案为:50;
②如图(3),∵∠A=40°,∠DBE=130°,
∴∠ADE+∠AEB=130°﹣40°=90°,
∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠ADB,∠AEC=∠AEB,
∴∠ADC+∠AEC==45°,
∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.
22.解:(1)∵∠C+∠CAD+∠ADC=∠C+∠CAB+∠B=180°,
∴∠CAD+∠ADC=∠CAB+∠B,
∵∠CDA=∠CAB,
∴∠CAD=∠B,
∵∠CAB=∠CAD+∠DAB=∠ABC+∠DAB,
∴∠CDA=∠DAB+∠DBA;
(2)∵∠CDE=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴∠CDE=∠CAD,又∠B=∠CAD,
∴∴∠B=∠CDE,
∴MN∥BA,
∴∠AED+∠EAB=180°;
(3)∠CAD=∠BDP+∠DPB
证明:由三角形的外角的性质可知,∠ABC=∠BDP+∠DPB,
∵∠CDA=∠CAB,∠C=∠C,
∴△CAD∽△CBA,
∴∠ABC=∠CAD,
∴∠ABC=∠BDP+∠DPB.
23.解:(1)由
①+②得到5α=350°,
∴α=70°,
把α=70°代入①得到β=110°,
∴.
(2)∵α+β=180°,
∴AB∥EF,
∵CD∥EF,
∴AB∥CD.
(3)∵AE是∠CAB的平分线,
∴∠CAB=2α=140°,
∵AB∥CD,
∴∠C+∠CAB=180°,
∴∠C=40°.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
