北师大版八年级上册数学第四章一次函数测试题(含答案)
文档属性
| 名称 | 北师大版八年级上册数学第四章一次函数测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 15:57:50 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版八年级上册数学第四章测试题(附答案)
一、单选题(共12题;共24分)
1.在平面直角坐标系中,正比例函数y=kx.且y的值随x值的增大而减小的图象是( )
A. B. C. D.
2.一次函数与轴交点的坐标是( )。
A. (0,-3) B. (-3,0) C. (0,3) D. (3,0)
3.一个等腰三角形的周长为10cm ,腰长为xcm ,底边长为ycm,则y与 x的函数关系式和自变量的取值范围为( )。
A. y=5-x(0<x<5) B. y=10-2x(0<x<5)
C. y=5-x(<x<5) D. y=10-2x(<x<5)
4.已知点(-4,y1),(2,y2)都在直线y=-x+b上,则y1,y2大小关系是( )
A. y1>y2 B. y1 =y2 C. y15.如果一个正比例函数的图像经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
6.直线y=kx+b不经过第三象限,则k、b应满足( )
A. k>0,b<0 B. k<0,b>0 C. k<0 b<0 D. k<0,b≥0
7.平行四边形的周长为240,两邻边为x、y,则它们的关系是( ).
A. y=120-x(0C. y =240-x(08.如图,等边△ABC边长为2,四边形DEFG是平行四边形,DG=2,DE=3,∠GDE=60°,BC和DE在同一条直线上,且点C与点D重合,现将△ABC沿D→E的方向以每秒1个单位的速度匀速运动,当点B与点E重合时停止,则在这个运动过程中,△ABC与四边形DEFG的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A. B. C. D.
9.函数y=的自变量x的取值范围是( )
A. x≠0 B. x≠2 C. x>2 D. x<2
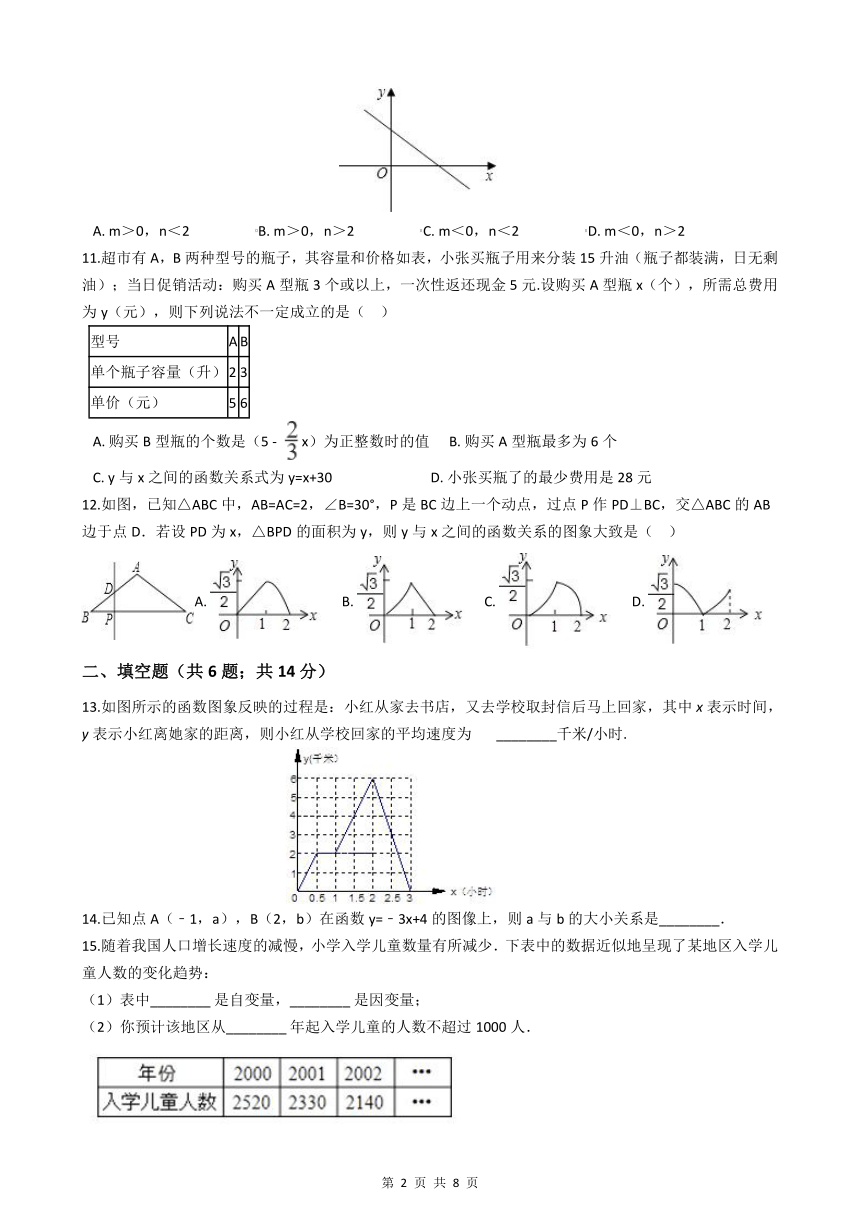
10.已知一次函数y=mx+n﹣2的图象如图所示,则m、n的取值范围是( )
A. m>0,n<2 B. m>0,n>2 C. m<0,n<2 D. m<0,n>2
11.超市有A,B两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,日无剩油);当日促销活动:购买A型瓶3个或以上,一次性返还现金5元.设购买A型瓶x(个),所需总费用为y(元),则下列说法不一定成立的是( )
型号 A B
单个瓶子容量(升) 2 3
单价(元) 5 6
A. 购买B型瓶的个数是(5 - x)为正整数时的值 B. 购买A型瓶最多为6个
C. y与x之间的函数关系式为y=x+30 D. 小张买瓶了的最少费用是28元
12.如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC的AB边于点D.若设PD为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是( )
A. B. C. D.
二、填空题(共6题;共14分)
13.如图所示的函数图象反映的过程是:小红从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小红离她家的距离,则小红从学校回家的平均速度为 ________千米/小时.
14.已知点A(﹣1,a),B(2,b)在函数y=﹣3x+4的图像上,则a与b的大小关系是________.
15.随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:
(1)表中________ 是自变量,________ 是因变量;
(2)你预计该地区从________ 年起入学儿童的人数不超过1000人.
16.若直线y=3x+2不动,将平面直角坐标系xOy沿铅直方向向下平移5个单位,则平移后直线与y轴的交点坐标为________
17.下列函数①y=3x,②2x2+1,③y=x﹣1,④y=2,⑤y=, 是一次函数的是________ .(填序号)
18.已知□ABCD的三个顶点坐标分别为点 A(0,8)、B(0,﹣2)、C(x,y),并且 x,y 满足x﹣y+5=0,则 CD长的最小值为________.
三、解答题(共2题;共10分)
19.已知矩形周长为20,其中一条边长为x,设矩形面积为y
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
20.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)求出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km.
四、作图题(共1题;共14分)
21.小明根据学习函数的经验,对函数y=x+ 的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+ 的自变量x的取值范围是________.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=________,n=________;
x … ﹣3 ﹣2 ﹣1 ﹣ ﹣ 1 2 3 4 …
y … ﹣ ﹣ ﹣2 ﹣ ﹣ m 2 n …
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣ 时,x=________.②写出该函数的一条性质________.
③若方程x+ =t有两个不相等的实数根,则t的取值范围是________.
五、综合题(共4题;共58分)
22.甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
23.[实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.
[数学研究]设t(分钟)后李明、王亮两人与王亮家的距离分别为y1 . y2 , 则y1 . y2与t的函数关系图象如图所示,试根据图象解决下列问题:
(1)填空:王亮的速度v2=________米/分钟;
(2)写出y1与t的函数关系式;
(3)因为李明携带的无线对讲机电量不足,只有在小于1000米范围内才能和王亮的无线对讲机清晰地通话,试探求什么时间段内两人的无线对讲机无法清晰通话.
24.甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,求总运费y关于x的函数关系式;
(2)若要求总运费不超过900元,问共有几种调运方案;
(3)求出总运费最低的调运方案,最低运费是多少元?
25.如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A,B两地相距________千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)当客车行驶多长时间,客、货两车相距150千米.
答 案
一、单选题
1.C 2. B 3. D 4. A 5. D 6. D 7. A 8. B 9. B 10. D 11. C 12. C
二、填空题
13.6 14.a>b 15.年份;入学儿童人数;2008 16. (0,7) 17.①③ 18.
三、解答题
19.解:(1)∵长方形的周长为20cm,若矩形的长为x(其中x>0),则矩形的长为10﹣x,
∴y=x(10﹣x)
(2)∵x与10﹣x表示矩形的长和宽,∴解得:0<x<10.
20. (1)解:由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40,∴a=40×1=40.答:a=40,m=1.
(2)解:当0≤x≤1时设y与x之间的函数关系式为y=k1x,由题意,得
40=k1,∴y=40x当1<x≤1.5时y=40;
当1.5<x≤7设y与x之间的函数关系式为y=k2x+b,由题意,得
,解得: ,∴y=40x﹣20.y= .
(3)解:设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3 , 由题意,得
,解得: ,
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x= .
当40x﹣20+50=80x﹣160时,
解得:x= .
-2= , -2= .
答:乙车行驶 小时或 小时,两车恰好相距50km.
四、作图题
21. (1)x≠0(2);
(3)解:连点成线,画出函数图象.
(4)﹣4或﹣ ;函数图象在第一、三象限且关于原点对称;t<﹣2或t>2.
五、综合题
22. (1)解:甲行走的速度:150÷5=30(米/分)
(2)解:当t=35时,甲行走的路程为:30×35=1050(米),乙行走的路程为:(35﹣5)×50=1500(米),
∴当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500﹣1050)=450米,
∴甲到达图书馆还需时间;450÷30=15(分),∴35+15=50(分),∴当s=0时,横轴上对应的时间为50.
补画的图象如图所示(横轴上对应的时间为50),
(3)解:如图2,
设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,
解得:x=7.5,
7.5+5=12.5(分),
由函数图象可知,当t=12.5时,s=0,
∴点B的坐标为(12.5,0),
当12.5≤t≤35时,设BC的解析式为:s=kt+b,(k≠0),
把C(35,450),B(12.5,0)代入可得:
解得: ,
∴s=20t﹣250,
当35<t≤50时,设CD的解析式为s=k1x+b1 , (k1≠0),
把D(50,0),C(35,450)代入得: 解得:
∴s=﹣30t+1500,
∵甲、乙两人相距360米,即s=360,
解得:t1=30.5,t2=38,
∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米
23. (1)200
(2)解:v1=1.5,v2=1.5×200=300(米/分钟),3000÷300=10(分钟),a=10,
当0≤t<10时,设y1=k1t+b1 , 则将点(0,3000),(10,0)的坐标代入得
解得k1=﹣300,b1=3000,所以y1=﹣300t+3000,0≤t<10,
当10≤t≤30时,设y1=k2t+b2 , 则将点(10,0),(30,6000)的坐标代入得 ,
解得k2=300,b2=﹣3000,所以y1=300t﹣3000,10≤t≤30;
综上:
(3)解:由于y2的图象为过原点的直线,可设y2=kt
又因为其图象过点(30,6000),将其坐标代入关系式:6000=30k
解得k=200,所以y2=200t,
当0≤t<10时,y2+y1=200t+(﹣300t+3000)=﹣100t+3000>2000,
此时两人的无线对讲机无法清晰通话;
当10≤t≤30时,y2﹣y1=200t﹣(300﹣3000)=﹣100t+3000>1000,
解得10≤t<20;
综上所述:当0≤t<20时,两人的无线对讲机无法清晰通话
24. (1)解:若乙仓库调往A县农用车x辆(x≤6),则乙仓库调往B县农用车6﹣x辆,A县需10辆车,故甲给A县调农用车10﹣x辆,
那么甲县给B县调车x+2辆,根据各个调用方式的运费可以列出方程如下:y=40(10﹣x)+80(x+2)+30x+50(6﹣x),
化简得:y=20x+860(0≤x≤6)
(2)解:总运费不超过900,即y≤900,代入函数关系式得20x+860≤900,
解得x≤2,所以x=0,1,2,
即如下三种方案:
1)、甲往A:10辆;乙往A:0辆甲往B:2辆;乙往B:6辆,
2)、甲往A:9;乙往A:1甲往B:3;乙往B:5,
3)、甲往A:8;乙往A:2甲往B:4;乙往B:4
(3)解:要使得总运费最低,由y=20x+860(0≤x≤6)知,x=0时y值最小为860,
即上面(2)的第一种方案:甲往A:10辆;乙往A:0辆;甲往B:2辆;乙往B:6辆,
总运费最少为860元
25. (1)420
(2)解:设两小时后,货车离C站的路程y 与行驶时间x之间的函数关系式是y =kx+b,
由图象可知,货车的速度为:60÷2=30千米/时,
∴货车到达A的时间为:420÷30=14(小时),
∴点P的坐标为(14,360),
∴ ,得 ,
即两小时后,货车离C站的路程y 与行驶时间x之间的函数关系式是y =30x 60
(3)解:由题意可得,
(420 150)×(60÷2+360÷6)=3(小时),
当客车行驶3小时时,客、货两车相距150千米。
(
第
- 1 -
页 共
10
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大版八年级上册数学第四章测试题(附答案)
一、单选题(共12题;共24分)
1.在平面直角坐标系中,正比例函数y=kx.且y的值随x值的增大而减小的图象是( )
A. B. C. D.
2.一次函数与轴交点的坐标是( )。
A. (0,-3) B. (-3,0) C. (0,3) D. (3,0)
3.一个等腰三角形的周长为10cm ,腰长为xcm ,底边长为ycm,则y与 x的函数关系式和自变量的取值范围为( )。
A. y=5-x(0<x<5) B. y=10-2x(0<x<5)
C. y=5-x(<x<5) D. y=10-2x(<x<5)
4.已知点(-4,y1),(2,y2)都在直线y=-x+b上,则y1,y2大小关系是( )
A. y1>y2 B. y1 =y2 C. y1
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
6.直线y=kx+b不经过第三象限,则k、b应满足( )
A. k>0,b<0 B. k<0,b>0 C. k<0 b<0 D. k<0,b≥0
7.平行四边形的周长为240,两邻边为x、y,则它们的关系是( ).
A. y=120-x(0
A. B. C. D.
9.函数y=的自变量x的取值范围是( )
A. x≠0 B. x≠2 C. x>2 D. x<2
10.已知一次函数y=mx+n﹣2的图象如图所示,则m、n的取值范围是( )
A. m>0,n<2 B. m>0,n>2 C. m<0,n<2 D. m<0,n>2
11.超市有A,B两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,日无剩油);当日促销活动:购买A型瓶3个或以上,一次性返还现金5元.设购买A型瓶x(个),所需总费用为y(元),则下列说法不一定成立的是( )
型号 A B
单个瓶子容量(升) 2 3
单价(元) 5 6
A. 购买B型瓶的个数是(5 - x)为正整数时的值 B. 购买A型瓶最多为6个
C. y与x之间的函数关系式为y=x+30 D. 小张买瓶了的最少费用是28元
12.如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC的AB边于点D.若设PD为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是( )
A. B. C. D.
二、填空题(共6题;共14分)
13.如图所示的函数图象反映的过程是:小红从家去书店,又去学校取封信后马上回家,其中x表示时间,y表示小红离她家的距离,则小红从学校回家的平均速度为 ________千米/小时.
14.已知点A(﹣1,a),B(2,b)在函数y=﹣3x+4的图像上,则a与b的大小关系是________.
15.随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:
(1)表中________ 是自变量,________ 是因变量;
(2)你预计该地区从________ 年起入学儿童的人数不超过1000人.
16.若直线y=3x+2不动,将平面直角坐标系xOy沿铅直方向向下平移5个单位,则平移后直线与y轴的交点坐标为________
17.下列函数①y=3x,②2x2+1,③y=x﹣1,④y=2,⑤y=, 是一次函数的是________ .(填序号)
18.已知□ABCD的三个顶点坐标分别为点 A(0,8)、B(0,﹣2)、C(x,y),并且 x,y 满足x﹣y+5=0,则 CD长的最小值为________.
三、解答题(共2题;共10分)
19.已知矩形周长为20,其中一条边长为x,设矩形面积为y
(1)写出y与x的函数关系式;
(2)求自变量x的取值范围.
20.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
(1)求出图中m,a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数解析式,并写出相应的x的取值范围;
(3)当乙车行驶多长时间时,两车恰好相距50km.
四、作图题(共1题;共14分)
21.小明根据学习函数的经验,对函数y=x+ 的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+ 的自变量x的取值范围是________.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=________,n=________;
x … ﹣3 ﹣2 ﹣1 ﹣ ﹣ 1 2 3 4 …
y … ﹣ ﹣ ﹣2 ﹣ ﹣ m 2 n …
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣ 时,x=________.②写出该函数的一条性质________.
③若方程x+ =t有两个不相等的实数根,则t的取值范围是________.
五、综合题(共4题;共58分)
22.甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画s关于t的函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
23.[实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.
[数学研究]设t(分钟)后李明、王亮两人与王亮家的距离分别为y1 . y2 , 则y1 . y2与t的函数关系图象如图所示,试根据图象解决下列问题:
(1)填空:王亮的速度v2=________米/分钟;
(2)写出y1与t的函数关系式;
(3)因为李明携带的无线对讲机电量不足,只有在小于1000米范围内才能和王亮的无线对讲机清晰地通话,试探求什么时间段内两人的无线对讲机无法清晰通话.
24.甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,求总运费y关于x的函数关系式;
(2)若要求总运费不超过900元,问共有几种调运方案;
(3)求出总运费最低的调运方案,最低运费是多少元?
25.如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A,B两地相距________千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)当客车行驶多长时间,客、货两车相距150千米.
答 案
一、单选题
1.C 2. B 3. D 4. A 5. D 6. D 7. A 8. B 9. B 10. D 11. C 12. C
二、填空题
13.6 14.a>b 15.年份;入学儿童人数;2008 16. (0,7) 17.①③ 18.
三、解答题
19.解:(1)∵长方形的周长为20cm,若矩形的长为x(其中x>0),则矩形的长为10﹣x,
∴y=x(10﹣x)
(2)∵x与10﹣x表示矩形的长和宽,∴解得:0<x<10.
20. (1)解:由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40,∴a=40×1=40.答:a=40,m=1.
(2)解:当0≤x≤1时设y与x之间的函数关系式为y=k1x,由题意,得
40=k1,∴y=40x当1<x≤1.5时y=40;
当1.5<x≤7设y与x之间的函数关系式为y=k2x+b,由题意,得
,解得: ,∴y=40x﹣20.y= .
(3)解:设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3 , 由题意,得
,解得: ,
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x= .
当40x﹣20+50=80x﹣160时,
解得:x= .
-2= , -2= .
答:乙车行驶 小时或 小时,两车恰好相距50km.
四、作图题
21. (1)x≠0(2);
(3)解:连点成线,画出函数图象.
(4)﹣4或﹣ ;函数图象在第一、三象限且关于原点对称;t<﹣2或t>2.
五、综合题
22. (1)解:甲行走的速度:150÷5=30(米/分)
(2)解:当t=35时,甲行走的路程为:30×35=1050(米),乙行走的路程为:(35﹣5)×50=1500(米),
∴当t=35时,乙已经到达图书馆,甲距图书馆的路程还有(1500﹣1050)=450米,
∴甲到达图书馆还需时间;450÷30=15(分),∴35+15=50(分),∴当s=0时,横轴上对应的时间为50.
补画的图象如图所示(横轴上对应的时间为50),
(3)解:如图2,
设乙出发经过x分和甲第一次相遇,根据题意得:150+30x=50x,
解得:x=7.5,
7.5+5=12.5(分),
由函数图象可知,当t=12.5时,s=0,
∴点B的坐标为(12.5,0),
当12.5≤t≤35时,设BC的解析式为:s=kt+b,(k≠0),
把C(35,450),B(12.5,0)代入可得:
解得: ,
∴s=20t﹣250,
当35<t≤50时,设CD的解析式为s=k1x+b1 , (k1≠0),
把D(50,0),C(35,450)代入得: 解得:
∴s=﹣30t+1500,
∵甲、乙两人相距360米,即s=360,
解得:t1=30.5,t2=38,
∴当甲行走30.5分钟或38分钟时,甲、乙两人相距360米
23. (1)200
(2)解:v1=1.5,v2=1.5×200=300(米/分钟),3000÷300=10(分钟),a=10,
当0≤t<10时,设y1=k1t+b1 , 则将点(0,3000),(10,0)的坐标代入得
解得k1=﹣300,b1=3000,所以y1=﹣300t+3000,0≤t<10,
当10≤t≤30时,设y1=k2t+b2 , 则将点(10,0),(30,6000)的坐标代入得 ,
解得k2=300,b2=﹣3000,所以y1=300t﹣3000,10≤t≤30;
综上:
(3)解:由于y2的图象为过原点的直线,可设y2=kt
又因为其图象过点(30,6000),将其坐标代入关系式:6000=30k
解得k=200,所以y2=200t,
当0≤t<10时,y2+y1=200t+(﹣300t+3000)=﹣100t+3000>2000,
此时两人的无线对讲机无法清晰通话;
当10≤t≤30时,y2﹣y1=200t﹣(300﹣3000)=﹣100t+3000>1000,
解得10≤t<20;
综上所述:当0≤t<20时,两人的无线对讲机无法清晰通话
24. (1)解:若乙仓库调往A县农用车x辆(x≤6),则乙仓库调往B县农用车6﹣x辆,A县需10辆车,故甲给A县调农用车10﹣x辆,
那么甲县给B县调车x+2辆,根据各个调用方式的运费可以列出方程如下:y=40(10﹣x)+80(x+2)+30x+50(6﹣x),
化简得:y=20x+860(0≤x≤6)
(2)解:总运费不超过900,即y≤900,代入函数关系式得20x+860≤900,
解得x≤2,所以x=0,1,2,
即如下三种方案:
1)、甲往A:10辆;乙往A:0辆甲往B:2辆;乙往B:6辆,
2)、甲往A:9;乙往A:1甲往B:3;乙往B:5,
3)、甲往A:8;乙往A:2甲往B:4;乙往B:4
(3)解:要使得总运费最低,由y=20x+860(0≤x≤6)知,x=0时y值最小为860,
即上面(2)的第一种方案:甲往A:10辆;乙往A:0辆;甲往B:2辆;乙往B:6辆,
总运费最少为860元
25. (1)420
(2)解:设两小时后,货车离C站的路程y 与行驶时间x之间的函数关系式是y =kx+b,
由图象可知,货车的速度为:60÷2=30千米/时,
∴货车到达A的时间为:420÷30=14(小时),
∴点P的坐标为(14,360),
∴ ,得 ,
即两小时后,货车离C站的路程y 与行驶时间x之间的函数关系式是y =30x 60
(3)解:由题意可得,
(420 150)×(60÷2+360÷6)=3(小时),
当客车行驶3小时时,客、货两车相距150千米。
(
第
- 1 -
页 共
10
页
)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
