八年级数学上册试题 第四章 一次函数单元测试B卷-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 第四章 一次函数单元测试B卷-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 15:32:22 | ||
图片预览




文档简介
第四章 一次函数单元测试B卷
一.选择题(共10小题,每小题3分,共30分)
1.若点(m,n)在坐标系中的第四象限,则一次函数y=(m+2)x+n﹣4的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知一次函数y=kx+2的图象经过点A,且y随x的增大而减小.则A点的坐标可以是( )
A.(2,5) B.(﹣1,1) C.(3,0) D.(,4)
3.一次函数y=mx+n与正比例函数y=mnx(m、n为常数,且m≠0),它们在同一坐标系中的大致图象是( )
A. B.
C. D.
4.一次函数y=kx+b的图象经过第一、二、四象限,若点A (2,m),B(﹣1,n)在该一次函数的图象上,则m、n的大小关系是( )
A.m<n B.m=n C.m>n. D.无法判定
5.已知一次函数y=kx+b(k,b为常数)的图象经过平面直角坐标系的第一、二、三象限,则下列结论一定正确的是( )
A.kb>0 B.kb<0 C.k﹣b>0 D.k+b<0
6.已知一次函数y=(3m﹣7)x﹣1+m(m为整数)的图象与y轴正半轴相交,y随x的的增大而减小,当0<y<4时,x的取值范围( )
A.﹣1<x<0 B.﹣3<x<1 C.0<x<4 D.1<x<3
7.在某次试验中,测得两个变量x和y之间的4组对应数据如下表:
x 1 2 3 4
y 0 3 8 15
则y与x之间的关系满足下列关系式( )
A.y=2x﹣2 B.y=3x﹣3 C.y=x2﹣1 D.y=x+1
8.若k>1,则一次函数y=(k﹣1)x+1﹣k的图象是( )
A. B.
C. D.
9.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示,下列结论正确的是( )
A.降价后西瓜的单价为2元/千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
10.甲、乙两车同时从A地出发,各自都以自己的速度匀速向B地行驶,甲车先到B地,停车1小时后按原速匀速返回,直到两车相遇.已知,乙车的速度是60千米/时,如图是两车之间的距离y(千米)与乙车行驶的时间x(小时)之间的函数图象,则下列说法不正确的是( )
A.A、B两地之间的距离是450千米
B.乙车从出发到与甲车返回时相遇所用的时间是6.6小时
C.甲车的速度是80千米/时
D.点M的坐标是(6,90)
二.填空题(共8小题,满分24分,每小题3分)
11.当k= 时,函数y=(k+1)x2﹣|k|+4是一次函数.
12.若y=(m﹣3)x|m|﹣2+m+n是正比例函数,则m= ,n= .
13.在平面直角坐标系中,A,B,C三点分别为(﹣4,0),(﹣4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP,垂足为P,则点P的坐标为 .
14.一次函数y=kx+b的图象交x轴于点A(﹣2,0),交y轴于点B,与两坐标轴所围成的三角形的面积为8,则该函数的表达式为 .
15.如图,在平面直角坐标中,点O为坐标原点,直线y=kx﹣4k(k<0)交x轴的正半轴于点A,交y轴的正半轴于点B,若AC平分∠BAO交OB于点C,BC=2OC,则k的值为 .
16.一条笔直的公路上顺次有A、B、C三地,甲、乙两车同时从B地出发,向A地均速行驶.甲车到达A地后停止,乙车到达A地后停留1小时,然后再调头按原速向C地行驶.若A、B两地相距400千米,在两车行驶过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则他们出发后经过 小时相遇.
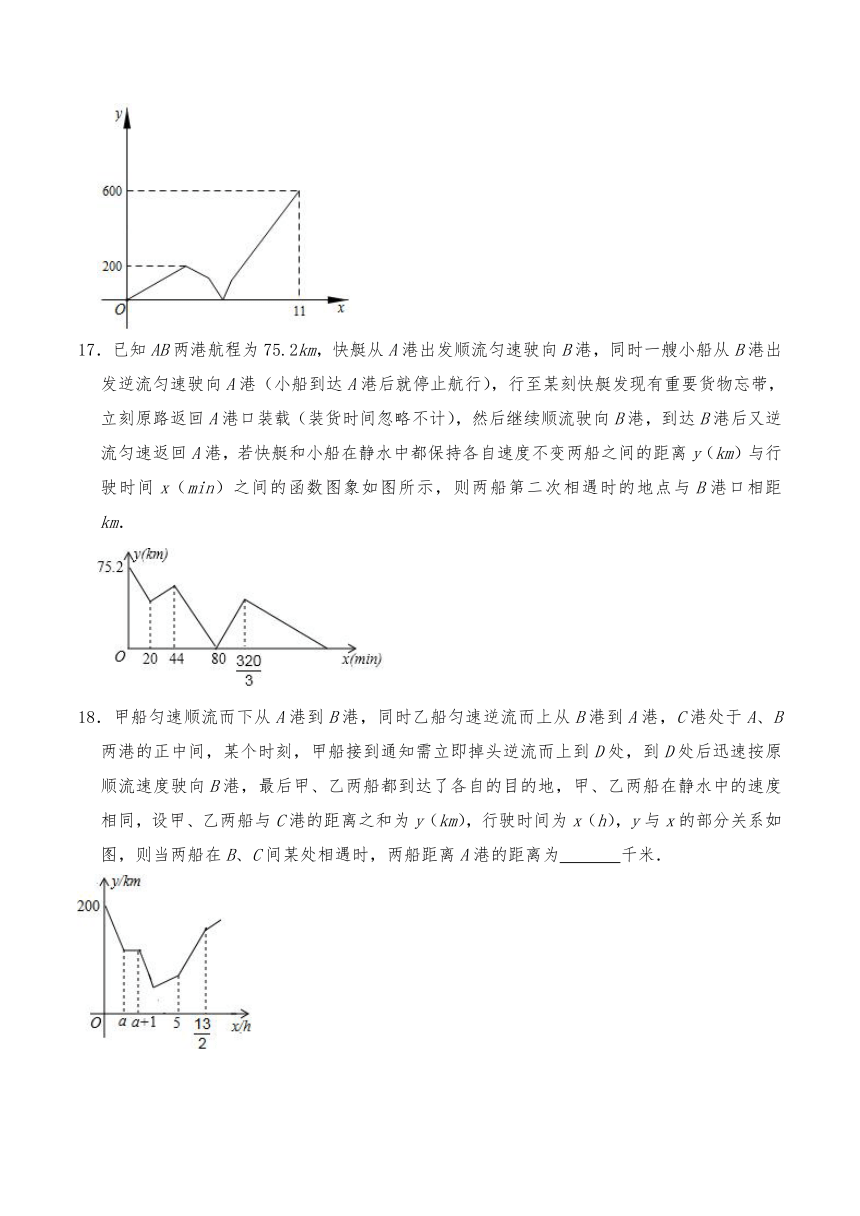
17.已知AB两港航程为75.2km,快艇从A港出发顺流匀速驶向B港,同时一艘小船从B港出发逆流匀速驶向A港(小船到达A港后就停止航行),行至某刻快艇发现有重要货物忘带,立刻原路返回A港口装载(装货时间忽略不计),然后继续顺流驶向B港,到达B港后又逆流匀速返回A港,若快艇和小船在静水中都保持各自速度不变两船之间的距离y(km)与行驶时间x(min)之间的函数图象如图所示,则两船第二次相遇时的地点与B港口相距 km.
18.甲船匀速顺流而下从A港到B港,同时乙船匀速逆流而上从B港到A港,C港处于A、B两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到D处,到D处后迅速按原顺流速度驶向B港,最后甲、乙两船都到达了各自的目的地,甲、乙两船在静水中的速度相同,设甲、乙两船与C港的距离之和为y(km),行驶时间为x(h),y与x的部分关系如图,则当两船在B、C间某处相遇时,两船距离A港的距离为 千米.
三.解答题(共5小题,满分46分)
19.(8分)已知正比例函数y=kx的图象经过第四象限内一点P(k+2,7k+6),求k的值.
20.(8分)如图,直线y=x+b与x轴交于点A,与y轴于点B,点C(﹣2,0)在线段OA上,且OC=OA.
(1)求b的值;
(2)点P是直线y=x+b上一动点,连接PC,PO,求PC+PO的最小值.
21.(9分)甲乙两车间同时开始加工﹣批服装,从开始加工到完成这批服装甲车间工作了8小时,乙车间在中途停工一段时间维修设备,然后在甲车间加工到4小时时按停工前的工作效率继续加工,直至与甲车间同时完成这批服装的加工任务.设甲、乙两车间各自加工服装的数量为y(件),甲车间加工的时间为x(时),y与x的函数图象如图所示.
(1)甲车间每小时加工服装的件数为 件,这批服装的总件数为 件:
(2)乙车间花了多少时间维修设备?
(3)求甲、乙两车间在正常情况下,共同完成加工800件服装时甲车间所用的时间.
22.(9分)2018年8月31日,十三届全国人大常委会第五次会议表决通过全国人大常委会关于修改个人所得税法的决定根据决定,个税“起征点”由3500元/月提高至5000元/月.2019年1月1日起,新版个人所得税税率表正式实施下面是2019最新个人所得税税率表:
级数 月应纳税所得额 税率
1 不超过3000元的部分 3%
2 超过3000至12000元的部分 10%
3 超过12000至25000元的部分 20%
4 超过25000至35000元的部分 25%
5 超过35000至55000元的部分 30%
6 超过55000至80000元的部分 35%
7 超过80000元的部分 45%
月应纳税所得额是指居民个人月工资减去5000元后的余额.
如笑笑的妈妈10月份工资是9000元,则应纳税所得额为9000﹣5000=4000(元),所以笑笑的妈妈应缴纳个人所得税为3000×3%+1000×10%=190(元)
(1)笑笑的表哥10月份工资收人6800元,则他需缴纳的个人所得税是 元;
(2)设笑笑的爸爸10月份工资收人为x元(10000<x≤15000),他10月份需要缴纳的个人所得税为y元,求y与x的函数关系式;
(3)某软件工程师10月份缴纳个人所得税12790元,则他的税前收入是 元.
23.(12分)一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象
(1)李越骑车的速度为 米/分钟;F点的坐标为 ;
(2)求李越从乙地骑往甲地时,s与t之间的函数表达式;
(3)求王明从甲地到乙地时,s与t之间的函数表达式;
(4)求李越与王明第二次相遇时t的值.
答案
一.选择题
B.C.A.A.A.B.C.A.C.C.
二.填空题
11.1.
12.﹣3,3.
13.(2,0)或(2﹣2,0)或(2+2,0).
14.y=4x+8或y=﹣4x﹣8.
15.﹣.
16.
17..
18..
三.解答题
19.解:∵正比例函数y=kx的图象经过点P(k+2,7k+6),
∴7k+6=k(k+2),
整理,得:k2﹣5k﹣6=0,
解得:k1=﹣1,k2=6.
∵点P(k+2,7k+6)在第四象限,
∴,
解得:﹣2<k<﹣,
∴k=﹣1.
∴k的值为﹣1.
20.解:(1)∵点C(﹣2,0)在线段OA上,且OC=OA,
∴OA=3OC=3×2=6,
∴A(﹣6,0),
∵直线y=x+b与x轴交于点A,
∴﹣6+b=0,
∴b=6;
(2)过O作直线AB的对称点O′,连接O′C交AB于点P,此时PC+PO的值最小,最小值为O′C的长,
∵直线为y=x+6,
∴B(0,6),
∴OA=OB=6,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵OO′和AB互相垂直平分,
∴四边形AOBO′是正方形,
∴O′(﹣6,6),
∴O′C==2,
故PC+PO的最小值为2.
21.解:(1)甲车间每小时加工服装件数为720÷8=90(件),
这批服装的总件数为720+390=1110(件).
故答案为:90;1110.
(2)乙车间每小时加工服装件数为:(件),
乙车间维修设备前的工作时间:(时).
乙车间维修设备时间为:4﹣2=2(小时).
答:乙车间花了2时间维修设备;
(3)设乙车间维修设备后y与x的函数关系式为y=kx+b,根据题意得:
,解得,
∴乙车间维修设备后y与x的函数关系式为y=65x﹣130;
由题意可得甲车间加工服装数量y与x之间的函数关系式为y=90x,
设甲,乙两车间共同完成加工服装w件,则:
w=90x+(65x﹣130)=155x﹣130,
当w=800时,155x﹣130=800,
解得x=6,
答:甲、乙两车间在正常情况下,共同完成加工800件服装时甲车间所用的时间为6小时.
22.解:(1)由题意可得,
笑笑的表哥10月份工资收人6800元,则他需缴纳的个人所得税是:(6800﹣5000)×3%=1800×3%=54(元),
故答案为:54;
(2)∵10000<x≤15000,
∴5000<x﹣5000≤10000,
∴y与x的函数关系式为:3000×3%+(x﹣5000﹣3000)×10%=0.1x﹣710,
即y与x的函数关系式为:y=0.1x﹣710;
(3)∵3000×3%=90,
3000×3%+(12000﹣3000)×10%=990,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%=3590,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%+(35000﹣25000)×25%=6090,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%+(35000﹣25000)×25%+(55000﹣35000)×30%=12090,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%+(35000﹣25000)×25%+(55000﹣35000)×30%+(80000﹣55000)×35%=20840,
∵12090<12790<20840,
∴该软件工程师的税前收入在60000~85000之间,
设该软件工程师的税前收入是x元,
12090+(x﹣5000﹣35000)×35%=12790,
解得,x=42000,
故答案为:42000.
23.解:(1)由图象可得,
李越骑车的速度为:2400÷10=240米/分钟,2400÷96=25,所以F点的坐标为(25,0).
故答案为:240;(25,0);
(2)设李越从乙地骑往甲地时,s与t之间的函数表达式为s=kt,
2400=10k,得k=240,
即李越从乙地骑往甲地时,s与t之间的函数表达式为s=240t,
故答案为:s=240t;
(3)设王明从甲地到乙地时,s与t之间的函数表达式为s=kt+2400,根据题意得,
25k+2400=0,
解得k=﹣96,
所以王明从甲地到乙地时,s与t之间的函数表达式为:s=﹣96x+2400;
(4)根据题意得,240(t﹣2)﹣96t=2400,
解得t=20.
答:李越与王明第二次相遇时t的值为20.
一.选择题(共10小题,每小题3分,共30分)
1.若点(m,n)在坐标系中的第四象限,则一次函数y=(m+2)x+n﹣4的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知一次函数y=kx+2的图象经过点A,且y随x的增大而减小.则A点的坐标可以是( )
A.(2,5) B.(﹣1,1) C.(3,0) D.(,4)
3.一次函数y=mx+n与正比例函数y=mnx(m、n为常数,且m≠0),它们在同一坐标系中的大致图象是( )
A. B.
C. D.
4.一次函数y=kx+b的图象经过第一、二、四象限,若点A (2,m),B(﹣1,n)在该一次函数的图象上,则m、n的大小关系是( )
A.m<n B.m=n C.m>n. D.无法判定
5.已知一次函数y=kx+b(k,b为常数)的图象经过平面直角坐标系的第一、二、三象限,则下列结论一定正确的是( )
A.kb>0 B.kb<0 C.k﹣b>0 D.k+b<0
6.已知一次函数y=(3m﹣7)x﹣1+m(m为整数)的图象与y轴正半轴相交,y随x的的增大而减小,当0<y<4时,x的取值范围( )
A.﹣1<x<0 B.﹣3<x<1 C.0<x<4 D.1<x<3
7.在某次试验中,测得两个变量x和y之间的4组对应数据如下表:
x 1 2 3 4
y 0 3 8 15
则y与x之间的关系满足下列关系式( )
A.y=2x﹣2 B.y=3x﹣3 C.y=x2﹣1 D.y=x+1
8.若k>1,则一次函数y=(k﹣1)x+1﹣k的图象是( )
A. B.
C. D.
9.广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完,销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示,下列结论正确的是( )
A.降价后西瓜的单价为2元/千克
B.广宇一共进了50千克西瓜
C.售完西瓜后广字获得的总利润为44元
D.降价前的单价比降价后的单价多0.6元
10.甲、乙两车同时从A地出发,各自都以自己的速度匀速向B地行驶,甲车先到B地,停车1小时后按原速匀速返回,直到两车相遇.已知,乙车的速度是60千米/时,如图是两车之间的距离y(千米)与乙车行驶的时间x(小时)之间的函数图象,则下列说法不正确的是( )
A.A、B两地之间的距离是450千米
B.乙车从出发到与甲车返回时相遇所用的时间是6.6小时
C.甲车的速度是80千米/时
D.点M的坐标是(6,90)
二.填空题(共8小题,满分24分,每小题3分)
11.当k= 时,函数y=(k+1)x2﹣|k|+4是一次函数.
12.若y=(m﹣3)x|m|﹣2+m+n是正比例函数,则m= ,n= .
13.在平面直角坐标系中,A,B,C三点分别为(﹣4,0),(﹣4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP,垂足为P,则点P的坐标为 .
14.一次函数y=kx+b的图象交x轴于点A(﹣2,0),交y轴于点B,与两坐标轴所围成的三角形的面积为8,则该函数的表达式为 .
15.如图,在平面直角坐标中,点O为坐标原点,直线y=kx﹣4k(k<0)交x轴的正半轴于点A,交y轴的正半轴于点B,若AC平分∠BAO交OB于点C,BC=2OC,则k的值为 .
16.一条笔直的公路上顺次有A、B、C三地,甲、乙两车同时从B地出发,向A地均速行驶.甲车到达A地后停止,乙车到达A地后停留1小时,然后再调头按原速向C地行驶.若A、B两地相距400千米,在两车行驶过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则他们出发后经过 小时相遇.
17.已知AB两港航程为75.2km,快艇从A港出发顺流匀速驶向B港,同时一艘小船从B港出发逆流匀速驶向A港(小船到达A港后就停止航行),行至某刻快艇发现有重要货物忘带,立刻原路返回A港口装载(装货时间忽略不计),然后继续顺流驶向B港,到达B港后又逆流匀速返回A港,若快艇和小船在静水中都保持各自速度不变两船之间的距离y(km)与行驶时间x(min)之间的函数图象如图所示,则两船第二次相遇时的地点与B港口相距 km.
18.甲船匀速顺流而下从A港到B港,同时乙船匀速逆流而上从B港到A港,C港处于A、B两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到D处,到D处后迅速按原顺流速度驶向B港,最后甲、乙两船都到达了各自的目的地,甲、乙两船在静水中的速度相同,设甲、乙两船与C港的距离之和为y(km),行驶时间为x(h),y与x的部分关系如图,则当两船在B、C间某处相遇时,两船距离A港的距离为 千米.
三.解答题(共5小题,满分46分)
19.(8分)已知正比例函数y=kx的图象经过第四象限内一点P(k+2,7k+6),求k的值.
20.(8分)如图,直线y=x+b与x轴交于点A,与y轴于点B,点C(﹣2,0)在线段OA上,且OC=OA.
(1)求b的值;
(2)点P是直线y=x+b上一动点,连接PC,PO,求PC+PO的最小值.
21.(9分)甲乙两车间同时开始加工﹣批服装,从开始加工到完成这批服装甲车间工作了8小时,乙车间在中途停工一段时间维修设备,然后在甲车间加工到4小时时按停工前的工作效率继续加工,直至与甲车间同时完成这批服装的加工任务.设甲、乙两车间各自加工服装的数量为y(件),甲车间加工的时间为x(时),y与x的函数图象如图所示.
(1)甲车间每小时加工服装的件数为 件,这批服装的总件数为 件:
(2)乙车间花了多少时间维修设备?
(3)求甲、乙两车间在正常情况下,共同完成加工800件服装时甲车间所用的时间.
22.(9分)2018年8月31日,十三届全国人大常委会第五次会议表决通过全国人大常委会关于修改个人所得税法的决定根据决定,个税“起征点”由3500元/月提高至5000元/月.2019年1月1日起,新版个人所得税税率表正式实施下面是2019最新个人所得税税率表:
级数 月应纳税所得额 税率
1 不超过3000元的部分 3%
2 超过3000至12000元的部分 10%
3 超过12000至25000元的部分 20%
4 超过25000至35000元的部分 25%
5 超过35000至55000元的部分 30%
6 超过55000至80000元的部分 35%
7 超过80000元的部分 45%
月应纳税所得额是指居民个人月工资减去5000元后的余额.
如笑笑的妈妈10月份工资是9000元,则应纳税所得额为9000﹣5000=4000(元),所以笑笑的妈妈应缴纳个人所得税为3000×3%+1000×10%=190(元)
(1)笑笑的表哥10月份工资收人6800元,则他需缴纳的个人所得税是 元;
(2)设笑笑的爸爸10月份工资收人为x元(10000<x≤15000),他10月份需要缴纳的个人所得税为y元,求y与x的函数关系式;
(3)某软件工程师10月份缴纳个人所得税12790元,则他的税前收入是 元.
23.(12分)一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象
(1)李越骑车的速度为 米/分钟;F点的坐标为 ;
(2)求李越从乙地骑往甲地时,s与t之间的函数表达式;
(3)求王明从甲地到乙地时,s与t之间的函数表达式;
(4)求李越与王明第二次相遇时t的值.
答案
一.选择题
B.C.A.A.A.B.C.A.C.C.
二.填空题
11.1.
12.﹣3,3.
13.(2,0)或(2﹣2,0)或(2+2,0).
14.y=4x+8或y=﹣4x﹣8.
15.﹣.
16.
17..
18..
三.解答题
19.解:∵正比例函数y=kx的图象经过点P(k+2,7k+6),
∴7k+6=k(k+2),
整理,得:k2﹣5k﹣6=0,
解得:k1=﹣1,k2=6.
∵点P(k+2,7k+6)在第四象限,
∴,
解得:﹣2<k<﹣,
∴k=﹣1.
∴k的值为﹣1.
20.解:(1)∵点C(﹣2,0)在线段OA上,且OC=OA,
∴OA=3OC=3×2=6,
∴A(﹣6,0),
∵直线y=x+b与x轴交于点A,
∴﹣6+b=0,
∴b=6;
(2)过O作直线AB的对称点O′,连接O′C交AB于点P,此时PC+PO的值最小,最小值为O′C的长,
∵直线为y=x+6,
∴B(0,6),
∴OA=OB=6,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵OO′和AB互相垂直平分,
∴四边形AOBO′是正方形,
∴O′(﹣6,6),
∴O′C==2,
故PC+PO的最小值为2.
21.解:(1)甲车间每小时加工服装件数为720÷8=90(件),
这批服装的总件数为720+390=1110(件).
故答案为:90;1110.
(2)乙车间每小时加工服装件数为:(件),
乙车间维修设备前的工作时间:(时).
乙车间维修设备时间为:4﹣2=2(小时).
答:乙车间花了2时间维修设备;
(3)设乙车间维修设备后y与x的函数关系式为y=kx+b,根据题意得:
,解得,
∴乙车间维修设备后y与x的函数关系式为y=65x﹣130;
由题意可得甲车间加工服装数量y与x之间的函数关系式为y=90x,
设甲,乙两车间共同完成加工服装w件,则:
w=90x+(65x﹣130)=155x﹣130,
当w=800时,155x﹣130=800,
解得x=6,
答:甲、乙两车间在正常情况下,共同完成加工800件服装时甲车间所用的时间为6小时.
22.解:(1)由题意可得,
笑笑的表哥10月份工资收人6800元,则他需缴纳的个人所得税是:(6800﹣5000)×3%=1800×3%=54(元),
故答案为:54;
(2)∵10000<x≤15000,
∴5000<x﹣5000≤10000,
∴y与x的函数关系式为:3000×3%+(x﹣5000﹣3000)×10%=0.1x﹣710,
即y与x的函数关系式为:y=0.1x﹣710;
(3)∵3000×3%=90,
3000×3%+(12000﹣3000)×10%=990,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%=3590,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%+(35000﹣25000)×25%=6090,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%+(35000﹣25000)×25%+(55000﹣35000)×30%=12090,
3000×3%+(12000﹣3000)×10%+(25000﹣12000)×20%+(35000﹣25000)×25%+(55000﹣35000)×30%+(80000﹣55000)×35%=20840,
∵12090<12790<20840,
∴该软件工程师的税前收入在60000~85000之间,
设该软件工程师的税前收入是x元,
12090+(x﹣5000﹣35000)×35%=12790,
解得,x=42000,
故答案为:42000.
23.解:(1)由图象可得,
李越骑车的速度为:2400÷10=240米/分钟,2400÷96=25,所以F点的坐标为(25,0).
故答案为:240;(25,0);
(2)设李越从乙地骑往甲地时,s与t之间的函数表达式为s=kt,
2400=10k,得k=240,
即李越从乙地骑往甲地时,s与t之间的函数表达式为s=240t,
故答案为:s=240t;
(3)设王明从甲地到乙地时,s与t之间的函数表达式为s=kt+2400,根据题意得,
25k+2400=0,
解得k=﹣96,
所以王明从甲地到乙地时,s与t之间的函数表达式为:s=﹣96x+2400;
(4)根据题意得,240(t﹣2)﹣96t=2400,
解得t=20.
答:李越与王明第二次相遇时t的值为20.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
