八年级数学上册试题 第一章 勾股定理 综合复习题-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 第一章 勾股定理 综合复习题-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 645.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 15:33:50 | ||
图片预览




文档简介
第一章 勾股定理 综合复习题
一、单选题
1.如果直角三角形的三边长分别是6、8、,则满足( )
A. B. C.或 D.以上答案都不对
2.某直角三角形的周长为30,且一条直角边长为5,则另一条直角边长为( )
A.3 B.4 C.12 D.13
3.下列各组数是勾股数的是( )
A.3,4,5 B.7,8,9 C.9,41,47 D.52,122,132
4.如图,分别以直角三角形三边为边向外作三个正方形,其面积分别用,、表示,若,,则的值为( ).
A.9 B.12 C.16 D.18
5.下列说法正确的是( ).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
6.如图所示,,为垂足,设,,则,的大小关系为( )
A. B. C. D.不确定
7.利用四个全等的直角三角形可以拼成如图所示的图形通过该图形,可以验证公式( )
A.
B.
C.
D.
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底墙到左墙角的距离为1.5m,顶端距离地面2m,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面0.7m,那么小巷的宽度为( )
A.3.2m B.3.5m C.3.9m D.4m
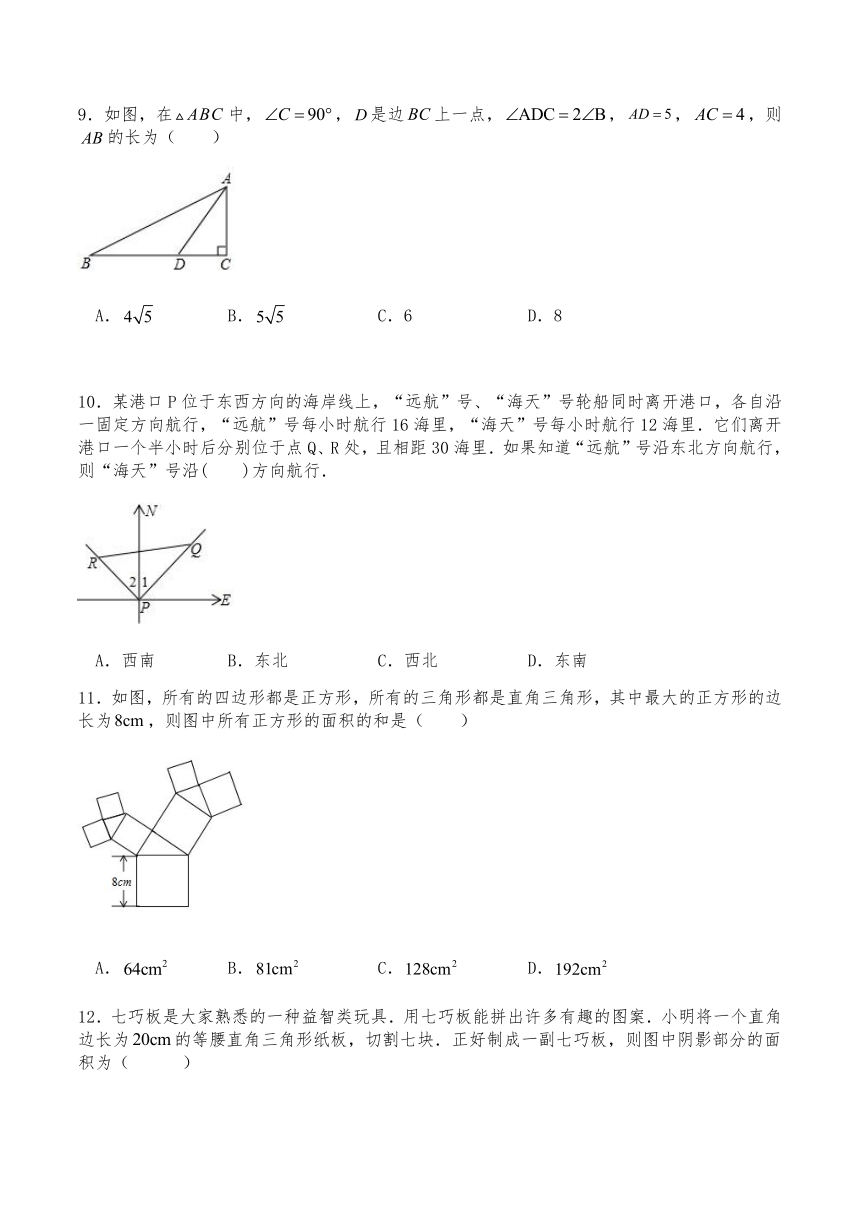
9.如图,在中,,是边上一点,,,,则的长为( )
A. B. C.6 D.8
10.某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q、R处,且相距30海里.如果知道“远航”号沿东北方向航行,则“海天”号沿( )方向航行.
A.西南 B.东北 C.西北 D.东南
11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,则图中所有正方形的面积的和是( )
A. B. C. D.
12.七巧板是大家熟悉的一种益智类玩具.用七巧板能拼出许多有趣的图案.小明将一个直角边长为的等腰直角三角形纸板,切割七块.正好制成一副七巧板,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
13.△ABC三边长分别为2,3,,则△ABC的面积为______.
14.如图,正方形网格中的△ABC,若小方格边长都为1,则△ABC是_____ 三角形.
15.如图,在Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为______.
16.的周长为36 cm,且满足.点从点开始沿边向点以1 cm/s的速度移动,点从点开始沿边向点以2cm/s|的速度移动若两点同时出发,则经过3 s后,的面积为_______.
17.如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处的最短距离为_______(杯壁厚度不计).
18.我国古代数学名著《九章算术》中有云:“今有木长二丈,围之三尺.葛生其下,缠木七周,上与木齐.问葛长几何?”大意为:有一根木头长2丈,上、下底面的周长为3尺,葛生长在木下的一方,绕木7周,葛梢与木头上端刚好齐平,则葛长是______尺.(注:l丈等于10尺,葛缠木以最短的路径向上生长,误差忽略不计)
19.如图是一个长方形零件示意图,已知在长为,宽为的长方形零件上有两个圆孔,与孔中心,的相关数据如图所示.则孔中心间的距离________.
20.四个全等的直角三角形按图示方式围成正方行ABCD,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH,已知AM为Rt△ABM的较长直角边,AM=EF,则正方形ABCD的面积为_______.
21.如图,在中,点、、分别在、、上,且,,,,,则______度.
22.如图,点C为直线l上的一个动点,于D点,于E点,,,当长为________________为直角三角形.
三、解答题
23.如图所示的四边形是张亮家的一块种小麦的田地.经测量边长为30米,边长为40米,边长为120米,边长为130米,,求这块地的面积.
24.如图,在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:.
25.已知在如图的方格中,有一个格点三角形ABC(三个顶点均在格点上),其中,,
(1)请你在方格中画出该三角形;
(2)求的面积;
(3)求中AC边上的高的长(结果保留根号).
26.如图,已知长方体的长,宽,高,一只蚂蚁如果沿长方体的表面从点爬到点,那么沿哪条路最近?最短路程是多少?
27.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
28.在中,,.过点在外作直线,于,于.
(1)证明:;
(2)若,,.试利用此图验证勾股定理.
29.如图,,,,…分别表示各个三角形的面积,仔细观察,并认真分析各式,然后解答问题.
,;
,;
,;
……
(1)用含n(n是正整数)的式子表示和;
(2)若一个三角形的面积是,通过计算说明它是第几个三角形.
30.阅读理解:
(问题情境)
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
(探索新知)
从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积+4个直角三角形的面积.
从而得数学等式:(a+b)2=c2+4×ab,化简证得勾股定理:a2+b2=c2.
(初步运用)
(1)如图1,若b=2a,则小正方形面积:大正方形面积= ;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a=4,b=6,此时空白部分的面积为 ;
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC=3,求该风车状图案的面积.
(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
(迁移运用)
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?
带着这个疑问,小丽拼出图5的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
答案
一、单选题
C.C.A.C.D.C.C.C.A.C.D.B.
二、填空题
13.3.
14.直角
15.2.5.
16.18.
17.
18.29.
19.15
20.32
21.80.
22.3或2或.
三、解答题
23.
连接,由勾股定理得到,根据勾股定理的逆定理得到为直角三角形,再根据三角形面积公式进行计算,即可得到答案.如图,连接.
在中,根据勾股定理是,
得.
在中,
因为,
所以为直角三角形,且.
所以(平方米).
所以这块地的面积为3600平方米.
24.
连接AM得到三个直角三角形,运用勾股定理分别表示出AD 、AM 、BM 进行代换就可以最后得到所要证明的结果.证明:连接MA,
∵MD⊥AB,
∴AD2=AM2-MD2,BM2=BD2+MD2,
∵∠C=90°,
∴AM2=AC2+CM2
∵M为BC中点,
∴BM=MC.
∴AD2=AC2+BD2
25.
(1)根据,,来找出该三角形是三条边,然后顺次连接;
(2)三角形的面积矩形的面积三个小三角形的面积;
(3)由面积法来求中边上的高的长.解:(1)如图,作图(不含;
(2);
(3)如图,过点作于点,则.
26.
要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.如图,
图1
图2 图3
根据题意,如图所示,路径有以下三种情况:
(1)沿,,,,,剪开,得图1,;
(2)沿,,,,,剪开,得图2,;
(3)沿,,,,,剪开,得图3,.
综上所述,最短路径应为图1所示,所以,即,因此最短路程是5cm.
27.过点B作BCAD于C,
所以AC=4﹣2+0.5=2.5m,BC=4.5+1.5=6m,
在直角△ABC中,AB为斜边,则m,
答:机器人从点A到点B之间的距离是m.
考点:勾股定理.
28.
(1)利用已知得出,根据全等三角形的判定可证,进而可得,,即可即可求证;
(2)根据题意利用,,继而即可求证.证明:(1)∵,于,于.
∴,,
∴,
在和中,,
∴(AAS),
∴,,
∴,
即;
(2)∵,
∴,,,
∴,
∵,
,
∴,
∴.
29.
(1)此题要利用直角三角形的面积公式,观察上述结论,会发现,第n个图形的一直角边就是,然后利用面积公式可得.
(2)把三角形的面积代入到(1)的公式即可解答.(1),.
(2)当时,,即,
所以它是第20个三角形.
30.(1)由题意:b=2a,c=,
∴小正方形面积:大正方形面积=5a2:9a2=5:9,
故答案为:5:9;
(2)空白部分的面积为=52﹣2××4×6=28,
故答案为:28;
(3)24÷4=6,
设AC=x,依题意有:(x+3)2+32=(6﹣x)2,
解得x=1,
∴面积为:×(3+1)×3×4
=×4×3×4
=24,
故该飞镖状图案的面积是24;
(4)将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=40,
∴S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=40,
∴x+4y=,
∴S2=x+4y=,
故答案为:;
[迁移运用]结论:a2+b2﹣ab=c2.
理由:由题意:大正三角形面积=三个全等三角形面积+小正三角形面积,
可得:(a+b)×k(a+b)=3××b×ka+×c×ck,
∴(a+b)2=3ab+c2,
∴a2+b2﹣ab=c2.
一、单选题
1.如果直角三角形的三边长分别是6、8、,则满足( )
A. B. C.或 D.以上答案都不对
2.某直角三角形的周长为30,且一条直角边长为5,则另一条直角边长为( )
A.3 B.4 C.12 D.13
3.下列各组数是勾股数的是( )
A.3,4,5 B.7,8,9 C.9,41,47 D.52,122,132
4.如图,分别以直角三角形三边为边向外作三个正方形,其面积分别用,、表示,若,,则的值为( ).
A.9 B.12 C.16 D.18
5.下列说法正确的是( ).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
6.如图所示,,为垂足,设,,则,的大小关系为( )
A. B. C. D.不确定
7.利用四个全等的直角三角形可以拼成如图所示的图形通过该图形,可以验证公式( )
A.
B.
C.
D.
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底墙到左墙角的距离为1.5m,顶端距离地面2m,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面0.7m,那么小巷的宽度为( )
A.3.2m B.3.5m C.3.9m D.4m
9.如图,在中,,是边上一点,,,,则的长为( )
A. B. C.6 D.8
10.某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q、R处,且相距30海里.如果知道“远航”号沿东北方向航行,则“海天”号沿( )方向航行.
A.西南 B.东北 C.西北 D.东南
11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为,则图中所有正方形的面积的和是( )
A. B. C. D.
12.七巧板是大家熟悉的一种益智类玩具.用七巧板能拼出许多有趣的图案.小明将一个直角边长为的等腰直角三角形纸板,切割七块.正好制成一副七巧板,则图中阴影部分的面积为( )
A. B. C. D.
二、填空题
13.△ABC三边长分别为2,3,,则△ABC的面积为______.
14.如图,正方形网格中的△ABC,若小方格边长都为1,则△ABC是_____ 三角形.
15.如图,在Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为______.
16.的周长为36 cm,且满足.点从点开始沿边向点以1 cm/s的速度移动,点从点开始沿边向点以2cm/s|的速度移动若两点同时出发,则经过3 s后,的面积为_______.
17.如图,圆柱形玻璃杯高为,底面周长为,在杯内壁离底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到内壁处的最短距离为_______(杯壁厚度不计).
18.我国古代数学名著《九章算术》中有云:“今有木长二丈,围之三尺.葛生其下,缠木七周,上与木齐.问葛长几何?”大意为:有一根木头长2丈,上、下底面的周长为3尺,葛生长在木下的一方,绕木7周,葛梢与木头上端刚好齐平,则葛长是______尺.(注:l丈等于10尺,葛缠木以最短的路径向上生长,误差忽略不计)
19.如图是一个长方形零件示意图,已知在长为,宽为的长方形零件上有两个圆孔,与孔中心,的相关数据如图所示.则孔中心间的距离________.
20.四个全等的直角三角形按图示方式围成正方行ABCD,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH,已知AM为Rt△ABM的较长直角边,AM=EF,则正方形ABCD的面积为_______.
21.如图,在中,点、、分别在、、上,且,,,,,则______度.
22.如图,点C为直线l上的一个动点,于D点,于E点,,,当长为________________为直角三角形.
三、解答题
23.如图所示的四边形是张亮家的一块种小麦的田地.经测量边长为30米,边长为40米,边长为120米,边长为130米,,求这块地的面积.
24.如图,在△ABC中,∠C=90°,M是BC的中点,MD⊥AB于D,求证:.
25.已知在如图的方格中,有一个格点三角形ABC(三个顶点均在格点上),其中,,
(1)请你在方格中画出该三角形;
(2)求的面积;
(3)求中AC边上的高的长(结果保留根号).
26.如图,已知长方体的长,宽,高,一只蚂蚁如果沿长方体的表面从点爬到点,那么沿哪条路最近?最短路程是多少?
27.中国机器人创意大赛于2014年7月15日在哈尔滨开幕.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从A处先往东走4m,又往北走1.5m,遇到障碍后又往西走2m,再转向北走4.5m处往东一拐,仅走0.5m就到达了B.问机器人从点A到点B之间的距离是多少?
28.在中,,.过点在外作直线,于,于.
(1)证明:;
(2)若,,.试利用此图验证勾股定理.
29.如图,,,,…分别表示各个三角形的面积,仔细观察,并认真分析各式,然后解答问题.
,;
,;
,;
……
(1)用含n(n是正整数)的式子表示和;
(2)若一个三角形的面积是,通过计算说明它是第几个三角形.
30.阅读理解:
(问题情境)
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
(探索新知)
从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积+4个直角三角形的面积.
从而得数学等式:(a+b)2=c2+4×ab,化简证得勾股定理:a2+b2=c2.
(初步运用)
(1)如图1,若b=2a,则小正方形面积:大正方形面积= ;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a=4,b=6,此时空白部分的面积为 ;
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC=3,求该风车状图案的面积.
(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
(迁移运用)
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?
带着这个疑问,小丽拼出图5的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
答案
一、单选题
C.C.A.C.D.C.C.C.A.C.D.B.
二、填空题
13.3.
14.直角
15.2.5.
16.18.
17.
18.29.
19.15
20.32
21.80.
22.3或2或.
三、解答题
23.
连接,由勾股定理得到,根据勾股定理的逆定理得到为直角三角形,再根据三角形面积公式进行计算,即可得到答案.如图,连接.
在中,根据勾股定理是,
得.
在中,
因为,
所以为直角三角形,且.
所以(平方米).
所以这块地的面积为3600平方米.
24.
连接AM得到三个直角三角形,运用勾股定理分别表示出AD 、AM 、BM 进行代换就可以最后得到所要证明的结果.证明:连接MA,
∵MD⊥AB,
∴AD2=AM2-MD2,BM2=BD2+MD2,
∵∠C=90°,
∴AM2=AC2+CM2
∵M为BC中点,
∴BM=MC.
∴AD2=AC2+BD2
25.
(1)根据,,来找出该三角形是三条边,然后顺次连接;
(2)三角形的面积矩形的面积三个小三角形的面积;
(3)由面积法来求中边上的高的长.解:(1)如图,作图(不含;
(2);
(3)如图,过点作于点,则.
26.
要求长方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.如图,
图1
图2 图3
根据题意,如图所示,路径有以下三种情况:
(1)沿,,,,,剪开,得图1,;
(2)沿,,,,,剪开,得图2,;
(3)沿,,,,,剪开,得图3,.
综上所述,最短路径应为图1所示,所以,即,因此最短路程是5cm.
27.过点B作BCAD于C,
所以AC=4﹣2+0.5=2.5m,BC=4.5+1.5=6m,
在直角△ABC中,AB为斜边,则m,
答:机器人从点A到点B之间的距离是m.
考点:勾股定理.
28.
(1)利用已知得出,根据全等三角形的判定可证,进而可得,,即可即可求证;
(2)根据题意利用,,继而即可求证.证明:(1)∵,于,于.
∴,,
∴,
在和中,,
∴(AAS),
∴,,
∴,
即;
(2)∵,
∴,,,
∴,
∵,
,
∴,
∴.
29.
(1)此题要利用直角三角形的面积公式,观察上述结论,会发现,第n个图形的一直角边就是,然后利用面积公式可得.
(2)把三角形的面积代入到(1)的公式即可解答.(1),.
(2)当时,,即,
所以它是第20个三角形.
30.(1)由题意:b=2a,c=,
∴小正方形面积:大正方形面积=5a2:9a2=5:9,
故答案为:5:9;
(2)空白部分的面积为=52﹣2××4×6=28,
故答案为:28;
(3)24÷4=6,
设AC=x,依题意有:(x+3)2+32=(6﹣x)2,
解得x=1,
∴面积为:×(3+1)×3×4
=×4×3×4
=24,
故该飞镖状图案的面积是24;
(4)将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=40,
∴S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=40,
∴x+4y=,
∴S2=x+4y=,
故答案为:;
[迁移运用]结论:a2+b2﹣ab=c2.
理由:由题意:大正三角形面积=三个全等三角形面积+小正三角形面积,
可得:(a+b)×k(a+b)=3××b×ka+×c×ck,
∴(a+b)2=3ab+c2,
∴a2+b2﹣ab=c2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
