七年级数学上册试题 第1章《丰富的图形世界》单元测试-北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 第1章《丰富的图形世界》单元测试-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 525.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 15:47:05 | ||
图片预览

文档简介
第1章《丰富的图形世界》单元测试
一、单选题(每题2分,共24分)
1.下列五种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;其中属于立体图形的是( )
A.①②③ B.③④⑤ C.③⑤ D.④⑤
2.下列几何图形是六棱柱的是( )
A. B. C. D.
3.如图是一个由平面图形绕虚线旋转得到的立体图形,则这个平面图形是( )
A. B. C. D.
4.如图,是一个正方体骰子的表面展开图,将其折叠成正方体骰子(点数朝外),如果1点在上面,3点在左面,在前面的点数为( )
A.2 B.4 C.5 D.6
5.下列图形中是多面体的有( )
A.(1)(2)(4) B.(2)(4)(6) C.(2)(5)(6) D.(1)(3)(5)
6.用一个平面去截一个正方体,如果截去的几何体是一个三棱锥,那么截面一定是( )
A.六边形 B.五方形 C.四边形 D.三角形
7.下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
8.如图是由两块积木搭建的几何体,则该几何体的主视图是( )
A. B. C. D.
9.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:
①可能是锐角三角形; ②可能是直角三角形;
③可能是七边形; ④可能是平行四边形.
其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
10.如图是某几何体的三视图及相关数据,请根据有关信息得这个几何体的全面积是( )
A. B. C. D.
11.一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,则m+n的值为( )
A.17 B.18 C.19 D.20
12.如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A.271 B.272 C.331 D.332
二、填空题(每题2分,共20分)
13.圆柱是由_____个面组成的,其中______个平面,_____个曲面,圆锥是由______个面组成的.
14.如图,三边长分别为的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为_____.(结果保留)
15.五棱柱有___________条棱,有___________个侧面,___________个顶点.
七棱锥有___________条棱,有___________个侧面,___________个顶点.
16.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 ________(填编号).
17.如图,是一个正方体的表面展开图,若正方体相对两个面上的数互为相反数,则3x-y的值为_____.
18.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是________.
19.如图,正方体每个侧面的面积为平方米,用经过,,三点的平面截这个正方体,则所得的切面的周长是________米.
20.用一个平面去截一个正方体,其截面的形状不可能是_________.(请你在“三角形”“四边形”“五边形”“六边形”“七边形”这5种图形中选择符合题意的图形填上即可)
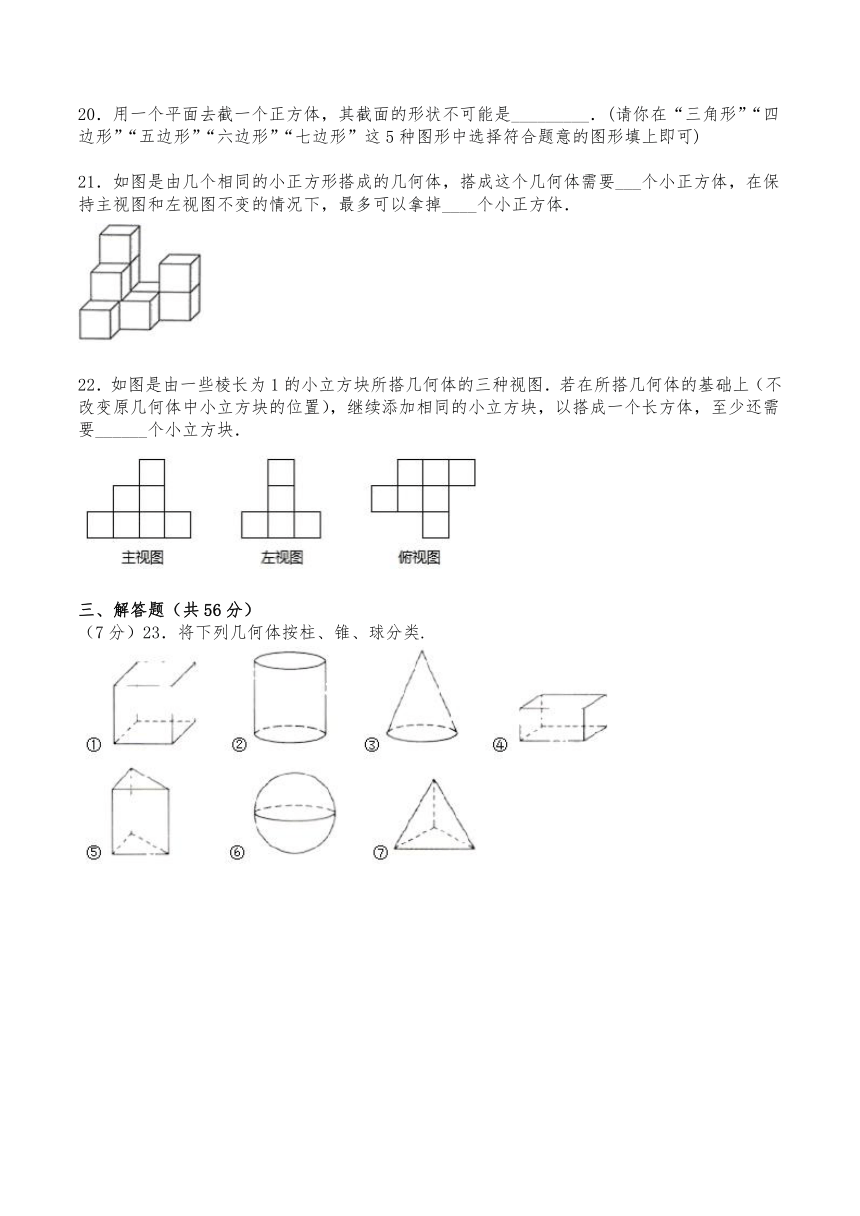
21.如图是由几个相同的小正方形搭成的几何体,搭成这个几何体需要___个小正方体,在保持主视图和左视图不变的情况下,最多可以拿掉____个小正方体.
22.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
三、解答题(共56分)
(7分)23.将下列几何体按柱、锥、球分类.
(7分)24.哥哥花瓶的表面可以看作由哪个平面图形绕虚线旋转一周而得到?用线连一连.
(7分)25.下面截面形状的名称分别是什么?
(1) (2) (3)
(4) (5) (6)
(8分)26.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
(9分)27.如图,是由几个相同小立方块搭成的几何体,从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数.
(1)请画出这个几何体的从正面看和从左面看的形状图.
(2)已知小立方块的棱长为1,求该几何体的表面积.
(9分)28.如图是一个立体图形的展开图,每个面上都标注了数字(图示立体图形的面为立体图形的外表面),请根据要求回答问题:
(1)如果面1在立体图形的顶部,那么哪一面会在下面?
(2)如果面3在前面,从左面看是面2,那么哪一面会在上面?
(3)如果面5在后面,从右面看是面4,那么哪一面会在下面?
(9分)29.某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如图所示,其中阴影部分为内部粘贴角料.(单位:毫米)
(1)此长方体包装盒的体积为 立方毫米;(用含x、y的式子表示)
(2)此长方体的表面积(不含内部粘贴角料)为 平方毫米;(用含x、y的式子表示)
(3)若内部粘贴角料的面积占长方体表面纸板面积的,求当x=40毫米,y=70毫米时,制作这样一个长方体共需要纸板多少平方米.
答案
一、单选题
B.D.B.A.B.D.C.D.B.A.B.C.
二、填空题
13.三 两 一 两
14.
15.15,5,10;14,7,8.
16.3
17.;
18.C
19.
20.七边形
21.10, 1.
22.26
三、解答题
23.
由图形可得①②④⑤为一类,它们都是柱体;③⑦为一类,它们都是锥体;⑥为一类,它是球体.
24.
解:如图所示:
25.
解:
(1)长方形;(2)长方形;(3)长方形;
(4)长方形;(5)三角形;(6)六边形.
26.
解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
27.
解:(1)如图所示:
(2)表面积=(9+5+7+2)×2×12=46.
28.
根据题意和图示:
(1)面3会在下面;(2)面4会在上面;(3)面3会在下面.
29.
解:(1)由题意,知该长方体的长为y毫米,宽为x毫米,高为65毫米,
则长方体包装盒的体积为65xy立方毫米.
故答案为:65xy;
(2)长方体的表面积(不含内部粘贴角料)为:2(xy+65y+65x)立方毫米;
故答案为:2(xy+65y+65x);
(3)∵长方体的长为y毫米,宽为x毫米,高为65毫米,
∴长方体的表面积=2(xy+65y+65x)平方毫米,
又∵内部粘贴角料的面积占长方体表面纸板面积的,
∴制作这样一个长方体共需要纸板的面积=(1+)×2(xy+65y+65x)
=(xy+65y+65x)(平方毫米),
∵x=40,y=70,
∴制作这样一个长方体共需要纸板×(40×70+65×70+65×40)=23216(平方毫米),
23216平方毫米=平方米.
故制作这样一个长方体共需要纸板平方米.
一、单选题(每题2分,共24分)
1.下列五种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;其中属于立体图形的是( )
A.①②③ B.③④⑤ C.③⑤ D.④⑤
2.下列几何图形是六棱柱的是( )
A. B. C. D.
3.如图是一个由平面图形绕虚线旋转得到的立体图形,则这个平面图形是( )
A. B. C. D.
4.如图,是一个正方体骰子的表面展开图,将其折叠成正方体骰子(点数朝外),如果1点在上面,3点在左面,在前面的点数为( )
A.2 B.4 C.5 D.6
5.下列图形中是多面体的有( )
A.(1)(2)(4) B.(2)(4)(6) C.(2)(5)(6) D.(1)(3)(5)
6.用一个平面去截一个正方体,如果截去的几何体是一个三棱锥,那么截面一定是( )
A.六边形 B.五方形 C.四边形 D.三角形
7.下列图形是正方体展开图的个数为( )
A.1个 B.2个 C.3个 D.4个
8.如图是由两块积木搭建的几何体,则该几何体的主视图是( )
A. B. C. D.
9.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:
①可能是锐角三角形; ②可能是直角三角形;
③可能是七边形; ④可能是平行四边形.
其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
10.如图是某几何体的三视图及相关数据,请根据有关信息得这个几何体的全面积是( )
A. B. C. D.
11.一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,则m+n的值为( )
A.17 B.18 C.19 D.20
12.如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A.271 B.272 C.331 D.332
二、填空题(每题2分,共20分)
13.圆柱是由_____个面组成的,其中______个平面,_____个曲面,圆锥是由______个面组成的.
14.如图,三边长分别为的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为_____.(结果保留)
15.五棱柱有___________条棱,有___________个侧面,___________个顶点.
七棱锥有___________条棱,有___________个侧面,___________个顶点.
16.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1、2、3、6的小正方形中不能剪去的是 ________(填编号).
17.如图,是一个正方体的表面展开图,若正方体相对两个面上的数互为相反数,则3x-y的值为_____.
18.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是________.
19.如图,正方体每个侧面的面积为平方米,用经过,,三点的平面截这个正方体,则所得的切面的周长是________米.
20.用一个平面去截一个正方体,其截面的形状不可能是_________.(请你在“三角形”“四边形”“五边形”“六边形”“七边形”这5种图形中选择符合题意的图形填上即可)
21.如图是由几个相同的小正方形搭成的几何体,搭成这个几何体需要___个小正方体,在保持主视图和左视图不变的情况下,最多可以拿掉____个小正方体.
22.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
三、解答题(共56分)
(7分)23.将下列几何体按柱、锥、球分类.
(7分)24.哥哥花瓶的表面可以看作由哪个平面图形绕虚线旋转一周而得到?用线连一连.
(7分)25.下面截面形状的名称分别是什么?
(1) (2) (3)
(4) (5) (6)
(8分)26.下面是一个多面体的表面展开图每个面上都标注了字母,(所有字母都写在这一多面体的外表面)请根据要求回答问题:
(1)如果面在前面,从左边看是,那么哪一面会在上面?
(2)如果从右面看是面面,面在后边那么哪一面会在上面?
(3)如果面在多面体的底部,从右边看是,那么哪一面会在前面.
(9分)27.如图,是由几个相同小立方块搭成的几何体,从上面看的形状图,小正方形中的数字表示在该位置的小立方块的个数.
(1)请画出这个几何体的从正面看和从左面看的形状图.
(2)已知小立方块的棱长为1,求该几何体的表面积.
(9分)28.如图是一个立体图形的展开图,每个面上都标注了数字(图示立体图形的面为立体图形的外表面),请根据要求回答问题:
(1)如果面1在立体图形的顶部,那么哪一面会在下面?
(2)如果面3在前面,从左面看是面2,那么哪一面会在上面?
(3)如果面5在后面,从右面看是面4,那么哪一面会在下面?
(9分)29.某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如图所示,其中阴影部分为内部粘贴角料.(单位:毫米)
(1)此长方体包装盒的体积为 立方毫米;(用含x、y的式子表示)
(2)此长方体的表面积(不含内部粘贴角料)为 平方毫米;(用含x、y的式子表示)
(3)若内部粘贴角料的面积占长方体表面纸板面积的,求当x=40毫米,y=70毫米时,制作这样一个长方体共需要纸板多少平方米.
答案
一、单选题
B.D.B.A.B.D.C.D.B.A.B.C.
二、填空题
13.三 两 一 两
14.
15.15,5,10;14,7,8.
16.3
17.;
18.C
19.
20.七边形
21.10, 1.
22.26
三、解答题
23.
由图形可得①②④⑤为一类,它们都是柱体;③⑦为一类,它们都是锥体;⑥为一类,它是球体.
24.
解:如图所示:
25.
解:
(1)长方形;(2)长方形;(3)长方形;
(4)长方形;(5)三角形;(6)六边形.
26.
解:(1)由图可知,如果F面在前面,B面在左面,那么“E”面下面,∵面“C”与面“E”相对,∴C面会在上面;
(2)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,∵面“A”与面“F”相对,∴A面在上面.
(3)由图可知,如果面在多面体的底部,从右边看是,那么“E”面在后面,∵面“C”与面“E”相对,∴ 面会在前面
27.
解:(1)如图所示:
(2)表面积=(9+5+7+2)×2×12=46.
28.
根据题意和图示:
(1)面3会在下面;(2)面4会在上面;(3)面3会在下面.
29.
解:(1)由题意,知该长方体的长为y毫米,宽为x毫米,高为65毫米,
则长方体包装盒的体积为65xy立方毫米.
故答案为:65xy;
(2)长方体的表面积(不含内部粘贴角料)为:2(xy+65y+65x)立方毫米;
故答案为:2(xy+65y+65x);
(3)∵长方体的长为y毫米,宽为x毫米,高为65毫米,
∴长方体的表面积=2(xy+65y+65x)平方毫米,
又∵内部粘贴角料的面积占长方体表面纸板面积的,
∴制作这样一个长方体共需要纸板的面积=(1+)×2(xy+65y+65x)
=(xy+65y+65x)(平方毫米),
∵x=40,y=70,
∴制作这样一个长方体共需要纸板×(40×70+65×70+65×40)=23216(平方毫米),
23216平方毫米=平方米.
故制作这样一个长方体共需要纸板平方米.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
