2023秋人教版六年级数学上册 比的基本性质(课件)(共12张PPT)
文档属性
| 名称 | 2023秋人教版六年级数学上册 比的基本性质(课件)(共12张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 00:00:00 | ||
图片预览




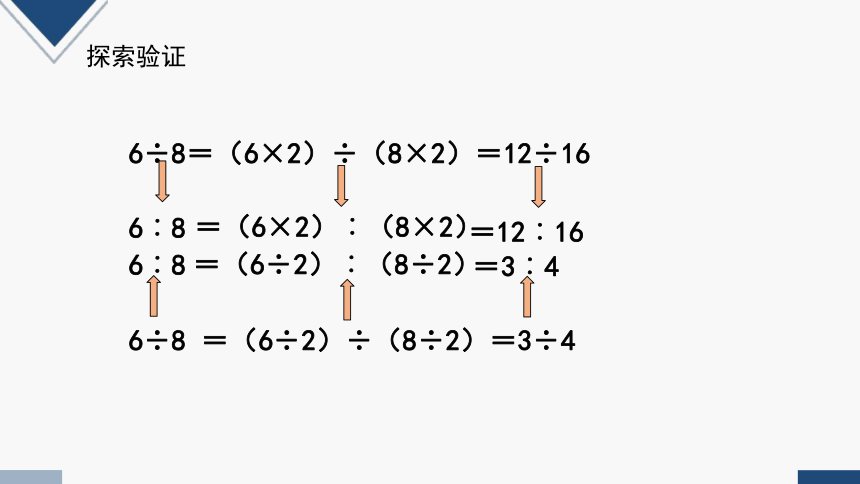
文档简介
(共12张PPT)
2023秋 人教数学
六年级上册
比的基本性质
情景导入
小巴、小亮、小宏都喜欢制作折纸。有一天,他们三人在争论谁每分钟折的纸飞机数多?
小巴说:“我折的纸飞机数与时间(分)的比是6︰8。”
小亮说:“我折的纸飞机数与时间(分)的比是3︰4。”
小宏说:“我折的纸飞机数与时间(分)的比是12︰16。”
6︰8=6÷8 = =
8
6
4
3
小巴:
小亮:
小宏:
问题:小巴、小亮、小宏谁折得快?
3︰4= 3÷4 =
12︰16=12÷16= =
4
3
3
4
16
12
观察猜想
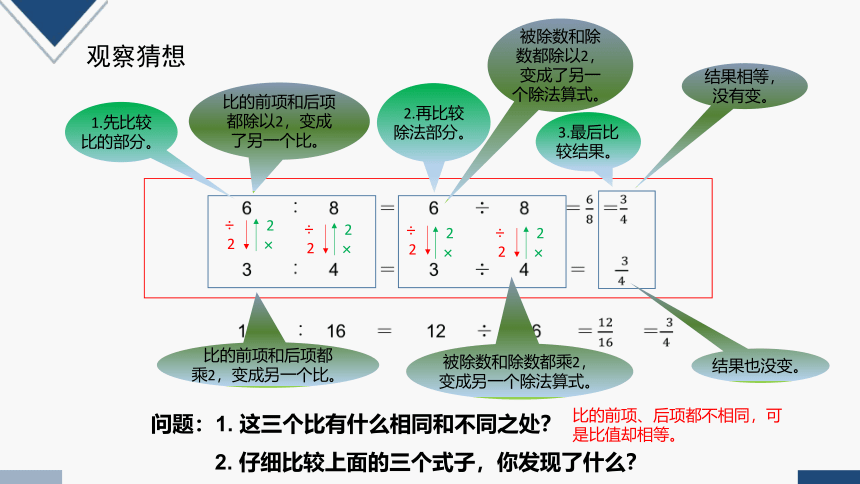
问题:1. 这三个比有什么相同和不同之处?
2. 仔细比较上面的三个式子,你发现了什么?
比的前项、后项都不相同,可是比值却相等。
÷
2
÷
2
1.先比较比的部分。
2.再比较除法部分。
÷
2
÷
2
比的前项和后项都除以2,变成了另一个比。
被除数和除数都除以2,变成了另一个除法算式。
3.最后比较结果。
结果相等, 没有变。
2
×
2
×
比的前项和后项都乘2,变成另一个比。
2
×
2
×
被除数和除数都乘2,变成另一个除法算式。
结果也没变。
观察猜想
比的前项和后项同时乘或除以相同的数,比值不变。
探索验证
6÷8=(6×2)÷(8×2)=12÷16
6÷8 =(6÷2)÷(8÷2)=3÷4
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
探索验证
商不变规律中把0排除在外,那研究比的时候呢?如果把前项后项同时乘以“0”,会怎么样呢?
探索验证
比的前项和后项同时乘或除以相同的数(0除外),比值不变
这叫做比的基本性质。
运用
判断并说明理由。
(1)6︰7=(6×0)︰(7×0)=0
(2)1︰2=(1+2)︰(2+2)=0.75
(3)2︰8=2︰(8÷2)=0.5
(4)3︰5=(3×2)︰(5×2)=0.6
问题:你觉得上面的做法正确吗?如果错误,错在哪里?
×
×
×
上面的做法(1)(2)(3)都不正确,没有根据比的基本性质。
√
只有(4)是正确的,遵循了比的基本性质。
拓展
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
你知道吗?
请你自己收集一些有关黄金比的信息与同学交流。
ɑ︰b≈0.618︰1
小结
比的前项和后项同时乘或除以相同的数(0除外),比值不变这叫做比的基本性质。
猜想——验证——运用
谢谢观看
2023秋 人教数学
六年级上册
比的基本性质
情景导入
小巴、小亮、小宏都喜欢制作折纸。有一天,他们三人在争论谁每分钟折的纸飞机数多?
小巴说:“我折的纸飞机数与时间(分)的比是6︰8。”
小亮说:“我折的纸飞机数与时间(分)的比是3︰4。”
小宏说:“我折的纸飞机数与时间(分)的比是12︰16。”
6︰8=6÷8 = =
8
6
4
3
小巴:
小亮:
小宏:
问题:小巴、小亮、小宏谁折得快?
3︰4= 3÷4 =
12︰16=12÷16= =
4
3
3
4
16
12
观察猜想
问题:1. 这三个比有什么相同和不同之处?
2. 仔细比较上面的三个式子,你发现了什么?
比的前项、后项都不相同,可是比值却相等。
÷
2
÷
2
1.先比较比的部分。
2.再比较除法部分。
÷
2
÷
2
比的前项和后项都除以2,变成了另一个比。
被除数和除数都除以2,变成了另一个除法算式。
3.最后比较结果。
结果相等, 没有变。
2
×
2
×
比的前项和后项都乘2,变成另一个比。
2
×
2
×
被除数和除数都乘2,变成另一个除法算式。
结果也没变。
观察猜想
比的前项和后项同时乘或除以相同的数,比值不变。
探索验证
6÷8=(6×2)÷(8×2)=12÷16
6÷8 =(6÷2)÷(8÷2)=3÷4
6︰8
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
探索验证
商不变规律中把0排除在外,那研究比的时候呢?如果把前项后项同时乘以“0”,会怎么样呢?
探索验证
比的前项和后项同时乘或除以相同的数(0除外),比值不变
这叫做比的基本性质。
运用
判断并说明理由。
(1)6︰7=(6×0)︰(7×0)=0
(2)1︰2=(1+2)︰(2+2)=0.75
(3)2︰8=2︰(8÷2)=0.5
(4)3︰5=(3×2)︰(5×2)=0.6
问题:你觉得上面的做法正确吗?如果错误,错在哪里?
×
×
×
上面的做法(1)(2)(3)都不正确,没有根据比的基本性质。
√
只有(4)是正确的,遵循了比的基本性质。
拓展
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
你知道吗?
请你自己收集一些有关黄金比的信息与同学交流。
ɑ︰b≈0.618︰1
小结
比的前项和后项同时乘或除以相同的数(0除外),比值不变这叫做比的基本性质。
猜想——验证——运用
谢谢观看
