三线八角:同位角、内错角、同旁内角[下学期]
文档属性
| 名称 | 三线八角:同位角、内错角、同旁内角[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 535.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-17 00:00:00 | ||
图片预览



文档简介
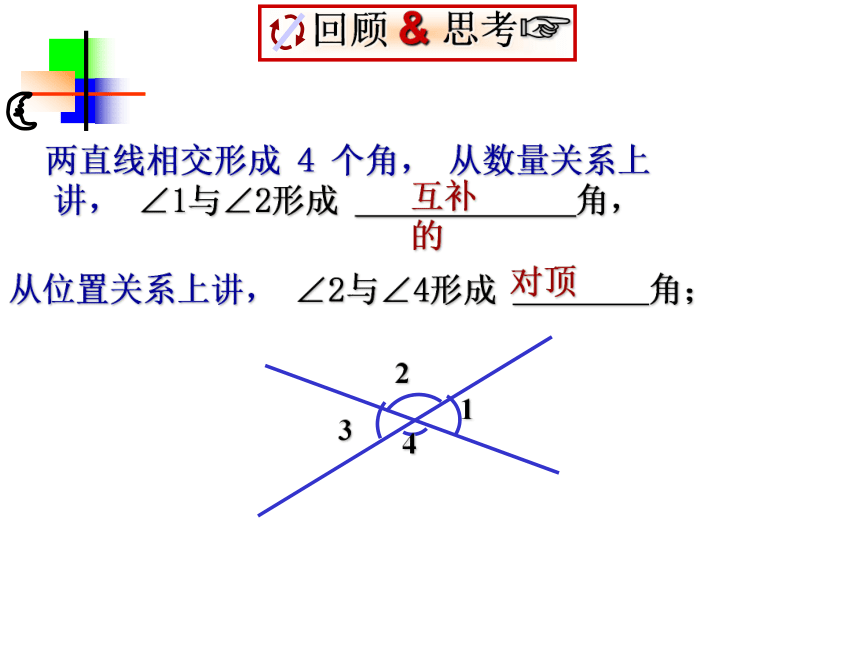
课件26张PPT。(补充课题)三线八角:同位角、内错角、同旁内角回顾与思考1234互补的从位置关系上讲, ∠2与∠4形成 角;对顶两直线相交形成 4 个角, 从数量关系上讲, ∠1与∠2形成 角,构成的八个角中, 两直线被第三直线所截, ①位于两直线同一方、 ② 位于两直线的 ,
且在第三直线的 的
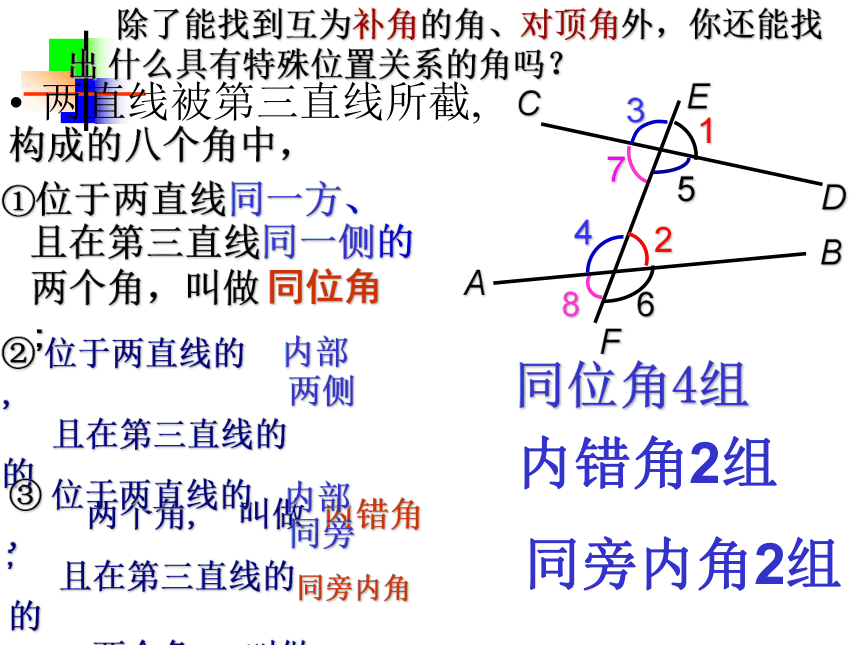
两个角, 叫做 内错角 ; 且在第三直线同一侧的
两个角,叫做 ; 同位角内部两侧③ 位于两直线的 ,
且在第三直线的 的
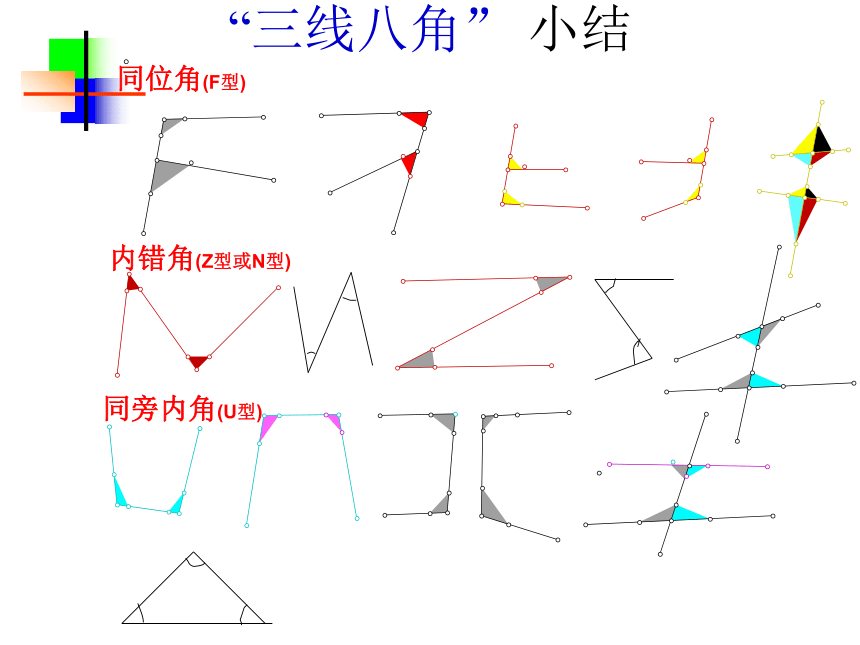
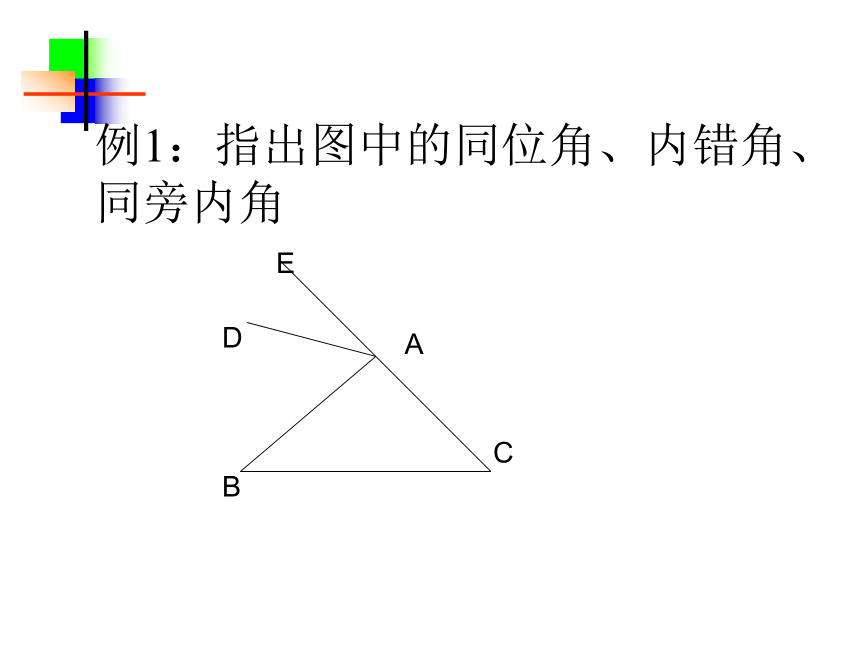
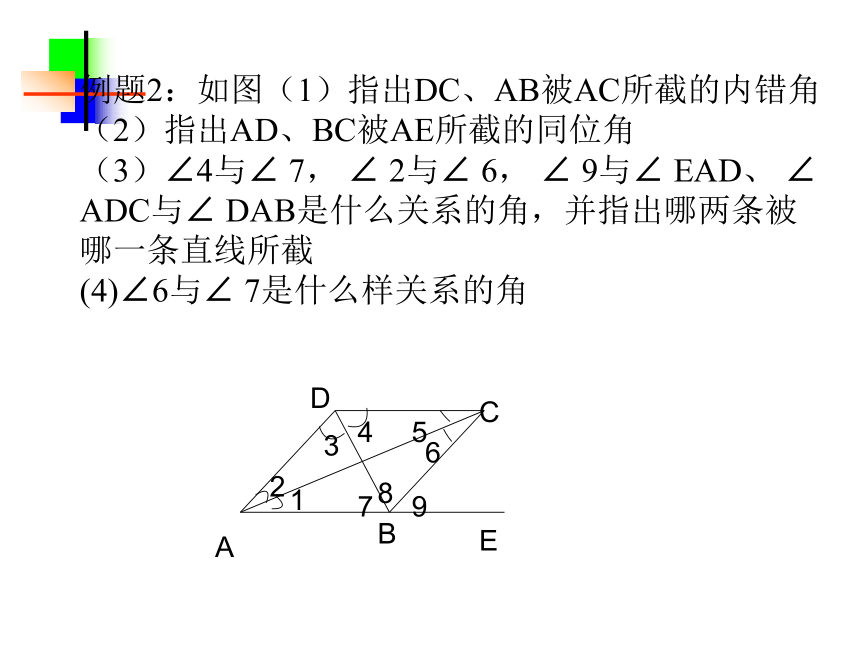
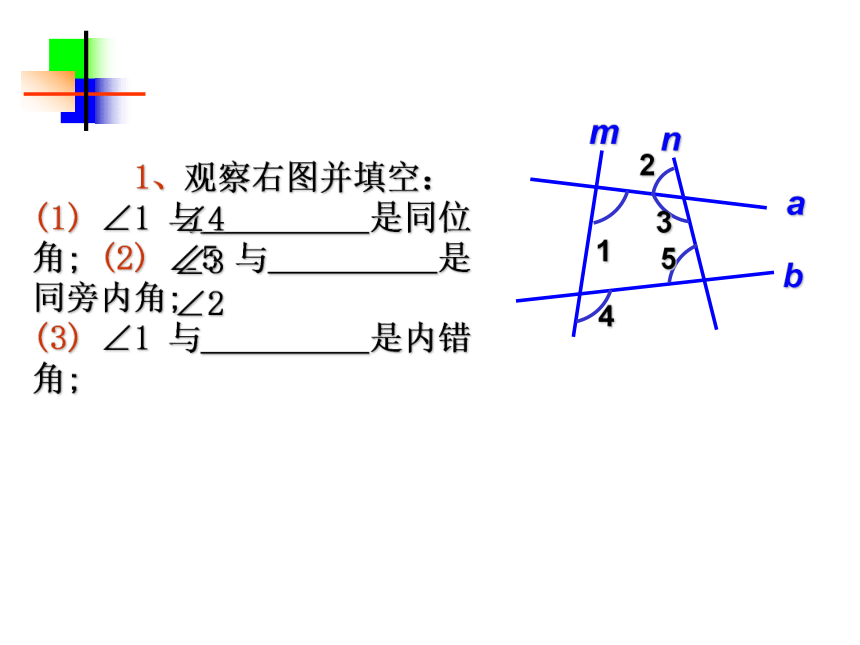
两个角, 叫做; 内部同旁 除了能找到互为补角的角、对顶角外,你还能找出 什么具有特殊位置关系的角吗?同位角4组内错角2组同旁内角2组同旁内角 (1)同位角、内错角、同旁内角都是指两个的位置关系,它们与对顶角、邻补角一样,都是成对出现 同位角的位置特征 (1)在截线的两旁(2)被截的两条直线的同方向 内错角的位置特征 (1)在截线的两旁(2)被截的两条直线之间 同旁内角的位置特征 (1)在截线的同旁(2)被截的两条直线之间 在辩别这些角之前,先弄清哪两条直线被第三条直线所截注意:特殊情况同位角(F型)内错角(Z型或N型)同旁内角(U型)“三线八角” 小结例1:指出图中的同位角、内错角、同旁内角例题2:如图(1)指出DC、AB被AC所截的内错角 (2)指出AD、BC被AE所截的同位角 (3)∠4与∠ 7, ∠ 2与∠ 6, ∠ 9与∠ EAD、 ∠ ADC与∠ DAB是什么关系的角,并指出哪两条被哪一条直线所截 (4)∠6与∠ 7是什么样关系的角 1、观察右图并填空:
(1) ∠1 与 是同位角; (2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角; banm23145∠4∠3∠2练习2(1)如图, ∠ 1与∠ 2是内错角,是由直线___与____被____所截构成
(2)如图,下列说法正确的是( )
(A)1与4是同位角 (B)1与3是同位角
(C)2与4是同位角(D)2与3是同位角小结 作业:另补 如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1=∠2时①直线a和b不平行②直线a∥b③直线a和b不平行做一做判断两条直线平行的方法:两直线平行的判断不平行∥不平行由此可得:两直线 平行的公理同位∴ a ∥b。∵同位角相等,两直线平行,∠1和∠2同位角,相等,48.5° 如何判断两条直线平行21 48.5° 你还记得怎样用移动三角尺的方法画两
条平行线吗?同位角相等,两直线平行.一、放二、靠三、推四、画请说出其中的道理。 已知直线外一点画它的平行线 1、找出下面点阵图中互相平行的线段,
并说明理由(点阵中相邻的四个点构成正方形)① AB∥CD.② EF∥GH.∵ ∠AMP=∠CPF=45°∴ AB∥CD.∵ ∠AMP=∠ANQ=45°,∴ EF∥GH.EGBDFH请看下面的推理是否正确∵ ∠AMP=∠CQH∴ EF∥GH。ACMNPQ(同位角相等,两直线平行)(同位角相等,两直线平行) 2、如图,∠1 = ∠2 = 55°, ∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。第2题图312ABFCDE∵ ∠1 = ∠2 = 55° ∠3 = ∠2, ∴ ∠3 =∠1= 55° ∴ AB∥CD. 随堂练习p55( )对顶角相等(同位角相等,两直线平行)在下图中,满足什么条件,直线AB//CD?F13752486DCABE当∠1=∠2或∠5=∠6,
或∠3=∠4或∠7=∠8时,AB//CD理由:同位角相等,两直线平行∵ ∠1=∠2∠1=∠7∴ ∠2=∠7即:同位角角相等时,内错角也相等为什么“内错角相等时,二直线平行”已知: 如图 , 二直线a 、 bba被第三直线 c 所截,求证: 直线 a∥b.内错角 ∠1 = ∠2 . 证明: 设∠1 的对顶角是∠3, ∵∠3 = ∠1, ( )对顶角相等∵ ∠1 = ∠2, ( ) 已知∴ ∠3 = ∠2; ( )∴ 直线 a∥b. ( ). 等量代换同位角相等,两直线平行.同位角相等对顶角相等内错角相等为什么“同旁内角互补时,二直线平行”已知: 如图 , 二直线a 、 bba被第三直线 c 所截,求证: 直线 a∥b.同旁内角 ∠1 与∠2互补 . 证明: 设∠1 的 角是∠3, 已知∴ 直线 a∥b. ( ). 同位角相等 同旁内角互补1补互补内错角相等同角的补角
相等∵ ∠1 、 ∠2 , ( ) ∴ ∠3 ; ( )= ∠2同角的补角相等内错角相等,两直线平行.平行线的判定1、∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
2、∵∠2=∠3 (已知)
∴a∥b
(内错角相等,两直线平行)
3、∵∠2+∠3=180° (已知)
∴a∥b
(同旁内角互补,两直线平行)
二直线平行 的 判定ba4 考察两直线是否有平行关系,我们往往用第三直线作为沟通这两直线的桥梁—— 考察(被第三直线截成的八个角中)不共顶点的两个角, 是否满足某种数量关系 . 如图2—8,三个相
同的三角尺拼成一个图
形,请找出图中的一组
平行线,并说明你的理由。a∥b.l∥m.l∥n .ABCDE本节课你的收获是什么?本节课你学到了什么?两条直线被第三条直线所截 习题:典中典。作业回顾与思考不在同一平面内——在同一平面内异面直线相交平行同一平面内,不相交同一平面内(无公共点)——(1)同一平面内;(2) 没有交点.
且在第三直线的 的
两个角, 叫做 内错角 ; 且在第三直线同一侧的
两个角,叫做 ; 同位角内部两侧③ 位于两直线的 ,
且在第三直线的 的
两个角, 叫做; 内部同旁 除了能找到互为补角的角、对顶角外,你还能找出 什么具有特殊位置关系的角吗?同位角4组内错角2组同旁内角2组同旁内角 (1)同位角、内错角、同旁内角都是指两个的位置关系,它们与对顶角、邻补角一样,都是成对出现 同位角的位置特征 (1)在截线的两旁(2)被截的两条直线的同方向 内错角的位置特征 (1)在截线的两旁(2)被截的两条直线之间 同旁内角的位置特征 (1)在截线的同旁(2)被截的两条直线之间 在辩别这些角之前,先弄清哪两条直线被第三条直线所截注意:特殊情况同位角(F型)内错角(Z型或N型)同旁内角(U型)“三线八角” 小结例1:指出图中的同位角、内错角、同旁内角例题2:如图(1)指出DC、AB被AC所截的内错角 (2)指出AD、BC被AE所截的同位角 (3)∠4与∠ 7, ∠ 2与∠ 6, ∠ 9与∠ EAD、 ∠ ADC与∠ DAB是什么关系的角,并指出哪两条被哪一条直线所截 (4)∠6与∠ 7是什么样关系的角 1、观察右图并填空:
(1) ∠1 与 是同位角; (2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角; banm23145∠4∠3∠2练习2(1)如图, ∠ 1与∠ 2是内错角,是由直线___与____被____所截构成
(2)如图,下列说法正确的是( )
(A)1与4是同位角 (B)1与3是同位角
(C)2与4是同位角(D)2与3是同位角小结 作业:另补 如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1=∠2时①直线a和b不平行②直线a∥b③直线a和b不平行做一做判断两条直线平行的方法:两直线平行的判断不平行∥不平行由此可得:两直线 平行的公理同位∴ a ∥b。∵同位角相等,两直线平行,∠1和∠2同位角,相等,48.5° 如何判断两条直线平行21 48.5° 你还记得怎样用移动三角尺的方法画两
条平行线吗?同位角相等,两直线平行.一、放二、靠三、推四、画请说出其中的道理。 已知直线外一点画它的平行线 1、找出下面点阵图中互相平行的线段,
并说明理由(点阵中相邻的四个点构成正方形)① AB∥CD.② EF∥GH.∵ ∠AMP=∠CPF=45°∴ AB∥CD.∵ ∠AMP=∠ANQ=45°,∴ EF∥GH.EGBDFH请看下面的推理是否正确∵ ∠AMP=∠CQH∴ EF∥GH。ACMNPQ(同位角相等,两直线平行)(同位角相等,两直线平行) 2、如图,∠1 = ∠2 = 55°, ∠3等于多少度?
直线AB、CD平行吗? 说明你的理由。第2题图312ABFCDE∵ ∠1 = ∠2 = 55° ∠3 = ∠2, ∴ ∠3 =∠1= 55° ∴ AB∥CD. 随堂练习p55( )对顶角相等(同位角相等,两直线平行)在下图中,满足什么条件,直线AB//CD?F13752486DCABE当∠1=∠2或∠5=∠6,
或∠3=∠4或∠7=∠8时,AB//CD理由:同位角相等,两直线平行∵ ∠1=∠2∠1=∠7∴ ∠2=∠7即:同位角角相等时,内错角也相等为什么“内错角相等时,二直线平行”已知: 如图 , 二直线a 、 bba被第三直线 c 所截,求证: 直线 a∥b.内错角 ∠1 = ∠2 . 证明: 设∠1 的对顶角是∠3, ∵∠3 = ∠1, ( )对顶角相等∵ ∠1 = ∠2, ( ) 已知∴ ∠3 = ∠2; ( )∴ 直线 a∥b. ( ). 等量代换同位角相等,两直线平行.同位角相等对顶角相等内错角相等为什么“同旁内角互补时,二直线平行”已知: 如图 , 二直线a 、 bba被第三直线 c 所截,求证: 直线 a∥b.同旁内角 ∠1 与∠2互补 . 证明: 设∠1 的 角是∠3, 已知∴ 直线 a∥b. ( ). 同位角相等 同旁内角互补1补互补内错角相等同角的补角
相等∵ ∠1 、 ∠2 , ( ) ∴ ∠3 ; ( )= ∠2同角的补角相等内错角相等,两直线平行.平行线的判定1、∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
2、∵∠2=∠3 (已知)
∴a∥b
(内错角相等,两直线平行)
3、∵∠2+∠3=180° (已知)
∴a∥b
(同旁内角互补,两直线平行)
二直线平行 的 判定ba4 考察两直线是否有平行关系,我们往往用第三直线作为沟通这两直线的桥梁—— 考察(被第三直线截成的八个角中)不共顶点的两个角, 是否满足某种数量关系 . 如图2—8,三个相
同的三角尺拼成一个图
形,请找出图中的一组
平行线,并说明你的理由。a∥b.l∥m.l∥n .ABCDE本节课你的收获是什么?本节课你学到了什么?两条直线被第三条直线所截 习题:典中典。作业回顾与思考不在同一平面内——在同一平面内异面直线相交平行同一平面内,不相交同一平面内(无公共点)——(1)同一平面内;(2) 没有交点.
