3.4.1 函数与方程(1)函数的零点
文档属性
| 名称 | 3.4.1 函数与方程(1)函数的零点 |

|
|
| 格式 | zip | ||
| 文件大小 | 672.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-10 00:00:00 | ||
图片预览





文档简介
课件19张PPT。3.4.1 函数与方程方程解法史话方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
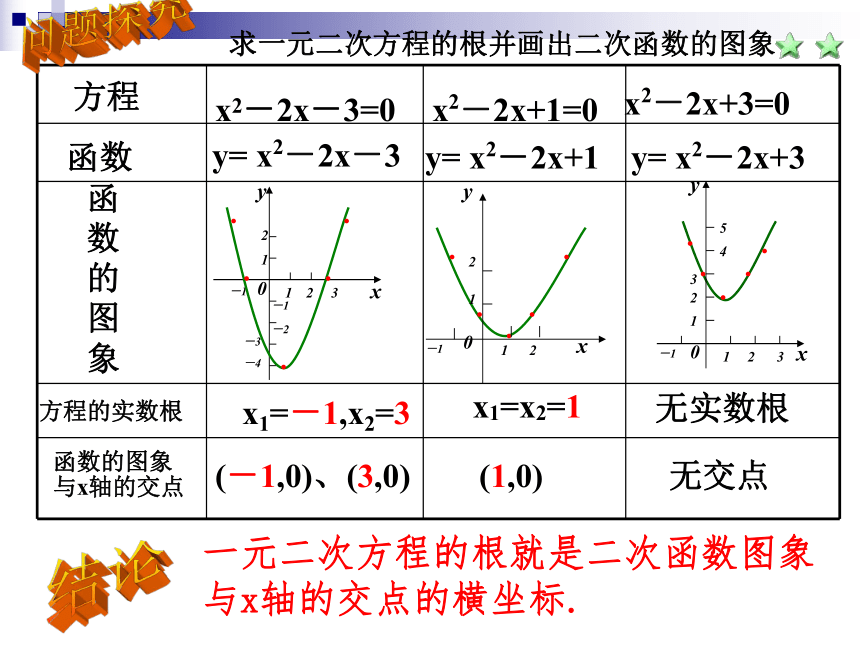
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3求一元二次方程的根并画出二次函数的图象一元二次方程的根就是二次函数图象与x轴的交点的横坐标.
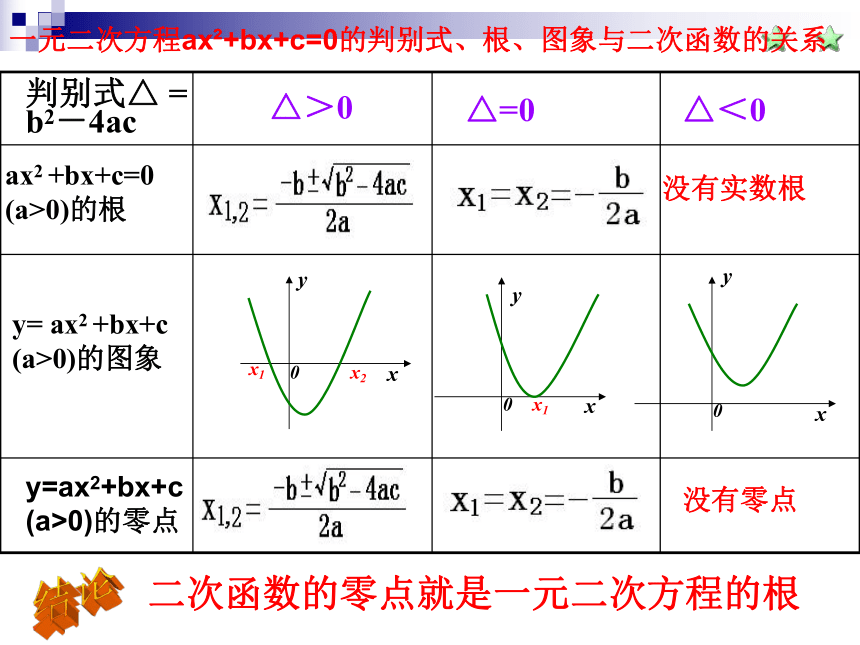
问题探究结论ax2 +bx+c=0
(a>0)的根y= ax2 +bx+c
(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0y=ax2+bx+c
(a>0)的零点没有实数根没有零点二次函数的零点就是一元二次方程的根结论一元二次方程ax2+bx+c=0的判别式、根、图象与二次函数的关系 一般地,我们把使函数y=f(x)的值为0的实数x称为函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数;新知理解①从“数”看:函数y=?(x)的零点就
是方程?(x)=0的实数根;
②从“形”看:函数y=?(x)的零点就
是它的图象与x轴交点的横坐标.求出下列函数的零点:
(1)y=2x+3; (2)y=x2-4x;
(3)y=-3x2-9; (4)y=x2-3x+2.课堂练习一例1求证:二次函数y=2x2+3x-7有 两个不同的零点;并求出零点. 问题解决:解析:令y=0时,2x2+3x-7=0,
∵△=32-4×2×(-7)=65>0,
∴方程有两个不相等的实数根,
因此,二次函数y=2x2+3x-7有
两个不同的零点.其零点为:
2.证明:函数y=x2+6x+4有两个不同的零点.针对性练习证明:
令y=0时,x2+6x+4=0,
∵△=62-4×4=20>0,
∴方程有两个不相等的实数根,
∴函数y=x2+6x+4有两个不同的零点.观察下面函数图象思考:虽然函数f(x) 满足了f(-1)f(1)<0,但它在区间(-1,1)上却没有零点,为什么?观察与探究若函数y=f(x)满足f(a)f(b)<0,那么函数在(a,b)有零点吗?为什么?观察与反思例2:判断函数y=x2-2x-1 在区间(2,3)上是否存在零点?f(2)=-1<0,f(3)=2>0在(2,3)存在零点新知理解新知理解若函数y=f(x)在(a,b)有零点能得到f(a)f(b)<0吗?观察与反思例题: 问题解决4.判断函数f(x)=2x+x-4在区间(1,2)上是否
有零点?练习5.函数零点的定义小结与思考:等价关系:几种常见基本初等函数的零点(1)正比例函数y=kx(k≠0)的零点为0.
课外作业
P93 练习:1、5
P97 习题:1
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3求一元二次方程的根并画出二次函数的图象一元二次方程的根就是二次函数图象与x轴的交点的横坐标.
问题探究结论ax2 +bx+c=0
(a>0)的根y= ax2 +bx+c
(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0y=ax2+bx+c
(a>0)的零点没有实数根没有零点二次函数的零点就是一元二次方程的根结论一元二次方程ax2+bx+c=0的判别式、根、图象与二次函数的关系 一般地,我们把使函数y=f(x)的值为0的实数x称为函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数;新知理解①从“数”看:函数y=?(x)的零点就
是方程?(x)=0的实数根;
②从“形”看:函数y=?(x)的零点就
是它的图象与x轴交点的横坐标.求出下列函数的零点:
(1)y=2x+3; (2)y=x2-4x;
(3)y=-3x2-9; (4)y=x2-3x+2.课堂练习一例1求证:二次函数y=2x2+3x-7有 两个不同的零点;并求出零点. 问题解决:解析:令y=0时,2x2+3x-7=0,
∵△=32-4×2×(-7)=65>0,
∴方程有两个不相等的实数根,
因此,二次函数y=2x2+3x-7有
两个不同的零点.其零点为:
2.证明:函数y=x2+6x+4有两个不同的零点.针对性练习证明:
令y=0时,x2+6x+4=0,
∵△=62-4×4=20>0,
∴方程有两个不相等的实数根,
∴函数y=x2+6x+4有两个不同的零点.观察下面函数图象思考:虽然函数f(x) 满足了f(-1)f(1)<0,但它在区间(-1,1)上却没有零点,为什么?观察与探究若函数y=f(x)满足f(a)f(b)<0,那么函数在(a,b)有零点吗?为什么?观察与反思例2:判断函数y=x2-2x-1 在区间(2,3)上是否存在零点?f(2)=-1<0,f(3)=2>0在(2,3)存在零点新知理解新知理解若函数y=f(x)在(a,b)有零点能得到f(a)f(b)<0吗?观察与反思例题: 问题解决4.判断函数f(x)=2x+x-4在区间(1,2)上是否
有零点?练习5.函数零点的定义小结与思考:等价关系:几种常见基本初等函数的零点(1)正比例函数y=kx(k≠0)的零点为0.
课外作业
P93 练习:1、5
P97 习题:1
