直线平行的条件[下学期]
文档属性
| 名称 | 直线平行的条件[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 578.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-22 20:25:00 | ||
图片预览



文档简介
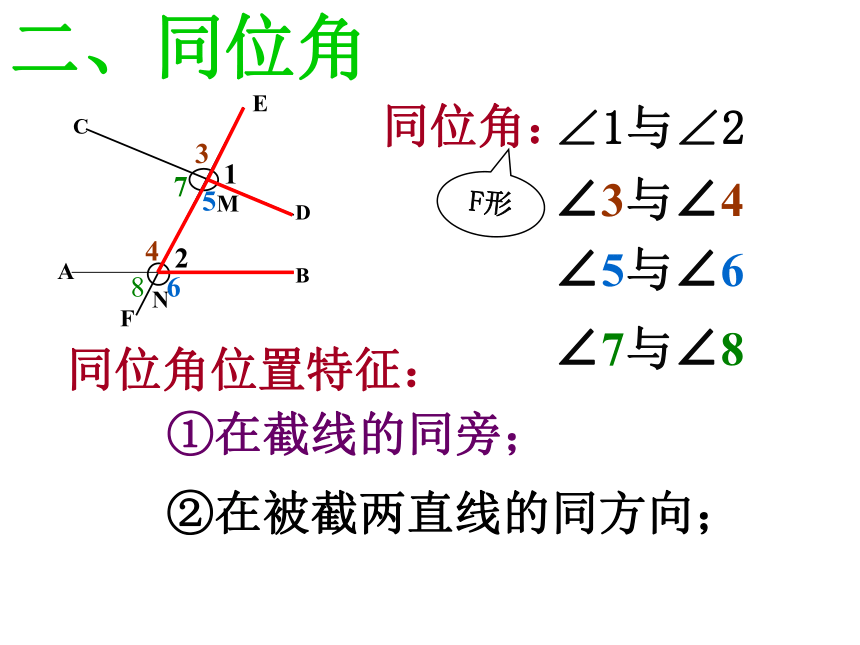
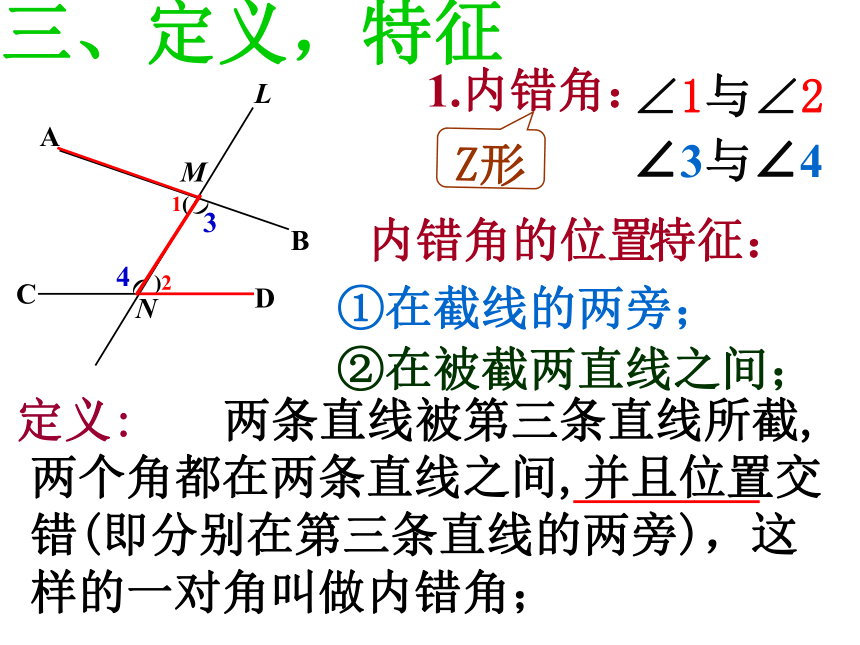
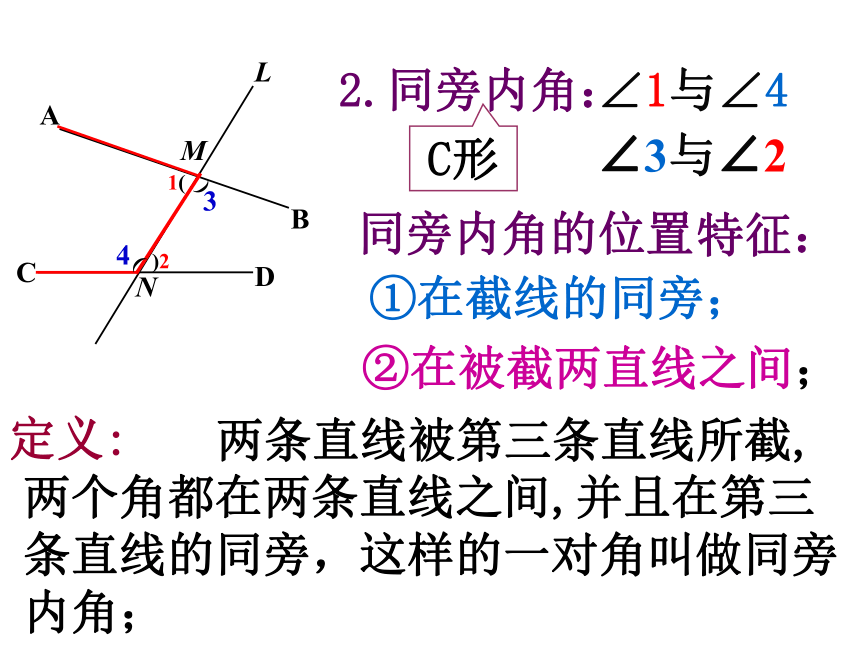
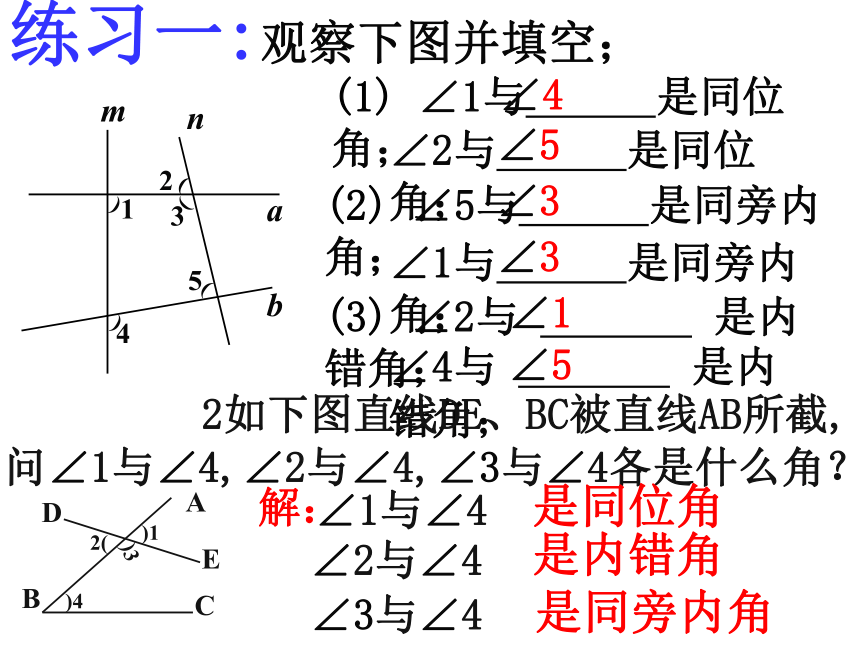
课件22张PPT。探索直线平行的条件一、复习1.判断直线平行的方法: 在同一平面内永不相交的两条直线互相平行;① 定义: ②如果两条直线都与第三条直线平行,那么这两条直线互相平行; 二、同位角∠1与∠2 ∠3与∠4 ∠5与∠6∠7与∠8 同位角:同位角位置特征:①在截线的同旁;②在被截两直线的同方向;F形ABCDEFMN特征:①在截线的两旁;②在被截两直线之间;1.内错角:∠3与∠4 Z形三、定义,特征内错角的位置MN定义: 两条直线被第三条直线所截,两个角都在两条直线之间,并且位置交错(即分别在第三条直线的两旁),这样的一对角叫做内错角;2.同旁内角:特征:①在截线的同旁;②在被截两直线之间;同旁内角的位置C形MN 两条直线被第三条直线所截,两个角都在两条直线之间,并且在第三条直线的同旁,这样的一对角叫做同旁内角;定义:练习一:观察下图并填空;(1) ∠1与 是同位角;∠4∠2与 是同位角;∠5(2) ∠5与 是同旁内角;∠3∠1与 是同旁内角;∠3(3) ∠2与 是内错角;∠1∠4与 是内错角;∠5 2如下图直线DE、BC被直线AB所截,问∠1与∠4,∠2与∠4,∠3与∠4各是什么角?是同位角是内错角是同旁内角在同一平面内,有两条直线a、b如何判断
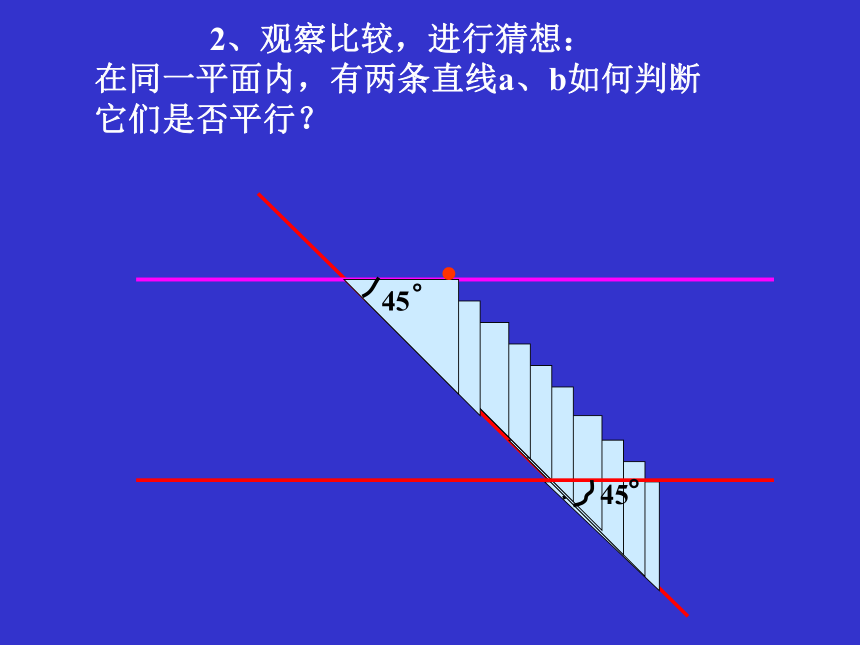
它们是否平行?.2、观察比较,进行猜想:.在同一平面内,有两条直线a、b如何判断
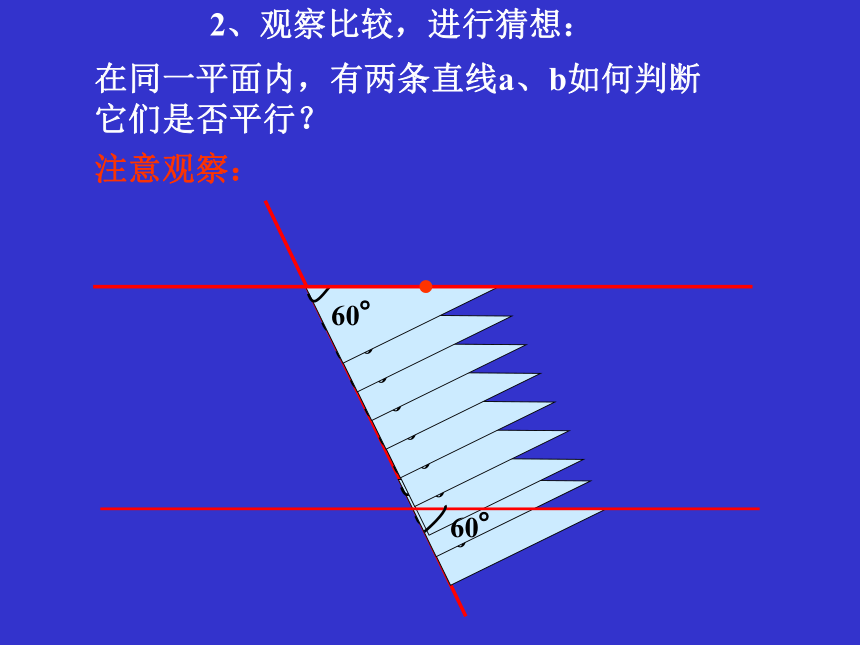
它们是否平行?注意观察:2、观察比较,进行猜想:在同一平面内,有两条直线a、b如何判断
它们是否平行?注意观察:2、观察比较,进行猜想:. 猜想:两条直线被第三条直线所截,如果同位
角相等,那么两直线平行。.2、观察比较,进行猜想: 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行。简单说成:同位角相等、两直线平行判定两条直线平行的公理:3、验证猜想:(揭示公理)1、你能说出木工师傅用图中这种角尺的工具画平行线的道理吗?cab124、及时巩固,及时反馈证明:∴∠1=∠2 (等量代换)∴a∥b (同位角相等、两直线平行)。练习1:
如图练习2:
如图5、讨论练习、巩固定理1、如图, BE是AB的延长线.
量得 ∠CBE=∠A从∠CBE=∠A ,可以判定哪两条直
线平行 ? 它的根据是什么?证明: ∵∠CBE=∠A (已知)∴AD∥BC (同位角相等、两直线平行)四、直线平行的条件简称:内错角相等,两直线平行;简称:同旁内角互补,两直线平行;1若:∠2=∠3能得到什么结论? 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;2若: ∠2+∠4=180о能得到什么结论?
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;探索:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?解:这两条直线平行。∵ a⊥b
∴∠1=90 °
∴ ∠1= ∠2∵c⊥a∴∠2=90°练一练1、∵∠1=∠4(已知)
∴ ∥ ( )2、∵∠ABC +∠ =180(已知)
∴AB∥CD( )3、∵∠ =∠ (已知)
∴AD∥BC( )4、∵∠5=∠ (已知)
∴AB∥CD( )5、如图,如果?1=?4,那么AB是否和CD平行,说明你的理由。∵∠1=∠2( )
∠1=∠4( )
∴ ∠4=∠2
∴AB∥CD( )6、如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。六、小结判断直线平行的方法: ① 定义:在同一平面内永不相交的两条直线互相平行;③同位角相等,两直线平行; ②如果两条直线都与第三条直线平行,那么这两条直线互相平行; ④内错角相等,两直线平行;⑤同旁内角互补,两直线平行;谢谢观赏!再见策划:李宏伟 王培琴
制作:苏朗
它们是否平行?.2、观察比较,进行猜想:.在同一平面内,有两条直线a、b如何判断
它们是否平行?注意观察:2、观察比较,进行猜想:在同一平面内,有两条直线a、b如何判断
它们是否平行?注意观察:2、观察比较,进行猜想:. 猜想:两条直线被第三条直线所截,如果同位
角相等,那么两直线平行。.2、观察比较,进行猜想: 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行。简单说成:同位角相等、两直线平行判定两条直线平行的公理:3、验证猜想:(揭示公理)1、你能说出木工师傅用图中这种角尺的工具画平行线的道理吗?cab124、及时巩固,及时反馈证明:∴∠1=∠2 (等量代换)∴a∥b (同位角相等、两直线平行)。练习1:
如图练习2:
如图5、讨论练习、巩固定理1、如图, BE是AB的延长线.
量得 ∠CBE=∠A从∠CBE=∠A ,可以判定哪两条直
线平行 ? 它的根据是什么?证明: ∵∠CBE=∠A (已知)∴AD∥BC (同位角相等、两直线平行)四、直线平行的条件简称:内错角相等,两直线平行;简称:同旁内角互补,两直线平行;1若:∠2=∠3能得到什么结论? 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;2若: ∠2+∠4=180о能得到什么结论?
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;探索:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?解:这两条直线平行。∵ a⊥b
∴∠1=90 °
∴ ∠1= ∠2∵c⊥a∴∠2=90°练一练1、∵∠1=∠4(已知)
∴ ∥ ( )2、∵∠ABC +∠ =180(已知)
∴AB∥CD( )3、∵∠ =∠ (已知)
∴AD∥BC( )4、∵∠5=∠ (已知)
∴AB∥CD( )5、如图,如果?1=?4,那么AB是否和CD平行,说明你的理由。∵∠1=∠2( )
∠1=∠4( )
∴ ∠4=∠2
∴AB∥CD( )6、如图,BC、DE分别平分?ABD和?BDF,且?1=?2,请找出平行线,并说明理由。六、小结判断直线平行的方法: ① 定义:在同一平面内永不相交的两条直线互相平行;③同位角相等,两直线平行; ②如果两条直线都与第三条直线平行,那么这两条直线互相平行; ④内错角相等,两直线平行;⑤同旁内角互补,两直线平行;谢谢观赏!再见策划:李宏伟 王培琴
制作:苏朗
