4.2.1指数函数的概念 课件(共30张PPT)
文档属性
| 名称 | 4.2.1指数函数的概念 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 23:22:05 | ||
图片预览





文档简介
(共30张PPT)
4.2.1 指数函数的概念
过程和方法
背景——概念——图象与性质——应用
一、情境导入
问题1
随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区门票。
二、背景研究
二、背景研究
问题1
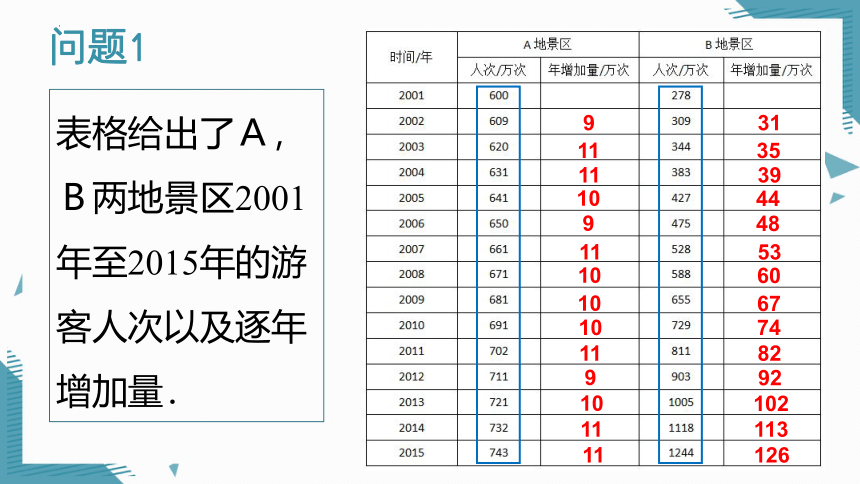
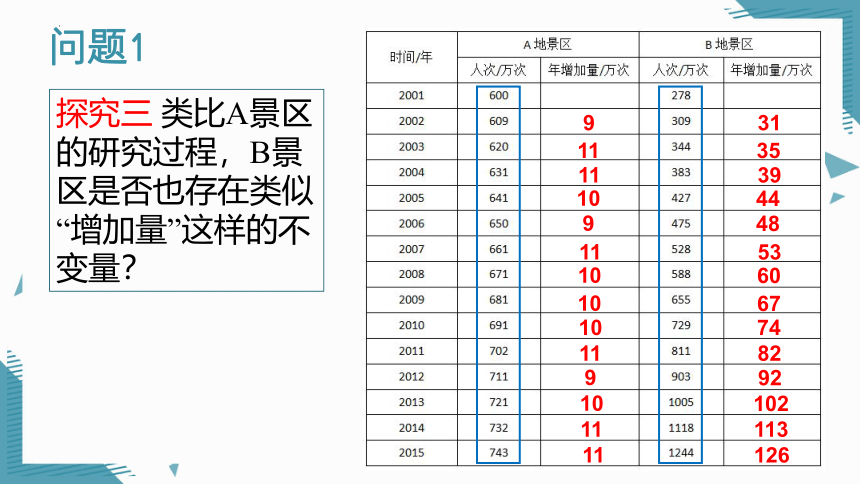
表格给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量.
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
探究一 根据表格信息,你们发现了怎样的变化规律?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
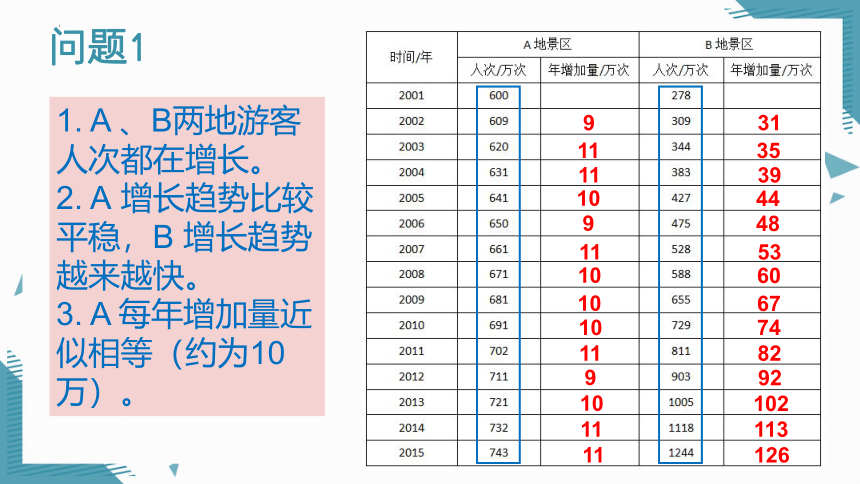
1. A 、B两地游客人次都在增长。
2. A 增长趋势比较平稳,B 增长趋势越来越快。
3. A 每年增加量近似相等(约为10万)。
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
探究一 比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
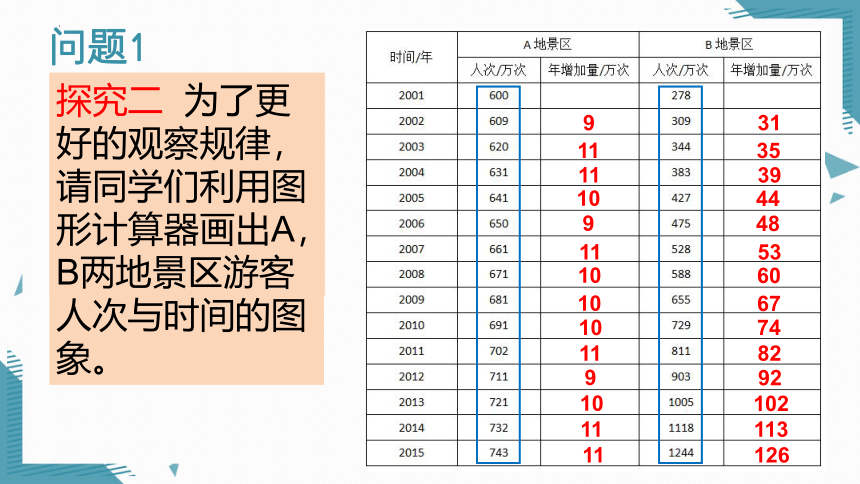
探究二 为了更好的观察规律,请同学们利用图形计算器画出A,B两地景区游客人次与时间的图象。
问题1
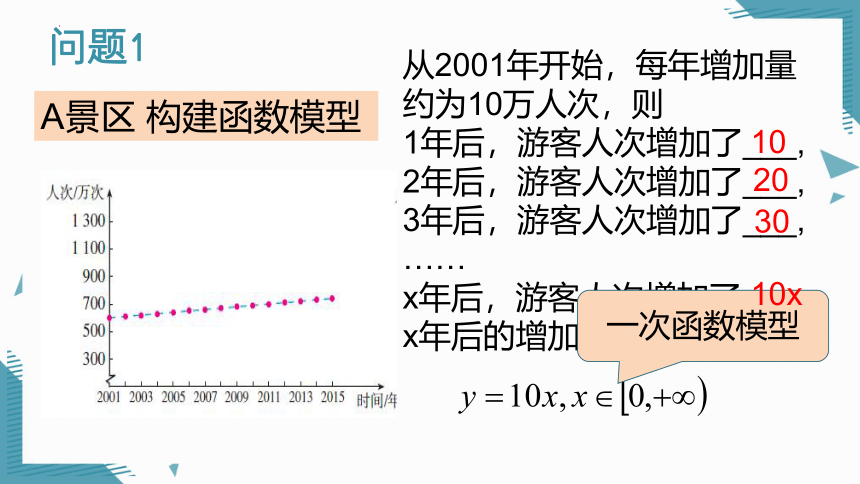
从2001年开始,每年增加量约为10万人次,则
1年后,游客人次增加了___,
2年后,游客人次增加了___,
3年后,游客人次增加了___,
……
x年后,游客人次增加了___,
x年后的增加量记为y,则
一次函数模型
10
20
30
10x
A景区 构建函数模型
问题1
探究三 类比A景区的研究过程,B景区是否也存在类似“增加量”这样的不变量?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
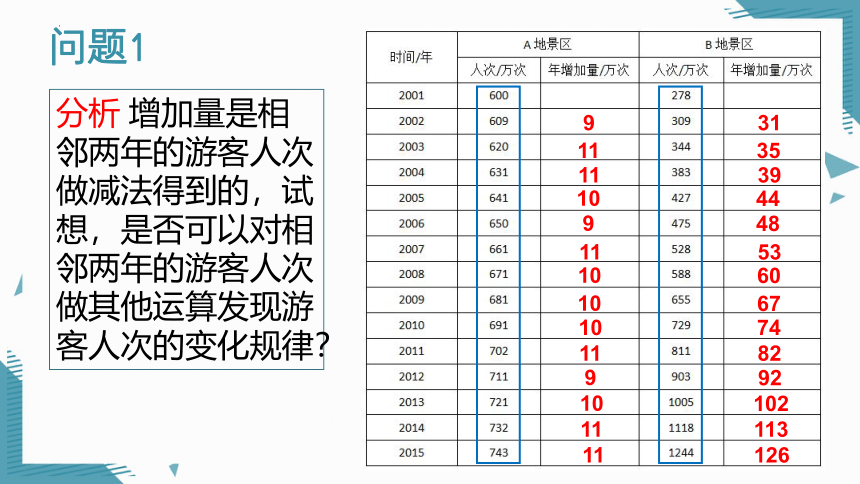
问题1
分析 增加量是相邻两年的游客人次做减法得到的,试想,是否可以对相邻两年的游客人次做其他运算发现游客人次的变化规律?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
根据增长率的计算公式,可以知道B景区游客人次
每年的增长率约为1.11-1=0.11。
像这样,增长率为常数的变化方式,我们称为指数增长。
是一个常数
问题1
探究四 B地景区游客人次呈指数增长,如何
构建新的函数模型。
从2001年开始,B地景区游客人次的变化规律可以描述为:
1年后,游客人次是2001年的___________倍;
2年后,游客人次是2001年的___________倍;
3年后,游客人次是2001年的___________倍;
……
x年后,游客人次是2001年的___________倍;
问题1
设经过 x 年后的游客人次为2001年的 y 倍,则
探究四 B地景区游客人次呈指数增长,如何
构建新的函数模型。
小结 增加量、增长率是刻画事物变化规律的两个很重要的量。
问题2
当生物死亡后,它机体内原有的碳14含
量会按确定的比率衰减(称为衰减率),大
约每经过5730年衰减为原来的一半,这个时
间称为“半衰期”.按照上述变化规律,生
物体内碳14含量与死亡年数之间有怎样的关
系?
二、背景研究
二、背景研究
问题2
不妨设刚死亡的生物体内碳14的含量看成1个单位,死亡生物体内碳14含量的年衰减率为
死亡1年后,生物体内碳14含量为__________;
死亡2年后,生物体内碳14含量为__________;
死亡3年后,生物体内碳14含量为__________;
……
死亡x年后,生物体内碳14含量为__________;
设死亡x年后,生物体内碳14含量为y,则
问题2
根据已知条件,当 时,
像这样,衰减率为常数的变化方式,我们称为指数衰减。
指数函数概念
追问1:像 这类函数与我们
刚刚学过的幂函数 一样吗?
这两类函数有什么区别?
追问2:从这两个解析式中能否抽象出一个更具有一般性的函数模型?
用字母 代替常数 ,则有
二、背景研究
二、背景研究
不一样。
自变量x的位置不同。
指数函数概念
一般地,函数 叫做
指数函数,其中指数 是自变量,定义域是R.
追问1: 为什么规定 的范围为 。
为了便于研究,规定:
三、新知归纳
指数函数概念
一般地,函数 叫做
指数函数,其中指数 是自变量,定义域是R.
追问2:指数函数是单项式还是多项式。
追问3:指数函数的系数是_____。
追问4:自变量x在_____(指数、底数)位置,是它本身。
单项式
指数
三、新知归纳
指数函数概念
一般地,函数 叫做
指数函数,其中指数 是自变量,定义域是R.
特点:
1. 函数式是幂的形式;
2. 是单项式,系数为1;
3. 指数为自变量x;
4. 底数 的范围:
三、新知归纳
概念辨析
2. 函数 是指数函数,则有( )
1. 判断下列函数是否是指数函数?
(3)(5)(6)
四、概念辨析
概念应用
例1 已知指数函数 ,且
,求 的值。
分析:要求f(0),f(1),f(-3)的值,应先求出f(x)=ax 的解析式,即先求a的值.
四、概念辨析
概念应用
例1 已知指数函数 ,且
,求 的值。
解:因为f(x)=ax,且f(3)=π,则a3=π ,解得 ,
于是
所以,
总结:待定系数法确定指数函数解析式,只需列一个方程.
四、概念辨析
课堂练习
1. 下列图象中,有可能表示指数函数的是( ).
2.若函数 是指数函数,则 的范围是( )
五、课堂练习
课堂练习
3. 函数 是指数函数,求
解:
五、课堂练习
生活中的指数函数模型
细胞的分裂
细胞分裂时,由
1次分裂成2个,
2次分裂成4个,
3次分裂成8个,
……
如果细胞分裂x次,相应的细胞个数为y,
生活中的指数函数模型
生活中的指数函数模型
《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
把尺子的长度看做单位1.
第1天,取一半 ,
第2天,取一半 ,
第3天,取一半 ,
……
第x天,取一半 ,
此时剩余长度,记为y
生活中的指数函数模型
课堂小结
学习指数函数的概念。
数形结合,类比,待定系数法,由具体到抽象等思想方法,提升直观想象、逻辑推理、数学运算、数学抽象核心素养。
利用图形计算器对数据处理,提升数据分析,直观想象核心素养。通过构建函数模型,提升数学建模核心素养。
六、归纳总结
基本知识与技能:
基本思想方法:
基本活动经验:
课后作业
课本第115页,练习:第2,3题。
课后延伸:
课本第115页,阅读与思考:放射性物质
的衰减。
七、课后作业
感谢您的聆听!
4.2.1 指数函数的概念
过程和方法
背景——概念——图象与性质——应用
一、情境导入
问题1
随着中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式.由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区门票。
二、背景研究
二、背景研究
问题1
表格给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量.
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
探究一 根据表格信息,你们发现了怎样的变化规律?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
1. A 、B两地游客人次都在增长。
2. A 增长趋势比较平稳,B 增长趋势越来越快。
3. A 每年增加量近似相等(约为10万)。
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
探究一 比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
探究二 为了更好的观察规律,请同学们利用图形计算器画出A,B两地景区游客人次与时间的图象。
问题1
从2001年开始,每年增加量约为10万人次,则
1年后,游客人次增加了___,
2年后,游客人次增加了___,
3年后,游客人次增加了___,
……
x年后,游客人次增加了___,
x年后的增加量记为y,则
一次函数模型
10
20
30
10x
A景区 构建函数模型
问题1
探究三 类比A景区的研究过程,B景区是否也存在类似“增加量”这样的不变量?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
分析 增加量是相邻两年的游客人次做减法得到的,试想,是否可以对相邻两年的游客人次做其他运算发现游客人次的变化规律?
9
11
11
10
9
11
10
10
10
11
9
10
11
11
31
35
39
44
48
53
60
67
74
82
92
102
113
126
问题1
根据增长率的计算公式,可以知道B景区游客人次
每年的增长率约为1.11-1=0.11。
像这样,增长率为常数的变化方式,我们称为指数增长。
是一个常数
问题1
探究四 B地景区游客人次呈指数增长,如何
构建新的函数模型。
从2001年开始,B地景区游客人次的变化规律可以描述为:
1年后,游客人次是2001年的___________倍;
2年后,游客人次是2001年的___________倍;
3年后,游客人次是2001年的___________倍;
……
x年后,游客人次是2001年的___________倍;
问题1
设经过 x 年后的游客人次为2001年的 y 倍,则
探究四 B地景区游客人次呈指数增长,如何
构建新的函数模型。
小结 增加量、增长率是刻画事物变化规律的两个很重要的量。
问题2
当生物死亡后,它机体内原有的碳14含
量会按确定的比率衰减(称为衰减率),大
约每经过5730年衰减为原来的一半,这个时
间称为“半衰期”.按照上述变化规律,生
物体内碳14含量与死亡年数之间有怎样的关
系?
二、背景研究
二、背景研究
问题2
不妨设刚死亡的生物体内碳14的含量看成1个单位,死亡生物体内碳14含量的年衰减率为
死亡1年后,生物体内碳14含量为__________;
死亡2年后,生物体内碳14含量为__________;
死亡3年后,生物体内碳14含量为__________;
……
死亡x年后,生物体内碳14含量为__________;
设死亡x年后,生物体内碳14含量为y,则
问题2
根据已知条件,当 时,
像这样,衰减率为常数的变化方式,我们称为指数衰减。
指数函数概念
追问1:像 这类函数与我们
刚刚学过的幂函数 一样吗?
这两类函数有什么区别?
追问2:从这两个解析式中能否抽象出一个更具有一般性的函数模型?
用字母 代替常数 ,则有
二、背景研究
二、背景研究
不一样。
自变量x的位置不同。
指数函数概念
一般地,函数 叫做
指数函数,其中指数 是自变量,定义域是R.
追问1: 为什么规定 的范围为 。
为了便于研究,规定:
三、新知归纳
指数函数概念
一般地,函数 叫做
指数函数,其中指数 是自变量,定义域是R.
追问2:指数函数是单项式还是多项式。
追问3:指数函数的系数是_____。
追问4:自变量x在_____(指数、底数)位置,是它本身。
单项式
指数
三、新知归纳
指数函数概念
一般地,函数 叫做
指数函数,其中指数 是自变量,定义域是R.
特点:
1. 函数式是幂的形式;
2. 是单项式,系数为1;
3. 指数为自变量x;
4. 底数 的范围:
三、新知归纳
概念辨析
2. 函数 是指数函数,则有( )
1. 判断下列函数是否是指数函数?
(3)(5)(6)
四、概念辨析
概念应用
例1 已知指数函数 ,且
,求 的值。
分析:要求f(0),f(1),f(-3)的值,应先求出f(x)=ax 的解析式,即先求a的值.
四、概念辨析
概念应用
例1 已知指数函数 ,且
,求 的值。
解:因为f(x)=ax,且f(3)=π,则a3=π ,解得 ,
于是
所以,
总结:待定系数法确定指数函数解析式,只需列一个方程.
四、概念辨析
课堂练习
1. 下列图象中,有可能表示指数函数的是( ).
2.若函数 是指数函数,则 的范围是( )
五、课堂练习
课堂练习
3. 函数 是指数函数,求
解:
五、课堂练习
生活中的指数函数模型
细胞的分裂
细胞分裂时,由
1次分裂成2个,
2次分裂成4个,
3次分裂成8个,
……
如果细胞分裂x次,相应的细胞个数为y,
生活中的指数函数模型
生活中的指数函数模型
《庄子·天下篇》中写道:
“一尺之棰,日取之半,万世不竭”
把尺子的长度看做单位1.
第1天,取一半 ,
第2天,取一半 ,
第3天,取一半 ,
……
第x天,取一半 ,
此时剩余长度,记为y
生活中的指数函数模型
课堂小结
学习指数函数的概念。
数形结合,类比,待定系数法,由具体到抽象等思想方法,提升直观想象、逻辑推理、数学运算、数学抽象核心素养。
利用图形计算器对数据处理,提升数据分析,直观想象核心素养。通过构建函数模型,提升数学建模核心素养。
六、归纳总结
基本知识与技能:
基本思想方法:
基本活动经验:
课后作业
课本第115页,练习:第2,3题。
课后延伸:
课本第115页,阅读与思考:放射性物质
的衰减。
七、课后作业
感谢您的聆听!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
