2023秋人教版六年级数学上册 等积变形(课件)(共34张PPT)
文档属性
| 名称 | 2023秋人教版六年级数学上册 等积变形(课件)(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 18:35:16 | ||
图片预览


文档简介
(共34张PPT)
2023秋 人教数学
六年级上册
等积变形
巧用三角形同底等高、同高等底求面积
10cm
10cm
知识回顾:1. 三角形面积
S▲ABC= BC×AH
B
C
A
H
S▲= 底×高
10cm
B
C
A
D
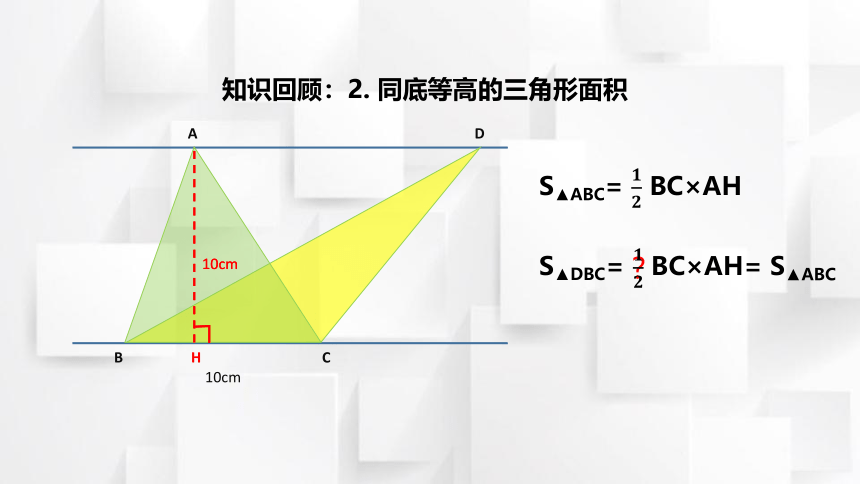
知识回顾:2. 同底等高的三角形面积
S▲ABC= BC×AH
10cm
H
S▲DBC=
10cm
?
BC×AH= S▲ABC
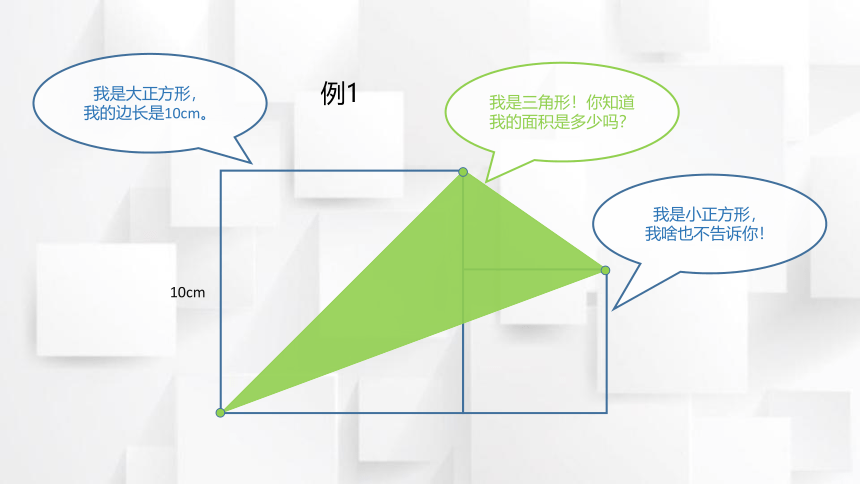
我是大正方形,
我的边长是10cm。
10cm
我是小正方形,
我啥也不告诉你!
我是三角形!你知道我的面积是多少吗?
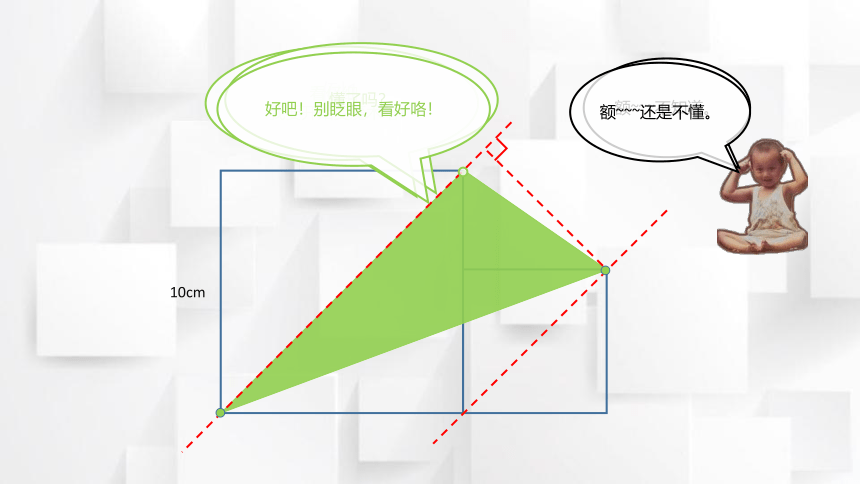
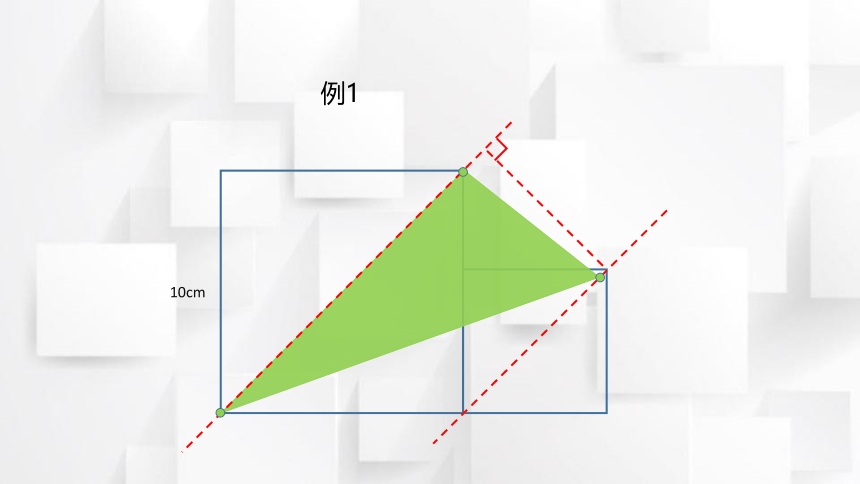
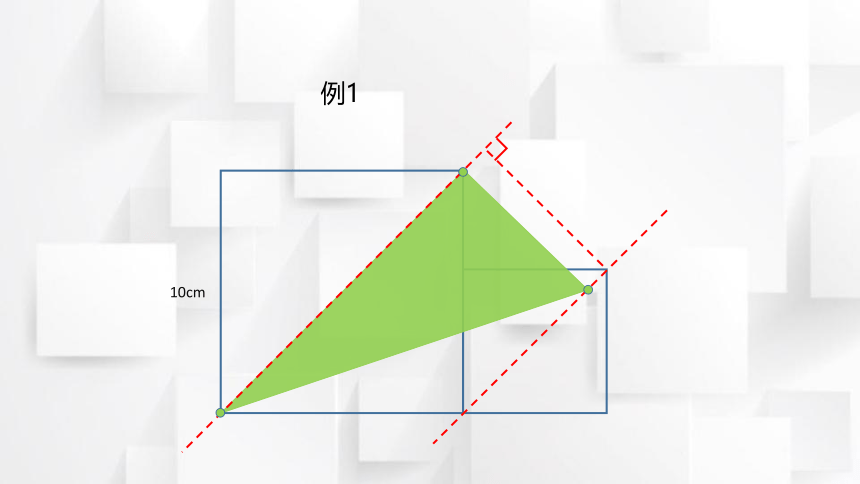
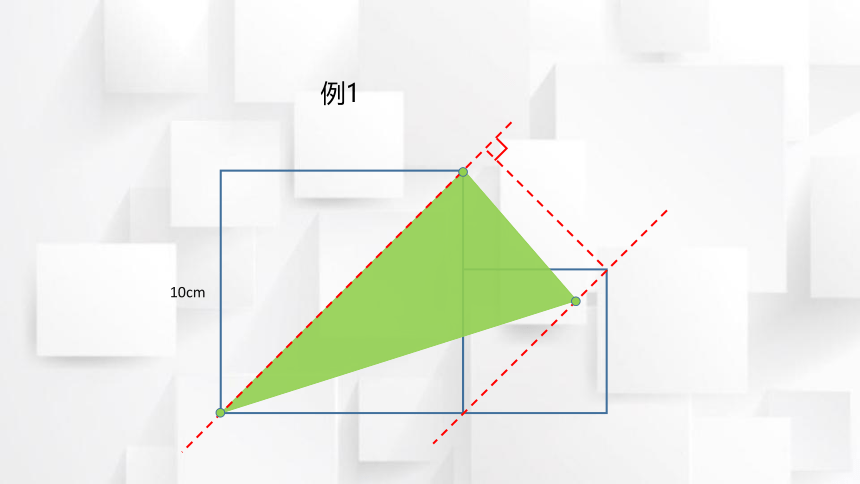
例1
例1
10cm
看仔细,
我要开始变魔术咯!
额~~~不知道。
懂了吗?
额~~~还是不懂。
好吧!别眨眼,看好咯!
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
例1
10cm
懂啦,懂啦!
懂了吗!
这不就10×10÷2=50(c㎡)嘛!
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
小朋友们,你们懂了吗!
一起来看看吧!
同学们,
一起来试一试吧!
6cm
你知道我的面积是多少吗?
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
重点知识回顾
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
你算出来了吗?
变式1
6×6÷2=18(cm2)
6cm
我还有个兄弟,你知道它的面积是多少吗?
变式1
6cm
猜猜我的面积吧?
这下知道了吧!
变式2
还是6×6÷2=18(cm2)
你知道为什么吗?
是高手就来挑战
我的面积吧!
10cm
8cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
重点知识回顾
3
例2
我与例1有什么区别呢?
与3个正方形有关的三角形
A
C
E
B
D
F
S▲ECD= S▲ACD - S▲ACE
S▲ACD= AC×CD
S▲ACE= AC×BE
是高手就来挑战
我的面积吧!
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
重点知识回顾
3
变式
没有边在对角线上,
怎么办?
有对角线在三角形里面吗?
按提示自己算一算吧!
找2或3个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
重点知识回顾
一个直角梯形的对角线分出4个三角形,已知其中两个为8cm2和4cm2,如图。
求直角梯形ABCD面积。
A
B
C
D
O
8cm2
4cm2
4cm2
例3:
一个直角梯形的对角线分出4个三角形,已知其中两个为8cm2和4cm2,如图。
求直角梯形ABCD面积。
A
B
C
D
O
8cm2
4cm2
4cm2
∴ OB:OD = 2:1
又∵▲ABO与▲ADO同高AF
∴ S▲ABO:S▲ADO= OB×AF: OD× AF =2:1
2cm2
∴ S梯ABCD=2+4+4+8=18 cm2
例3:
F
E
∵ S▲COB:S▲ COD = OB×CE: OD×CE=8:4=2:1
作CE⊥BD于点E
∴ S▲ADO =4×
作AF⊥BD于点F
已知▲ABO面积为9cm2,线段BO长是DO的3倍
求梯形ABCD的面积。
A
B
C
D
O
9cm2
变式:
你有什么收获?
用同底等高的三角形面积相等来解决问题
用等高且底成比例的三角形面积也成比例来解决问题
面积转化思想
谢谢观看
2023秋 人教数学
六年级上册
等积变形
巧用三角形同底等高、同高等底求面积
10cm
10cm
知识回顾:1. 三角形面积
S▲ABC= BC×AH
B
C
A
H
S▲= 底×高
10cm
B
C
A
D
知识回顾:2. 同底等高的三角形面积
S▲ABC= BC×AH
10cm
H
S▲DBC=
10cm
?
BC×AH= S▲ABC
我是大正方形,
我的边长是10cm。
10cm
我是小正方形,
我啥也不告诉你!
我是三角形!你知道我的面积是多少吗?
例1
例1
10cm
看仔细,
我要开始变魔术咯!
额~~~不知道。
懂了吗?
额~~~还是不懂。
好吧!别眨眼,看好咯!
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
10cm
例1
例1
10cm
懂啦,懂啦!
懂了吗!
这不就10×10÷2=50(c㎡)嘛!
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
小朋友们,你们懂了吗!
一起来看看吧!
同学们,
一起来试一试吧!
6cm
你知道我的面积是多少吗?
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
重点知识回顾
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
变式1
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
你算出来了吗?
变式1
6×6÷2=18(cm2)
6cm
我还有个兄弟,你知道它的面积是多少吗?
变式1
6cm
猜猜我的面积吧?
这下知道了吧!
变式2
还是6×6÷2=18(cm2)
你知道为什么吗?
是高手就来挑战
我的面积吧!
10cm
8cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
重点知识回顾
3
例2
我与例1有什么区别呢?
与3个正方形有关的三角形
A
C
E
B
D
F
S▲ECD= S▲ACD - S▲ACE
S▲ACD= AC×CD
S▲ACE= AC×BE
是高手就来挑战
我的面积吧!
6cm
找两个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
重点知识回顾
3
变式
没有边在对角线上,
怎么办?
有对角线在三角形里面吗?
按提示自己算一算吧!
找2或3个正方形平行的对角线,且有一条是三角形的底边。
2. 平行线上移动三角
形顶点,至已知边
长正方形顶点重合。
重点知识回顾
一个直角梯形的对角线分出4个三角形,已知其中两个为8cm2和4cm2,如图。
求直角梯形ABCD面积。
A
B
C
D
O
8cm2
4cm2
4cm2
例3:
一个直角梯形的对角线分出4个三角形,已知其中两个为8cm2和4cm2,如图。
求直角梯形ABCD面积。
A
B
C
D
O
8cm2
4cm2
4cm2
∴ OB:OD = 2:1
又∵▲ABO与▲ADO同高AF
∴ S▲ABO:S▲ADO= OB×AF: OD× AF =2:1
2cm2
∴ S梯ABCD=2+4+4+8=18 cm2
例3:
F
E
∵ S▲COB:S▲ COD = OB×CE: OD×CE=8:4=2:1
作CE⊥BD于点E
∴ S▲ADO =4×
作AF⊥BD于点F
已知▲ABO面积为9cm2,线段BO长是DO的3倍
求梯形ABCD的面积。
A
B
C
D
O
9cm2
变式:
你有什么收获?
用同底等高的三角形面积相等来解决问题
用等高且底成比例的三角形面积也成比例来解决问题
面积转化思想
谢谢观看
