2023秋人教版六年级数学上册 巧求阴影部分面积(课件)(共27张PPT)
文档属性
| 名称 | 2023秋人教版六年级数学上册 巧求阴影部分面积(课件)(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 18:39:36 | ||
图片预览


文档简介
(共27张PPT)
2023秋 人教数学
六年级上册
巧求阴影部分面积
转化思维的应用
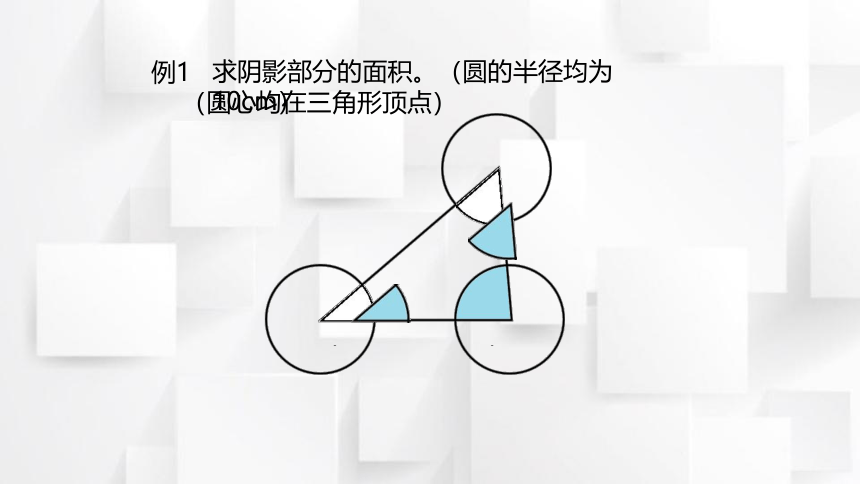
求阴影部分的面积。(圆的半径均为10cm)
例1
(圆心均在三角形顶点)
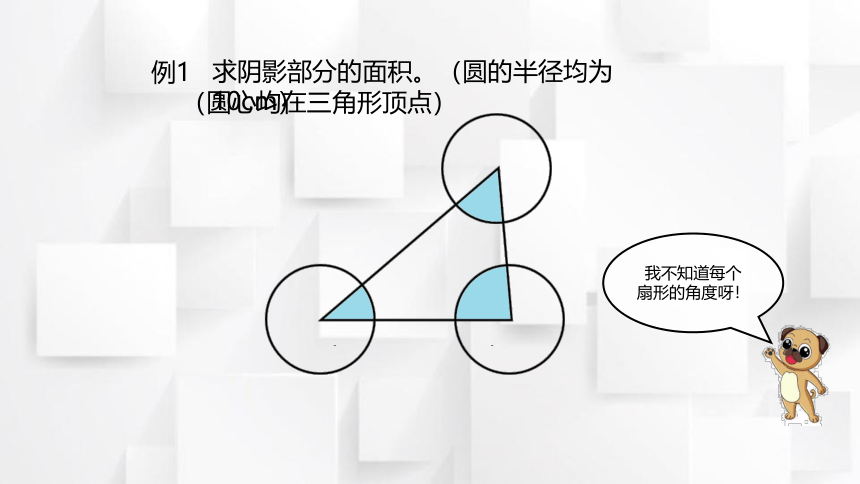
求阴影部分的面积。(圆的半径均为10cm)
我不知道每个
扇形的角度呀!
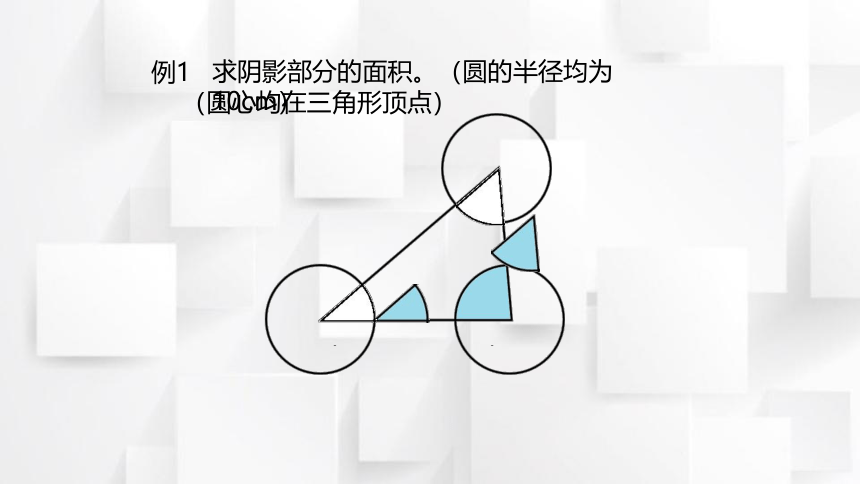
例1
(圆心均在三角形顶点)
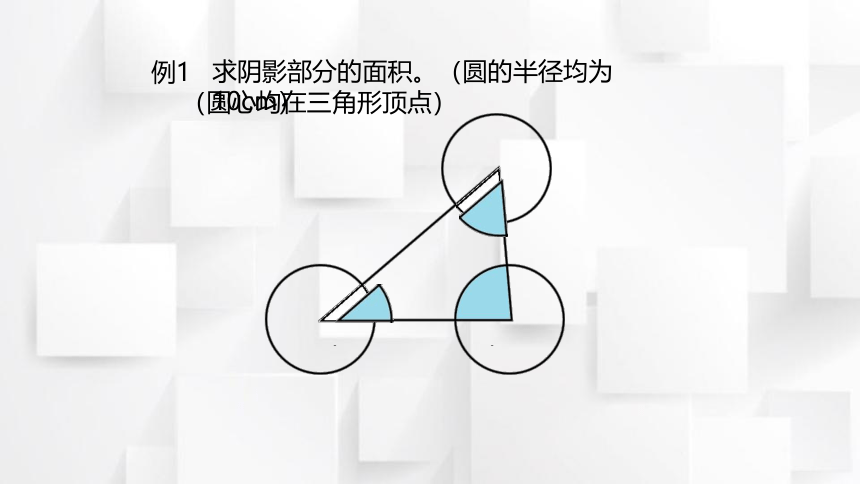
求阴影部分的面积。(圆的半径均为10cm)
例1
(圆心均在三角形顶点)
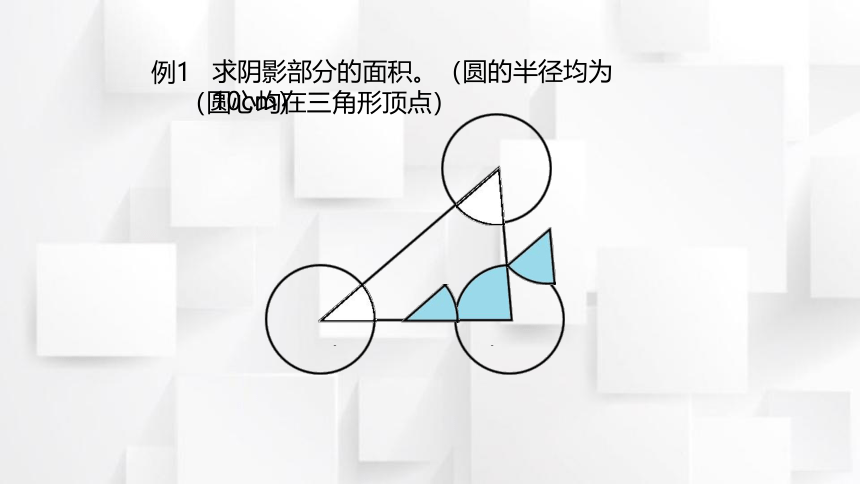
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
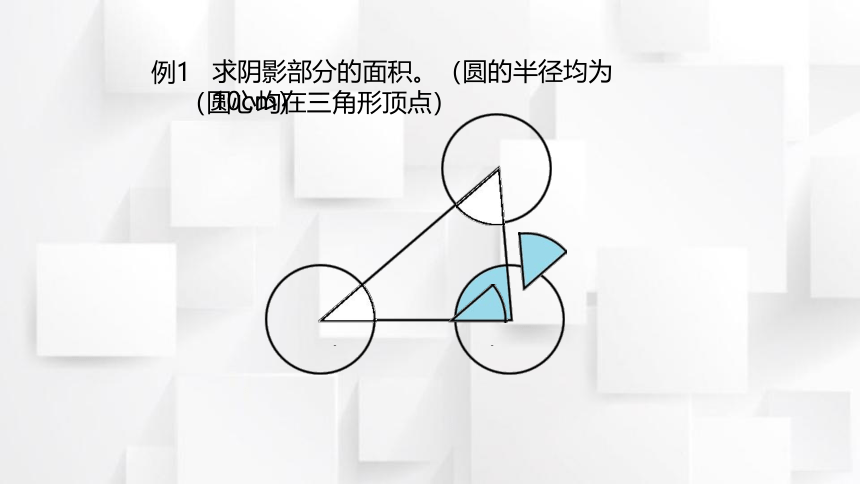
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
S阴= S半圆
这下我知道啦!
那它为什么刚好是个半圆呢?
中间图形的内角和
例1
三角形内角和180°
求阴影部分的面积。(圆的半径均为10cm)
180°是平角,但边怎么能刚好合成半圆呢?
(圆心均在三角形顶点)
我明白了!
=102π× = 314 × = 157(平方厘米)
求阴影部分的面积。(圆的半径均为10cm)
找到中间图形的内角和了吗?
变式1
平行四边形内角和360°
∴ S阴= S圆
(圆心均在三角形顶点)
找到中间图形的内角和了吗?
变式2
求阴影部分的面积。(圆的半径均为10cm)
直角梯形内角和360°
∴ S阴= S圆
对吗???
比直角梯形少了个直角90°!
∴ S阴= S圆×
也就是360°少了,剩了
(圆心均在三角形顶点)
变式3
求阴影部分的面积。(圆的半径均为10cm)
S阴是一个圆面积的多少呢?
∴ S阴= S圆×
(圆心均在三角形顶点)
找到中间图形的内角和了吗?
变式4
求阴影部分的面积。(圆的半径均为10cm)
正n边形的内角和度数为:
(n-2)×180°
正五边形的内角和度数为:
(5-2)×180°=540°
360°:540°=2:3
∴ S阴= S圆×
(圆心均在三角形顶点)
求阴影部分的面积。(正方形对角线长为20cm)
S阴= S▲
例2
阴影部分为好几部分
能不能组合一下呢?
通过移动、拼接
凑成方便计算的图形
=(20÷2) ×
= 50(平方厘米)
求阴影部分的面积。(长方形短边长为5cm)
变式1
阴影部分能不能分开
再重新组合成方便计算的呢?
通过拆分、移动、拼接
凑成方便计算的图形
S阴=S正- S圆
求阴影部分的面积。(圆的半径为10cm)
例3
求阴影部分的面积。(圆的半径为10cm)
例3
4个直角扇形好像能合成一个圆!
单独把扇形剪出来拼吗?
阴影部分没有变化呀!
通过拆分、移动、拼接
凑成方便计算的图形
横平竖直拆分
试试呢!
求阴影部分的面积。(圆的半径为10cm)
例3
通过拆分、移动、拼接
凑成方便计算的图形
求阴影部分的面积。(圆的半径为10cm)
例3
通过拆分、移动、拼接
凑成方便计算的图形
求阴影部分的面积。(圆的半径为10cm)
例3
这下我知道啦!
S阴= S正-S圆
=(10+10)2 - 102π= 400 - 314 = 86(cm2)
通过拆分、移动、拼接
凑成方便计算的图形
5
求阴影部分的面积。(单位:厘米)
变式1
5
S阴= S圆-S▲
S阴= (S圆-S▲)×2
求阴影部分的面积。(单位:厘米)
10
变式2
S阴= (S圆-S▲)×2
×4
注意半径与三角形直角边长
求阴影部分的面积。(单位:厘米)
10
变式3
两图阴影部分面积???
今天,你学会了什么?
通过拆分、移动、拼接
凑成方便计算的图形
转化思想
谢谢观看
2023秋 人教数学
六年级上册
巧求阴影部分面积
转化思维的应用
求阴影部分的面积。(圆的半径均为10cm)
例1
(圆心均在三角形顶点)
求阴影部分的面积。(圆的半径均为10cm)
我不知道每个
扇形的角度呀!
例1
(圆心均在三角形顶点)
求阴影部分的面积。(圆的半径均为10cm)
例1
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
例1
求阴影部分的面积。(圆的半径均为10cm)
(圆心均在三角形顶点)
S阴= S半圆
这下我知道啦!
那它为什么刚好是个半圆呢?
中间图形的内角和
例1
三角形内角和180°
求阴影部分的面积。(圆的半径均为10cm)
180°是平角,但边怎么能刚好合成半圆呢?
(圆心均在三角形顶点)
我明白了!
=102π× = 314 × = 157(平方厘米)
求阴影部分的面积。(圆的半径均为10cm)
找到中间图形的内角和了吗?
变式1
平行四边形内角和360°
∴ S阴= S圆
(圆心均在三角形顶点)
找到中间图形的内角和了吗?
变式2
求阴影部分的面积。(圆的半径均为10cm)
直角梯形内角和360°
∴ S阴= S圆
对吗???
比直角梯形少了个直角90°!
∴ S阴= S圆×
也就是360°少了,剩了
(圆心均在三角形顶点)
变式3
求阴影部分的面积。(圆的半径均为10cm)
S阴是一个圆面积的多少呢?
∴ S阴= S圆×
(圆心均在三角形顶点)
找到中间图形的内角和了吗?
变式4
求阴影部分的面积。(圆的半径均为10cm)
正n边形的内角和度数为:
(n-2)×180°
正五边形的内角和度数为:
(5-2)×180°=540°
360°:540°=2:3
∴ S阴= S圆×
(圆心均在三角形顶点)
求阴影部分的面积。(正方形对角线长为20cm)
S阴= S▲
例2
阴影部分为好几部分
能不能组合一下呢?
通过移动、拼接
凑成方便计算的图形
=(20÷2) ×
= 50(平方厘米)
求阴影部分的面积。(长方形短边长为5cm)
变式1
阴影部分能不能分开
再重新组合成方便计算的呢?
通过拆分、移动、拼接
凑成方便计算的图形
S阴=S正- S圆
求阴影部分的面积。(圆的半径为10cm)
例3
求阴影部分的面积。(圆的半径为10cm)
例3
4个直角扇形好像能合成一个圆!
单独把扇形剪出来拼吗?
阴影部分没有变化呀!
通过拆分、移动、拼接
凑成方便计算的图形
横平竖直拆分
试试呢!
求阴影部分的面积。(圆的半径为10cm)
例3
通过拆分、移动、拼接
凑成方便计算的图形
求阴影部分的面积。(圆的半径为10cm)
例3
通过拆分、移动、拼接
凑成方便计算的图形
求阴影部分的面积。(圆的半径为10cm)
例3
这下我知道啦!
S阴= S正-S圆
=(10+10)2 - 102π= 400 - 314 = 86(cm2)
通过拆分、移动、拼接
凑成方便计算的图形
5
求阴影部分的面积。(单位:厘米)
变式1
5
S阴= S圆-S▲
S阴= (S圆-S▲)×2
求阴影部分的面积。(单位:厘米)
10
变式2
S阴= (S圆-S▲)×2
×4
注意半径与三角形直角边长
求阴影部分的面积。(单位:厘米)
10
变式3
两图阴影部分面积???
今天,你学会了什么?
通过拆分、移动、拼接
凑成方便计算的图形
转化思想
谢谢观看
