11.3.1多边形 同步练习 2023-2024学年八年级数学上学期人教版(含答案)
文档属性
| 名称 | 11.3.1多边形 同步练习 2023-2024学年八年级数学上学期人教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览


文档简介
11.3.1多边形 同步练习
一、单选题
1.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )
A.0根 B.1根 C.2根 D.5根
2.一个多边形从一个顶点最多能引出四条对角线,这个多边形是( )
A.四角形 B.五边形 C.六边形 D.七边形
3.若边形恰好有条对角线,则为( )
A.4 B.5 C.6 D.7
4.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成6个三角形,那么这个多边形是( )
A.6边形 B.7边形 C.8边形 D.9边形
5.一个四边形截去一个角后内角个数是( )
A.3 B.4 C.5 D.3、4、5
6.下列命题正确的是( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等、各角也相等的多边形是正多边形
7.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2011个三角形,那么这个多边形是 ( )
A.2012边形 B.2013边形 C.2014边形 D.2015边形
8.如图,在边长为的小正方形网格中,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形图中①,②,③,④四个格点多边形的面积分别记为下列说法正确的是( )
A. B. C. D.
二、填空题
9.一个正八边形,从它的一个顶点可引出m条对角线,并把这个正八边形分成n个三角形,则 .
10.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则 .
11.如图所示的网格是正方形网格,点A,B,C,D是网格线交点,则的面积与的面积大小关系为: (填“>”“=”或“<”),
12.把一张长方形纸片剪去一个角后,还剩 个角.
13.如图,伸缩晾衣架利用的几何原理是四边形的 .
三、解答题
14.画图题:
(1)如图①从多边形的一个顶点出发画对角线,把多边形分割成三角形;
(2)如图②从多边形的一条边上的一点出发画对角线,把多边形分割成三角形;
(3)如图③从多边形的内部一点出发画对角线,把多边形分割成三角形.
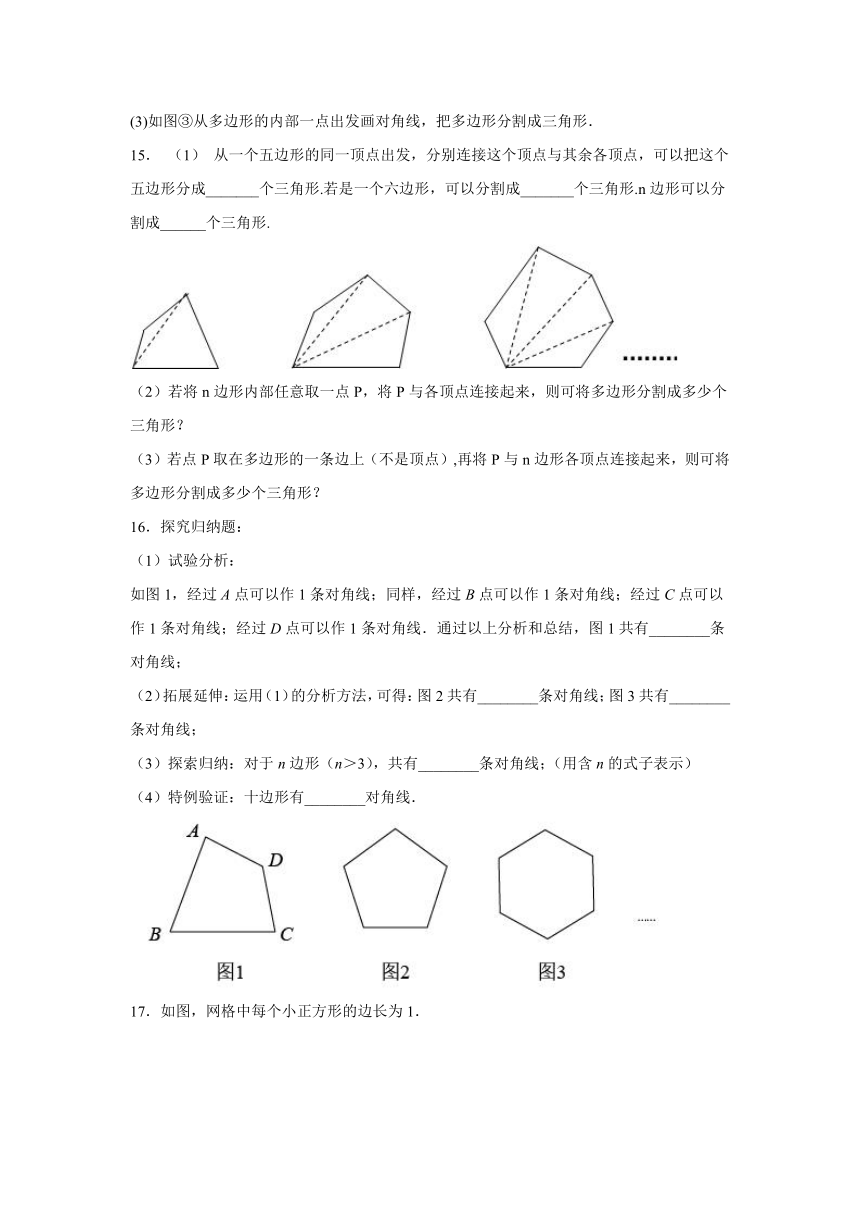
15. (1) 从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成_______个三角形.若是一个六边形,可以分割成_______个三角形.n边形可以分割成______个三角形.
(2)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?
(3)若点P取在多边形的一条边上(不是顶点),再将P与n边形各顶点连接起来,则可将多边形分割成多少个三角形?
16.探究归纳题:
(1)试验分析:
如图1,经过A点可以作1条对角线;同样,经过B点可以作1条对角线;经过C点可以作1条对角线;经过D点可以作1条对角线.通过以上分析和总结,图1共有________条对角线;
(2)拓展延伸:运用(1)的分析方法,可得:图2共有________条对角线;图3共有________条对角线;
(3)探索归纳:对于n边形(n>3),共有________条对角线;(用含n的式子表示)
(4)特例验证:十边形有________对角线.
17.如图,网格中每个小正方形的边长为1.
(1)求阴影部分的面积;
(2)把图中阴影部分通过剪拼形成一个正方形,设正方形的边长为a.已知a的整数部分和小数部分分别是x和y,求xy的值.
参考答案
1--8CDDCD DBB
9.
10.216
11.=
12.3或4或5.
13.灵活性.
14.(1)解:如图①所示,连接一组不相邻的顶点即可;
(2)解:如图②所示,在一边上找一点,分别跟与这条边不相邻的两个顶点相连即可;
(3)解:如图③所示,在四边形内取一点,分别与四个顶点相连即可;
15.(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,
可以把这个五边形分成5-2=3个三角形;
若是一个六边形,可以分割成6-2=4个三角形;
……,依次类推,
n边形可以分割成(n-2)个三角形.
故答案为:3,4,(n-2);
(2) n边形共有n条边,n个顶点,将n边形任意一条边的两顶点与点P相连,得到的三角形是唯一的,故可知此多边形被分割为n个三角形;
(3) 若点P取在多边形的一条边上(不是顶点),再将P与n边形各顶点连接起来,则可将多边形分割成(n-1)个三角形.
16.解:(1)经过A点可以做 1条对角线;同样,经过B点可以做 1条;经过C点可以做 1条;经过D点可以做 1条对角线.
通过以上分析和总结,图1共有 2条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有 5条对角线;
图3共有 9条对角线;
(3)探索归纳:
图1有2条对角线,而
图2共有 5条对角线;而
图3共有 9条对角线;而
归纳可得:
对于边形(n>3),共有条对角线.
(4)特例验证:
当时,
十边形有对角线.
故答案为:(1)2;(2)5、9;(3);(4)35.
17.解:(1)根据题图可知,网格中每个小正方形的边长为1,阴影部分可以拼成一个底边是4,高是3的等腰三角形,
则;
(2)由题意得,,
,
,
的整数部分和小数部分分别是和,
,,
.
一、单选题
1.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )
A.0根 B.1根 C.2根 D.5根
2.一个多边形从一个顶点最多能引出四条对角线,这个多边形是( )
A.四角形 B.五边形 C.六边形 D.七边形
3.若边形恰好有条对角线,则为( )
A.4 B.5 C.6 D.7
4.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成6个三角形,那么这个多边形是( )
A.6边形 B.7边形 C.8边形 D.9边形
5.一个四边形截去一个角后内角个数是( )
A.3 B.4 C.5 D.3、4、5
6.下列命题正确的是( )
A.各边相等的多边形是正多边形
B.各内角分别相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边形是正多边形
D.各边相等、各角也相等的多边形是正多边形
7.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成2011个三角形,那么这个多边形是 ( )
A.2012边形 B.2013边形 C.2014边形 D.2015边形
8.如图,在边长为的小正方形网格中,小正方形的顶点叫格点,以格点为顶点的多边形叫格点多边形图中①,②,③,④四个格点多边形的面积分别记为下列说法正确的是( )
A. B. C. D.
二、填空题
9.一个正八边形,从它的一个顶点可引出m条对角线,并把这个正八边形分成n个三角形,则 .
10.过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则 .
11.如图所示的网格是正方形网格,点A,B,C,D是网格线交点,则的面积与的面积大小关系为: (填“>”“=”或“<”),
12.把一张长方形纸片剪去一个角后,还剩 个角.
13.如图,伸缩晾衣架利用的几何原理是四边形的 .
三、解答题
14.画图题:
(1)如图①从多边形的一个顶点出发画对角线,把多边形分割成三角形;
(2)如图②从多边形的一条边上的一点出发画对角线,把多边形分割成三角形;
(3)如图③从多边形的内部一点出发画对角线,把多边形分割成三角形.
15. (1) 从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成_______个三角形.若是一个六边形,可以分割成_______个三角形.n边形可以分割成______个三角形.
(2)若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?
(3)若点P取在多边形的一条边上(不是顶点),再将P与n边形各顶点连接起来,则可将多边形分割成多少个三角形?
16.探究归纳题:
(1)试验分析:
如图1,经过A点可以作1条对角线;同样,经过B点可以作1条对角线;经过C点可以作1条对角线;经过D点可以作1条对角线.通过以上分析和总结,图1共有________条对角线;
(2)拓展延伸:运用(1)的分析方法,可得:图2共有________条对角线;图3共有________条对角线;
(3)探索归纳:对于n边形(n>3),共有________条对角线;(用含n的式子表示)
(4)特例验证:十边形有________对角线.
17.如图,网格中每个小正方形的边长为1.
(1)求阴影部分的面积;
(2)把图中阴影部分通过剪拼形成一个正方形,设正方形的边长为a.已知a的整数部分和小数部分分别是x和y,求xy的值.
参考答案
1--8CDDCD DBB
9.
10.216
11.=
12.3或4或5.
13.灵活性.
14.(1)解:如图①所示,连接一组不相邻的顶点即可;
(2)解:如图②所示,在一边上找一点,分别跟与这条边不相邻的两个顶点相连即可;
(3)解:如图③所示,在四边形内取一点,分别与四个顶点相连即可;
15.(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,
可以把这个五边形分成5-2=3个三角形;
若是一个六边形,可以分割成6-2=4个三角形;
……,依次类推,
n边形可以分割成(n-2)个三角形.
故答案为:3,4,(n-2);
(2) n边形共有n条边,n个顶点,将n边形任意一条边的两顶点与点P相连,得到的三角形是唯一的,故可知此多边形被分割为n个三角形;
(3) 若点P取在多边形的一条边上(不是顶点),再将P与n边形各顶点连接起来,则可将多边形分割成(n-1)个三角形.
16.解:(1)经过A点可以做 1条对角线;同样,经过B点可以做 1条;经过C点可以做 1条;经过D点可以做 1条对角线.
通过以上分析和总结,图1共有 2条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有 5条对角线;
图3共有 9条对角线;
(3)探索归纳:
图1有2条对角线,而
图2共有 5条对角线;而
图3共有 9条对角线;而
归纳可得:
对于边形(n>3),共有条对角线.
(4)特例验证:
当时,
十边形有对角线.
故答案为:(1)2;(2)5、9;(3);(4)35.
17.解:(1)根据题图可知,网格中每个小正方形的边长为1,阴影部分可以拼成一个底边是4,高是3的等腰三角形,
则;
(2)由题意得,,
,
,
的整数部分和小数部分分别是和,
,,
.
