直线平行的条件[下学期]
文档属性
| 名称 | 直线平行的条件[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 254.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-24 08:33:00 | ||
图片预览


文档简介
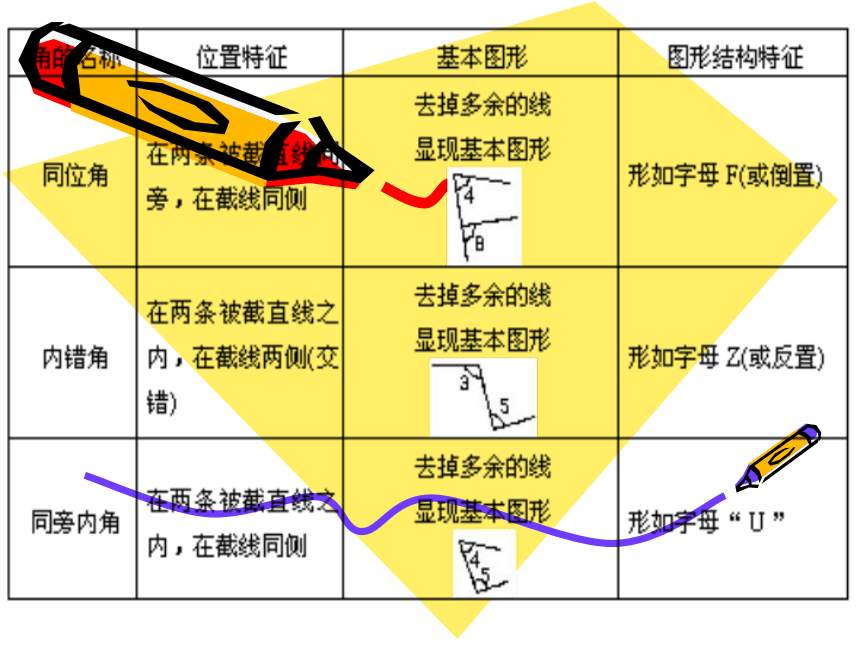
课件20张PPT。直线平行的条件界首四中复习回顾1 同位角定义,内错角定义
2 同位角相等,两直线平行.
3 内错角相等,两直线平行.
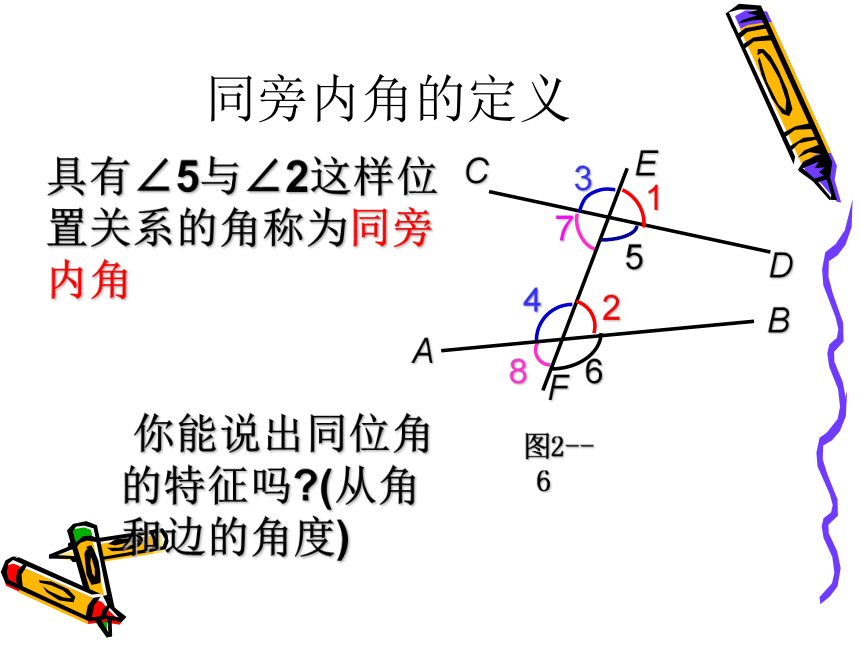
三线八角中还有什么位置关系的角?同旁内角的定义具有∠5与∠2这样位置关系的角称为同旁内角 你能说出同位角的特征吗?(从角和边的角度)
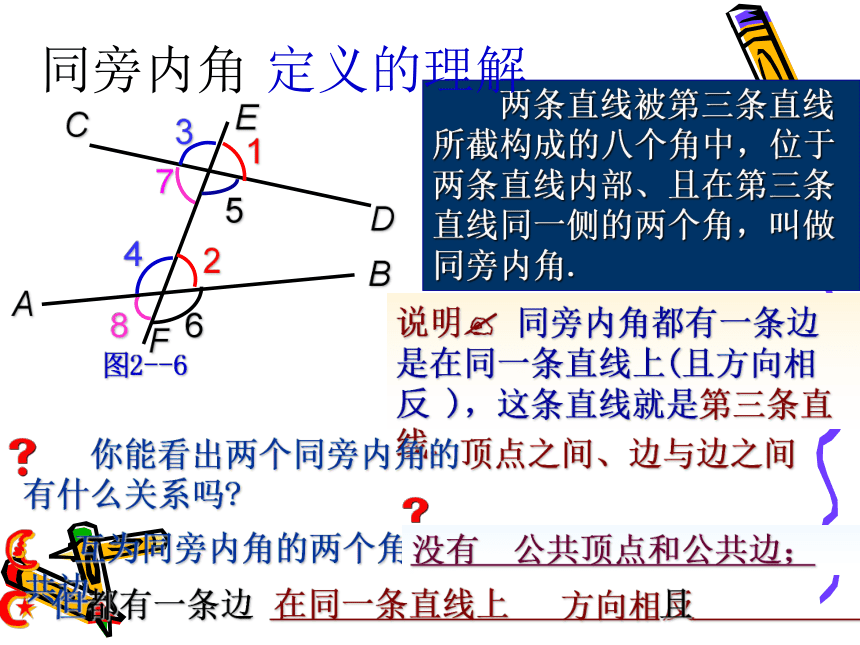
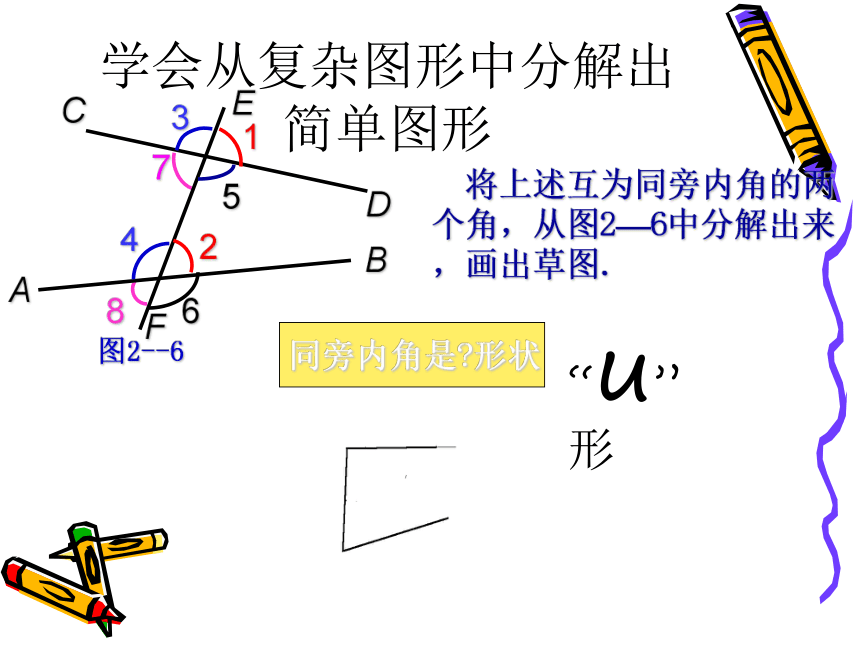
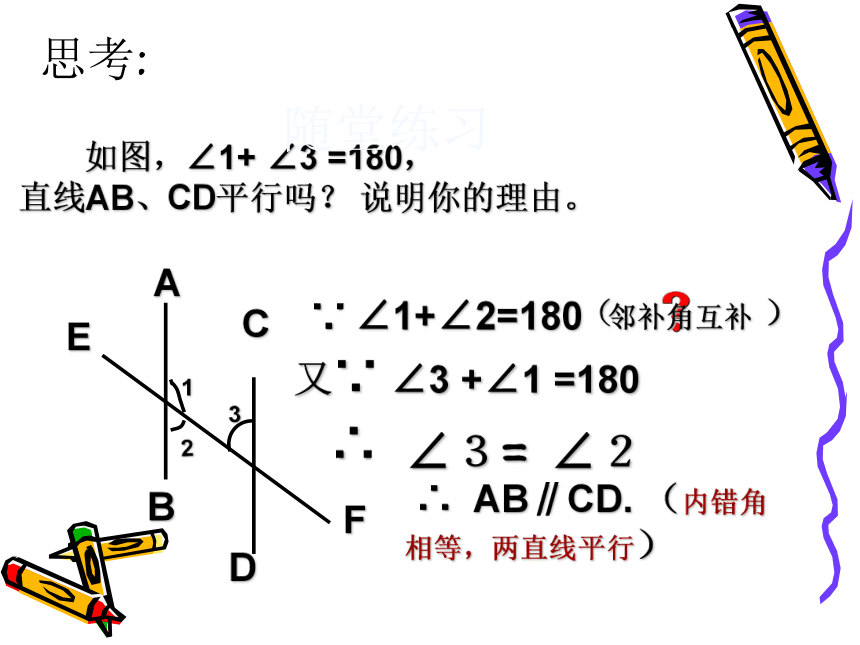
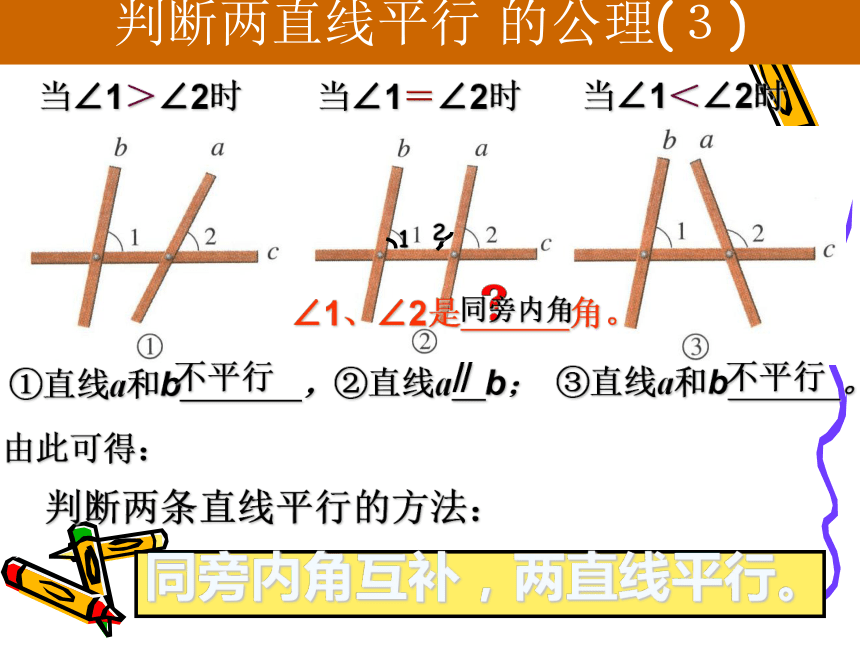
说明? 同旁内角都有一条边是在同一条直线上(且方向相反 ),这条直线就是第三条直线. 两条直线被第三条直线所截构成的八个角中,位于两条直线内部、且在第三条直线同一侧的两个角,叫做同旁内角.同旁内角 定义的理解在同一条直线上 方向相反 没有 公共顶点和公共边;学会从复杂图形中分解出简单图形 将上述互为同旁内角的两个角,从图2—6中分解出来,画出草图.“u”形 如图,∠1+ ∠3 =180,
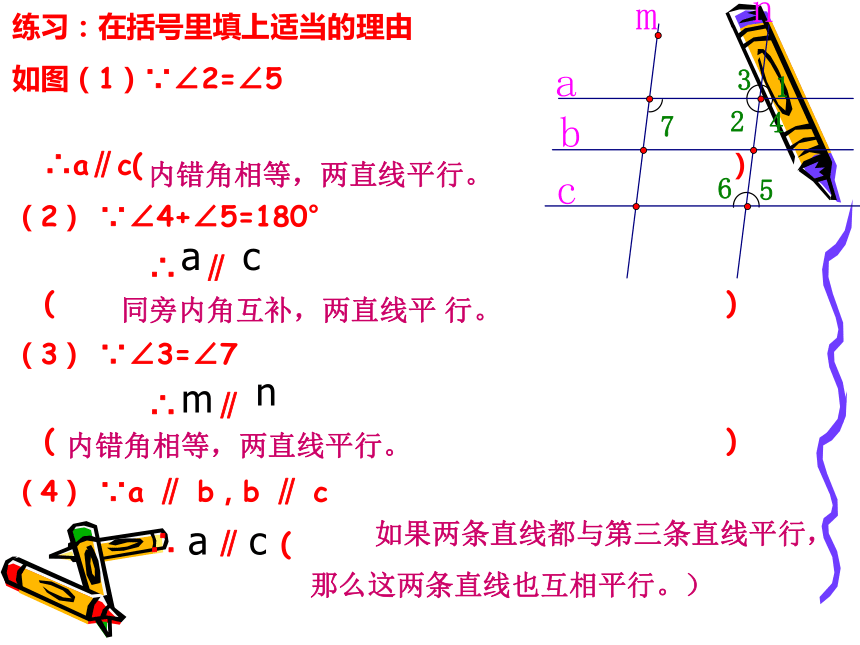
直线AB、CD平行吗? 说明你的理由。ABFCDE∵ ∠1+∠2=180 又∵ ∠3 +∠1 =180 ∴ AB∥CD. (内错角相等,两直线平行)随堂练习( )邻补角互补思考:∴∠3= ∠2123判断两条直线平行的方法:回到两直线平行的判断上来不平行∥不平行由此可得:判断两直线平行 的公理(3)同旁内角21练习:在括号里填上适当的理由
如图(1)∵∠2=∠5
∴a∥c( )
(2) ∵∠4+∠5=180°
∴ ∥ ( )
(3) ∵∠3=∠7
∴ ∥ ( )
(4) ∵a ∥ b,b ∥ c
∴ ∥ ( 内错角相等,两直线平行。同旁内角互补,两直线平 行。内错角相等,两直线平行。 如果两条直线都与第三条直线平行,
那么这两条直线也互相平行。)acmnac练一练1、∵∠1=∠4(已知)
∴ ∥ ( )2、∵∠ABC +∠ =180(已知)
∴AB∥CD( )3、∵∠ =∠ (已知)
∴AD∥BC( )4、∵∠5=∠ (已知)
∴AB∥CD( )5.如图,∠BAC和∠ACD是? [? ]
A.同位角??B.同旁内角
C.内错角??D.以上结论都不对6.如图,共有同旁内角____对 [??]
A.2?? B.3???C.4?? D.5
7、指出图中,
①∠2和∠5的关系是______;
②∠3和∠5的关系是______;
③∠2和______是直线______、______被______所截,形成的同位角;
④∠1和∠4呢?∠3和∠4呢?
∠6和∠7是对顶角吗?8、如图,如果?1=?4,那么AB是否和CD平行,说明你的理由。∵∠1=∠2( )
∠1=∠4( )
∴ ∠4=∠2
∴AB∥CD( )12、如图,a∥c,∠1=∠2,那么c∥b吗?解:∵ ∠1=∠2( )∴ a∥b( ) ∵ a∥c( )∴ c∥b( )13、如图,a、b、c、d是直线,E、F、G、H是交点,
(1)若∠1=∠2,可以证明a∥b,而不能证明c∥d.这是因为∠1和∠2是直线_______和_____被直线____所截而成,它们与直线____无关.
(2)同样的道理,若已知∠1 = ∠3,可以证明______∥______,这是因为它们是直线____和______被直线______所截而成.
探索:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?∵ a⊥b
∴∠1=90 °
又∵ c ⊥ a
∴∠2=90 °∴ ∠1= ∠2
∴b∥c
如图:a ⊥ b,c ⊥ a求证:b∥c结论:
垂直于同一条直线的两条直线互相平行举例1、如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,试指出图中有哪些平行线,说明理由。3、如图,∠BAM+∠AMD=180,∠1=∠2,找出图中平行的直线,并说明理由。
4、如图,如果要判断AB∥CD,你认为还要再添加什么条件?写出这个条件,并说明理由。(用三种不同方法做。)5、如图,如何判断这块玻璃板的上下两边是否平行? 6、如图2-47,一个弯形管道ABCD的拐角∠ABC=110°,∠BCD=70°,这时管道AB、CD平行吗?
2 同位角相等,两直线平行.
3 内错角相等,两直线平行.
三线八角中还有什么位置关系的角?同旁内角的定义具有∠5与∠2这样位置关系的角称为同旁内角 你能说出同位角的特征吗?(从角和边的角度)
说明? 同旁内角都有一条边是在同一条直线上(且方向相反 ),这条直线就是第三条直线. 两条直线被第三条直线所截构成的八个角中,位于两条直线内部、且在第三条直线同一侧的两个角,叫做同旁内角.同旁内角 定义的理解在同一条直线上 方向相反 没有 公共顶点和公共边;学会从复杂图形中分解出简单图形 将上述互为同旁内角的两个角,从图2—6中分解出来,画出草图.“u”形 如图,∠1+ ∠3 =180,
直线AB、CD平行吗? 说明你的理由。ABFCDE∵ ∠1+∠2=180 又∵ ∠3 +∠1 =180 ∴ AB∥CD. (内错角相等,两直线平行)随堂练习( )邻补角互补思考:∴∠3= ∠2123判断两条直线平行的方法:回到两直线平行的判断上来不平行∥不平行由此可得:判断两直线平行 的公理(3)同旁内角21练习:在括号里填上适当的理由
如图(1)∵∠2=∠5
∴a∥c( )
(2) ∵∠4+∠5=180°
∴ ∥ ( )
(3) ∵∠3=∠7
∴ ∥ ( )
(4) ∵a ∥ b,b ∥ c
∴ ∥ ( 内错角相等,两直线平行。同旁内角互补,两直线平 行。内错角相等,两直线平行。 如果两条直线都与第三条直线平行,
那么这两条直线也互相平行。)acmnac练一练1、∵∠1=∠4(已知)
∴ ∥ ( )2、∵∠ABC +∠ =180(已知)
∴AB∥CD( )3、∵∠ =∠ (已知)
∴AD∥BC( )4、∵∠5=∠ (已知)
∴AB∥CD( )5.如图,∠BAC和∠ACD是? [? ]
A.同位角??B.同旁内角
C.内错角??D.以上结论都不对6.如图,共有同旁内角____对 [??]
A.2?? B.3???C.4?? D.5
7、指出图中,
①∠2和∠5的关系是______;
②∠3和∠5的关系是______;
③∠2和______是直线______、______被______所截,形成的同位角;
④∠1和∠4呢?∠3和∠4呢?
∠6和∠7是对顶角吗?8、如图,如果?1=?4,那么AB是否和CD平行,说明你的理由。∵∠1=∠2( )
∠1=∠4( )
∴ ∠4=∠2
∴AB∥CD( )12、如图,a∥c,∠1=∠2,那么c∥b吗?解:∵ ∠1=∠2( )∴ a∥b( ) ∵ a∥c( )∴ c∥b( )13、如图,a、b、c、d是直线,E、F、G、H是交点,
(1)若∠1=∠2,可以证明a∥b,而不能证明c∥d.这是因为∠1和∠2是直线_______和_____被直线____所截而成,它们与直线____无关.
(2)同样的道理,若已知∠1 = ∠3,可以证明______∥______,这是因为它们是直线____和______被直线______所截而成.
探索:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?∵ a⊥b
∴∠1=90 °
又∵ c ⊥ a
∴∠2=90 °∴ ∠1= ∠2
∴b∥c
如图:a ⊥ b,c ⊥ a求证:b∥c结论:
垂直于同一条直线的两条直线互相平行举例1、如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,试指出图中有哪些平行线,说明理由。3、如图,∠BAM+∠AMD=180,∠1=∠2,找出图中平行的直线,并说明理由。
4、如图,如果要判断AB∥CD,你认为还要再添加什么条件?写出这个条件,并说明理由。(用三种不同方法做。)5、如图,如何判断这块玻璃板的上下两边是否平行? 6、如图2-47,一个弯形管道ABCD的拐角∠ABC=110°,∠BCD=70°,这时管道AB、CD平行吗?
