沪科版九年级上册数学第三次月考试卷(含答案)
文档属性
| 名称 | 沪科版九年级上册数学第三次月考试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 253.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 18:29:33 | ||
图片预览


文档简介
沪科版九年级上册数学第三次月考试题
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.的值等于( )
A.1 B. C. D.2
2.抛物线y=x2﹣2x+2的顶点坐标为( )
A.(1,1) B.(﹣1,1) C.(1,3) D.(﹣1,3)
3.点 P 是长度为 1 的线段上的黄金分割点,则较短线段的长度为( )
A. B.3 - C. D.-2
4.若α为锐角,且cosα=0.4,则α的取值范围为( )
A.0°<α<30° B.30°<α<45° C.45°<α<60° D.60°<α<90°
5.若点 A(x1, 6), B (x2,2 ),C(x3,3)在反比例函数的图象上,则 x1,x2,x3的大小关系是( )
A.x1x2x3 B.x3x1x2 C.x2x1x3 D.x3x2x1
6.如图,在菱形 ABCD 中,边长 AB=4,∠A=60°,E、F 为边 BC、CD 的中点,作菱形 CEGF,则图中阴影部分的面积为( )
A.16 B.12 C.8 D.6
7.△ABC 在网格中的位置如图所示(每个小正方形的边长均为 1), AD BC 于 D,下列选项中,错误的是( )
A.sin=cos B.tanC=2 C.tan=1 D.sin=cos
8.已知二次函数 y4x24x1,当自变量x取两个不同的值x1,x2时,函数值相等,则当x取时的函数值为( )
A.-1 B.-2 C.2 D.1
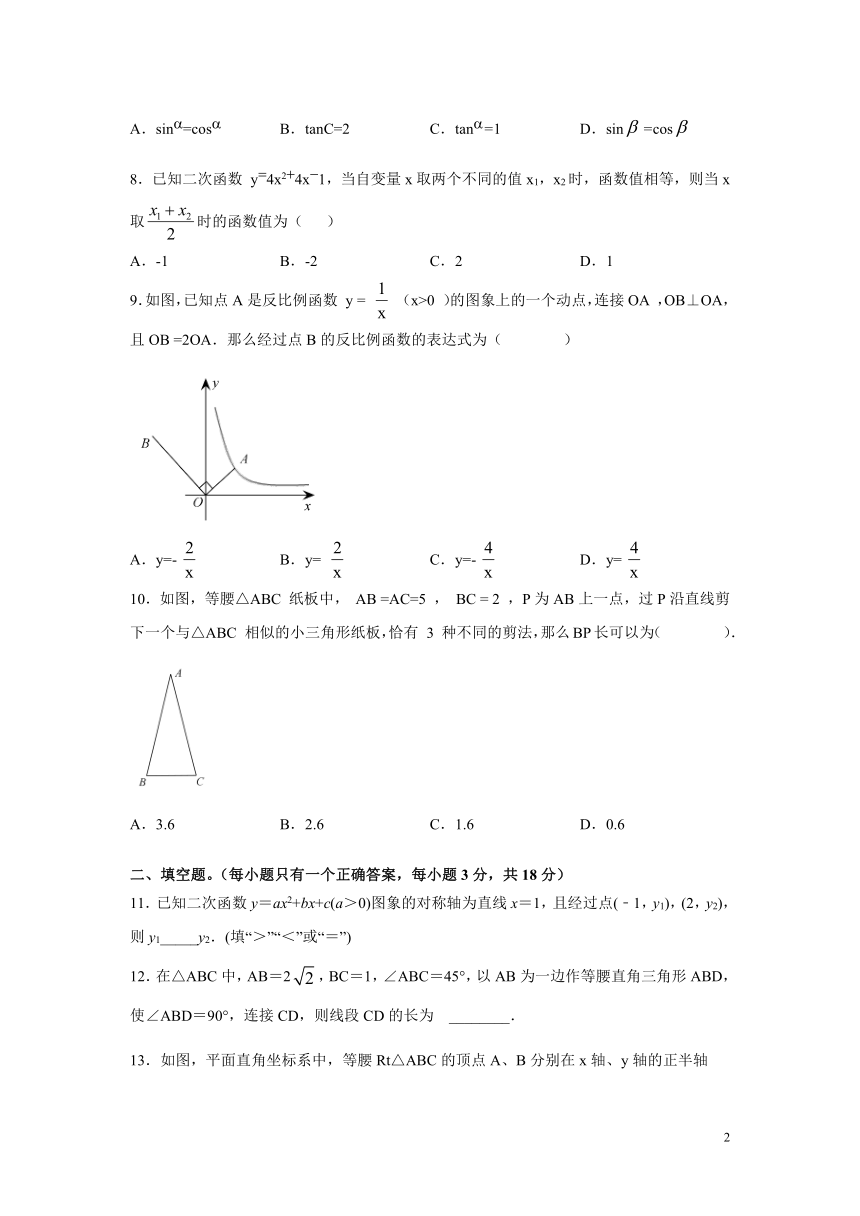
9.如图,已知点A是反比例函数 y = (x>0 )的图象上的一个动点,连接OA ,OB⊥OA,且OB =2OA.那么经过点B的反比例函数的表达式为( )
A.y=- B.y= C.y=- D.y=
10.如图,等腰△ABC 纸板中, AB =AC=5 , BC = 2 ,P为AB上一点,过P沿直线剪下一个与△ABC 相似的小三角形纸板,恰有 3 种不同的剪法,那么BP长可以为( ).
A.3.6 B.2.6 C.1.6 D.0.6
二、填空题。(每小题只有一个正确答案,每小题3分,共18分)
11.已知二次函数y=ax2+bx+c(a>0)图象的对称轴为直线x=1,且经过点(﹣1,y1),(2,y2),则y1_____y2.(填“>”“<”或“=”)
12.在△ABC中,AB=2,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 ________.
13.如图,平面直角坐标系中,等腰Rt△ABC的顶点A、B分别在x轴、y轴的正半轴上,ABC90 , CAx轴,点C在函数y(x0)的图象上.若 AB1,则 k的值为_____.
14.如图,AG:GD4∶1, BD :DC2∶3,则 AE∶EC的值为_____.
15.在Rt△ABC中,∠C=90°,若,则的值为 _______
16.如图,在△ABC中,AD是BC边上的高,若sin C=,BC=12,AC=BD.则△ABC的面积为__________.
三、解答题
17.(8分)计算: 2tan45°- -260°+cos30°
18.(10分)已知:抛物线y=-x2+bx+c经过A(-1,0)、B(5,0)两点,顶点为P.求:
(1)求b,c的值;
(2)求△ABP的面积.
19.(10分)过反比例函数 y= (k < 0)的图象上一点 A 作 x 轴的垂线交 x 轴于点 B ,O 为坐标原点, 且△ABO 的面积 S△ABO = 4 .
(1)求 k 的值;
(2)若二次函数 y = ax2 与反比例函数 y= (k < 0)的图象交于点C(-2,m) ,请结合函数的图象写出满足 ax2< 的x的取值范围.
20.(10分)如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(4,8),B(4,2),C(8,6) .
(1)在第一象限内,画出以原点O 为位似中心,与△ABC 的相似比为的△A1B1C1,并写出 A1,C1点的坐标;
(2)如果△ABC 内部一点P的坐标为 (x, y) ,写出点P在△A1B1C1内的对应点 P1 的坐标.
21.小明在巢湖边“岸上草原”乘坐热气球游玩.他在热气球A上看到前方高楼BC,并测得楼底B点,楼顶C点的俯角分别为45°和22°,已知楼底B与地面在同一水平面上,楼高度为120m.请求出热气球离地面的高度.(参考数据:sin 22°≈0.37,cos22°≈0.93, tan 22°≈0.4)
22.(10分)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥AC于F.
(1)求证:△EDF∽△ADE;
(2)猜想:线段DC、DF、DA之间存在什么关系?并说明理由.
23.(12分)用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形框架ABCD的面积为 3 平方米?
(2)在图②中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
24.(10分)已知:如图,在△ABC 中,D在边AB上.
(1)若∠ACD =∠ABC ,求证:AC2 = AD· AB;
(2)若E为CD 中点,∠ACD =∠ABE,AB = 3,AC=2,求BD的长.
25.(10分)如图,抛物线 y =-x2+3x +4 与x轴负半轴相交于A点,正半轴相交于B点,与 y 轴相交于C 点.
(1)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线 BC 对称的点的坐标;
(2)在(1)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
参考答案
1.A
2.A
3.C
4.D
5.B
6.D
7.D
8.B
9.C
10.D
11.>
12.或
13.1
14.8:5
15.
16.48
17.0.
18.(1)b=4,c=5;(2)27
19.(1)-8;(2)-220.(1)见解析;(2,4),(4,3);(2)(,).
21.热气球到地面的距离约为200米.
22.(1)证明见解析;
(2),理由见解析.
23.(1)当x=1或3米时,矩形框架ABCD的面积为3平方米;(2)当x=时,矩形架ABCD的面积S最大,最大面积是3平方米;(3)当x=时,矩形ABCD的面积S最大,最大面积是平方米.
24.(1)证明见解析;(2).
25.(1)(0,1);(2)(,).
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.的值等于( )
A.1 B. C. D.2
2.抛物线y=x2﹣2x+2的顶点坐标为( )
A.(1,1) B.(﹣1,1) C.(1,3) D.(﹣1,3)
3.点 P 是长度为 1 的线段上的黄金分割点,则较短线段的长度为( )
A. B.3 - C. D.-2
4.若α为锐角,且cosα=0.4,则α的取值范围为( )
A.0°<α<30° B.30°<α<45° C.45°<α<60° D.60°<α<90°
5.若点 A(x1, 6), B (x2,2 ),C(x3,3)在反比例函数的图象上,则 x1,x2,x3的大小关系是( )
A.x1x2x3 B.x3x1x2 C.x2x1x3 D.x3x2x1
6.如图,在菱形 ABCD 中,边长 AB=4,∠A=60°,E、F 为边 BC、CD 的中点,作菱形 CEGF,则图中阴影部分的面积为( )
A.16 B.12 C.8 D.6
7.△ABC 在网格中的位置如图所示(每个小正方形的边长均为 1), AD BC 于 D,下列选项中,错误的是( )
A.sin=cos B.tanC=2 C.tan=1 D.sin=cos
8.已知二次函数 y4x24x1,当自变量x取两个不同的值x1,x2时,函数值相等,则当x取时的函数值为( )
A.-1 B.-2 C.2 D.1
9.如图,已知点A是反比例函数 y = (x>0 )的图象上的一个动点,连接OA ,OB⊥OA,且OB =2OA.那么经过点B的反比例函数的表达式为( )
A.y=- B.y= C.y=- D.y=
10.如图,等腰△ABC 纸板中, AB =AC=5 , BC = 2 ,P为AB上一点,过P沿直线剪下一个与△ABC 相似的小三角形纸板,恰有 3 种不同的剪法,那么BP长可以为( ).
A.3.6 B.2.6 C.1.6 D.0.6
二、填空题。(每小题只有一个正确答案,每小题3分,共18分)
11.已知二次函数y=ax2+bx+c(a>0)图象的对称轴为直线x=1,且经过点(﹣1,y1),(2,y2),则y1_____y2.(填“>”“<”或“=”)
12.在△ABC中,AB=2,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 ________.
13.如图,平面直角坐标系中,等腰Rt△ABC的顶点A、B分别在x轴、y轴的正半轴上,ABC90 , CAx轴,点C在函数y(x0)的图象上.若 AB1,则 k的值为_____.
14.如图,AG:GD4∶1, BD :DC2∶3,则 AE∶EC的值为_____.
15.在Rt△ABC中,∠C=90°,若,则的值为 _______
16.如图,在△ABC中,AD是BC边上的高,若sin C=,BC=12,AC=BD.则△ABC的面积为__________.
三、解答题
17.(8分)计算: 2tan45°- -260°+cos30°
18.(10分)已知:抛物线y=-x2+bx+c经过A(-1,0)、B(5,0)两点,顶点为P.求:
(1)求b,c的值;
(2)求△ABP的面积.
19.(10分)过反比例函数 y= (k < 0)的图象上一点 A 作 x 轴的垂线交 x 轴于点 B ,O 为坐标原点, 且△ABO 的面积 S△ABO = 4 .
(1)求 k 的值;
(2)若二次函数 y = ax2 与反比例函数 y= (k < 0)的图象交于点C(-2,m) ,请结合函数的图象写出满足 ax2< 的x的取值范围.
20.(10分)如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(4,8),B(4,2),C(8,6) .
(1)在第一象限内,画出以原点O 为位似中心,与△ABC 的相似比为的△A1B1C1,并写出 A1,C1点的坐标;
(2)如果△ABC 内部一点P的坐标为 (x, y) ,写出点P在△A1B1C1内的对应点 P1 的坐标.
21.小明在巢湖边“岸上草原”乘坐热气球游玩.他在热气球A上看到前方高楼BC,并测得楼底B点,楼顶C点的俯角分别为45°和22°,已知楼底B与地面在同一水平面上,楼高度为120m.请求出热气球离地面的高度.(参考数据:sin 22°≈0.37,cos22°≈0.93, tan 22°≈0.4)
22.(10分)如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,DE⊥AB于E,EF∥AC于F.
(1)求证:△EDF∽△ADE;
(2)猜想:线段DC、DF、DA之间存在什么关系?并说明理由.
23.(12分)用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形框架ABCD的面积为 3 平方米?
(2)在图②中,如果不锈钢材料总长度为 12 米,当x为多少时,矩形架ABCD的面积S最大?最大面积是多少?
(3)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
24.(10分)已知:如图,在△ABC 中,D在边AB上.
(1)若∠ACD =∠ABC ,求证:AC2 = AD· AB;
(2)若E为CD 中点,∠ACD =∠ABE,AB = 3,AC=2,求BD的长.
25.(10分)如图,抛物线 y =-x2+3x +4 与x轴负半轴相交于A点,正半轴相交于B点,与 y 轴相交于C 点.
(1)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线 BC 对称的点的坐标;
(2)在(1)的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
参考答案
1.A
2.A
3.C
4.D
5.B
6.D
7.D
8.B
9.C
10.D
11.>
12.或
13.1
14.8:5
15.
16.48
17.0.
18.(1)b=4,c=5;(2)27
19.(1)-8;(2)-2
21.热气球到地面的距离约为200米.
22.(1)证明见解析;
(2),理由见解析.
23.(1)当x=1或3米时,矩形框架ABCD的面积为3平方米;(2)当x=时,矩形架ABCD的面积S最大,最大面积是3平方米;(3)当x=时,矩形ABCD的面积S最大,最大面积是平方米.
24.(1)证明见解析;(2).
25.(1)(0,1);(2)(,).
(
2
)
(
1
)
同课章节目录
