沪科版九年级上册数学期中考试试卷(含答案)
文档属性
| 名称 | 沪科版九年级上册数学期中考试试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 229.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览



文档简介
沪科版九年级上册数学期中考试试题
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.若反比例函数y=的图象位于第一、三象限,则k的取值可以是( )
A.﹣3 B.﹣2 C.﹣1 D.0
2.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
3.将抛物线向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )
A. B. C. D.
4.下列命题不一定成立的是( )
A.斜边与一条直角边对应成比例的两个直角三角形相似;
B.两个等腰直角三角形相似;
C.两边对应成比例且有一个角相等的两个三角形相似;
D.各有一个角等于95°的两个等腰三角形相似.
5.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
6.二次函数的图象与轴有交点,则的取值范围是( )
A. B.且 C. D.且
7.如图,点是反比例函数的图象上任意一点,轴交反比例函数的图象于点,以为边作平行四边形,其中,在轴上,则为( )
A.2 B.3 C.4 D.5
8.如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是( )
A. B. C. D.
9.如图,已知二次函数的图象与正比例函数的图象交于点A(3,2),与x轴交于点B(2,0),若,则x的取值范围是( )
A.0<x<2 B.x<0或x>3 C.2<x<3 D.0<x<3
10.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
二、填空题。(每小题3分,共18分)
11.已知,则=_____.
12.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2,该型号飞机着陆后滑行 m才能停下来.
13.一个诺大的舞台,当主持人站在黄金分割点处时,不仅看起开美观,而且音响效果也非常好,若舞台的长度为10米,那么,主持人到较近的一侧应为______米
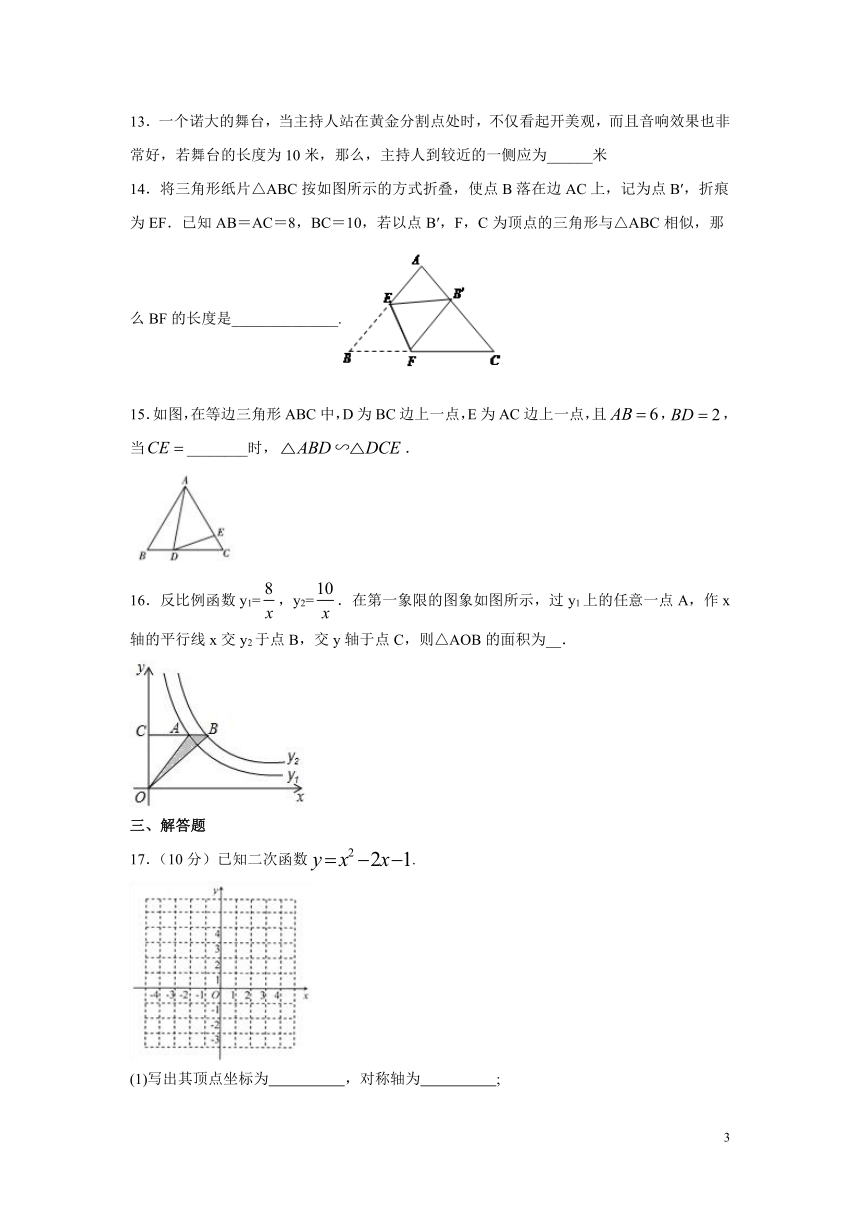
14.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.
15.如图,在等边三角形ABC中,D为BC边上一点,E为AC边上一点,且,,当________时,.
16.反比例函数y1=,y2=.在第一象限的图象如图所示,过y1上的任意一点A,作x轴的平行线x交y2于点B,交y轴于点C,则△AOB的面积为__.
三、解答题
17.(10分)已知二次函数.
(1)写出其顶点坐标为 ,对称轴为 ;
(2)在右边平面直角坐标系内画出该函数图像;
(3)根据图像写出满足的的取值范围 .
18.(5分)若x、y、z满足===k,求k的值.
19.(10分)如图,直线,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
20.(10分)有一个抛物线形的拱形桥洞,桥面离水面的距离为5.6米,桥洞离水面的最大高度为,跨度为, 如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式.
(2)如图,在对称轴右边处,桥洞离桥面的高是多少?
21.(12分)如图,反比例函数 y=的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;
(3)连接AO、BO,求△ABO的面积;
(4)在y轴上存在点P,使△AOP为等腰三角形,请直接写出点P的坐标.
22.(8分)如图,已知:AP2=AQ AB,且∠ABP=∠C,试说明△QPB∽△PBC.
23.(8分)天水“伏羲文化节”商品交易会上,某商人将每件进价为8元的纪念品,按每件9元出售,每天可售出20件.他想采用提高售价的办法来增加利润,经实验,发现这种纪念品每件提价1元,每天的销售量会减少4件.
(1)写出每天所得的利润y(元)与售价x(元/件)之间的函数关系式.
(2)每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?
24.(12分)定义:如图1,D,E在△ABC的边BC上,若△ADE是等边三角形则称△ABC可内嵌,△ADE叫做△ABC的内嵌三角形.
(1)直角三角形______可内嵌.(填写“一定”、“一定不”或“不一定”)
(2)如图2,在△ABC中,∠BAC=120°,△ADE是△ABC的内嵌三角形,试说明AB2=BD BC是否成立?如果成立,请给出证明;如果不一定成立,请举例说明.
(3)在(2)的条件下,如果AB=1,AC=2,求△ABC的内嵌△ADE的边长
25.(12分)如图,一次函数分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
参考答案
1.D
2.D
3.B
4.C
5.A
6.D
7.D
8.D
9.D
10.D
11.
12.600.
13.15-5
14.5或 (答对一个得1分)
15.
16.1
17.(1,-2),直线x=1, x<-1或x>3.
18.k=﹣1;k=2.
19.(1)12;(2)1:2
20.(1)二次函数解析式为;(2)桥洞离桥面的高是1.76米.
21.(1)y=,y=x+2;(2)-3<x<0或x>1;(3)4;(4)P(0,- )或P(0,)或P(0,6)或P(0,).
22.证明见解析.
23.(1)y=﹣4x2+88x﹣448(9≤x≤14);(2)售价为11元时,利润最大,最大利润是36元.
24.(1)不一定;(2)成立,理由见解析;(3)
25.(1)y=﹣x2+x+2(2)当t=2时,MN有最大值4(3)D点坐标为(0,6),(0,﹣2)或(4,4)
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.若反比例函数y=的图象位于第一、三象限,则k的取值可以是( )
A.﹣3 B.﹣2 C.﹣1 D.0
2.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
3.将抛物线向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )
A. B. C. D.
4.下列命题不一定成立的是( )
A.斜边与一条直角边对应成比例的两个直角三角形相似;
B.两个等腰直角三角形相似;
C.两边对应成比例且有一个角相等的两个三角形相似;
D.各有一个角等于95°的两个等腰三角形相似.
5.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
6.二次函数的图象与轴有交点,则的取值范围是( )
A. B.且 C. D.且
7.如图,点是反比例函数的图象上任意一点,轴交反比例函数的图象于点,以为边作平行四边形,其中,在轴上,则为( )
A.2 B.3 C.4 D.5
8.如图,在中,点P在边AB上,则在下列四个条件中::;;;,能满足与相似的条件是( )
A. B. C. D.
9.如图,已知二次函数的图象与正比例函数的图象交于点A(3,2),与x轴交于点B(2,0),若,则x的取值范围是( )
A.0<x<2 B.x<0或x>3 C.2<x<3 D.0<x<3
10.如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
二、填空题。(每小题3分,共18分)
11.已知,则=_____.
12.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2,该型号飞机着陆后滑行 m才能停下来.
13.一个诺大的舞台,当主持人站在黄金分割点处时,不仅看起开美观,而且音响效果也非常好,若舞台的长度为10米,那么,主持人到较近的一侧应为______米
14.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.
15.如图,在等边三角形ABC中,D为BC边上一点,E为AC边上一点,且,,当________时,.
16.反比例函数y1=,y2=.在第一象限的图象如图所示,过y1上的任意一点A,作x轴的平行线x交y2于点B,交y轴于点C,则△AOB的面积为__.
三、解答题
17.(10分)已知二次函数.
(1)写出其顶点坐标为 ,对称轴为 ;
(2)在右边平面直角坐标系内画出该函数图像;
(3)根据图像写出满足的的取值范围 .
18.(5分)若x、y、z满足===k,求k的值.
19.(10分)如图,直线,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
20.(10分)有一个抛物线形的拱形桥洞,桥面离水面的距离为5.6米,桥洞离水面的最大高度为,跨度为, 如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式.
(2)如图,在对称轴右边处,桥洞离桥面的高是多少?
21.(12分)如图,反比例函数 y=的图象与一次函数y=mx+b的图象交于两点A(1,3),B(n,-1).
(1)求反比例函数与一次函数的函数关系式;
(2)根据图象,直接回答:当x取何值时,一次函数的值大于反比例函数的值;
(3)连接AO、BO,求△ABO的面积;
(4)在y轴上存在点P,使△AOP为等腰三角形,请直接写出点P的坐标.
22.(8分)如图,已知:AP2=AQ AB,且∠ABP=∠C,试说明△QPB∽△PBC.
23.(8分)天水“伏羲文化节”商品交易会上,某商人将每件进价为8元的纪念品,按每件9元出售,每天可售出20件.他想采用提高售价的办法来增加利润,经实验,发现这种纪念品每件提价1元,每天的销售量会减少4件.
(1)写出每天所得的利润y(元)与售价x(元/件)之间的函数关系式.
(2)每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?
24.(12分)定义:如图1,D,E在△ABC的边BC上,若△ADE是等边三角形则称△ABC可内嵌,△ADE叫做△ABC的内嵌三角形.
(1)直角三角形______可内嵌.(填写“一定”、“一定不”或“不一定”)
(2)如图2,在△ABC中,∠BAC=120°,△ADE是△ABC的内嵌三角形,试说明AB2=BD BC是否成立?如果成立,请给出证明;如果不一定成立,请举例说明.
(3)在(2)的条件下,如果AB=1,AC=2,求△ABC的内嵌△ADE的边长
25.(12分)如图,一次函数分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
参考答案
1.D
2.D
3.B
4.C
5.A
6.D
7.D
8.D
9.D
10.D
11.
12.600.
13.15-5
14.5或 (答对一个得1分)
15.
16.1
17.(1,-2),直线x=1, x<-1或x>3.
18.k=﹣1;k=2.
19.(1)12;(2)1:2
20.(1)二次函数解析式为;(2)桥洞离桥面的高是1.76米.
21.(1)y=,y=x+2;(2)-3<x<0或x>1;(3)4;(4)P(0,- )或P(0,)或P(0,6)或P(0,).
22.证明见解析.
23.(1)y=﹣4x2+88x﹣448(9≤x≤14);(2)售价为11元时,利润最大,最大利润是36元.
24.(1)不一定;(2)成立,理由见解析;(3)
25.(1)y=﹣x2+x+2(2)当t=2时,MN有最大值4(3)D点坐标为(0,6),(0,﹣2)或(4,4)
(
2
)
(
1
)
同课章节目录
