人教B版高中数学必修第四册11.2 平面的基本事实与推论 课件(共41张PPT)
文档属性
| 名称 | 人教B版高中数学必修第四册11.2 平面的基本事实与推论 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 969.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览







文档简介
(共41张PPT)
11.2 平面的基本事实与推论
新知初探·自主学习
课堂探究·素养提升
课程标准
1.借助长方体,了解以下基本事实和推论.
基本事实1:经过不在一条直线上的3个点,有且只有一个平面.
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
2.能用已获得的结论证明空间基本图形位置关系的简单命题.
3.重点提升直观想象、逻辑推理、数学运算和数学抽象素养.
新知初探·自主学习
教 材 要 点
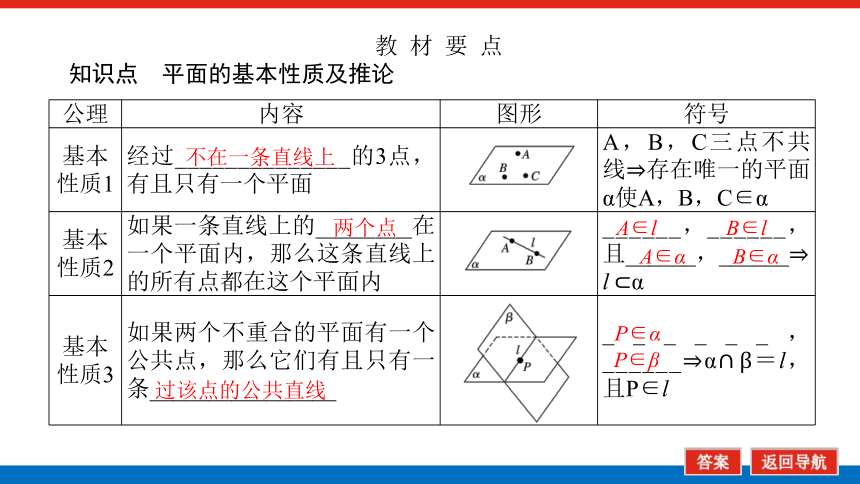
知识点 平面的基本性质及推论
公理 内容 图形 符号
基本性质1 经过______________的3点,有且只有一个平面 A,B,C三点不共线 存在唯一的平面α使A,B,C∈α
基本性质2 如果一条直线上的________在一个平面内,那么这条直线上的所有点都在这个平面内 ______,______,且______,______ l α
基本性质3 如果两个不重合的平面有一个公共点,那么它们有且只有一条________________ ______,______ α=l,且P∈l
不在一条直线上
两个点
A∈l
B∈l
A∈α
B∈α
过该点的公共直线
P∈α
P∈β
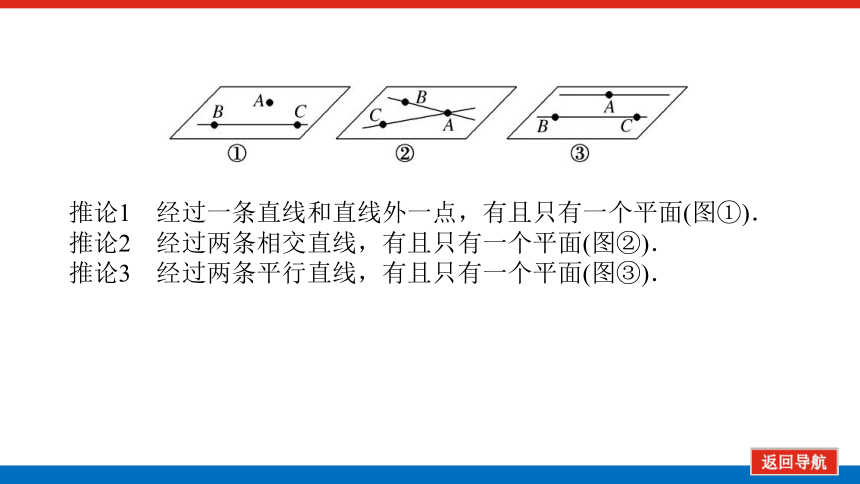
推论1 经过一条直线和直线外一点,有且只有一个平面(图①).
推论2 经过两条相交直线,有且只有一个平面(图②).
推论3 经过两条平行直线,有且只有一个平面(图③).
基 础 自 测
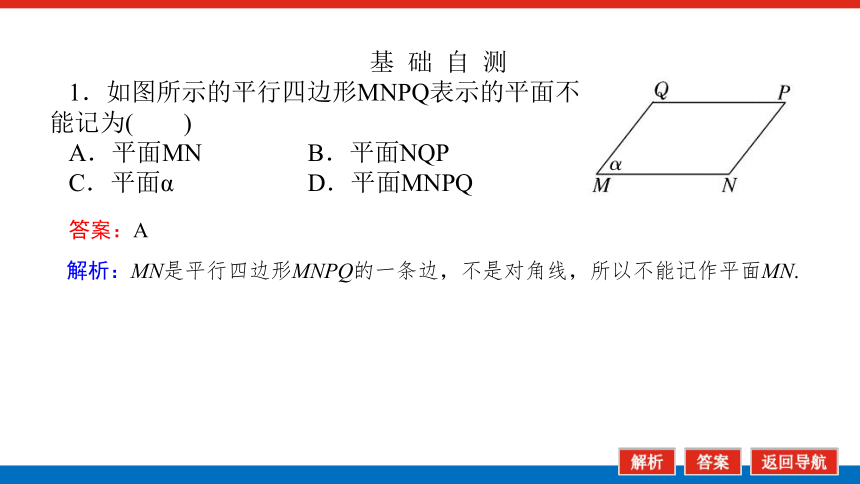
1.如图所示的平行四边形MNPQ表示的平面不
能记为( )
A.平面MN B.平面NQP
C.平面α D.平面MNPQ
答案:A
解析:MN是平行四边形MNPQ的一条边,不是对角线,所以不能记作平面MN.
2.能确定一个平面的条件是( )
A.空间三个点 B.一个点和一条直线
C.无数个点 D.两条相交直线
答案:D
解析:不在同一条直线上的三个点可确定一个平面,A,B,C条件不能保证有不在同一条直线上的三个点,故不正确.
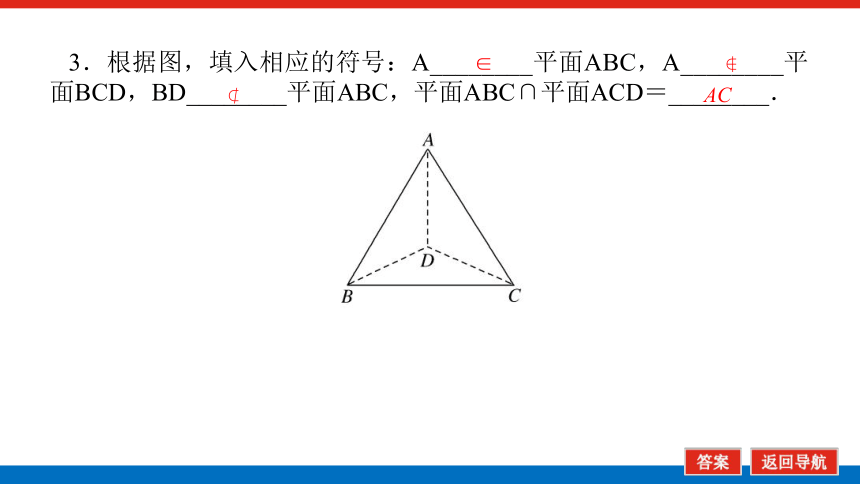
3.根据图,填入相应的符号:A________平面ABC,A________平面BCD,BD________平面ABC,平面ABC∩平面ACD=________.
∈
AC
4.下列说法正确的是( )
A.两个平面可以有且仅有一个公共点
B.梯形一定是平面图形
C.平面α和β有不同在一条直线上的三个交点
D.一条直线和一个点确定一个平面
答案:B
解析:A选项,根据基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,故A错.C选项,两个平面有公共点,则有一条过该公共点的公共直线,如果没有公共点,则两平面平行,C错.D选项,一条直线和直线外的一点可以确定一个平面,D错.B选项,两条平行直线,确定一个平面,梯形中有一组对边平行,故B对.
课堂探究·素养提升
题型1 文字语言、图形语言、符号语言的相互转化
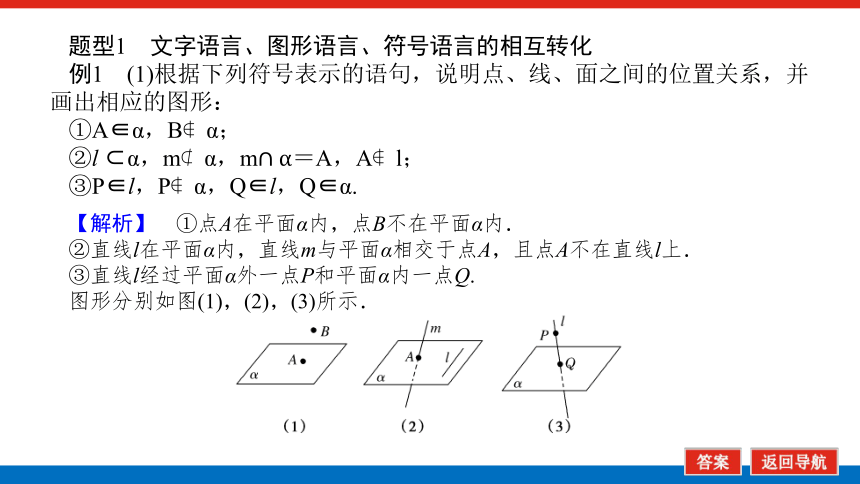
例1 (1)根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
①A∈α,B α;
②l α,m α,m=A,A l;
③P∈l,P α,Q∈l,Q∈α.
【解析】 ①点A在平面α内,点B不在平面α内.
②直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上.
③直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.
(2)如图所示,用符号语言可表达为( )
A.α=m,n α,A m,A n
B.α=m,n∈α,A∈m,A∈n
C.α=m,n α,m=A
D.α=m,n∈α,m=A
【答案】 C
【解析】 结合图形可以得出平面α,β相交于一条直线m,直线n在平面α内,直线m,n相交于点A,点A在直线m,n上,结合选项可得C正确.
方法归纳
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“ ”表示,直线与平面的位置关系只能用“ ”或“ ”表示.
(3)由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
跟踪训练1 (1)如图,根据图形用符号表示下列点、直线、平面之间的关系.
①点P与直线AB;
②点C与直线AB;
③点M与平面AC;
④点A1与平面AC;
⑤直线AB与直线BC;
⑥直线AB与平面AC;
⑦平面A1B与平面AC.
解析:①点P∈直线AB;②点C 直线AB;
③点M∈平面AC;④点A1 平面AC;
⑤直线AB∩直线BC=点B;⑥直线AB 平面AC;
⑦平面A1B∩平面AC=直线AB.
(2)若点A在平面α内,直线a在平面α内,点A不在直线a上,用符号语言可表示为( )
A.A∈α,a α,A a
B.A∈α,a∈α,A a
C.A α,a α,A a
D.A∈α,a α,A a
答案:A
解析:点与线、面的关系用∈、 ;线与面的关系用 、 .B项中,“a∈α”错;C项中“A α”错;D项中“A a”错.
题型2 点、线共面问题
例2 (1)已知四条直线两两相交,且不共点,求证:这四条直线在同一平面内;
【解析】 已知:a,b,c,d四条直线两两相交,且不共点,求证:a,b,c,d四线共面.
证明:①若a,b,c三线共点于O,如图所示,∵O d,
∴经过d与点O有且只有一个平面α.
∵A,B,C分别是d与a,b,c的交点,
∴A,B,C三点在平面α内.
由公理1知a,b,c都在平面α内,
故a,b,c,d共面.
②若a,b,c,d无三线共点,如图所示,
∵a=A,
∴经过a,b有且仅有一个平面α,
∴B,C∈α.由公理1知c α.
同理,d α,从而有a,b,c,d共面.
综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.
(2)空间两两相交的三条直线,可以确定的平面数是( )
A.1 B.2
C.3 D.1或3
答案:D
解析:若三条直线两两相交共有三个交点,则确定1个平面;若三条直线两两相交且交于同一点时,若三条直线共面,则能确定1个平面,若三条直线不共面,则能确定3个平面.
状元随笔 四条直线两两相交且不共点,可能有两种情况:一是有三条直线共点;二是任意三条直线都不共点,故要分两种情况.
方法归纳
证明点线共面常用的方法
(1)纳入法:先由部分直线确定一个平面,再证明其他直线也在这个平面内.
(2)重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.
跟踪训练2 (1)一条直线与三条平行直线都相交,求证:这四条直线共面.
(2)如图所示,在正方体ABCD - A1B1C1D1中.
①AA1与CC1是否在同一平面内?
②点B,C1,D是否在同一平面内?
③画出平面ACC1A1与平面BC1D及平面ACD1与平面BDC1的交线.
解析:(1)已知:a∥b∥c,l=A,l=B,l=C.
求证:直线a,b,c,l共面.
证明:证法一:∵a∥b,∴a,b确定一个平面α,
∵l=A,l=B,∴A∈α,B∈α,故l α.
又∵a∥c,∴a,c确定一个平面β.
同理可证l β,∴α=a且α=l.
∵过两条相交直线a、l有且只有一个平面,
故α与β重合,即直线a,b,c,l共面.
证法二:由证法一得a、b、l共面α,也就是说b在a、l确定的平面α内.
同理可证c在a、l确定的平面α内.
∵过a和l只能确定一个平面,∴a,b,c,l共面.
(2)①在正方体ABCD - A1B1C1D1中,
因为AA1∥CC1,所以AA1与CC1可确定平面AC1,
所以AA1与CC1在同一平面内.
②因为点B,C1,D不共线,所以点B,C1,D可确定平面BC1D,所以点B,C1,D在同一平面内.
③如图,因为AC=O,D1C=E,
所以O∈平面AC1,O∈平面BC1D.
又C1∈平面AC1,C1∈平面BC1D.
所以平面AC1∩平面BC1D=OC1.
同理平面ACD1∩平面BDC1=OE.
题型3 点共线与线共点问题
【思考探究】 1.如图,在正方体ABCD - A1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面内?
[提示] 如图,连接BD1,
∵A1C∩平面ABC1D1=E,
∴E∈A1C,E∈平面ABC1D1.
∵A1C 平面A1BCD1,
∴E∈平面A1BCD1.
2.上述问题中,你能证明B,E,D1三点共线吗?
[提示] 由于平面A1BCD1与平面ABC1D1交于直线BD1,又E∈BD1,根据公理3可知B,E,D1三点共线.
例3 在正方体ABCD - A1B1C1D1中,E,F分别是AA1,AB的中点.
(1)证明:点E,F,C,D1共面;
(2)证明:D1E,DA,CF三线交于一点.
【证明】 (1)连接A1B,根据正方体的几何性质可知A1B∥CD1.由于E,F分别是AA1,AB的中点,所以EF∥A1B,
所以EF∥CD1,所以E,F,C,D1四点共面.
(2)由于EF∥CD1,EF≠CD1,所以D1E与CF延长后必相交,设交点为P,由于P∈D1E,D1E 平面ADD1A1,P∈CF,CF 平面ABCD,根据基本事实3可知P在平面ADD1A1与平面ABCD的交线DA上,所以D1E,DA,CF三线交于一点.
方法归纳
点共线与线共点的证明方法
(1)点共线:证明多点共线通常利用公理3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.
(2)三线共点:证明三线共点问题可把其中一条直线作为分别过其余两条直线的两个平面的交线,然后再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.
跟踪训练3
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别为边AB,BC上的点,且==.
求证:(1)点E,F,G,H四点共面;
(2)直线EH,BD,FG相交于同一点.
证明:(1)如图所示,连接EF,HG,在空间四边形ABCD中,H,G分别是AD,CD的中点,
所以HG∥AC且HG=AC.
又==,所以EF∥AC且EF=AC.
故EF∥HG,即E,F,G,H四点共面.
(2)由(1)知EF∥HG且EF≠HG,
所以设EH与FG交于点P,因为EH 平面ABD,所以P在平面ABD内,同理P在平面BCD内,且平面ABD∩平面BCD=BD,
所以点P在直线BD上,
所以直线EH,BD,FG相交于一点.
题型4 由平面的基本性质做截面图形
例4 如图所示,G是正方体ABCD - A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC;
(2)过三点E,F,D1.
【解析】 (1)连接GA交A1D1于点M,连接GC交C1D1于点N,从而可以得到过点G及AC的平面.
画法:连接GA交A1D1于点M,连接GC交C1D1于点N;
连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.
(2)根据两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,即可作出交线.
画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;
连接D1P交CC1于点M,连接D1Q交AA1于点N;
连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.
方法归纳
解决几何体的截面问题的基本方法
(1)直接法
用直接法解决截面问题的关键是:截面上的点在几何体的棱上,且两两在一个平面内,我们可以借助于基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内,直接解决这类问题.
(2)延长线法
用延长线法解决截面问题的关键是:截面上的点中至少有两个点在一个几何体的一个表面上,我们可以借助于基本事实2,如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.直接解决这类问题.
跟踪训练4 (1)如图,在正方体ABCD - A1B1C1D1中,试画出平面AB1D1与平面ACC1A1的交线.
解析:记B1D1与A1C1的交点为O,连接AO,则AO即为平面AB1D1与平面ACC1A1的交线,如图:
(2)如图,直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABCD所在平面外一点,画出平面SBD和平面SAC的交线.
解析:延长BD和AC交于点O,连接SO,SO即为平面SBD和平面SAC的交线,如图:
11.2 平面的基本事实与推论
新知初探·自主学习
课堂探究·素养提升
课程标准
1.借助长方体,了解以下基本事实和推论.
基本事实1:经过不在一条直线上的3个点,有且只有一个平面.
基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.
基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
2.能用已获得的结论证明空间基本图形位置关系的简单命题.
3.重点提升直观想象、逻辑推理、数学运算和数学抽象素养.
新知初探·自主学习
教 材 要 点
知识点 平面的基本性质及推论
公理 内容 图形 符号
基本性质1 经过______________的3点,有且只有一个平面 A,B,C三点不共线 存在唯一的平面α使A,B,C∈α
基本性质2 如果一条直线上的________在一个平面内,那么这条直线上的所有点都在这个平面内 ______,______,且______,______ l α
基本性质3 如果两个不重合的平面有一个公共点,那么它们有且只有一条________________ ______,______ α=l,且P∈l
不在一条直线上
两个点
A∈l
B∈l
A∈α
B∈α
过该点的公共直线
P∈α
P∈β
推论1 经过一条直线和直线外一点,有且只有一个平面(图①).
推论2 经过两条相交直线,有且只有一个平面(图②).
推论3 经过两条平行直线,有且只有一个平面(图③).
基 础 自 测
1.如图所示的平行四边形MNPQ表示的平面不
能记为( )
A.平面MN B.平面NQP
C.平面α D.平面MNPQ
答案:A
解析:MN是平行四边形MNPQ的一条边,不是对角线,所以不能记作平面MN.
2.能确定一个平面的条件是( )
A.空间三个点 B.一个点和一条直线
C.无数个点 D.两条相交直线
答案:D
解析:不在同一条直线上的三个点可确定一个平面,A,B,C条件不能保证有不在同一条直线上的三个点,故不正确.
3.根据图,填入相应的符号:A________平面ABC,A________平面BCD,BD________平面ABC,平面ABC∩平面ACD=________.
∈
AC
4.下列说法正确的是( )
A.两个平面可以有且仅有一个公共点
B.梯形一定是平面图形
C.平面α和β有不同在一条直线上的三个交点
D.一条直线和一个点确定一个平面
答案:B
解析:A选项,根据基本事实3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,故A错.C选项,两个平面有公共点,则有一条过该公共点的公共直线,如果没有公共点,则两平面平行,C错.D选项,一条直线和直线外的一点可以确定一个平面,D错.B选项,两条平行直线,确定一个平面,梯形中有一组对边平行,故B对.
课堂探究·素养提升
题型1 文字语言、图形语言、符号语言的相互转化
例1 (1)根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
①A∈α,B α;
②l α,m α,m=A,A l;
③P∈l,P α,Q∈l,Q∈α.
【解析】 ①点A在平面α内,点B不在平面α内.
②直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上.
③直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.
(2)如图所示,用符号语言可表达为( )
A.α=m,n α,A m,A n
B.α=m,n∈α,A∈m,A∈n
C.α=m,n α,m=A
D.α=m,n∈α,m=A
【答案】 C
【解析】 结合图形可以得出平面α,β相交于一条直线m,直线n在平面α内,直线m,n相交于点A,点A在直线m,n上,结合选项可得C正确.
方法归纳
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“ ”表示,直线与平面的位置关系只能用“ ”或“ ”表示.
(3)由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.
跟踪训练1 (1)如图,根据图形用符号表示下列点、直线、平面之间的关系.
①点P与直线AB;
②点C与直线AB;
③点M与平面AC;
④点A1与平面AC;
⑤直线AB与直线BC;
⑥直线AB与平面AC;
⑦平面A1B与平面AC.
解析:①点P∈直线AB;②点C 直线AB;
③点M∈平面AC;④点A1 平面AC;
⑤直线AB∩直线BC=点B;⑥直线AB 平面AC;
⑦平面A1B∩平面AC=直线AB.
(2)若点A在平面α内,直线a在平面α内,点A不在直线a上,用符号语言可表示为( )
A.A∈α,a α,A a
B.A∈α,a∈α,A a
C.A α,a α,A a
D.A∈α,a α,A a
答案:A
解析:点与线、面的关系用∈、 ;线与面的关系用 、 .B项中,“a∈α”错;C项中“A α”错;D项中“A a”错.
题型2 点、线共面问题
例2 (1)已知四条直线两两相交,且不共点,求证:这四条直线在同一平面内;
【解析】 已知:a,b,c,d四条直线两两相交,且不共点,求证:a,b,c,d四线共面.
证明:①若a,b,c三线共点于O,如图所示,∵O d,
∴经过d与点O有且只有一个平面α.
∵A,B,C分别是d与a,b,c的交点,
∴A,B,C三点在平面α内.
由公理1知a,b,c都在平面α内,
故a,b,c,d共面.
②若a,b,c,d无三线共点,如图所示,
∵a=A,
∴经过a,b有且仅有一个平面α,
∴B,C∈α.由公理1知c α.
同理,d α,从而有a,b,c,d共面.
综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.
(2)空间两两相交的三条直线,可以确定的平面数是( )
A.1 B.2
C.3 D.1或3
答案:D
解析:若三条直线两两相交共有三个交点,则确定1个平面;若三条直线两两相交且交于同一点时,若三条直线共面,则能确定1个平面,若三条直线不共面,则能确定3个平面.
状元随笔 四条直线两两相交且不共点,可能有两种情况:一是有三条直线共点;二是任意三条直线都不共点,故要分两种情况.
方法归纳
证明点线共面常用的方法
(1)纳入法:先由部分直线确定一个平面,再证明其他直线也在这个平面内.
(2)重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.
跟踪训练2 (1)一条直线与三条平行直线都相交,求证:这四条直线共面.
(2)如图所示,在正方体ABCD - A1B1C1D1中.
①AA1与CC1是否在同一平面内?
②点B,C1,D是否在同一平面内?
③画出平面ACC1A1与平面BC1D及平面ACD1与平面BDC1的交线.
解析:(1)已知:a∥b∥c,l=A,l=B,l=C.
求证:直线a,b,c,l共面.
证明:证法一:∵a∥b,∴a,b确定一个平面α,
∵l=A,l=B,∴A∈α,B∈α,故l α.
又∵a∥c,∴a,c确定一个平面β.
同理可证l β,∴α=a且α=l.
∵过两条相交直线a、l有且只有一个平面,
故α与β重合,即直线a,b,c,l共面.
证法二:由证法一得a、b、l共面α,也就是说b在a、l确定的平面α内.
同理可证c在a、l确定的平面α内.
∵过a和l只能确定一个平面,∴a,b,c,l共面.
(2)①在正方体ABCD - A1B1C1D1中,
因为AA1∥CC1,所以AA1与CC1可确定平面AC1,
所以AA1与CC1在同一平面内.
②因为点B,C1,D不共线,所以点B,C1,D可确定平面BC1D,所以点B,C1,D在同一平面内.
③如图,因为AC=O,D1C=E,
所以O∈平面AC1,O∈平面BC1D.
又C1∈平面AC1,C1∈平面BC1D.
所以平面AC1∩平面BC1D=OC1.
同理平面ACD1∩平面BDC1=OE.
题型3 点共线与线共点问题
【思考探究】 1.如图,在正方体ABCD - A1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面内?
[提示] 如图,连接BD1,
∵A1C∩平面ABC1D1=E,
∴E∈A1C,E∈平面ABC1D1.
∵A1C 平面A1BCD1,
∴E∈平面A1BCD1.
2.上述问题中,你能证明B,E,D1三点共线吗?
[提示] 由于平面A1BCD1与平面ABC1D1交于直线BD1,又E∈BD1,根据公理3可知B,E,D1三点共线.
例3 在正方体ABCD - A1B1C1D1中,E,F分别是AA1,AB的中点.
(1)证明:点E,F,C,D1共面;
(2)证明:D1E,DA,CF三线交于一点.
【证明】 (1)连接A1B,根据正方体的几何性质可知A1B∥CD1.由于E,F分别是AA1,AB的中点,所以EF∥A1B,
所以EF∥CD1,所以E,F,C,D1四点共面.
(2)由于EF∥CD1,EF≠CD1,所以D1E与CF延长后必相交,设交点为P,由于P∈D1E,D1E 平面ADD1A1,P∈CF,CF 平面ABCD,根据基本事实3可知P在平面ADD1A1与平面ABCD的交线DA上,所以D1E,DA,CF三线交于一点.
方法归纳
点共线与线共点的证明方法
(1)点共线:证明多点共线通常利用公理3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上,也可选择其中两点确定一条直线,然后证明其他点也在其上.
(2)三线共点:证明三线共点问题可把其中一条直线作为分别过其余两条直线的两个平面的交线,然后再证两条直线的交点在此直线上,此外还可先将其中一条直线看作某两个平面的交线,证明该交线与另两条直线分别交于两点,再证点重合,从而得三线共点.
跟踪训练3
在空间四边形ABCD中,H,G分别是AD,CD的中点,E,F分别为边AB,BC上的点,且==.
求证:(1)点E,F,G,H四点共面;
(2)直线EH,BD,FG相交于同一点.
证明:(1)如图所示,连接EF,HG,在空间四边形ABCD中,H,G分别是AD,CD的中点,
所以HG∥AC且HG=AC.
又==,所以EF∥AC且EF=AC.
故EF∥HG,即E,F,G,H四点共面.
(2)由(1)知EF∥HG且EF≠HG,
所以设EH与FG交于点P,因为EH 平面ABD,所以P在平面ABD内,同理P在平面BCD内,且平面ABD∩平面BCD=BD,
所以点P在直线BD上,
所以直线EH,BD,FG相交于一点.
题型4 由平面的基本性质做截面图形
例4 如图所示,G是正方体ABCD - A1B1C1D1的棱DD1延长线上的一点,E,F是棱AB,BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC;
(2)过三点E,F,D1.
【解析】 (1)连接GA交A1D1于点M,连接GC交C1D1于点N,从而可以得到过点G及AC的平面.
画法:连接GA交A1D1于点M,连接GC交C1D1于点N;
连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.
(2)根据两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,即可作出交线.
画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;
连接D1P交CC1于点M,连接D1Q交AA1于点N;
连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.
方法归纳
解决几何体的截面问题的基本方法
(1)直接法
用直接法解决截面问题的关键是:截面上的点在几何体的棱上,且两两在一个平面内,我们可以借助于基本事实2:如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内,直接解决这类问题.
(2)延长线法
用延长线法解决截面问题的关键是:截面上的点中至少有两个点在一个几何体的一个表面上,我们可以借助于基本事实2,如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内.直接解决这类问题.
跟踪训练4 (1)如图,在正方体ABCD - A1B1C1D1中,试画出平面AB1D1与平面ACC1A1的交线.
解析:记B1D1与A1C1的交点为O,连接AO,则AO即为平面AB1D1与平面ACC1A1的交线,如图:
(2)如图,直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABCD所在平面外一点,画出平面SBD和平面SAC的交线.
解析:延长BD和AC交于点O,连接SO,SO即为平面SBD和平面SAC的交线,如图:
