数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系 课件(共23张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.3.1空间直角坐标系 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 952.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
笛卡儿
(1596—1650)
法国著名哲学家,数学家,
解析几何的奠基人之一
-----恩格思评价:数学中的转
折点是笛卡儿的变数,有了变数,
运动进入了数学,有了变数,辨
证法进入了数学
数学史
x
O
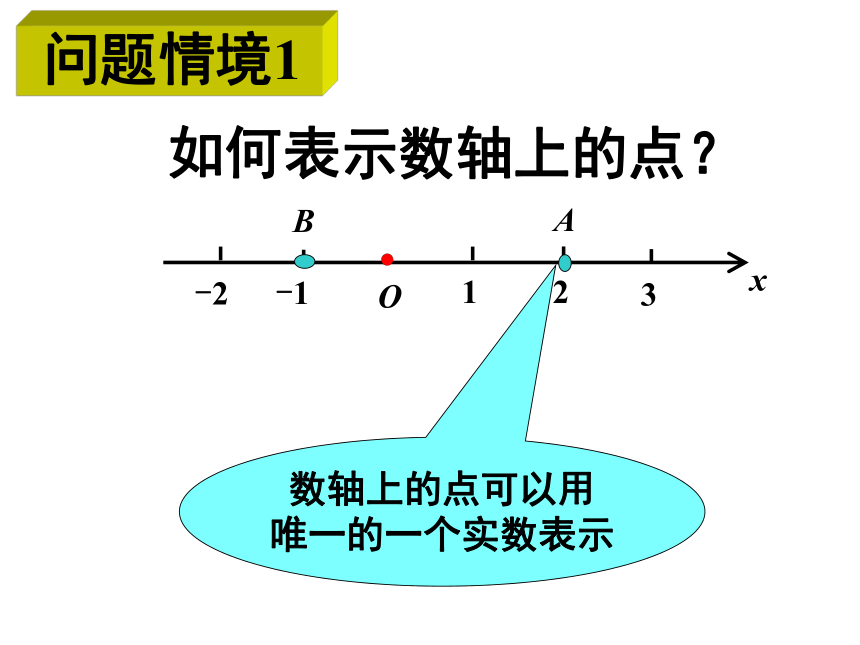
数轴上的点可以用
唯一的一个实数表示
-1
-2
1
2
3
A
B
如何表示数轴上的点?
问题情境1
平面中的点可以用有序实数对(x,y)来表示点
x
y
P
O
x
y
(x,y)
如何表示平面中的点?
问题情境2
y
O
x
z
猜想:如何确定教室里某位同学的头所在的位置?
创设情境,导入新课
江西大余中学 廖达凡
2009年05月20日
空间直角坐标系
课题
横轴
纵轴
竖轴
右手系
X
Y
Z
空间直角坐标系
右手螺旋法则:伸出右手,让四指与大拇指垂直,并使四指先指向x轴正方向,然后让四指沿握拳方向旋转90度指向y轴正方向,此时大拇指的指向即为z轴正向
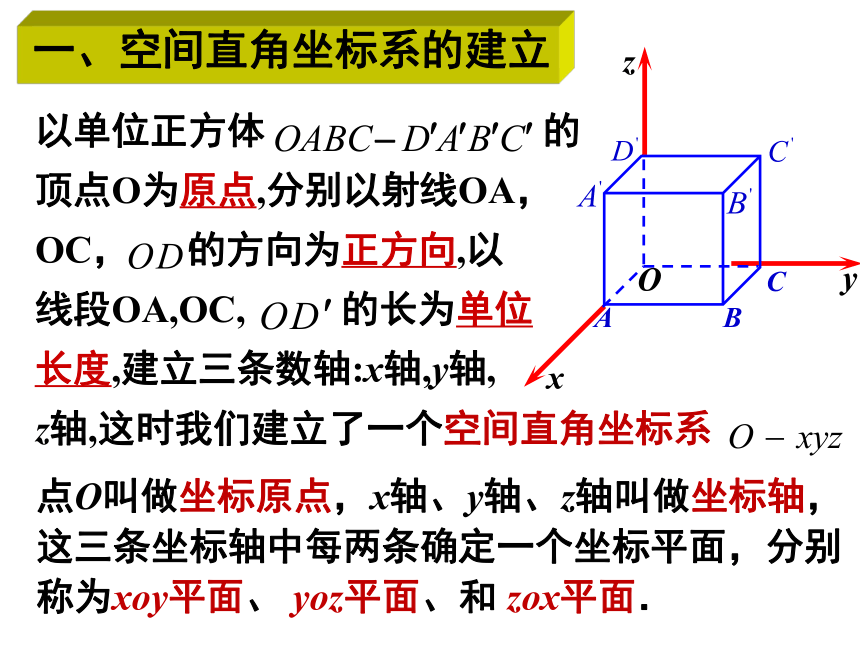
以单位正方体 的
顶点O为原点,分别以射线OA,
OC, 的方向为正方向,以
线段OA,OC, 的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系
y
x
z
A
B
C
O
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、 yoz平面、和 zox平面.
一、空间直角坐标系的建立
Ⅱ
Ⅶ
Ⅴ
Ⅵ
Ⅰ
Ⅲ
Ⅳ
Ⅷ
O
空间直角坐标系共有八个卦限
面
面
面
思考:在空间直角坐标系Oxyz中,三个坐标平面的位置关系如何?它们将空间分成几个部分?
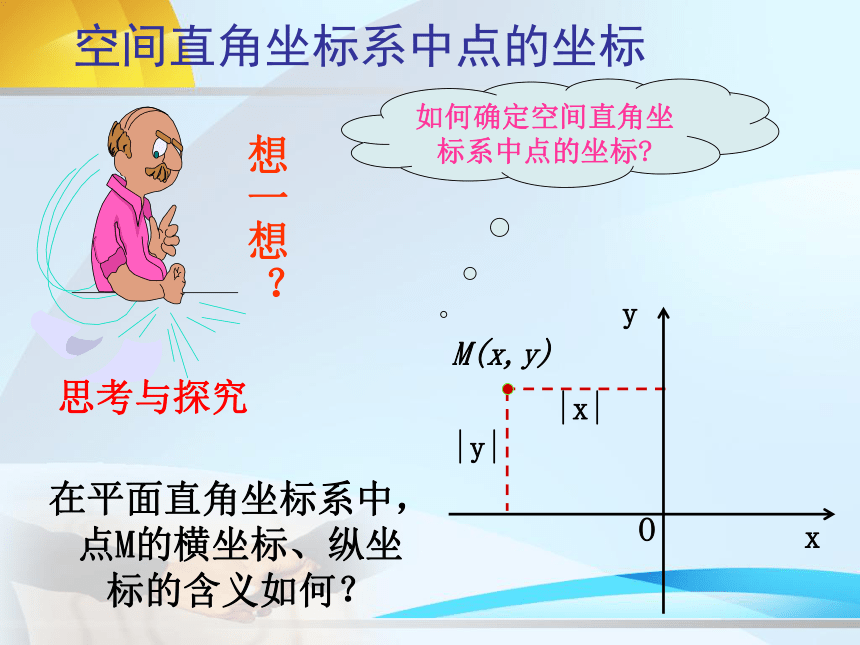
空间直角坐标系中点的坐标
想一想?
如何确定空间直角坐标系中点的坐标
|x|
|y|
O
x
M(x,y)
y
在平面直角坐标系中,点M的横坐标、纵坐标的含义如何?
思考与探究
x称为点P的横坐标
O
x
y
z
Px
Pz
x
z
y
P
Py
y称为点P的纵坐标
z称为点P的竖坐标
反之:
(x,y,z)对应唯一的点P
空间的点P
有序数组
三、空间中点的坐标
垂面法
反过来,对于一个有序实数组(x,y,z),它也唯一的对应着空间直角坐标系中的点。在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q, R分别过P、Q 、 R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
y
x
z
N
O
M
R
Q
P
空间直角坐标系中点的坐标
空间直角坐标系中点的坐标
M
M
N
N
Q
P
如图,M与z正半轴在xOy平面的同侧,那么点M的z坐标是线段MN的长度
如果M与z正半轴在xOy平面的异侧,那么点M的z坐标是线段MN的长度的相反数
M(x,y,0)
垂线法
(x,y,0)
(x,y,z)
抽象与概括
在空间直角坐标系中,对于空间任意一点P,都可以用一个三元有序数组(x,y ,z)来表示;反之,任何一个三元有序数组都可以确定空间中的一个点。这样,在空间直角坐标系中,点与三元有序数组之间建立了一一对应的关系。
空间直角坐标系中点的坐标
y
x
z
A
B
C
O
四棱柱 是单位正方体.如图建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标。
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
跟踪训练
规律:不见的那个就为“0”
O
x
y
z
1
1
1
A
D
C
B
E
F
点P的位置 原点O x轴上A y轴上B z轴上C
坐标形式
点P的位置 xOy面内D yOz面内E zOx面内F
坐标形式
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
四、特殊位置的点的坐标:
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
(1)坐标平面内的点:
(2)坐标轴上的点:
O
x
y
z
1
1
1
A
D
C
B
E
F
规律总结:
规律:不见的那个就为“0”
应用举例
x
y
O
x0
y0
(x0,y0)
P
(x0 , -y0)
P1
横坐标不变,
纵坐标相反。
(-x0 ,y0)
P2
横坐标相反,
纵坐标不变。
P3
横坐标相反,
纵坐标相反。
-y0
-x0
(-x0 , -y0)
关于谁对称谁不变
五、空间点的对称问题
类比探究1:
类比探究2:
点M(x,y,z)是空间直角坐标系O-xyz中的一点
(5)与点M关于平面xOy的对称点:
(x,y,-z)
(-x,y,z)
(x,-y,z)
(6)与点M关于平面yOz的对称点:
(7)与点M关于平面zOx的对称点:
五、空间点的对称问题
规律:见到谁谁不变,见不到变为相反数
1、空间直角坐标系的建立(三步)
2、空间直角坐标系的划分(八个卦限)
3、空间中点的坐标(一一对应)
4、特殊位置的点的坐标(表格)
5、空间点的对称问题
思想方法:数形结合、类比、化归
课堂小结:
x
y
z
o
路漫漫,其修远兮,吾将上下而求索
谢谢!
笛卡儿
(1596—1650)
法国著名哲学家,数学家,
解析几何的奠基人之一
-----恩格思评价:数学中的转
折点是笛卡儿的变数,有了变数,
运动进入了数学,有了变数,辨
证法进入了数学
数学史
x
O
数轴上的点可以用
唯一的一个实数表示
-1
-2
1
2
3
A
B
如何表示数轴上的点?
问题情境1
平面中的点可以用有序实数对(x,y)来表示点
x
y
P
O
x
y
(x,y)
如何表示平面中的点?
问题情境2
y
O
x
z
猜想:如何确定教室里某位同学的头所在的位置?
创设情境,导入新课
江西大余中学 廖达凡
2009年05月20日
空间直角坐标系
课题
横轴
纵轴
竖轴
右手系
X
Y
Z
空间直角坐标系
右手螺旋法则:伸出右手,让四指与大拇指垂直,并使四指先指向x轴正方向,然后让四指沿握拳方向旋转90度指向y轴正方向,此时大拇指的指向即为z轴正向
以单位正方体 的
顶点O为原点,分别以射线OA,
OC, 的方向为正方向,以
线段OA,OC, 的长为单位
长度,建立三条数轴:x轴,y轴,
z轴,这时我们建立了一个空间直角坐标系
y
x
z
A
B
C
O
点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xoy平面、 yoz平面、和 zox平面.
一、空间直角坐标系的建立
Ⅱ
Ⅶ
Ⅴ
Ⅵ
Ⅰ
Ⅲ
Ⅳ
Ⅷ
O
空间直角坐标系共有八个卦限
面
面
面
思考:在空间直角坐标系Oxyz中,三个坐标平面的位置关系如何?它们将空间分成几个部分?
空间直角坐标系中点的坐标
想一想?
如何确定空间直角坐标系中点的坐标
|x|
|y|
O
x
M(x,y)
y
在平面直角坐标系中,点M的横坐标、纵坐标的含义如何?
思考与探究
x称为点P的横坐标
O
x
y
z
Px
Pz
x
z
y
P
Py
y称为点P的纵坐标
z称为点P的竖坐标
反之:
(x,y,z)对应唯一的点P
空间的点P
有序数组
三、空间中点的坐标
垂面法
反过来,对于一个有序实数组(x,y,z),它也唯一的对应着空间直角坐标系中的点。在x 轴、y 轴和z 轴上依次取坐标为x,y和z的点P、Q, R分别过P、Q 、 R各作一个平面,分别垂直于x 轴、y 轴和z 轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.
y
x
z
N
O
M
R
Q
P
空间直角坐标系中点的坐标
空间直角坐标系中点的坐标
M
M
N
N
Q
P
如图,M与z正半轴在xOy平面的同侧,那么点M的z坐标是线段MN的长度
如果M与z正半轴在xOy平面的异侧,那么点M的z坐标是线段MN的长度的相反数
M(x,y,0)
垂线法
(x,y,0)
(x,y,z)
抽象与概括
在空间直角坐标系中,对于空间任意一点P,都可以用一个三元有序数组(x,y ,z)来表示;反之,任何一个三元有序数组都可以确定空间中的一个点。这样,在空间直角坐标系中,点与三元有序数组之间建立了一一对应的关系。
空间直角坐标系中点的坐标
y
x
z
A
B
C
O
四棱柱 是单位正方体.如图建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标。
(0,0,0)
(1,0,0)
(1,1,0)
(0,1,0)
(1,0,1)
(1,1,1)
(0,1,1)
(0,0,1)
跟踪训练
规律:不见的那个就为“0”
O
x
y
z
1
1
1
A
D
C
B
E
F
点P的位置 原点O x轴上A y轴上B z轴上C
坐标形式
点P的位置 xOy面内D yOz面内E zOx面内F
坐标形式
(0,0,0)
(x,0,0)
(0,y,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
四、特殊位置的点的坐标:
xoy平面上的点竖坐标为0
yoz平面上的点横坐标为0
xoz平面上的点纵坐标为0
x轴上的点纵坐标和竖坐标都为0
z轴上的点横坐标和纵坐标都为0
y轴上的点横坐标和竖坐标都为0
(1)坐标平面内的点:
(2)坐标轴上的点:
O
x
y
z
1
1
1
A
D
C
B
E
F
规律总结:
规律:不见的那个就为“0”
应用举例
x
y
O
x0
y0
(x0,y0)
P
(x0 , -y0)
P1
横坐标不变,
纵坐标相反。
(-x0 ,y0)
P2
横坐标相反,
纵坐标不变。
P3
横坐标相反,
纵坐标相反。
-y0
-x0
(-x0 , -y0)
关于谁对称谁不变
五、空间点的对称问题
类比探究1:
类比探究2:
点M(x,y,z)是空间直角坐标系O-xyz中的一点
(5)与点M关于平面xOy的对称点:
(x,y,-z)
(-x,y,z)
(x,-y,z)
(6)与点M关于平面yOz的对称点:
(7)与点M关于平面zOx的对称点:
五、空间点的对称问题
规律:见到谁谁不变,见不到变为相反数
1、空间直角坐标系的建立(三步)
2、空间直角坐标系的划分(八个卦限)
3、空间中点的坐标(一一对应)
4、特殊位置的点的坐标(表格)
5、空间点的对称问题
思想方法:数形结合、类比、化归
课堂小结:
x
y
z
o
路漫漫,其修远兮,吾将上下而求索
谢谢!
