数学人教A版(2019)选择性必修第一册2.2.1直线的点斜式方程 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.2.1直线的点斜式方程 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 965.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 23:40:28 | ||
图片预览


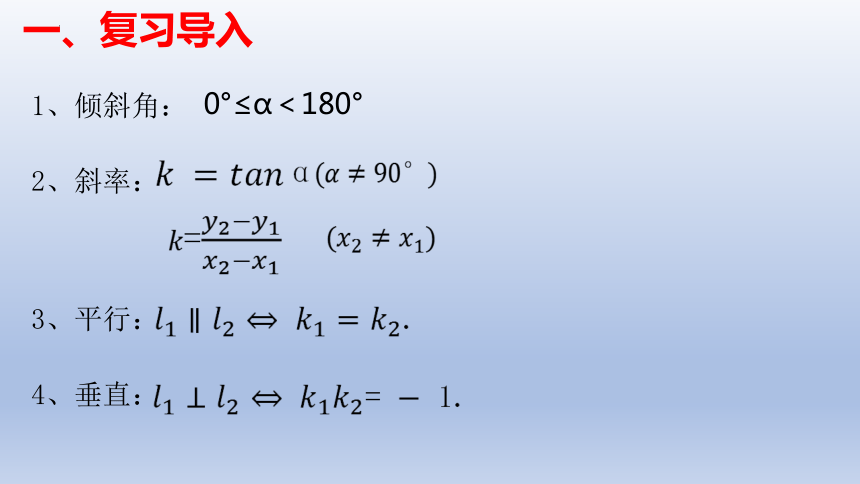



文档简介
(共15张PPT)
2.2.1
直线的点斜式方程
人教A版(2019)选择性必修第一册
学习目标
1. 能根据确定直线位置的几何要素,探索并掌握直线的点斜式与斜截式方程。
2. 会求直线的点斜式方程和斜截式方程。
3.能利用直线的点斜式方程、斜截式方程解决相应的问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
1、倾斜角:
0°≤α<180°
2、斜率:
α
=
3、平行:
.
4、垂直:
= 1.
二、新课讲授
1、直线的点斜式方程
问题1:给定一点和一个方向就可以确定一条直线,那么直线上的任意一点(x,y)与给定一点及斜率之间存在什么样的关系呢?
P
如图,设P (x,y)是直线上不同于点的任意点,
因为直线的斜率为,由斜率公式得
=
整理得 = ()
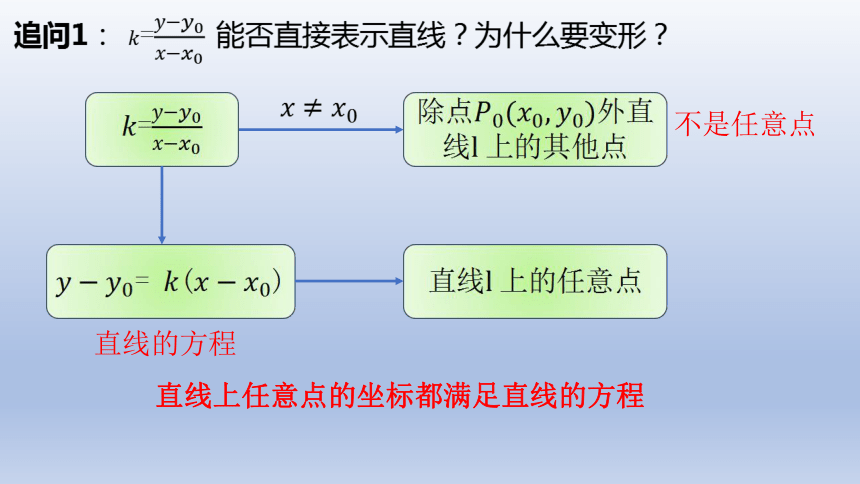
追问1: =能否直接表示直线?为什么要变形?
=
除外直线上的其他点
不是任意点
= ()
直线上的任意点
直线上任意点的坐标都满足直线的方程
直线的方程
追问2: 满足= ()的每个点是否都在直线上?
若点的坐标满足关系式= () ,
当= 时, ,
这时点与重合,点在直线上;
当≠ 时, 有=,
这时过点的直线的斜率为;
因为直线的斜率都为,且都过点,所以它们重合.
所以点在直线上.
所以,坐标满足方程的点都在直线上.
方程= ()称为过点,斜率为的直线点斜式方程,简称点斜式.
追问3: 直线经过点,且倾斜角为0°时,直线的方程是什么?
解法1:已知倾斜角为0°,得直线斜率0
代入直线的点斜式方程,得=0;
解法2:已知倾斜角为0°,得直线斜率0
这时直线与x轴平行或重合,方程为
追问4: 直线经过点,且倾斜角为90°时,直线的方程是什么?
解:当倾斜角为90°时,此时无意义,直线无斜率,
方程不能有点斜式表示;
这时直线与y轴平行或重合,
直线上的每一点的横坐标都等于,
即它的方程为 ,
小结:
直线
斜率存在
斜率不存在
倾斜角为0°,直线方程为=0
倾斜角不为0°,直线方程为
= ()
= ()
倾斜角为90°,无点斜式方程
2、直线的斜截式方程
例1 直线经过点(2,3),且倾斜角α=45°,求直线的点斜式方程,并画出直线.
解:直线经过点(2,3),且倾斜角α=45°
则直线斜率= =1,代入点斜式方程= ()
得: = [)],
即= .
取直线(),
取-1,代入直线方程,得=
则直线由(2,3)与(1,4)确定,作图如有所示.
问题2:如何斜率为的直线方程呢?
直线
斜截式方程
斜:直线的斜率
截:直线在y轴上的截距,即直线与y轴交点的纵坐标
注:①截距不是距离;
②截距正可负可为零
斜截式是特殊的点斜式,两者都只能表示斜率存在的直线.
问题3:如何直线方程角度认识一次函数呢?
3、直线与函数
直线上任意点的坐标(x,y)满足的代数关系
直线方程
变量x,y之间的对应关系
一次函数
一次函数的图象是直线
:直线的斜率
:直线在y轴上的截距
问题1:一次函数3, 对应的图象都是直线,着三条直线的斜率和直线在y轴上的截距是什么?
一次函数 直线斜率 直线在y轴上的截距 直线与y轴的交点
3
2
-1
(0,-1)
-1
3
(0,3)
3
0
(0,0)
三、巩固新知
例2 已知直线: ,试讨论:
(1) 的条件是什么?
(2) 的条件是什么?
解:(1)若,则= ,又与y轴的交点不同,即
反之= , 则.
(2)若,则 =-1,
反之, 则.
四、课堂小结
1、直线点斜式方程:= ()
2、直线斜截式方程:
3、直线方程与一次函数的关系
五、作业布置
课本P62:练习 第3、4题
2.2.1
直线的点斜式方程
人教A版(2019)选择性必修第一册
学习目标
1. 能根据确定直线位置的几何要素,探索并掌握直线的点斜式与斜截式方程。
2. 会求直线的点斜式方程和斜截式方程。
3.能利用直线的点斜式方程、斜截式方程解决相应的问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
1、倾斜角:
0°≤α<180°
2、斜率:
α
=
3、平行:
.
4、垂直:
= 1.
二、新课讲授
1、直线的点斜式方程
问题1:给定一点和一个方向就可以确定一条直线,那么直线上的任意一点(x,y)与给定一点及斜率之间存在什么样的关系呢?
P
如图,设P (x,y)是直线上不同于点的任意点,
因为直线的斜率为,由斜率公式得
=
整理得 = ()
追问1: =能否直接表示直线?为什么要变形?
=
除外直线上的其他点
不是任意点
= ()
直线上的任意点
直线上任意点的坐标都满足直线的方程
直线的方程
追问2: 满足= ()的每个点是否都在直线上?
若点的坐标满足关系式= () ,
当= 时, ,
这时点与重合,点在直线上;
当≠ 时, 有=,
这时过点的直线的斜率为;
因为直线的斜率都为,且都过点,所以它们重合.
所以点在直线上.
所以,坐标满足方程的点都在直线上.
方程= ()称为过点,斜率为的直线点斜式方程,简称点斜式.
追问3: 直线经过点,且倾斜角为0°时,直线的方程是什么?
解法1:已知倾斜角为0°,得直线斜率0
代入直线的点斜式方程,得=0;
解法2:已知倾斜角为0°,得直线斜率0
这时直线与x轴平行或重合,方程为
追问4: 直线经过点,且倾斜角为90°时,直线的方程是什么?
解:当倾斜角为90°时,此时无意义,直线无斜率,
方程不能有点斜式表示;
这时直线与y轴平行或重合,
直线上的每一点的横坐标都等于,
即它的方程为 ,
小结:
直线
斜率存在
斜率不存在
倾斜角为0°,直线方程为=0
倾斜角不为0°,直线方程为
= ()
= ()
倾斜角为90°,无点斜式方程
2、直线的斜截式方程
例1 直线经过点(2,3),且倾斜角α=45°,求直线的点斜式方程,并画出直线.
解:直线经过点(2,3),且倾斜角α=45°
则直线斜率= =1,代入点斜式方程= ()
得: = [)],
即= .
取直线(),
取-1,代入直线方程,得=
则直线由(2,3)与(1,4)确定,作图如有所示.
问题2:如何斜率为的直线方程呢?
直线
斜截式方程
斜:直线的斜率
截:直线在y轴上的截距,即直线与y轴交点的纵坐标
注:①截距不是距离;
②截距正可负可为零
斜截式是特殊的点斜式,两者都只能表示斜率存在的直线.
问题3:如何直线方程角度认识一次函数呢?
3、直线与函数
直线上任意点的坐标(x,y)满足的代数关系
直线方程
变量x,y之间的对应关系
一次函数
一次函数的图象是直线
:直线的斜率
:直线在y轴上的截距
问题1:一次函数3, 对应的图象都是直线,着三条直线的斜率和直线在y轴上的截距是什么?
一次函数 直线斜率 直线在y轴上的截距 直线与y轴的交点
3
2
-1
(0,-1)
-1
3
(0,3)
3
0
(0,0)
三、巩固新知
例2 已知直线: ,试讨论:
(1) 的条件是什么?
(2) 的条件是什么?
解:(1)若,则= ,又与y轴的交点不同,即
反之= , 则.
(2)若,则 =-1,
反之, 则.
四、课堂小结
1、直线点斜式方程:= ()
2、直线斜截式方程:
3、直线方程与一次函数的关系
五、作业布置
课本P62:练习 第3、4题
