第五单元圆的面积—外圆内方和外方内圆(课件)(共18张PPT)-六年级上册数学人教版
文档属性
| 名称 | 第五单元圆的面积—外圆内方和外方内圆(课件)(共18张PPT)-六年级上册数学人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 17:55:35 | ||
图片预览




文档简介
(共18张PPT)
第五章 圆
外方内圆和外圆内方
一、趣味导入
天圆地方
在中国古代,人们认为天是圆形的,像一把张开的大伞覆盖在地上,地是方形的。这一学说被称为“天圆地方”说。
二、探索新知
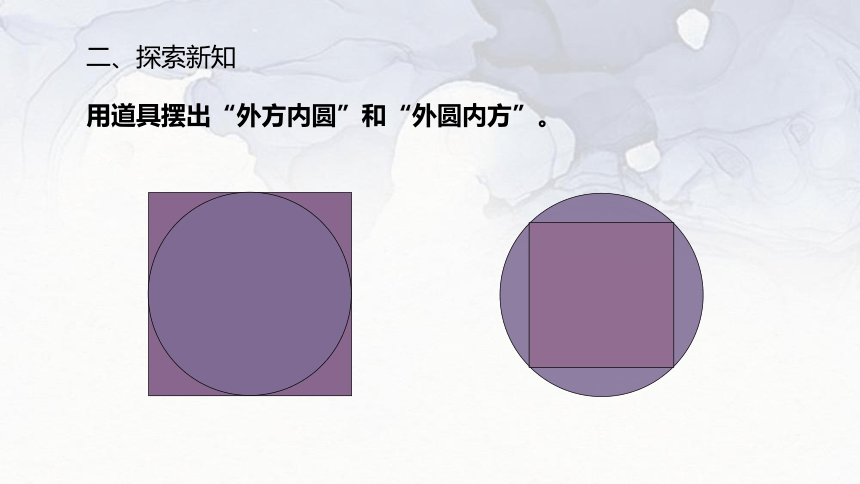
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
观察正方形的边长和圆的半径有什么关系呢?
二、探索新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
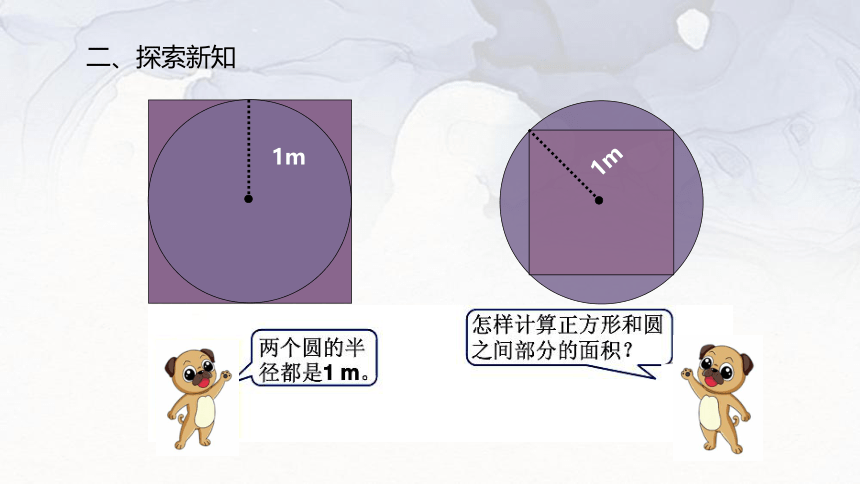
你能求出正方形和圆之间部分的面积吗?
二、探索新知
用道具摆出“外方内圆”和“外圆内方”。
二、探索新知
1m
1m
1m
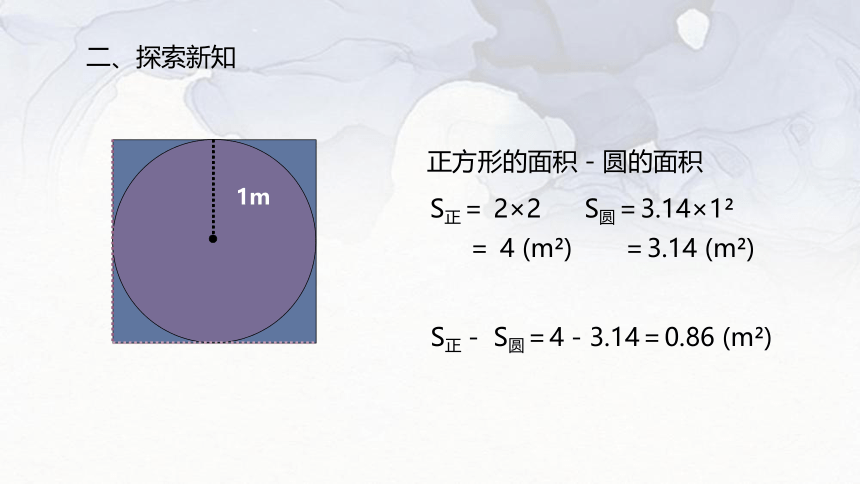
S正= 2×2
= 4 (m )
S正- S圆=4-3.14=0.86 (m )
S圆=3.14×1
=3.14 (m )
正方形的面积-圆的面积
二、探索新知
二、探索新知
圆的面积-正方形的面积
S正=(2×1÷2) ×2
= 2(m )
S圆=3.14×1
=3.14(m )
S圆-S正=3.14-2=1.14 (m )
1m
底=直径=2m
高=半径=
二、探索新知
圆的面积-正方形的面积
S正=(1×1÷2) ×4
= 2(m )
S圆=3.14×1
=3.14(m )
S圆-S正=3.14-2=1.14 (m )
1m
底=半径=1m
高=半径=
二、探索新知
二、探索新知
假设圆的半径为r,则三个图形的面积分别可以表示为:
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
外方内圆之间部分的面积:
外圆内方之间部分的面积:
4r -πr =0.86r
πr -2r =1.14r
二、探索新知
假设圆的半径为r,则三个图形的面积分别可以表示为:
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
大正方形面积:圆的面积:小正方形面积 = 4 : π : 2
大正方形面积是小正方形面积的2倍!
三、课堂练习
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。 外面的圆与内部的正方形之间的面积是多少?
S正= S三×2
=24×(24÷2)÷2×2
=288 (m )
S圆= πr 2
=3.14×(24÷2)
=452.16 (m )
S圆- S正=452.16-288=164.16 (m )
四、思考
如何在一个正方形内画一个最大的圆?
如何在一个圆内画一个最大的正方形?
四、思考
如何在一个正方形内画一个最大的圆?
1.先在纸上画一个正方形;
2.连接正方形的两条对角线,两条对角线的交点是圆的中心;
3.画一个直径为正方形边长的圆。
此圆形是正方形中最大的圆。
四、思考
如何在一个圆内画一个最大的正方形?
1.先在纸上确定圆心,然后确定半径的长度,最后用圆规画一个圆;
2.根据圆心的位置,画出圆的一条直径,只要经过圆心即可轻松画出直径;
3.再画出垂直于这条直径的另一条直径;
4.画完后,两条直径在圆上会出现4个交点;
5.用尺子连接这4个交点,即可画一个最大的正方形。
五、课堂小结
谢谢观看
单击此处添加副标题
第五章 圆
外方内圆和外圆内方
一、趣味导入
天圆地方
在中国古代,人们认为天是圆形的,像一把张开的大伞覆盖在地上,地是方形的。这一学说被称为“天圆地方”说。
二、探索新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
观察正方形的边长和圆的半径有什么关系呢?
二、探索新知
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。
你能求出正方形和圆之间部分的面积吗?
二、探索新知
用道具摆出“外方内圆”和“外圆内方”。
二、探索新知
1m
1m
1m
S正= 2×2
= 4 (m )
S正- S圆=4-3.14=0.86 (m )
S圆=3.14×1
=3.14 (m )
正方形的面积-圆的面积
二、探索新知
二、探索新知
圆的面积-正方形的面积
S正=(2×1÷2) ×2
= 2(m )
S圆=3.14×1
=3.14(m )
S圆-S正=3.14-2=1.14 (m )
1m
底=直径=2m
高=半径=
二、探索新知
圆的面积-正方形的面积
S正=(1×1÷2) ×4
= 2(m )
S圆=3.14×1
=3.14(m )
S圆-S正=3.14-2=1.14 (m )
1m
底=半径=1m
高=半径=
二、探索新知
二、探索新知
假设圆的半径为r,则三个图形的面积分别可以表示为:
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
外方内圆之间部分的面积:
外圆内方之间部分的面积:
4r -πr =0.86r
πr -2r =1.14r
二、探索新知
假设圆的半径为r,则三个图形的面积分别可以表示为:
大正方形的面积:
圆 的面积:
小正方形的面积:
(2r) = 4r
πr
(2r×r÷2)×2 = 2r
大正方形面积:圆的面积:小正方形面积 = 4 : π : 2
大正方形面积是小正方形面积的2倍!
三、课堂练习
1.右图是一面我国唐代外圆内方的铜镜。铜镜的直径是24 cm。 外面的圆与内部的正方形之间的面积是多少?
S正= S三×2
=24×(24÷2)÷2×2
=288 (m )
S圆= πr 2
=3.14×(24÷2)
=452.16 (m )
S圆- S正=452.16-288=164.16 (m )
四、思考
如何在一个正方形内画一个最大的圆?
如何在一个圆内画一个最大的正方形?
四、思考
如何在一个正方形内画一个最大的圆?
1.先在纸上画一个正方形;
2.连接正方形的两条对角线,两条对角线的交点是圆的中心;
3.画一个直径为正方形边长的圆。
此圆形是正方形中最大的圆。
四、思考
如何在一个圆内画一个最大的正方形?
1.先在纸上确定圆心,然后确定半径的长度,最后用圆规画一个圆;
2.根据圆心的位置,画出圆的一条直径,只要经过圆心即可轻松画出直径;
3.再画出垂直于这条直径的另一条直径;
4.画完后,两条直径在圆上会出现4个交点;
5.用尺子连接这4个交点,即可画一个最大的正方形。
五、课堂小结
谢谢观看
单击此处添加副标题
