人教B版高中数学必修第二册 4.6 函数的应用(二) 课件(共39张PPT)
文档属性
| 名称 | 人教B版高中数学必修第二册 4.6 函数的应用(二) 课件(共39张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
4.6 函数的应用(二)
第四章 指数函数、对数函数与幂函数
1
15分钟对点练
PART ONE
知识点一 指数型函数模型
1.某个病毒经30分钟繁殖为原来的2倍,且知病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k=________,经过5小时,1个病毒能繁殖为________个.
答案 2ln 2 1024
解析
解
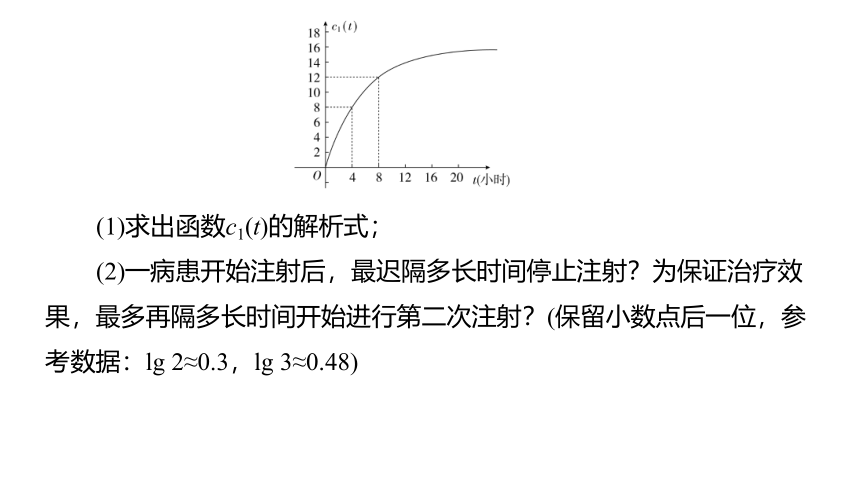
(1)求出函数c1(t)的解析式;
(2)一病患开始注射后,最迟隔多长时间停止注射?为保证治疗效果,最多再隔多长时间开始进行第二次注射?(保留小数点后一位,参考数据:lg 2≈0.3,lg 3≈0.48)
解
解
解
解
[名师点拨] 对数型函数模型:y=mlogax+c(m≠0,a>0且a≠1),对数型函数模型一般给出函数关系式,然后利用对数的运算求解.
知识点三 幂函数模型
6.某药厂研制出一种新型药剂,投放市场后其广告投入x(万元)与药品利润y(万元)存在的关系为y=xα(α为常数),其中x不超过5万元.已知去年投入广告费用为3万元时,药品利润为27万元,若今年广告费用投入5万元,预计今年药品利润为________万元.
答案 125
解析 由已知投入广告费用为3万元时,药品利润为27万元,代入y=xα中,即3α=27,解得α=3,故函数关系式为y=x3,所以当x=5时,y=125.
7.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式;
(2)假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的函数解析式;
(3)已知(2)中的气体通过的管道半径为5 cm,计算该气体的流量(精确到1 cm3/s).
解
2
30分钟综合练
PART TWO
一、选择题
1.某公司为适应市场需求,对产品结构进行了重大调整,调整后初期利润增长迅速,后期增长越来越慢.若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
解析 由题意分析,符合对数型函数的特点.
二、填空题
6.一个驾驶员喝了少量酒后,血液中的酒精含量迅速上升到0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时25%的速度减少,为了保障交通安全,规定驾驶员血液中的酒精含量不得超过0.09 mg/mL,那么这个驾驶员至少要经过________小时才能开车.(精确到1小时,参考数据:lg 2≈0.30,lg 3≈0.48)
答案 5
7.某食品的保鲜时间y(单位:小时)与储藏温度x(单位: ℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是________小时.
答案 24
三、解答题
9.国家正在大力倡导环保意识、生态意识,构建全社会共同参与的环境治理体系,让生态环保思想成为社会生活中的主流文化.某化工企业通过改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量r0=2 mg/m3,首次改良工艺后排放的废气中含有的污染物数量r1=1.94 mg/m3,第n次改良工艺后所排放的废气中的污染物数量rn满足函数关系rn=r0-(r0-r1)·50.5n+p(p∈R,n∈N+),其中n是指改良工艺的次数.
(1)求改良后所排放的废气中含有的污染物数量的函数关系式;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过0.08 mg/m3.求至少进行多少次改良工艺后才能使该企业所排放的废气中含有的污染物数量达标?(参考数据:lg 2≈0.3)
解 (1)由题意,得r0=2,r1=1.94,所以当n=1时,r1=r0-(r0-r1)·50.5+p,即1.94=2-(2-1.94)×50.5+p,解得p=-0.5,所以rn=2-0.06×50.5n-0.5(n∈N+),故改良后所排放的废气中含有的污染物数量的函数关系式为rn=2-0.06×50.5n-0.5(n∈N+).
解
解
解
解
本课结束
4.6 函数的应用(二)
第四章 指数函数、对数函数与幂函数
1
15分钟对点练
PART ONE
知识点一 指数型函数模型
1.某个病毒经30分钟繁殖为原来的2倍,且知病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k=________,经过5小时,1个病毒能繁殖为________个.
答案 2ln 2 1024
解析
解
(1)求出函数c1(t)的解析式;
(2)一病患开始注射后,最迟隔多长时间停止注射?为保证治疗效果,最多再隔多长时间开始进行第二次注射?(保留小数点后一位,参考数据:lg 2≈0.3,lg 3≈0.48)
解
解
解
解
[名师点拨] 对数型函数模型:y=mlogax+c(m≠0,a>0且a≠1),对数型函数模型一般给出函数关系式,然后利用对数的运算求解.
知识点三 幂函数模型
6.某药厂研制出一种新型药剂,投放市场后其广告投入x(万元)与药品利润y(万元)存在的关系为y=xα(α为常数),其中x不超过5万元.已知去年投入广告费用为3万元时,药品利润为27万元,若今年广告费用投入5万元,预计今年药品利润为________万元.
答案 125
解析 由已知投入广告费用为3万元时,药品利润为27万元,代入y=xα中,即3α=27,解得α=3,故函数关系式为y=x3,所以当x=5时,y=125.
7.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式;
(2)假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的函数解析式;
(3)已知(2)中的气体通过的管道半径为5 cm,计算该气体的流量(精确到1 cm3/s).
解
2
30分钟综合练
PART TWO
一、选择题
1.某公司为适应市场需求,对产品结构进行了重大调整,调整后初期利润增长迅速,后期增长越来越慢.若要建立恰当的函数模型来反映该公司调整后利润y与时间x的关系,可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
解析 由题意分析,符合对数型函数的特点.
二、填空题
6.一个驾驶员喝了少量酒后,血液中的酒精含量迅速上升到0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时25%的速度减少,为了保障交通安全,规定驾驶员血液中的酒精含量不得超过0.09 mg/mL,那么这个驾驶员至少要经过________小时才能开车.(精确到1小时,参考数据:lg 2≈0.30,lg 3≈0.48)
答案 5
7.某食品的保鲜时间y(单位:小时)与储藏温度x(单位: ℃)满足函数关系y=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是________小时.
答案 24
三、解答题
9.国家正在大力倡导环保意识、生态意识,构建全社会共同参与的环境治理体系,让生态环保思想成为社会生活中的主流文化.某化工企业通过改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量r0=2 mg/m3,首次改良工艺后排放的废气中含有的污染物数量r1=1.94 mg/m3,第n次改良工艺后所排放的废气中的污染物数量rn满足函数关系rn=r0-(r0-r1)·50.5n+p(p∈R,n∈N+),其中n是指改良工艺的次数.
(1)求改良后所排放的废气中含有的污染物数量的函数关系式;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过0.08 mg/m3.求至少进行多少次改良工艺后才能使该企业所排放的废气中含有的污染物数量达标?(参考数据:lg 2≈0.3)
解 (1)由题意,得r0=2,r1=1.94,所以当n=1时,r1=r0-(r0-r1)·50.5+p,即1.94=2-(2-1.94)×50.5+p,解得p=-0.5,所以rn=2-0.06×50.5n-0.5(n∈N+),故改良后所排放的废气中含有的污染物数量的函数关系式为rn=2-0.06×50.5n-0.5(n∈N+).
解
解
解
解
本课结束
