人教B版高中数学必修第二册 4.4 幂函数 同步练习(含解析)
文档属性
| 名称 | 人教B版高中数学必修第二册 4.4 幂函数 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 112.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览


文档简介
人教B版高中数学必修第二册 4.4 幂函数 同步练习
必备知识基础练 进阶训练第一层
1.下列函数是幂函数的是( )
A.y=5x B.y=x5
C.y=5x D.y=(x+1)3
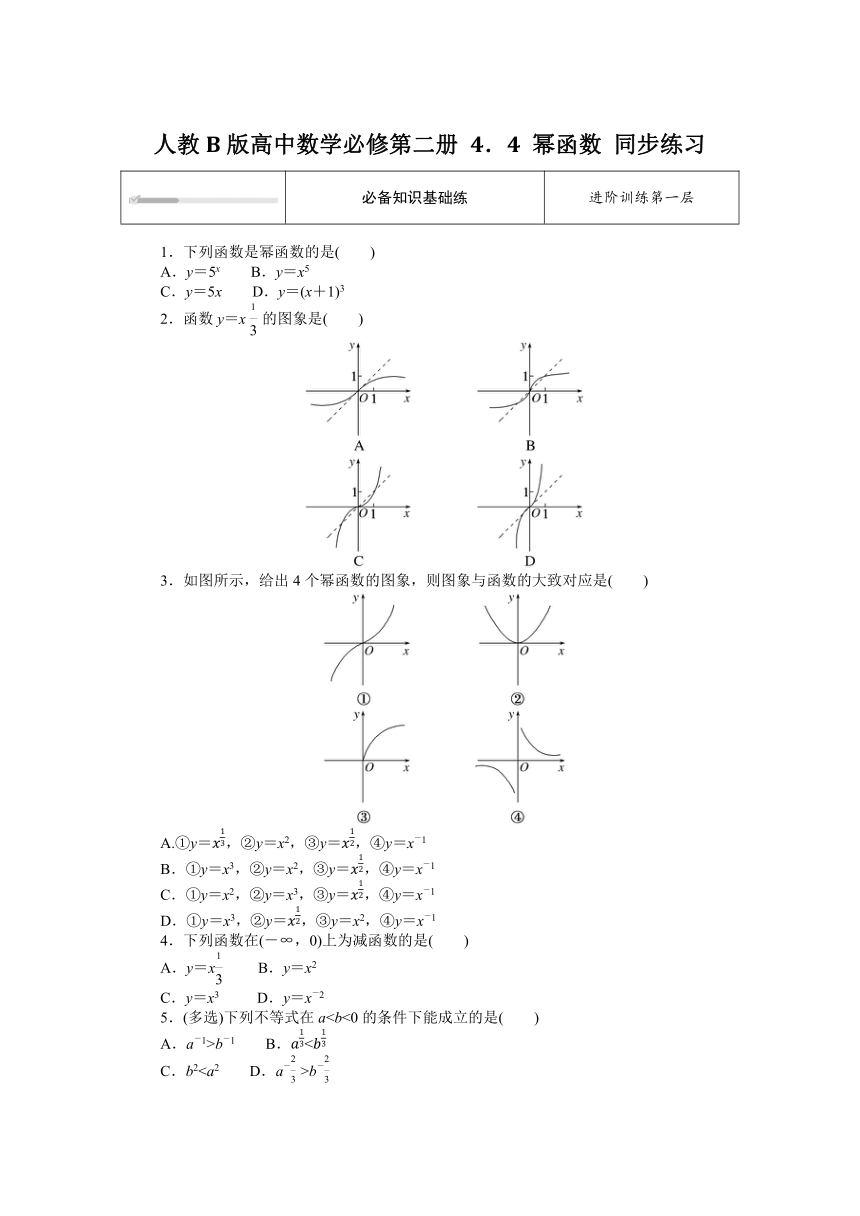
2.函数y=x的图象是( )
3.如图所示,给出4个幂函数的图象,则图象与函数的大致对应是( )
A.①y=,②y=x2,③y=,④y=x-1
B.①y=x3,②y=x2,③y=,④y=x-1
C.①y=x2,②y=x3,③y=,④y=x-1
D.①y=x3,②y=,③y=x2,④y=x-1
4.下列函数在(-∞,0)上为减函数的是( )
A.y=x B.y=x2
C.y=x3 D.y=x-2
5.(多选)下列不等式在aA.a-1>b-1 B.<
C.b2b-
6.设a=,b=,c=,则a,b,c的大小关系是( )
A.a<b<c B.b<a<c
C.c<a<b D.b<c<a
关键能力综合练 进阶训练第二层
7.(多选)如图所示,图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
8.若<,则a的取值范围是( )
A.(,) B.(,)
C.(,2) D.(,+∞)
9.(多选)定义域和值域相等的函数为“等域函数”,下列幂函数为“等域函数”的是( )
A.y=x3 B.y=x-
C.y= D.y=x2
10.,,从小到大依次是________.
11.若幂函数f(x)= (m∈Z)的图象与坐标轴无公共点,且关于原点对称,则实数m的取值集合为________.
12.已知幂函数y=f(x)=,其中m∈{x|-2(1)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(-x)+f(x)=0.
求同时满足(1)(2)的幂函数f(x)的解析式,并求x∈[0,3]时f(x)的值域.
核心素养升级练 进阶训练第三层
13.幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图象是一组美丽的曲线.设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA,那么,αβ等于________.
14.已知幂函数f(x)=(m2-5m+7)x-m-1(m∈R)为偶函数.
(1)则f()=________;
(2)若f(2a+1)=f(a),则实数a的值为________.
参考答案与解析
1.答案:B
解析:函数y=5x是指数函数,不是幂函数;函数y=5x是正比例函数,不是幂函数;函数y=(x+1)3的底数不是自变量x,不是幂函数;函数y=x5是幂函数.
2.答案:B
解析:∵当x>1时,x>x;当x=1时,x=x,所以A、C、D均不正确,选B.
3.答案:B
解析:因为y=x3的定义域为R且为奇函数,故应为图①;y=x2为开口向上的抛物线且顶点为原点,应为图②,同理可得出选项B正确.
4.答案:B
解析:∵A,C项在(-∞,0)上为增函数;D项中y=x-2=在(-∞,0)上也是增函数,故选B.
5.答案:ABC
解析:分别构造函数y=x-1,y=,y=x2,y=x-,其中函数y=x-1,y=x2在(-∞,0)上为减函数,故A、C成立,
而y=,y=x-为(-∞,0)上的增函数,从而B成立,D不成立.
6.答案:B
解析:由于函数y=()x在它的定义域R上是减函数,∴a=>b=>0.由于函数y=x在它的定义域R上是增函数,且>,故有c=>a=,故a,b,c的大小关系是b<a<c,故选B.
7.答案:B
解析:根据幂函数y=xn的性质,在第一象限内的图象当n>0时,n越大,y=xn递增速度越快,故C1的n=2,C2的n=;当n<0时,|n|越大,曲线越陡峭,所以曲线C3的n=-,曲线C4的n=-2,故选B.
8.答案:B
解析:令f(x)=x-=,∴f(x)的定义域是(0,+∞),且在(0,+∞)上是减函数,故原不等式等价于解得9.答案:ABC
解析:y=x3的定义域和值域都为R,A正确;y=x-的定义域和值域都为(-∞,0)∪(0,+∞),B正确;y=的定义域和值域都为[0,+∞),C正确;y=x2的定义域为R,值域为[0,+∞),D错误.
10.答案:0.25-<6.25<0.16-
解析:∵0.25-=0.5-<0.16-,0.25-=<6.25,6.25=2.5=0.4-<0.16-,∴0.25-<6.25<0.16-.
11.答案:{0,2}
解析:幂函数f(x)=xm2-2m-3(m∈Z)的图象与坐标轴无公共点,且关于原点对称,可得m2-2m-3<0(m∈Z),并且m2-2m-3为奇数,解得m=0,或m=2,则实数m的取值集合为{0,2}.
12.答案:f(x)=x3 [0,27]
解析:因为m∈{x|-2当m=-1时,f(x)=x2,只满足条件(1)而不满足条件(2);
当m=1时,f(x)=x0,条件(1)(2)都不满足;
当m=0时,f(x)=x3,条件(1)(2)都满足,且在区间[0,3]上是增函数,所以x∈[0,3]时,函数f(x)的值域为[0,27].
13.答案:1
解析:因为BM=MN=NA,点A(1,0),点B(0,1),
所以M(,),N(,),分别代入y=xα,y=xβ,
则α=log,β=log,
所以α·β=log·log=1.
14.答案:(1)16 (2)-1或-
解析:(1)由m2-5m+7=1,得m=2或3,
当m=2时,f(x)=x-3是奇函数,∴不满足题意,
∴m=2舍去;
当m=3时,f(x)=x-4,满足题意,
∴f(x)=x-4,
∴f()=()-4=16.
(2)由f(x)=x-4为偶函数和f(2a+1)=f(a)可得|2a+1|=|a|,即2a+1=a或2a+1=-a,解得a=-1或a=-.
必备知识基础练 进阶训练第一层
1.下列函数是幂函数的是( )
A.y=5x B.y=x5
C.y=5x D.y=(x+1)3
2.函数y=x的图象是( )
3.如图所示,给出4个幂函数的图象,则图象与函数的大致对应是( )
A.①y=,②y=x2,③y=,④y=x-1
B.①y=x3,②y=x2,③y=,④y=x-1
C.①y=x2,②y=x3,③y=,④y=x-1
D.①y=x3,②y=,③y=x2,④y=x-1
4.下列函数在(-∞,0)上为减函数的是( )
A.y=x B.y=x2
C.y=x3 D.y=x-2
5.(多选)下列不等式在a
C.b2
6.设a=,b=,c=,则a,b,c的大小关系是( )
A.a<b<c B.b<a<c
C.c<a<b D.b<c<a
关键能力综合练 进阶训练第二层
7.(多选)如图所示,图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
8.若<,则a的取值范围是( )
A.(,) B.(,)
C.(,2) D.(,+∞)
9.(多选)定义域和值域相等的函数为“等域函数”,下列幂函数为“等域函数”的是( )
A.y=x3 B.y=x-
C.y= D.y=x2
10.,,从小到大依次是________.
11.若幂函数f(x)= (m∈Z)的图象与坐标轴无公共点,且关于原点对称,则实数m的取值集合为________.
12.已知幂函数y=f(x)=,其中m∈{x|-2
(2)对任意的x∈R,都有f(-x)+f(x)=0.
求同时满足(1)(2)的幂函数f(x)的解析式,并求x∈[0,3]时f(x)的值域.
核心素养升级练 进阶训练第三层
13.幂函数y=xα,当α取不同的正数时,在区间[0,1]上它们的图象是一组美丽的曲线.设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA,那么,αβ等于________.
14.已知幂函数f(x)=(m2-5m+7)x-m-1(m∈R)为偶函数.
(1)则f()=________;
(2)若f(2a+1)=f(a),则实数a的值为________.
参考答案与解析
1.答案:B
解析:函数y=5x是指数函数,不是幂函数;函数y=5x是正比例函数,不是幂函数;函数y=(x+1)3的底数不是自变量x,不是幂函数;函数y=x5是幂函数.
2.答案:B
解析:∵当x>1时,x>x;当x=1时,x=x,所以A、C、D均不正确,选B.
3.答案:B
解析:因为y=x3的定义域为R且为奇函数,故应为图①;y=x2为开口向上的抛物线且顶点为原点,应为图②,同理可得出选项B正确.
4.答案:B
解析:∵A,C项在(-∞,0)上为增函数;D项中y=x-2=在(-∞,0)上也是增函数,故选B.
5.答案:ABC
解析:分别构造函数y=x-1,y=,y=x2,y=x-,其中函数y=x-1,y=x2在(-∞,0)上为减函数,故A、C成立,
而y=,y=x-为(-∞,0)上的增函数,从而B成立,D不成立.
6.答案:B
解析:由于函数y=()x在它的定义域R上是减函数,∴a=>b=>0.由于函数y=x在它的定义域R上是增函数,且>,故有c=>a=,故a,b,c的大小关系是b<a<c,故选B.
7.答案:B
解析:根据幂函数y=xn的性质,在第一象限内的图象当n>0时,n越大,y=xn递增速度越快,故C1的n=2,C2的n=;当n<0时,|n|越大,曲线越陡峭,所以曲线C3的n=-,曲线C4的n=-2,故选B.
8.答案:B
解析:令f(x)=x-=,∴f(x)的定义域是(0,+∞),且在(0,+∞)上是减函数,故原不等式等价于解得
解析:y=x3的定义域和值域都为R,A正确;y=x-的定义域和值域都为(-∞,0)∪(0,+∞),B正确;y=的定义域和值域都为[0,+∞),C正确;y=x2的定义域为R,值域为[0,+∞),D错误.
10.答案:0.25-<6.25<0.16-
解析:∵0.25-=0.5-<0.16-,0.25-=<6.25,6.25=2.5=0.4-<0.16-,∴0.25-<6.25<0.16-.
11.答案:{0,2}
解析:幂函数f(x)=xm2-2m-3(m∈Z)的图象与坐标轴无公共点,且关于原点对称,可得m2-2m-3<0(m∈Z),并且m2-2m-3为奇数,解得m=0,或m=2,则实数m的取值集合为{0,2}.
12.答案:f(x)=x3 [0,27]
解析:因为m∈{x|-2
当m=1时,f(x)=x0,条件(1)(2)都不满足;
当m=0时,f(x)=x3,条件(1)(2)都满足,且在区间[0,3]上是增函数,所以x∈[0,3]时,函数f(x)的值域为[0,27].
13.答案:1
解析:因为BM=MN=NA,点A(1,0),点B(0,1),
所以M(,),N(,),分别代入y=xα,y=xβ,
则α=log,β=log,
所以α·β=log·log=1.
14.答案:(1)16 (2)-1或-
解析:(1)由m2-5m+7=1,得m=2或3,
当m=2时,f(x)=x-3是奇函数,∴不满足题意,
∴m=2舍去;
当m=3时,f(x)=x-4,满足题意,
∴f(x)=x-4,
∴f()=()-4=16.
(2)由f(x)=x-4为偶函数和f(2a+1)=f(a)可得|2a+1|=|a|,即2a+1=a或2a+1=-a,解得a=-1或a=-.
