探索直线平行的条件(1)[下学期]
文档属性
| 名称 | 探索直线平行的条件(1)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 583.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-07 19:29:00 | ||
图片预览

文档简介
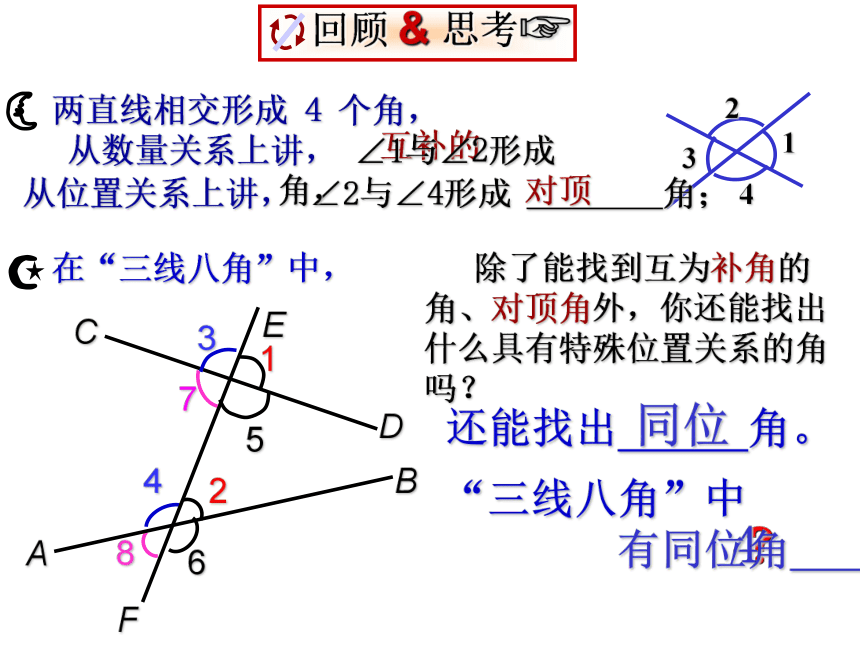
课件21张PPT。5.2.2直线平行的条件 我们知道平面内不相交的两条直线互相平行,又知道都与第三条直线平行的两条直线平行。我们可以用这些方法来判断两条直线平行。那除此以外还有没有其它的方法呢?这节课我们一起来探索直线平行的条件。回顾与思考两直线相交形成 4 个角,1234互补的从位置关系上讲, ∠2与∠4形成 角;对顶 除了能找到互为补角的角、对顶角外,你还能找出 什么具有特殊位置关系的角吗?还能找出 角。 同位4 “三线八角”中
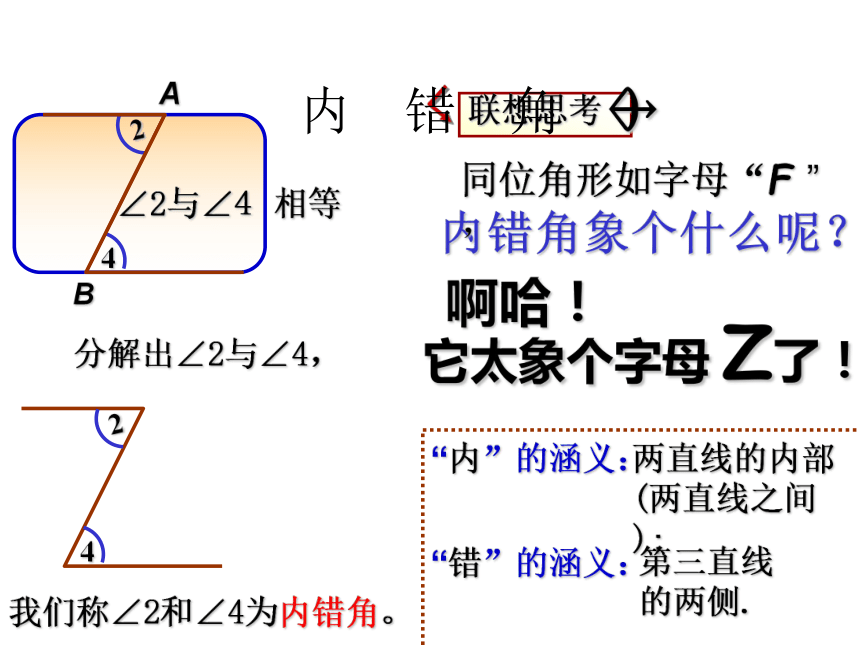
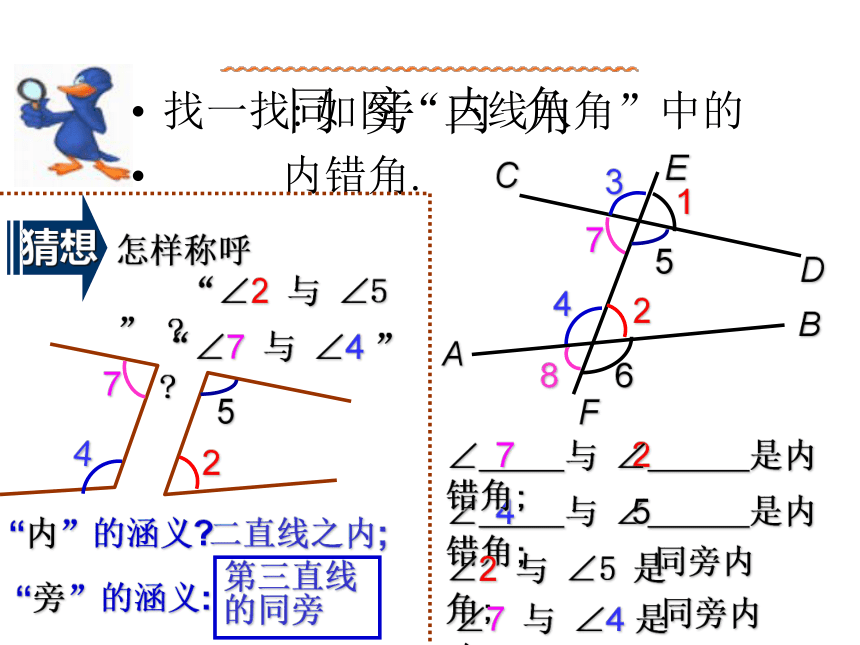
有同位角 组。 从数量关系上讲, ∠1与∠2形成 角,∠2与∠4相等分解出∠2与∠4,内错角象个什么呢?啊哈!我们称∠2和∠4为内错角。它太象个字母 Z了!内 错 角两直线的内部(两直线之间);“错”的涵义:第三直线的两侧.同 旁 内 角72∠ 与 ∠ 是内错角;45同旁内同旁内找一找: 如图“三线八角”中的
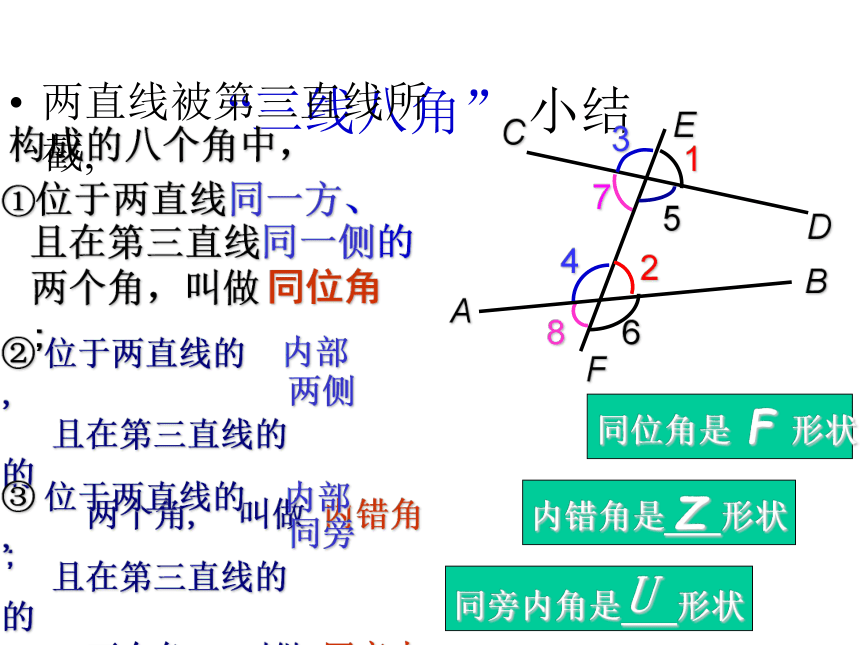
内错角.“内”的涵义?“旁”的涵义:二直线之内;第三直线的同旁“三线八角” 小结构成的八个角中, 两直线被第三直线所截, ①位于两直线同一方、 ② 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 内错角 ; 且在第三直线同一侧的
两个角,叫做 ; 同位角内部两侧③ 位于两直线的 ,
且在第三直线的 的
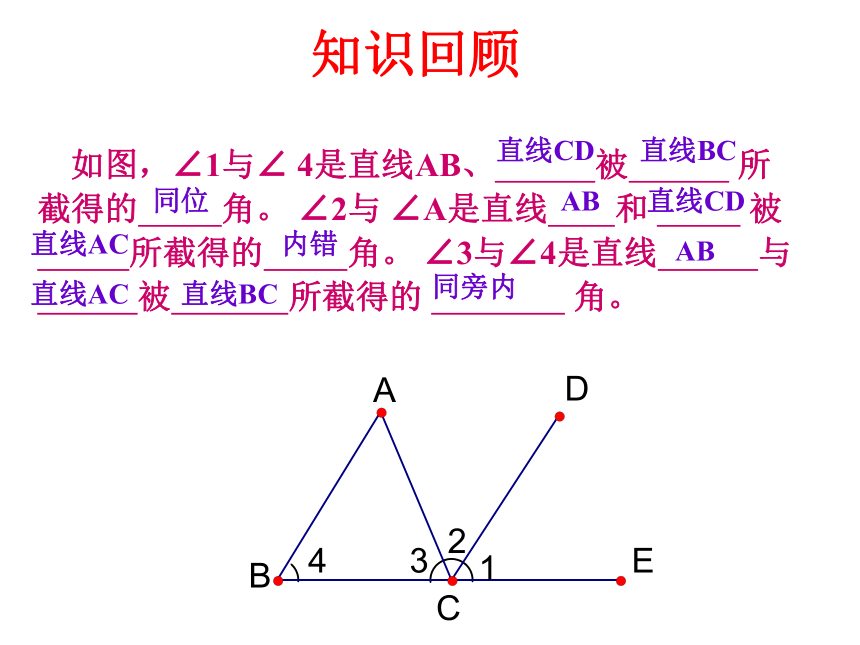
两个角, 叫做 同旁内角 ; 内部同旁ZU知识回顾 如图,∠1与∠ 4是直线AB、 被 所
截得的 角。 ∠2与 ∠A是直线 和 被
所截得的 角。 ∠3与∠4是直线 与
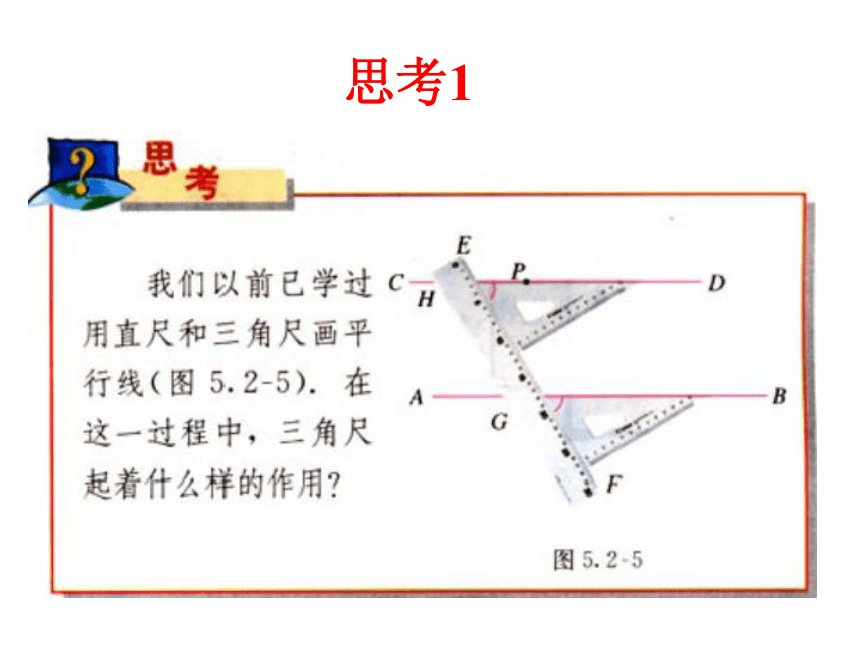
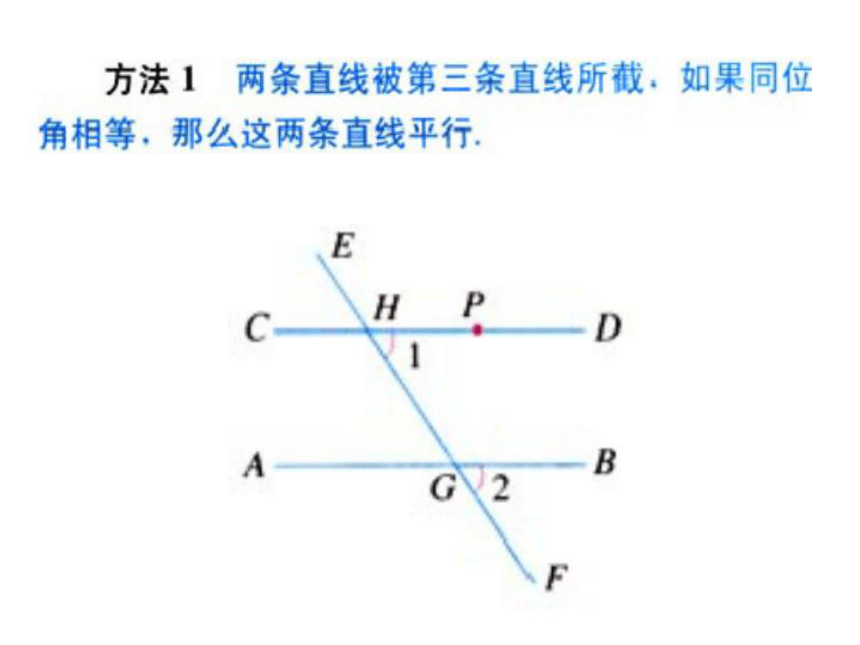
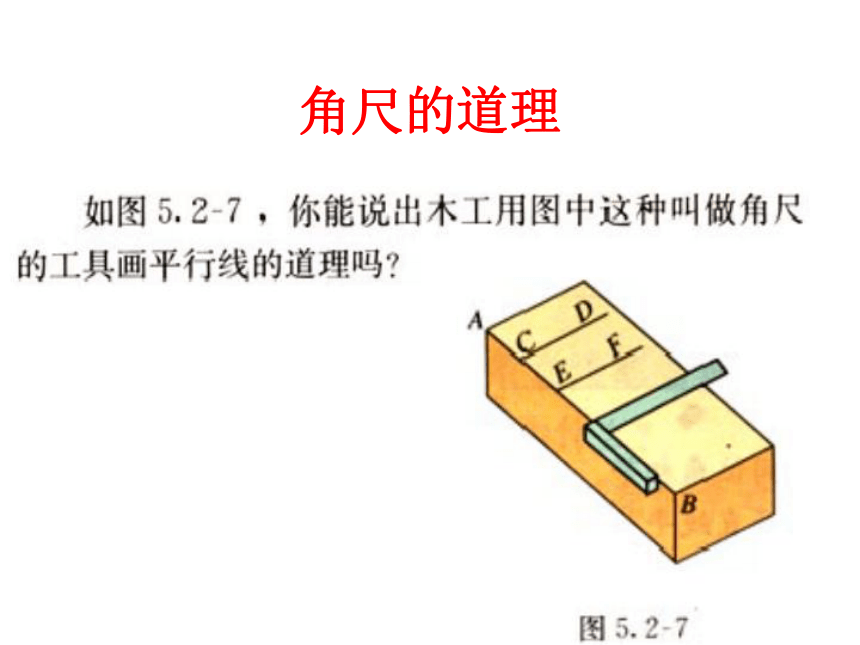
被 所截得的 角。直线CD直线BC同位AB直线CD直线AC内错AB直线AC直线BC同旁内思考1方法一角尺的道理cab124、及时巩固,及时反馈证明:∴∠1=∠2 (等量代换)∴a∥b (同位角相等、两直线平行)。练习1:
如图练习2:
如图5、讨论练习、巩固定理1、如图, BE是AB的延长线.
量得 ∠CBE=∠A从∠CBE=∠A ,可以判定哪两条直
线平行 ? 它的根据是什么?证明: ∵∠CBE=∠A (已知)∴AD∥BC (同位角相等、两直线平行)思考2方法二方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。例3:如图, ∠A= 55 °, ∠B=125 °,AD
与BC平行吗?AB与CD平行吗?为什么?DABC[ 根据题目中现有的条件,无法判断AB与CD平行。]解:因为∠1= 70 °,
所以∠3=110 °( ∠1 与∠3互补)
因为∠2 =∠3=110 °
所以AD//BC (内错角相等,两直线平行。)4填空:
如图,直线CD与EF被直线AB所截。
如果∠1= ∠3,那么CD与EF平行。
因为∠1= ∠3(__________),
又因为∠2= ∠3(__________),
所以∠1= ∠2(________),
___________(同位角相等,两直线平行。)
已知对顶角相等等量代换CD//EF132CDEFAB归纳练习1 1、观察右图并填空:
(1) ∠1 与 是同位角; (2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角; 随堂练习p 57banm23145∠4∠3∠2a∥b.l∥m.l∥n .练习21、如图,若∠2= ∠ 5,可以判定哪两条直线平行?根据是什么?
2、若∠ 1+ ∠3=180°,可以判定哪两条直线平行?根据是什么?3、若∠ 2= ∠ 4,可以判定哪两条直线平行?根据是什么?4、若∠ 3+ ∠ 5=180°,可以判定哪两条直线平行?根据是什么?
再 见
有同位角 组。 从数量关系上讲, ∠1与∠2形成 角,∠2与∠4相等分解出∠2与∠4,内错角象个什么呢?啊哈!我们称∠2和∠4为内错角。它太象个字母 Z了!内 错 角两直线的内部(两直线之间);“错”的涵义:第三直线的两侧.同 旁 内 角72∠ 与 ∠ 是内错角;45同旁内同旁内找一找: 如图“三线八角”中的
内错角.“内”的涵义?“旁”的涵义:二直线之内;第三直线的同旁“三线八角” 小结构成的八个角中, 两直线被第三直线所截, ①位于两直线同一方、 ② 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 内错角 ; 且在第三直线同一侧的
两个角,叫做 ; 同位角内部两侧③ 位于两直线的 ,
且在第三直线的 的
两个角, 叫做 同旁内角 ; 内部同旁ZU知识回顾 如图,∠1与∠ 4是直线AB、 被 所
截得的 角。 ∠2与 ∠A是直线 和 被
所截得的 角。 ∠3与∠4是直线 与
被 所截得的 角。直线CD直线BC同位AB直线CD直线AC内错AB直线AC直线BC同旁内思考1方法一角尺的道理cab124、及时巩固,及时反馈证明:∴∠1=∠2 (等量代换)∴a∥b (同位角相等、两直线平行)。练习1:
如图练习2:
如图5、讨论练习、巩固定理1、如图, BE是AB的延长线.
量得 ∠CBE=∠A从∠CBE=∠A ,可以判定哪两条直
线平行 ? 它的根据是什么?证明: ∵∠CBE=∠A (已知)∴AD∥BC (同位角相等、两直线平行)思考2方法二方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。例3:如图, ∠A= 55 °, ∠B=125 °,AD
与BC平行吗?AB与CD平行吗?为什么?DABC[ 根据题目中现有的条件,无法判断AB与CD平行。]解:因为∠1= 70 °,
所以∠3=110 °( ∠1 与∠3互补)
因为∠2 =∠3=110 °
所以AD//BC (内错角相等,两直线平行。)4填空:
如图,直线CD与EF被直线AB所截。
如果∠1= ∠3,那么CD与EF平行。
因为∠1= ∠3(__________),
又因为∠2= ∠3(__________),
所以∠1= ∠2(________),
___________(同位角相等,两直线平行。)
已知对顶角相等等量代换CD//EF132CDEFAB归纳练习1 1、观察右图并填空:
(1) ∠1 与 是同位角; (2) ∠5 与 是同旁内角;
(3) ∠1 与 是内错角; 随堂练习p 57banm23145∠4∠3∠2a∥b.l∥m.l∥n .练习21、如图,若∠2= ∠ 5,可以判定哪两条直线平行?根据是什么?
2、若∠ 1+ ∠3=180°,可以判定哪两条直线平行?根据是什么?3、若∠ 2= ∠ 4,可以判定哪两条直线平行?根据是什么?4、若∠ 3+ ∠ 5=180°,可以判定哪两条直线平行?根据是什么?
再 见
