沪科版九年级上册数学第一次月考试卷(含答案)
文档属性
| 名称 | 沪科版九年级上册数学第一次月考试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 00:05:40 | ||
图片预览


文档简介
沪科版九年级上册数学第一次月考试题
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列表达式中,是的二次函数的是( )
A. B.
C. D.
2.若反比例函数y=(k≠0)的图象与函数y=-4x的图象的一个交点坐标为(-1,4),则另一个交点的坐标是( )
A.(4,-1) B.(-1,-4) C.(-4,1) D.(1,-4)
3.已知点在抛物线上,则下列结论正确的是( )
A. B. C. D.
4.二次函数的图象如图所示,对称轴为直线,下列结论不正确的是( )
A. B.当时,顶点的坐标为
C.当时, D.当时,y随x的增大而增大
5.反比例函数图象上的两上点为,,且,则下列关系成立的是( )
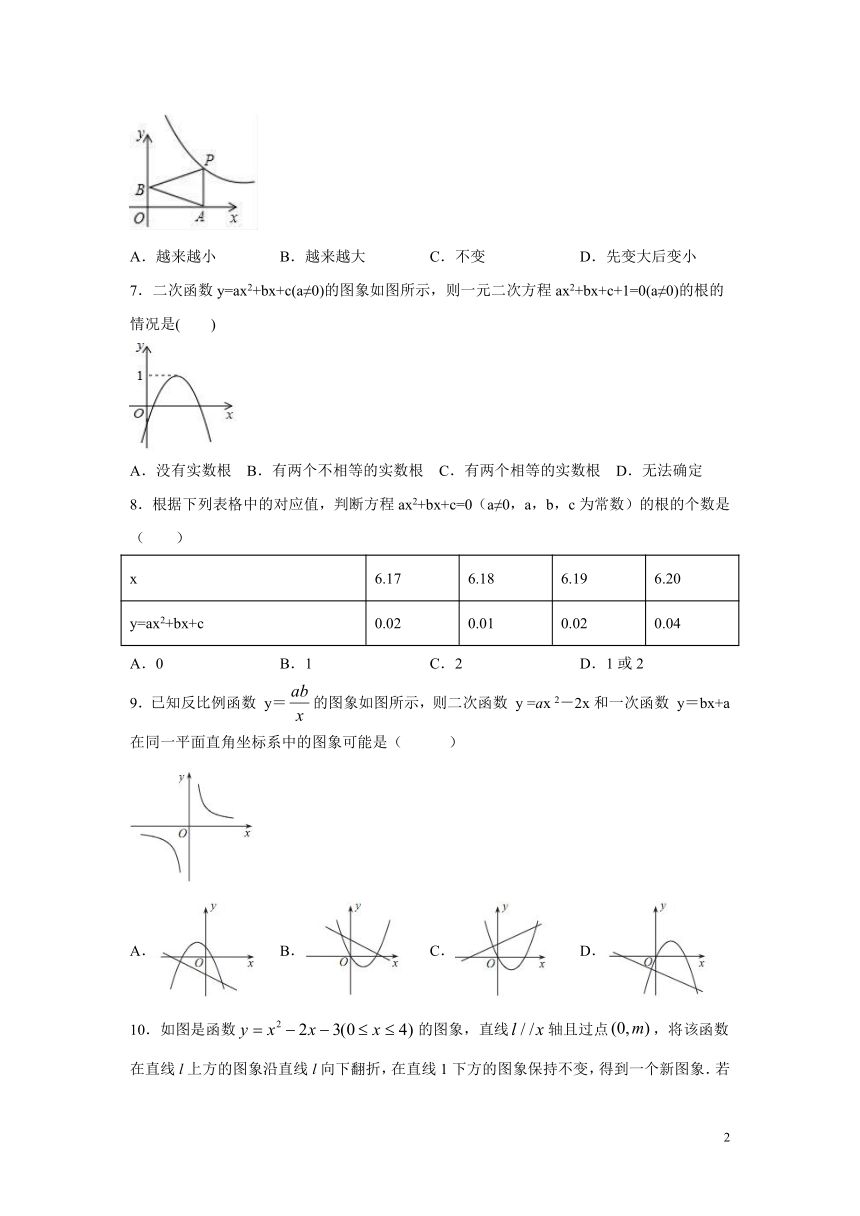
A.y1>y2 B.y16.如图,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数(x>0)图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会( )
A.越来越小 B.越来越大 C.不变 D.先变大后变小
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一元二次方程ax2+bx+c+1=0(a≠0)的根的情况是( )
A.没有实数根 B.有两个不相等的实数根 C.有两个相等的实数根 D.无法确定
8.根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是 ( )
x 6.17 6.18 6.19 6.20
y=ax2+bx+c 0.02 0.01 0.02 0.04
A.0 B.1 C.2 D.1或2
9.已知反比例函数 y=的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
10.如图是函数的图象,直线轴且过点,将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A. B. C. D.或
二、填空题。(每小题4分,共16分)
11.已知二次函数,则它的图象与y轴的交点坐标为_____.
12.对于二次函数y=x2﹣2mx﹣3,当x=2时的函数值与x=8时的函数值相等时,m=_____
13.如图,点A是反比例函数的图象上任意一点,AB∥x轴交反比例函数 的图象于点B,以AB为边作,其中C,D在x轴上,若的面积为3,则的值为______.
14.已知二次函数y=a(x﹣m)2﹣m+1(a、m为常数且a<0),下列结论:
①这个函数图象的顶点始终在直线y=﹣x+1上;
②a(x-1)(x+3)=﹣1有两个根x1和x2,且x1<x2,则﹣3<x1<x2<1;
③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2≥2m,则y1≤y2;
④当﹣1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.
其中正确结论的序号是____________.
三、解答题
15.(10分)已知抛物线y=ax2+6x-8与直线y=-3x相交于点A(1,m).
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到y=ax2的图象.
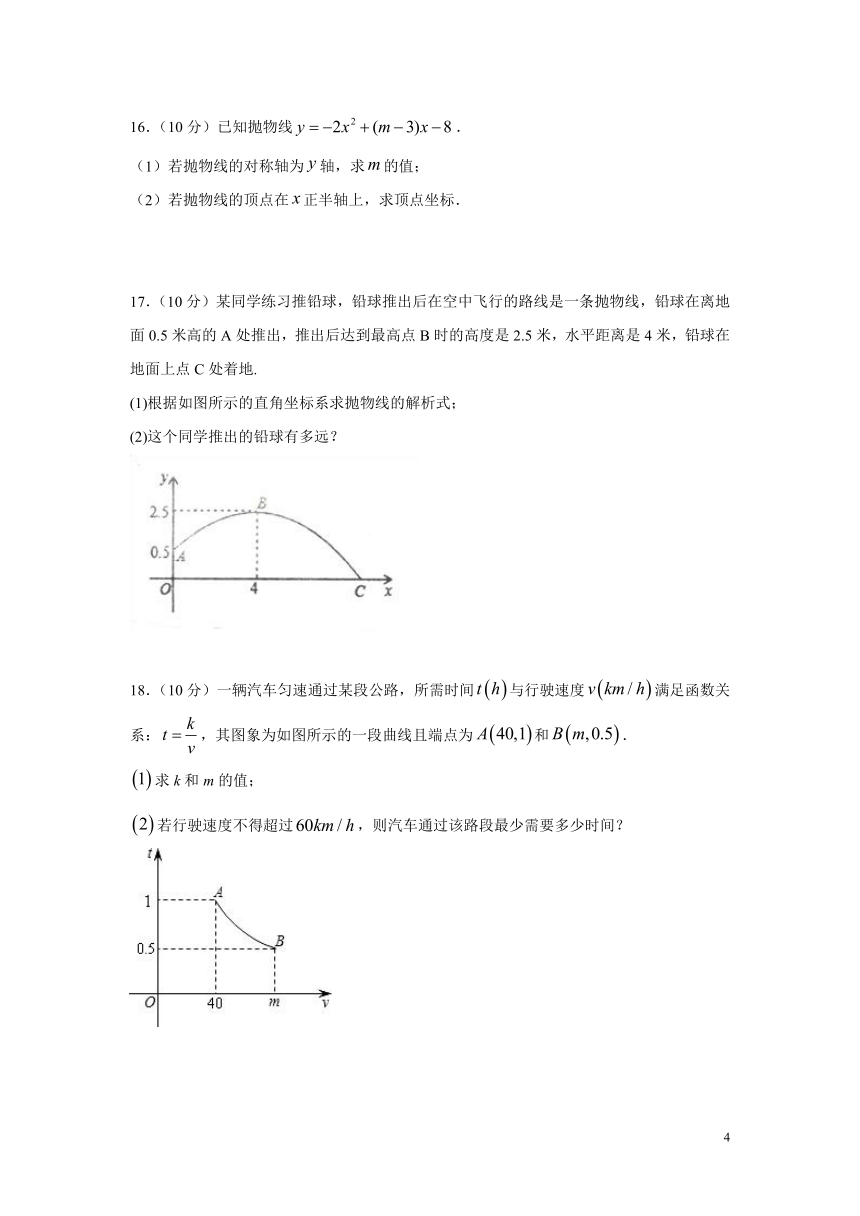
16.(10分)已知抛物线.
(1)若抛物线的对称轴为轴,求的值;
(2)若抛物线的顶点在正半轴上,求顶点坐标.
17.(10分)某同学练习推铅球,铅球推出后在空中飞行的路线是一条抛物线,铅球在离地面0.5米高的A处推出,推出后达到最高点B时的高度是2.5米,水平距离是4米,铅球在地面上点C处着地.
(1)根据如图所示的直角坐标系求抛物线的解析式;
(2)这个同学推出的铅球有多远?
18.(10分)一辆汽车匀速通过某段公路,所需时间与行驶速度满足函数关系:,其图象为如图所示的一段曲线且端点为和.
求k和m的值;
若行驶速度不得超过,则汽车通过该路段最少需要多少时间?
19.(10分)已知二次函数
如果二次函数的图象与x轴有两个交点,求m的取值范围;
如图,二次函数的图象过,点,与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
20.(10分)如图隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)该隧道内设双行道,一辆货车高4m,宽2.5m,能否安全通过,为什么?
21.(12分)如图,在平面直角坐标系中,一次函数的图象与反比例函数 的图象相交于第一、三象限内的两点,与轴交于点
⑴求该反比例函数和一次函数的解析式;
⑵在轴上找一点使最大,求的最大值及点的坐标;
⑶直接写出当时,的取值范围.
22.(10分)如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式
(2)若点M是位于直线AB上方抛物线上的一动点,当的面积最大时,求此时的面积S及点M的坐标.
23.(12分)某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 每天工人数(人) 每天产量(件) 每件产品可获利润(元)
甲 15
乙
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
参考答案
1.B
2.D
3.A
4.C
5.D
6.C
7.B
8.A
9.C
10.C
11.(0,-2)
12.5
13.-1
14.①④
15.(1) y=-x2+6x-8;(2) 把抛物线y=-x2+6x-8向左平移3个单位再向下平移1个单位得到y=-x2的图象
16.(1)3;(2)
17.(1) (2)
18.(1)k=40,m=80;(2)汽车通过该路段最少需要小时.
19.(1)且;(2)P点坐标为.
20.(1) y=x2+2x+2,拱顶D到地面OA的距离为6m;(2)能,见解析
21.⑴,;⑵的最大值为, ;⑶或.
22.(1) y=﹣x2+2x+3;(2) △MAB的面积最大值是,M(,)
23.(1)填表见解析;(2)每件乙产品可获得的利润是110元;(3)安排26人生产乙产品时,可获得的最大总利润为3198元.
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列表达式中,是的二次函数的是( )
A. B.
C. D.
2.若反比例函数y=(k≠0)的图象与函数y=-4x的图象的一个交点坐标为(-1,4),则另一个交点的坐标是( )
A.(4,-1) B.(-1,-4) C.(-4,1) D.(1,-4)
3.已知点在抛物线上,则下列结论正确的是( )
A. B. C. D.
4.二次函数的图象如图所示,对称轴为直线,下列结论不正确的是( )
A. B.当时,顶点的坐标为
C.当时, D.当时,y随x的增大而增大
5.反比例函数图象上的两上点为,,且,则下列关系成立的是( )
A.y1>y2 B.y1
A.越来越小 B.越来越大 C.不变 D.先变大后变小
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一元二次方程ax2+bx+c+1=0(a≠0)的根的情况是( )
A.没有实数根 B.有两个不相等的实数根 C.有两个相等的实数根 D.无法确定
8.根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是 ( )
x 6.17 6.18 6.19 6.20
y=ax2+bx+c 0.02 0.01 0.02 0.04
A.0 B.1 C.2 D.1或2
9.已知反比例函数 y=的图象如图所示,则二次函数 y =ax 2-2x和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
10.如图是函数的图象,直线轴且过点,将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A. B. C. D.或
二、填空题。(每小题4分,共16分)
11.已知二次函数,则它的图象与y轴的交点坐标为_____.
12.对于二次函数y=x2﹣2mx﹣3,当x=2时的函数值与x=8时的函数值相等时,m=_____
13.如图,点A是反比例函数的图象上任意一点,AB∥x轴交反比例函数 的图象于点B,以AB为边作,其中C,D在x轴上,若的面积为3,则的值为______.
14.已知二次函数y=a(x﹣m)2﹣m+1(a、m为常数且a<0),下列结论:
①这个函数图象的顶点始终在直线y=﹣x+1上;
②a(x-1)(x+3)=﹣1有两个根x1和x2,且x1<x2,则﹣3<x1<x2<1;
③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2≥2m,则y1≤y2;
④当﹣1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.
其中正确结论的序号是____________.
三、解答题
15.(10分)已知抛物线y=ax2+6x-8与直线y=-3x相交于点A(1,m).
(1)求抛物线的解析式;
(2)请问(1)中的抛物线经过怎样的平移就可以得到y=ax2的图象.
16.(10分)已知抛物线.
(1)若抛物线的对称轴为轴,求的值;
(2)若抛物线的顶点在正半轴上,求顶点坐标.
17.(10分)某同学练习推铅球,铅球推出后在空中飞行的路线是一条抛物线,铅球在离地面0.5米高的A处推出,推出后达到最高点B时的高度是2.5米,水平距离是4米,铅球在地面上点C处着地.
(1)根据如图所示的直角坐标系求抛物线的解析式;
(2)这个同学推出的铅球有多远?
18.(10分)一辆汽车匀速通过某段公路,所需时间与行驶速度满足函数关系:,其图象为如图所示的一段曲线且端点为和.
求k和m的值;
若行驶速度不得超过,则汽车通过该路段最少需要多少时间?
19.(10分)已知二次函数
如果二次函数的图象与x轴有两个交点,求m的取值范围;
如图,二次函数的图象过,点,与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
20.(10分)如图隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)该隧道内设双行道,一辆货车高4m,宽2.5m,能否安全通过,为什么?
21.(12分)如图,在平面直角坐标系中,一次函数的图象与反比例函数 的图象相交于第一、三象限内的两点,与轴交于点
⑴求该反比例函数和一次函数的解析式;
⑵在轴上找一点使最大,求的最大值及点的坐标;
⑶直接写出当时,的取值范围.
22.(10分)如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式
(2)若点M是位于直线AB上方抛物线上的一动点,当的面积最大时,求此时的面积S及点M的坐标.
23.(12分)某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 每天工人数(人) 每天产量(件) 每件产品可获利润(元)
甲 15
乙
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
参考答案
1.B
2.D
3.A
4.C
5.D
6.C
7.B
8.A
9.C
10.C
11.(0,-2)
12.5
13.-1
14.①④
15.(1) y=-x2+6x-8;(2) 把抛物线y=-x2+6x-8向左平移3个单位再向下平移1个单位得到y=-x2的图象
16.(1)3;(2)
17.(1) (2)
18.(1)k=40,m=80;(2)汽车通过该路段最少需要小时.
19.(1)且;(2)P点坐标为.
20.(1) y=x2+2x+2,拱顶D到地面OA的距离为6m;(2)能,见解析
21.⑴,;⑵的最大值为, ;⑶或.
22.(1) y=﹣x2+2x+3;(2) △MAB的面积最大值是,M(,)
23.(1)填表见解析;(2)每件乙产品可获得的利润是110元;(3)安排26人生产乙产品时,可获得的最大总利润为3198元.
(
2
)
(
1
)
同课章节目录
