2023秋人教版二年级数学上册 数学广角《搭配(一)》(课件)(共22张PPT)
文档属性
| 名称 | 2023秋人教版二年级数学上册 数学广角《搭配(一)》(课件)(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
2023秋 人教数学
二年级上册
数学广角《搭配(一)》
人教版二年级上册第八单元
复习导入
2
1
2
1
森林王国的密码是由1和2组成的。
探究新知
用数字1、2、3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
森林王国选国王啦,要答对下面的题才可以!
有3个,国王是我!
和 ,谁才能当上国王呢?
是6个才对,国王是我!
探究新知
用数字1、2、3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
想一想:已知什么?要求什么?
探究新知
1
2
3
1
3
2
3
……
2
1
2
1
我也用卡片摆一摆。
摆得太乱了。怎样才能做到不重不漏写出所有数呢?
我发现1和2可以组成不同的两位数。
探究新知
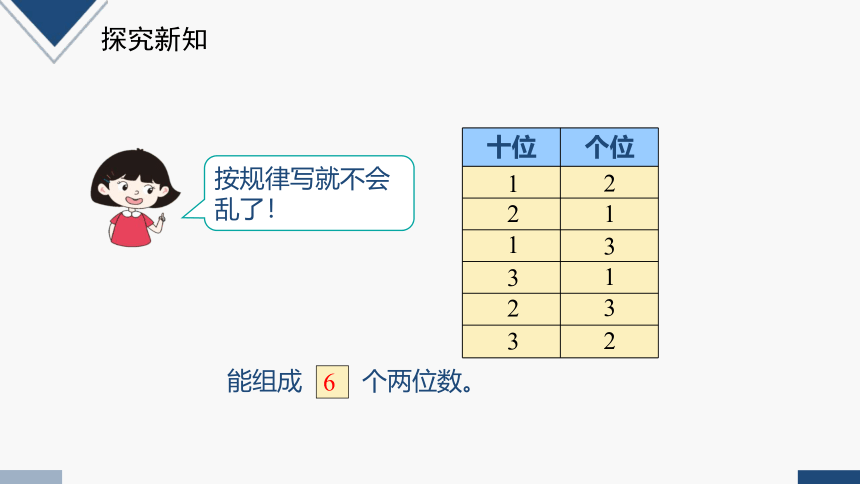
按规律写就不会乱了!
十位 个位
1
2
2
1
1
3
3
1
2
3
3
2
能组成 个两位数。
6
探究新知
十位 个位
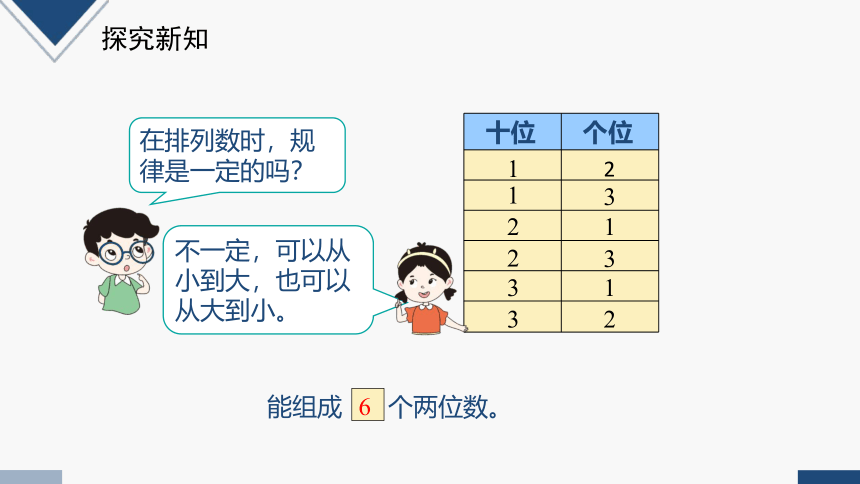
不一定,可以从小到大,也可以从大到小。
在排列数时,规律是一定的吗?
1
2
1
3
2
1
2
3
3
1
3
2
能组成 个两位数。
6
探究新知
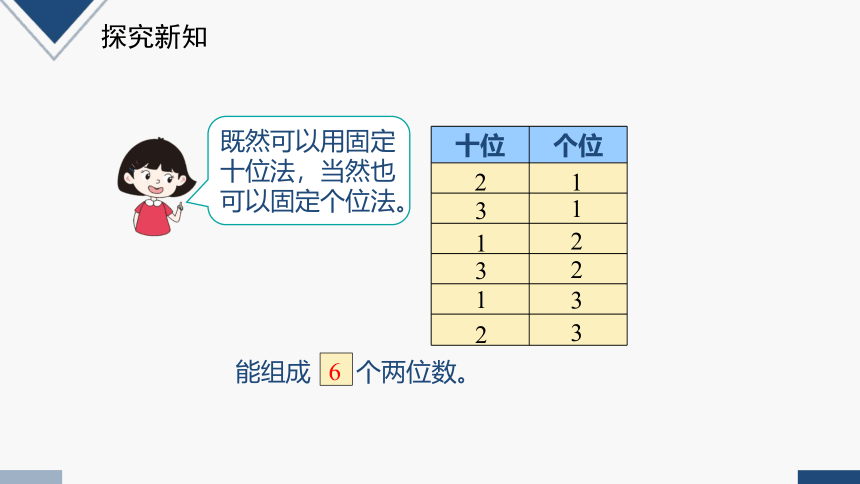
既然可以用固定十位法,当然也可以固定个位法。
十位 个位
能组成 个两位数。
6
1
2
1
3
2
1
2
3
3
1
3
2
探究新知
十位 个位
1
2
2
1
1
3
3
1
2
3
3
2
交换位置法
十位 个位
1
2
1
3
2
1
2
3
3
1
3
2
固定十位法
十位 个位
1
2
1
3
2
1
2
3
3
1
3
2
固定个位法
想一想、比一比,这几种方法有什么共同的地方?
不论哪种方法,都是按一定的顺序进行思考,这些都是有序思考的方法。
探究新知
我是国王
探究新知
有3个数1、2、3,任意选取其中2个求和,得数有几种可能?
想一想:已知什么?要求什么?
探究新知
列算式
1+2=3
2+1=3
1+3=4
3+1=4
2+3=5
3+2=5
得数有3种可能。
探究新知
加数 加数 和
1
2
2
3
1
4
3
4
2
5
3
5
3
1
1
3
3
2
列表格
去掉重复的情况,有3种可能。
探究新知
得数有 种可能。
3
2
3
1
3
5
4
连一连
两个数的和与顺序没有关系!
探究新知
从3个数中任选其中两个数求和,得数有3种情况,与加数的顺序没有关系。
两个数求和时,交换加数的位置后,和不会改变,也就是说和与加数的顺序没有关系,得数算1种情况。
两个数相加得到的和,如“1+2=3”“2+1=3”这两个算式的和都是3,和应该算1种情况。
探究新知
用1、2、3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
有3个数1、2、3,任意选取其中2个求和,得数有几种可能?
比一比,这两题有什么相同点与不同点?
探究新知
总结:
用两个数字组数,只要把两个数字调换位置,组成的两个数就不同,而两个数的和,无论两个数怎样调换位置,和都不变,和与数的位置顺序没有关系。当然,有序思考才能做到既不重复也不遗漏!
课堂练习
北城 南城
1.用 、 和 3种颜色给地图上的两个城区图上不同的颜色,一共有多少种涂色方法?
一共有6种涂色方法。
课堂练习
2.每两个人握1次手,3人一共握几次手?
3人一共握了3次手。
课堂小结
这节课你有什么收获?
谢谢观看
2023秋 人教数学
二年级上册
数学广角《搭配(一)》
人教版二年级上册第八单元
复习导入
2
1
2
1
森林王国的密码是由1和2组成的。
探究新知
用数字1、2、3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
森林王国选国王啦,要答对下面的题才可以!
有3个,国王是我!
和 ,谁才能当上国王呢?
是6个才对,国王是我!
探究新知
用数字1、2、3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
想一想:已知什么?要求什么?
探究新知
1
2
3
1
3
2
3
……
2
1
2
1
我也用卡片摆一摆。
摆得太乱了。怎样才能做到不重不漏写出所有数呢?
我发现1和2可以组成不同的两位数。
探究新知
按规律写就不会乱了!
十位 个位
1
2
2
1
1
3
3
1
2
3
3
2
能组成 个两位数。
6
探究新知
十位 个位
不一定,可以从小到大,也可以从大到小。
在排列数时,规律是一定的吗?
1
2
1
3
2
1
2
3
3
1
3
2
能组成 个两位数。
6
探究新知
既然可以用固定十位法,当然也可以固定个位法。
十位 个位
能组成 个两位数。
6
1
2
1
3
2
1
2
3
3
1
3
2
探究新知
十位 个位
1
2
2
1
1
3
3
1
2
3
3
2
交换位置法
十位 个位
1
2
1
3
2
1
2
3
3
1
3
2
固定十位法
十位 个位
1
2
1
3
2
1
2
3
3
1
3
2
固定个位法
想一想、比一比,这几种方法有什么共同的地方?
不论哪种方法,都是按一定的顺序进行思考,这些都是有序思考的方法。
探究新知
我是国王
探究新知
有3个数1、2、3,任意选取其中2个求和,得数有几种可能?
想一想:已知什么?要求什么?
探究新知
列算式
1+2=3
2+1=3
1+3=4
3+1=4
2+3=5
3+2=5
得数有3种可能。
探究新知
加数 加数 和
1
2
2
3
1
4
3
4
2
5
3
5
3
1
1
3
3
2
列表格
去掉重复的情况,有3种可能。
探究新知
得数有 种可能。
3
2
3
1
3
5
4
连一连
两个数的和与顺序没有关系!
探究新知
从3个数中任选其中两个数求和,得数有3种情况,与加数的顺序没有关系。
两个数求和时,交换加数的位置后,和不会改变,也就是说和与加数的顺序没有关系,得数算1种情况。
两个数相加得到的和,如“1+2=3”“2+1=3”这两个算式的和都是3,和应该算1种情况。
探究新知
用1、2、3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
有3个数1、2、3,任意选取其中2个求和,得数有几种可能?
比一比,这两题有什么相同点与不同点?
探究新知
总结:
用两个数字组数,只要把两个数字调换位置,组成的两个数就不同,而两个数的和,无论两个数怎样调换位置,和都不变,和与数的位置顺序没有关系。当然,有序思考才能做到既不重复也不遗漏!
课堂练习
北城 南城
1.用 、 和 3种颜色给地图上的两个城区图上不同的颜色,一共有多少种涂色方法?
一共有6种涂色方法。
课堂练习
2.每两个人握1次手,3人一共握几次手?
3人一共握了3次手。
课堂小结
这节课你有什么收获?
谢谢观看
