2.3 幂函数(全课时,讲练结合,共33页PPT)
文档属性
| 名称 | 2.3 幂函数(全课时,讲练结合,共33页PPT) | 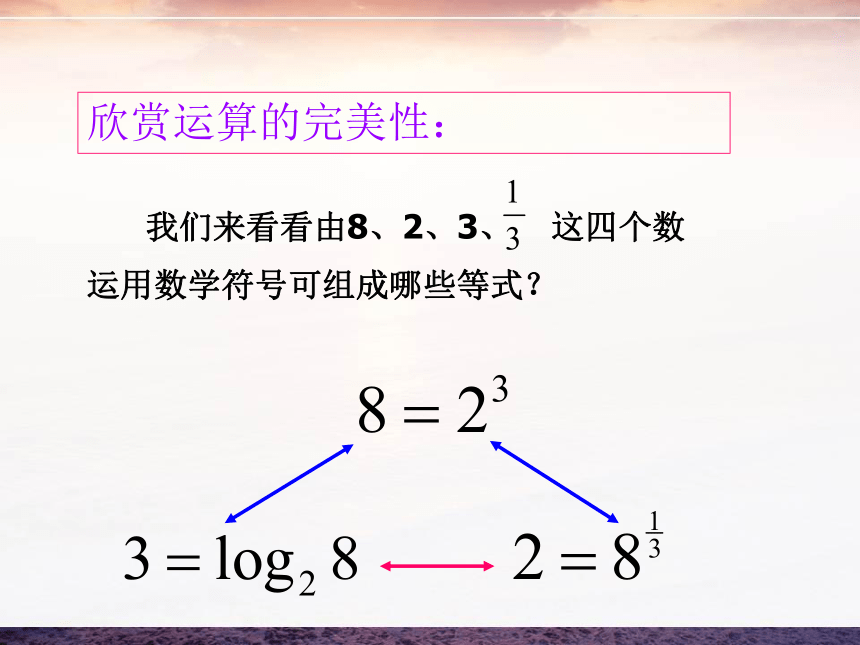 | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-11 09:02:46 | ||
图片预览











文档简介
课件33张PPT。欣赏运算的完美性: 我们来看看由8、2、3、 这四个数
运用数学符号可组成哪些等式?我们知道:函数的完美追求设想:2.3 幂函数问 题y = xy = x22018年12月23日1y = x3以上问题中的函数有什么共同特征?(1)都是函数;
(2)均是以自变量为底的幂;
(3)指数为常数;
(4)幂前的系数也为1。
上述问题中涉及的函数,都是形如
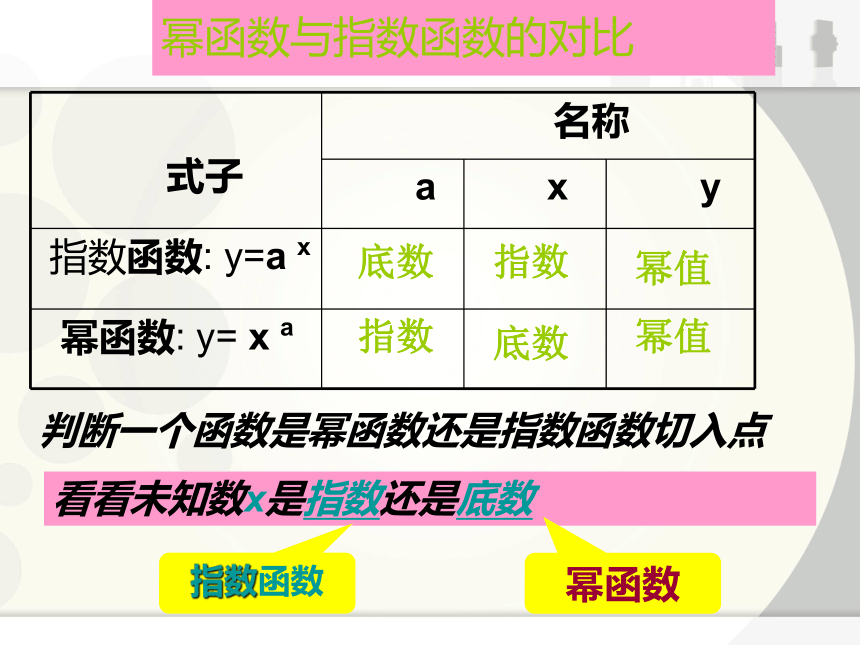
的函数幂函数的一般概念: 一般地,函数 幂函数的结构特征你能说出幂函数与指数函数的区别吗?3. 幂前的系数也为11.自变量为底2.指数为常数叫做幂函数,其中x为自变量,a为常数。底数
指数指数
底数
幂值幂值幂函数与指数函数的对比判断一个函数是幂函数还是指数函数切入点看看未知数x是指数还是底数幂函数指数函数
练习、下面几个函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=x2 + x (4)y=1
(5)y = 2x 答案(1)(4)P79练习1定义几点说明:1、对于幂函数,课本只讨论 =1,2,3, ,-1时的情形。2、幂函数不象指数函数和对数函数,其定义域
随 的不同而不同。下面研究幂函数 研究图象的性质,一般包括:定义域、值域、单调性、奇偶性、过定点的情况等研究 。函数图象的画法是:列表描点连线作出下列函数的图象:作出下列函数的图象:(1,1)(2,4)(-2,4)(-1,1)(-1,-1)从图象能得出他们的性质吗?探究:结合以上分析及幂函数图象(课本第78页图2.3-1),填写课本第78页表格:RR奇函数奇函数非奇非偶函数奇函数R上是增函数R上是增函数在 上是增函数RRR偶函数在
上是减函数(1,1)一般幂函数的性质:★所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1).
★如果α>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数.
★如果α<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数.
★当α为奇数时,幂函数为奇函数,
★当α为偶数时,幂函数为偶函数.
★幂函数的定义域、奇偶性,单调性,
因函数式中α的不同而各异.4.关于x的函数y=(x-1)α(其中α的取值范围可以是1,2,3,-1,1/2)的图象恒过点________.解析:当x-1=1,即x=2时,无论α取何值,均有1α=1,
∴函数y=(x-1)α恒过点(2,1).
答案:(2,1)【例1】 已知函数f(x)=(m2+2m)·xm2+m-1,m为何值时,f(x)是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.
1.函数f(x)=(m2-m-1)xm2+m-3是幂函数且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.
解:根据幂函数的定义,得m2-m-1=1,
解得m=2或m=-1,
当m=2时,f(x)=x3在(0,+∞)上是增函数;
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,不符合要求.故f(x)=x3.补上后两题①②③沿箭头方向指数由小到大yox-12211沿箭头方向指数由小到大答案:D证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例1证明:任取所以幂函数 在[0,+∞)上是增函数.方法技巧:分子有理化除了作差,还有没有其它方法呢? 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; 证明幂函数 在[0,+∞)上是增函数.(1)作差法:若给出的函数是有根号的式子,往往采用有理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以
运用数学符号可组成哪些等式?我们知道:函数的完美追求设想:2.3 幂函数问 题y = xy = x22018年12月23日1y = x3以上问题中的函数有什么共同特征?(1)都是函数;
(2)均是以自变量为底的幂;
(3)指数为常数;
(4)幂前的系数也为1。
上述问题中涉及的函数,都是形如
的函数幂函数的一般概念: 一般地,函数 幂函数的结构特征你能说出幂函数与指数函数的区别吗?3. 幂前的系数也为11.自变量为底2.指数为常数叫做幂函数,其中x为自变量,a为常数。底数
指数指数
底数
幂值幂值幂函数与指数函数的对比判断一个函数是幂函数还是指数函数切入点看看未知数x是指数还是底数幂函数指数函数
练习、下面几个函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=x2 + x (4)y=1
(5)y = 2x 答案(1)(4)P79练习1定义几点说明:1、对于幂函数,课本只讨论 =1,2,3, ,-1时的情形。2、幂函数不象指数函数和对数函数,其定义域
随 的不同而不同。下面研究幂函数 研究图象的性质,一般包括:定义域、值域、单调性、奇偶性、过定点的情况等研究 。函数图象的画法是:列表描点连线作出下列函数的图象:作出下列函数的图象:(1,1)(2,4)(-2,4)(-1,1)(-1,-1)从图象能得出他们的性质吗?探究:结合以上分析及幂函数图象(课本第78页图2.3-1),填写课本第78页表格:RR奇函数奇函数非奇非偶函数奇函数R上是增函数R上是增函数在 上是增函数RRR偶函数在
上是减函数(1,1)一般幂函数的性质:★所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1).
★如果α>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数.
★如果α<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数.
★当α为奇数时,幂函数为奇函数,
★当α为偶数时,幂函数为偶函数.
★幂函数的定义域、奇偶性,单调性,
因函数式中α的不同而各异.4.关于x的函数y=(x-1)α(其中α的取值范围可以是1,2,3,-1,1/2)的图象恒过点________.解析:当x-1=1,即x=2时,无论α取何值,均有1α=1,
∴函数y=(x-1)α恒过点(2,1).
答案:(2,1)【例1】 已知函数f(x)=(m2+2m)·xm2+m-1,m为何值时,f(x)是:(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数.
1.函数f(x)=(m2-m-1)xm2+m-3是幂函数且当x∈(0,+∞)时,f(x)是增函数,求f(x)的解析式.
解:根据幂函数的定义,得m2-m-1=1,
解得m=2或m=-1,
当m=2时,f(x)=x3在(0,+∞)上是增函数;
当m=-1时,f(x)=x-3在(0,+∞)上是减函数,不符合要求.故f(x)=x3.补上后两题①②③沿箭头方向指数由小到大yox-12211沿箭头方向指数由小到大答案:D证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例1证明:任取所以幂函数 在[0,+∞)上是增函数.方法技巧:分子有理化除了作差,还有没有其它方法呢? 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; 证明幂函数 在[0,+∞)上是增函数.(1)作差法:若给出的函数是有根号的式子,往往采用有理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以
