11.2.1.2 直角三角形的性质和判定 课件(22张PPT)
文档属性
| 名称 | 11.2.1.2 直角三角形的性质和判定 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 31.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 18:03:23 | ||
图片预览



文档简介
(共22张PPT)
第11章
三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
11.2.1.2
直角三角形的
性质和判定
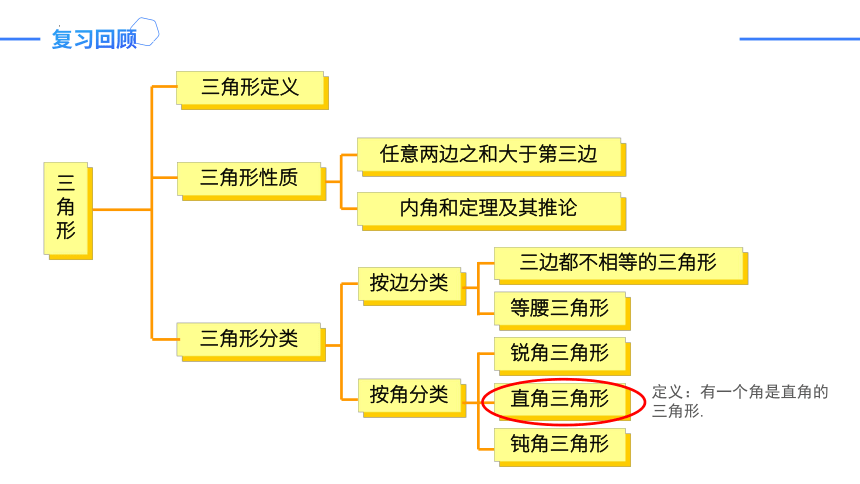
复习回顾
三角形定义
三
角
形
三角形性质
按边分类
按角分类
三角形分类
任意两边之和大于第三边
内角和定理及其推论
锐角三角形
直角三角形
钝角三角形
三边都不相等的三角形
等腰三角形
定义:有一个角是直角的三角形.
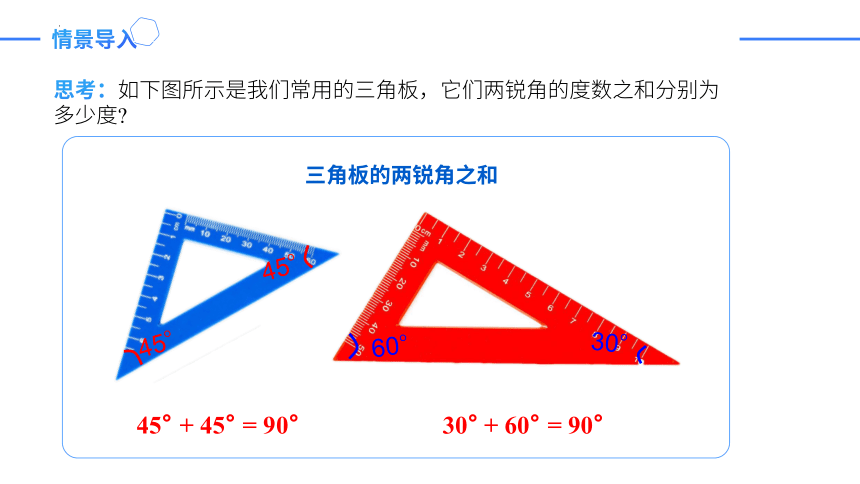
情景导入
思考:如下图所示是我们常用的三角板,它们两锐角的度数之和分别为多少度
三角板的两锐角之和
30°
45°
45°
60°
30° + 60° = 90°
45° + 45° = 90°
新知探究
直角三角形的两锐角之和
思考:如图,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?
A
B
C
解:在Rt△ABC中,∵∠C=90°,
由三角形内角和定理,
可得:∠A+∠B=90°.
由此可得:直角三角形的两个锐角互余.
新知探究
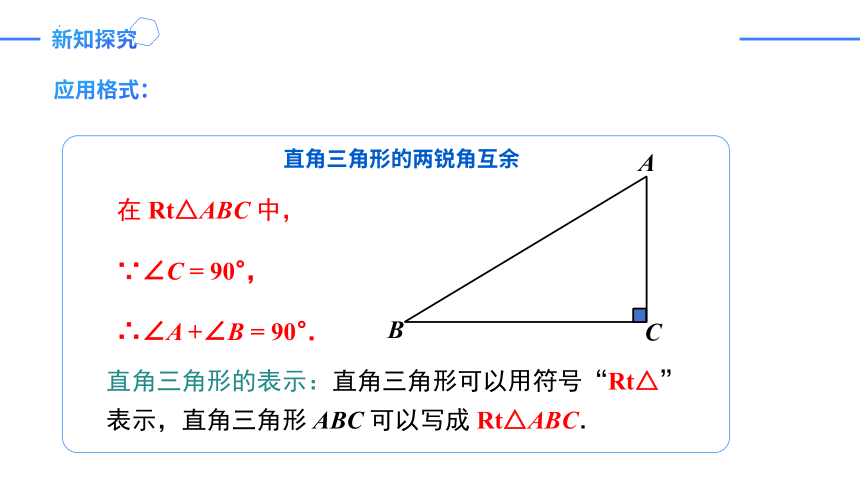
直角三角形的两锐角互余
应用格式:
A
B
C
在 Rt△ABC 中,
∵∠C = 90°,
∴∠A +∠B = 90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形 ABC 可以写成 Rt△ABC.
典例精析
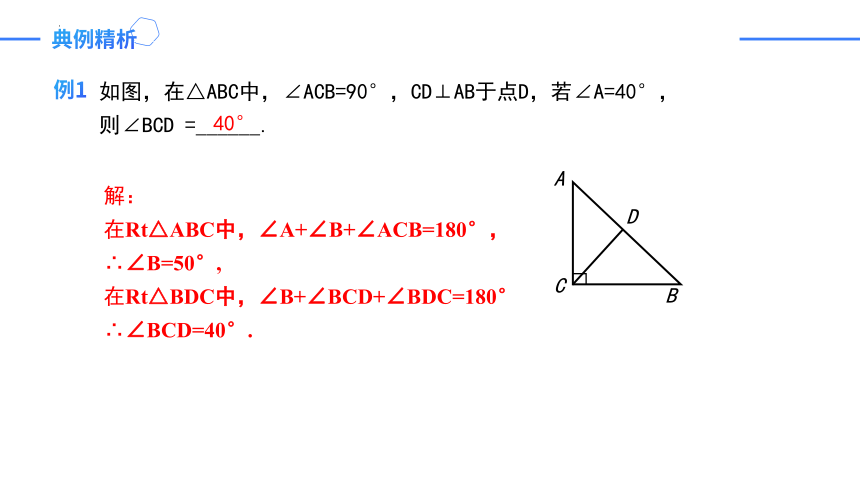
例1
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,
则∠BCD =______.
40°
A
C
D
B
解:
在Rt△ABC中,∠A+∠B+∠ACB=180°,
∴∠B=50°,
在Rt△BDC中,∠B+∠BCD+∠BDC=180°
∴∠BCD=40°.
新知探究
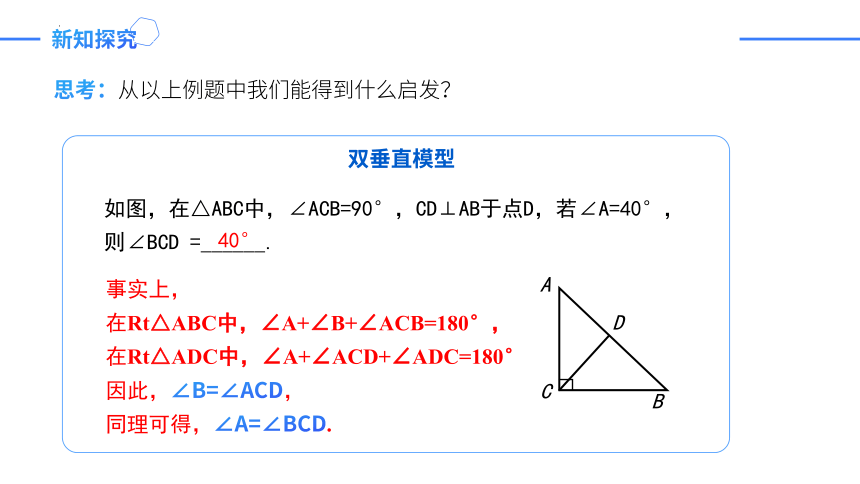
双垂直模型
思考:从以上例题中我们能得到什么启发?
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,
则∠BCD =______.
40°
A
C
D
B
事实上,
在Rt△ABC中,∠A+∠B+∠ACB=180°,
在Rt△ADC中,∠A+∠ACD+∠ADC=180°
因此,∠B=∠ACD,
同理可得,∠A=∠BCD.
典例精析
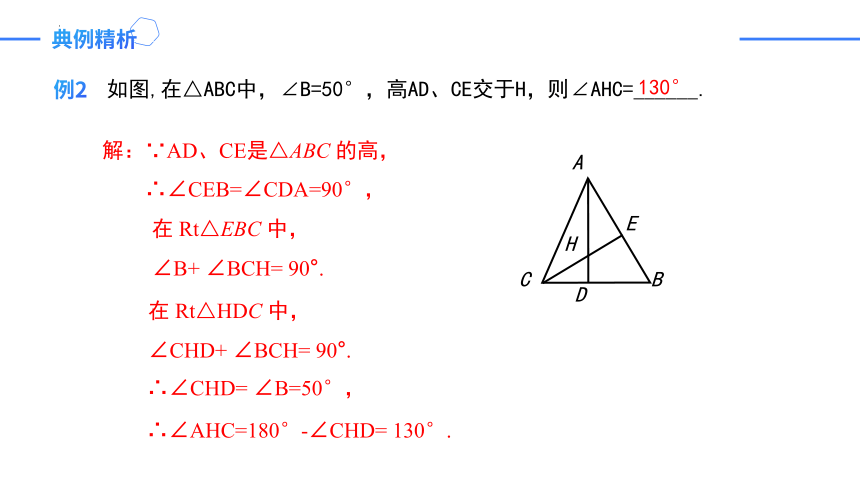
例2
A
C
B
D
H
E
如图,在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC=______.
130°
在 Rt△EBC 中,
∠B+ ∠BCH= 90°.
∴∠CHD= ∠B=50°,
解:∵AD、CE是△ABC 的高,
∴∠CEB=∠CDA=90°,
在 Rt△HDC 中,
∠CHD+ ∠BCH= 90°.
∴∠AHC=180°-∠CHD= 130°.
新知探究
双垂直模型
思考:从以上例题中我们能得到什么启发?
证明:∵ CD⊥AB 于点 D,BE⊥AC 于点 E,
∴∠BEA =∠BDF = 90°.
∴∠ABE +∠A = 90°,
∠ABE +∠DFB = 90°.
∴∠A =∠DFB.
∵∠DFB +∠BFC = 180°,
∴∠A +∠BFC = 180°.
如图,△ABC 中,CD⊥AB 于 D,BE⊥AC于 E,CD,BE 相交于点 F,∠A 与∠BFC 有如下关系:∠A +∠BFC = 180°.
典例精析
例3
如图,∠C =∠D = 90°,AD,BC 相交于点 E. ∠CAE 与 ∠DBE 有什么关系?为什么?
A
B
C
D
E
在 Rt△ACE 中,∠CAE = 90° - ∠AEC.
在 Rt△BDE 中,∠DBE = 90° -∠BED.
∵∠AEC = ∠BED,
∴∠CAE = ∠DBE.
解:∠CAE = ∠DBE. 理由如下:
新知探究
思考:从以上例题中我们能得到什么启发?
新知探究
双垂八字型
事实上,这是一个条件更多的“八字型”.
证明:
∵∠B = ∠D = 90°,
∴∠A +∠AOB = 90°,∠C +∠COD = 90°.
∵∠AOB = ∠COD,
∴∠A = ∠C.
如图,∠B =∠D = 90°,AD 交 BC 于点 O,则∠A =∠C .
O
归纳总结
常见的模型
∠A =∠C
∠A =∠D
O
O
典例精析
例4
如图,在 △ABC 中, ∠A +∠B = 90°, 那么△ABC直角三角形吗?
解:△ABC 是直角三角形,理由如下:
在△ABC 中,因为∠A +∠B +∠C = 180°, 而∠A +∠B = 90°,
所以∠C = 90°,
即△ABC 是直角三角形.
归纳总结
直角三角形的判定
A
B
C
应用格式:
在△ABC 中,
∵∠A +∠B = 90°,
∴△ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
典例精析
例5
如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,那么△AHC是直角三角形吗?为什么?
解:△AHC是直角三角形,理由:
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵AH,CH分别为∠CAB,∠ACD的平分线,
∴∠CAH+∠ACH=90°.
∴∠AHC=90°,即△AHC是直角三角形.
典例精析
例6
如图,∠C = 90°,∠1 = ∠2,△ADE 是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
在 Rt△ABC 中,∠2 + ∠A = 90°.
∵∠1 = ∠2,
∴∠1 + ∠A = 90°,
即 △ADE 是直角三角形.
解:△ADE 是直角三角形. 理由如下:
归纳总结
性质
判定
直角三角形两锐角互余.
有一个角为90°的三角形,叫做直角三角形.
有一个角是直角的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
直角三角形
当堂检测
1. 在一个直角三角形中,有一个锐角等于 40°,则另 一个锐角的度数是( )
A.40° B.50° C.60° D.70°
B
2. 具备下列条件的△ABC 中,不是直角三角形的是 ( )
A.∠A + ∠B = ∠C
B.∠A - ∠B = ∠C
C.∠A∶∠B∶∠C = 1∶2∶3
D.∠A = 2∠B = 3∠C
D
3. 如图所示,△ABC 为直角三角形,∠ACB = 90°,
CD⊥AB,则与∠1 互余的角有( )
A.∠B B.∠A
C.∠BCD 和 ∠A D.∠BCD
C
当堂检测
6. 在△ABC 中,若∠A = 43°,∠B = 47°,则这个三角形是____________.
4. 如图,一张长方形纸片,剪去一角后得到一个三角形,则图中∠1 + ∠2 的度数是______.
90°
5. 如图,AB、CD 相交于点 O,AC⊥CD 于点 C,若∠BOD = 38°,则∠A = _____°.
52
第4题图
第5题图
直角三角形
当堂检测
7.如图,在△ABC中,已知∠B= ∠A= ∠C.求证:△ABC为直角三角形.
证明:∵∠B= ∠A= ∠C,
∴∠A=2∠B,∠C=3∠B.
∵∠A+∠B+∠C=2∠B+∠B+3∠B
=6∠B=180°,
∴∠B=30°,∠A=60°,∠C=90°
∴△ABC为直角三角形.
第11章
三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
11.2.1.2
直角三角形的
性质和判定
复习回顾
三角形定义
三
角
形
三角形性质
按边分类
按角分类
三角形分类
任意两边之和大于第三边
内角和定理及其推论
锐角三角形
直角三角形
钝角三角形
三边都不相等的三角形
等腰三角形
定义:有一个角是直角的三角形.
情景导入
思考:如下图所示是我们常用的三角板,它们两锐角的度数之和分别为多少度
三角板的两锐角之和
30°
45°
45°
60°
30° + 60° = 90°
45° + 45° = 90°
新知探究
直角三角形的两锐角之和
思考:如图,在Rt△ABC中,∠C=90°,两锐角的和等于多少呢?
A
B
C
解:在Rt△ABC中,∵∠C=90°,
由三角形内角和定理,
可得:∠A+∠B=90°.
由此可得:直角三角形的两个锐角互余.
新知探究
直角三角形的两锐角互余
应用格式:
A
B
C
在 Rt△ABC 中,
∵∠C = 90°,
∴∠A +∠B = 90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形 ABC 可以写成 Rt△ABC.
典例精析
例1
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,
则∠BCD =______.
40°
A
C
D
B
解:
在Rt△ABC中,∠A+∠B+∠ACB=180°,
∴∠B=50°,
在Rt△BDC中,∠B+∠BCD+∠BDC=180°
∴∠BCD=40°.
新知探究
双垂直模型
思考:从以上例题中我们能得到什么启发?
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若∠A=40°,
则∠BCD =______.
40°
A
C
D
B
事实上,
在Rt△ABC中,∠A+∠B+∠ACB=180°,
在Rt△ADC中,∠A+∠ACD+∠ADC=180°
因此,∠B=∠ACD,
同理可得,∠A=∠BCD.
典例精析
例2
A
C
B
D
H
E
如图,在△ABC中,∠B=50°,高AD、CE交于H,则∠AHC=______.
130°
在 Rt△EBC 中,
∠B+ ∠BCH= 90°.
∴∠CHD= ∠B=50°,
解:∵AD、CE是△ABC 的高,
∴∠CEB=∠CDA=90°,
在 Rt△HDC 中,
∠CHD+ ∠BCH= 90°.
∴∠AHC=180°-∠CHD= 130°.
新知探究
双垂直模型
思考:从以上例题中我们能得到什么启发?
证明:∵ CD⊥AB 于点 D,BE⊥AC 于点 E,
∴∠BEA =∠BDF = 90°.
∴∠ABE +∠A = 90°,
∠ABE +∠DFB = 90°.
∴∠A =∠DFB.
∵∠DFB +∠BFC = 180°,
∴∠A +∠BFC = 180°.
如图,△ABC 中,CD⊥AB 于 D,BE⊥AC于 E,CD,BE 相交于点 F,∠A 与∠BFC 有如下关系:∠A +∠BFC = 180°.
典例精析
例3
如图,∠C =∠D = 90°,AD,BC 相交于点 E. ∠CAE 与 ∠DBE 有什么关系?为什么?
A
B
C
D
E
在 Rt△ACE 中,∠CAE = 90° - ∠AEC.
在 Rt△BDE 中,∠DBE = 90° -∠BED.
∵∠AEC = ∠BED,
∴∠CAE = ∠DBE.
解:∠CAE = ∠DBE. 理由如下:
新知探究
思考:从以上例题中我们能得到什么启发?
新知探究
双垂八字型
事实上,这是一个条件更多的“八字型”.
证明:
∵∠B = ∠D = 90°,
∴∠A +∠AOB = 90°,∠C +∠COD = 90°.
∵∠AOB = ∠COD,
∴∠A = ∠C.
如图,∠B =∠D = 90°,AD 交 BC 于点 O,则∠A =∠C .
O
归纳总结
常见的模型
∠A =∠C
∠A =∠D
O
O
典例精析
例4
如图,在 △ABC 中, ∠A +∠B = 90°, 那么△ABC直角三角形吗?
解:△ABC 是直角三角形,理由如下:
在△ABC 中,因为∠A +∠B +∠C = 180°, 而∠A +∠B = 90°,
所以∠C = 90°,
即△ABC 是直角三角形.
归纳总结
直角三角形的判定
A
B
C
应用格式:
在△ABC 中,
∵∠A +∠B = 90°,
∴△ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
典例精析
例5
如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,那么△AHC是直角三角形吗?为什么?
解:△AHC是直角三角形,理由:
∵AB∥CD,∴∠CAB+∠ACD=180°.
∵AH,CH分别为∠CAB,∠ACD的平分线,
∴∠CAH+∠ACH=90°.
∴∠AHC=90°,即△AHC是直角三角形.
典例精析
例6
如图,∠C = 90°,∠1 = ∠2,△ADE 是直角三角形吗?为什么?
A
C
B
D
E
(
(
1
2
在 Rt△ABC 中,∠2 + ∠A = 90°.
∵∠1 = ∠2,
∴∠1 + ∠A = 90°,
即 △ADE 是直角三角形.
解:△ADE 是直角三角形. 理由如下:
归纳总结
性质
判定
直角三角形两锐角互余.
有一个角为90°的三角形,叫做直角三角形.
有一个角是直角的三角形是直角三角形.
有两个角互余的三角形是直角三角形.
直角三角形
当堂检测
1. 在一个直角三角形中,有一个锐角等于 40°,则另 一个锐角的度数是( )
A.40° B.50° C.60° D.70°
B
2. 具备下列条件的△ABC 中,不是直角三角形的是 ( )
A.∠A + ∠B = ∠C
B.∠A - ∠B = ∠C
C.∠A∶∠B∶∠C = 1∶2∶3
D.∠A = 2∠B = 3∠C
D
3. 如图所示,△ABC 为直角三角形,∠ACB = 90°,
CD⊥AB,则与∠1 互余的角有( )
A.∠B B.∠A
C.∠BCD 和 ∠A D.∠BCD
C
当堂检测
6. 在△ABC 中,若∠A = 43°,∠B = 47°,则这个三角形是____________.
4. 如图,一张长方形纸片,剪去一角后得到一个三角形,则图中∠1 + ∠2 的度数是______.
90°
5. 如图,AB、CD 相交于点 O,AC⊥CD 于点 C,若∠BOD = 38°,则∠A = _____°.
52
第4题图
第5题图
直角三角形
当堂检测
7.如图,在△ABC中,已知∠B= ∠A= ∠C.求证:△ABC为直角三角形.
证明:∵∠B= ∠A= ∠C,
∴∠A=2∠B,∠C=3∠B.
∵∠A+∠B+∠C=2∠B+∠B+3∠B
=6∠B=180°,
∴∠B=30°,∠A=60°,∠C=90°
∴△ABC为直角三角形.
