22.2 相似与图形面积 课件(38张PPT)
文档属性
| 名称 | 22.2 相似与图形面积 课件(38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 821.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 00:00:00 | ||
图片预览







文档简介
(共38张PPT)
沪科版九年级上册数学
相似与图形面积
利用相似三角形的性质求面积之间的关系
一般地,相似三角形对应线段的比等于相似比.
相似三角形面积的比等于相似比的平方.
相似三角形的性质
相似三角形对应线段的比
相似三角形面积的比
开平方
平方
常见的相似三角形的基本图形:
相似三角形的性质
B
C
D
E
A
“A”型相似
A
B
C
D
E
“X”型相似
若BC//DE,则△ABC ∽△ADE.
若AB//CD,则△ABE ∽△DCE.
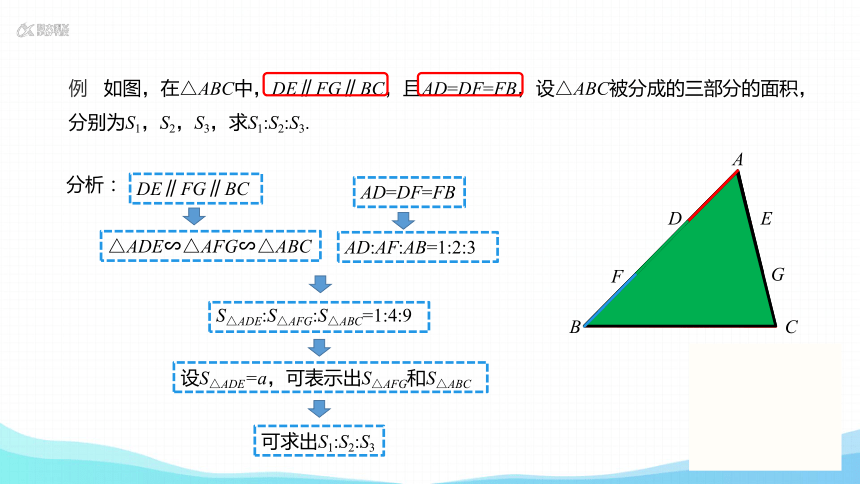
例 如图,在△ABC中,DE∥FG∥BC,且AD=DF=FB,设△ABC被分成的三部分的面积,分别为S1,S2,S3,求S1:S2:S3.
F
G
B
C
A
D
E
S1
S3
S2
分析:
△ADE∽△AFG∽△ABC
DE∥FG∥BC
设S△ADE=a,可表示出S△AFG和S△ABC
AD=DF=FB
AD:AF:AB=1:2:3
S△ADE:S△AFG:S△ABC=1:4:9
可求出S1:S2:S3
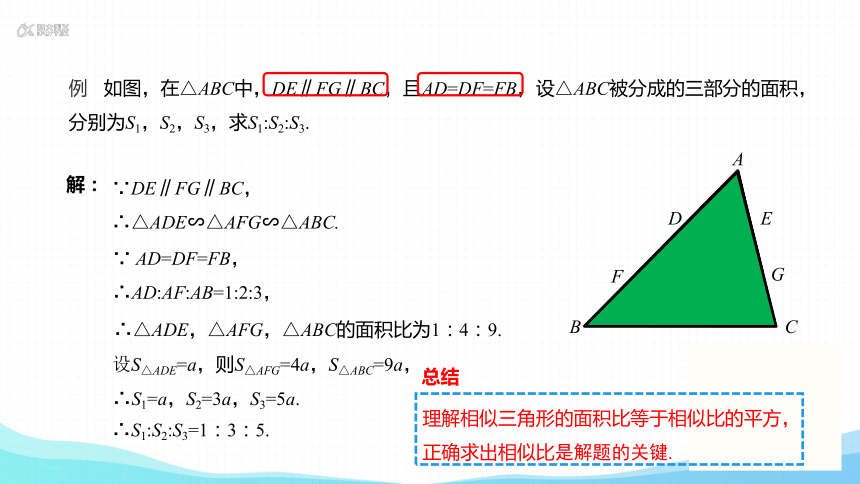
例 如图,在△ABC中,DE∥FG∥BC,且AD=DF=FB,设△ABC被分成的三部分的面积,分别为S1,S2,S3,求S1:S2:S3.
解:
∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC.
F
G
B
C
A
D
E
S3
S2
S1
∵ AD=DF=FB,
∴AD:AF:AB=1:2:3,
设S△ADE=a,则S△AFG=4a,S△ABC=9a,
∴S1:S2:S3=1:3:5.
理解相似三角形的面积比等于相似比的平方,正确求出相似比是解题的关键.
总结
∴△ADE,△AFG,△ABC的面积比为1:4:9.
∴S1=a,S2=3a,S3=5a.
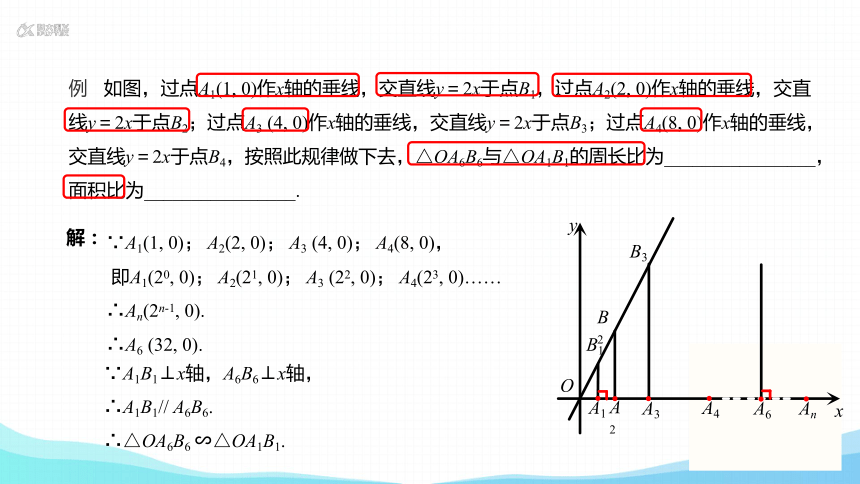
例 如图,过点A1(1, 0)作x轴的垂线,交直线y=2x于点B1,过点A2(2, 0)作x轴的垂线,交直线y=2x于点B2;过点A3 (4, 0)作x轴的垂线,交直线y=2x于点B3;过点A4(8, 0)作x轴的垂线,交直线y=2x于点B4,按照此规律做下去,△OA6B6与△OA1B1的周长比为________________,面积比为________________.
分析:
A1
x
y
A2
A3
O
B1
B2
B3
An(2n-1, 0)
A1(1, 0); A2(2, 0); A3 (4, 0); A4(8, 0)
A6 (32, 0)
通过A1B1⊥x轴,A6B6⊥x轴得A1B1//A6B6,得△OA1B1∽△OA6B6
△OA6B6与△OA1B1的相似比为
可得△OA6B6与△OA1B1的周长比和面积比
A4
An
A6
OA1=1,OA6=32
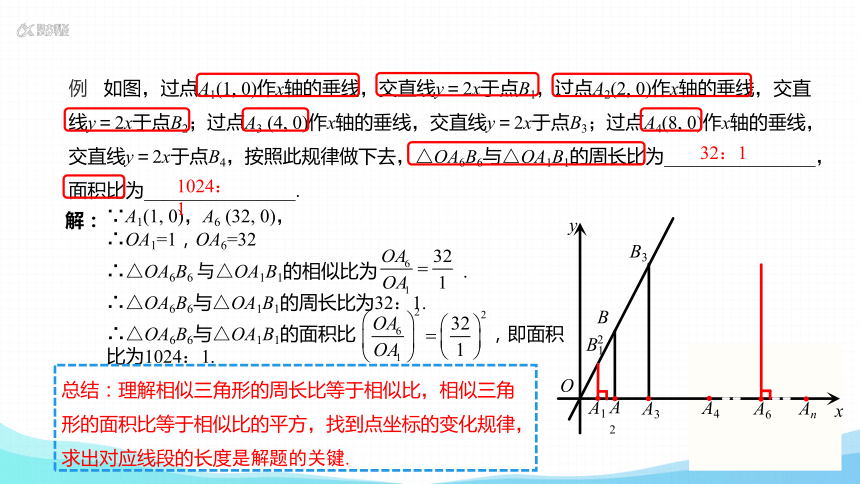
例 如图,过点A1(1, 0)作x轴的垂线,交直线y=2x于点B1,过点A2(2, 0)作x轴的垂线,交直线y=2x于点B2;过点A3 (4, 0)作x轴的垂线,交直线y=2x于点B3;过点A4(8, 0)作x轴的垂线,交直线y=2x于点B4,按照此规律做下去,△OA6B6与△OA1B1的周长比为________________,面积比为________________.
解:
∵A1(1, 0); A2(2, 0); A3 (4, 0); A4(8, 0),
即A1(20, 0); A2(21, 0); A3 (22, 0); A4(23, 0)……
∴An(2n-1, 0).
∴A6 (32, 0).
∵A1B1⊥x轴,A6B6⊥x轴,
∴A1B1// A6B6.
∴△OA6B6 ∽△OA1B1.
A1
x
y
A2
A3
O
B1
B2
B3
A4
An
A6
例 如图,过点A1(1, 0)作x轴的垂线,交直线y=2x于点B1,过点A2(2, 0)作x轴的垂线,交直线y=2x于点B2;过点A3 (4, 0)作x轴的垂线,交直线y=2x于点B3;过点A4(8, 0)作x轴的垂线,交直线y=2x于点B4,按照此规律做下去,△OA6B6与△OA1B1的周长比为________________,面积比为________________.
解:
∵A1(1, 0),A6 (32, 0),
∴OA1=1,OA6=32
∴△OA6B6 与△OA1B1的相似比为 .
∴△OA6B6与△OA1B1的周长比为32:1.
∴△OA6B6与△OA1B1的面积比 ,即面积比为1024:1.
32:1
1024:1
A1
x
y
A2
A3
O
B1
B2
B3
A4
An
A6
总结:理解相似三角形的周长比等于相似比,相似三角形的面积比等于相似比的平方,找到点坐标的变化规律,求出对应线段的长度是解题的关键.
结合底和高之间的关系求面积
常用的求三角形面积的方法
1. 直接求面积:已知底和对应的高,利用公式求面积.
2. 利用相似三角形的性质求面积.
相似三角形对应线段的比
相似三角形面积的比
开平方
平方
常用的求三角形面积的方法
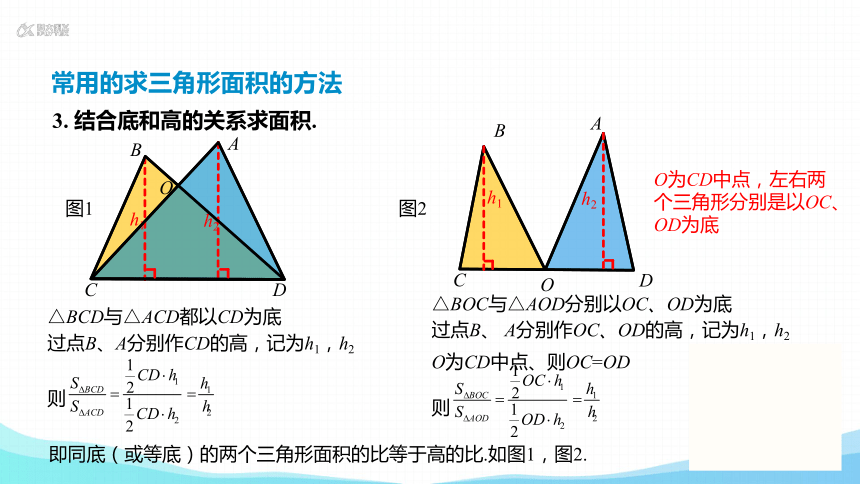
3. 结合底和高的关系求面积.
B
C
D
O
A
△BCD与△ACD都以CD为底
△BOC与△AOD分别以OC、OD为底
O为CD中点,左右两个三角形分别是以OC、OD为底
h1
h2
过点B、A分别作CD的高,记为h1,h2
则
h2
过点B、 A分别作OC、OD的高,记为h1,h2
B
C
D
O
A
h1
O为CD中点、则OC=OD
则
即同底(或等底)的两个三角形面积的比等于高的比.如图1,图2.
图1
图2
过点A作CD的高,记为h
常用的求三角形面积的方法
3. 结合底和高的关系求面积.
C
D
A
B
B
C
D
A
△ABD与△ACD分别以BD、CD为底
h
则
O
h2
h1
△BOC与△ACD分别以CO、CD为底且高相等
过点B、 A分作CO、CD的高,分别为h1,h2,则h1=h2
则
即同高(或等高)的两个三角形面积的比等于底边的比.如图1,图2.
图1
图2
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
A
B
C
D
E
O
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
A
B
C
D
E
O
分析:
□ABCD中,E是CD的中点
△AOB∽△EOD,且相似比为2:1
△AOB的面积为4,AO:EO=2:1
1
4
由△AOD与△EOD同高,可得它们面积比为AO:EO=2:1
△AOD的面积为2,□ABCD的面积为12
可求出四边形BOEC的面积
2
△DOE的面积是1
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
解:
∵□ABCD中,E是CD的中点,
∴△AOB∽△EOD,且相似比为2:1.
∴△AOB与△EOD的面积比为4:1, AO:EO=2:1
∵S△DOE=1,
∴S△AOB=4.
A
B
C
D
E
O
1
4
∵△AOD与△EOD同高,
∴△AOD与△EOD的面积比为AO:EO=2:1.
∴S△AOD=2.
2
∴S△ABD=6.
∴S□ABCD=2S△ABD=12.
∴四边形BOEC的面积为
S□ABCD-S△ABD-S△DOE
=12-6-1=5.
5
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
A
B
C
D
E
O
分析:
△AOB∽△EOD,且相似比为3:1
△AOB的面积为9,AO:EO=3:1
□ABCD中,
9
由△AOD与△EOD同高,可得它们面积比为AO:EO=3:1
△AOD的面积为3,□ABCD的面积为24
可求出四边形BOEC的面积
3
1
△DOE的面积是1
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
解:
∵S△DOE=1,
∴S△AOB=9.
∵□ABCD中, ,
∴△AOB∽△EOD,且相似比为3:1.
∴△AOB与△EOD的面积比为9:1, AO:EO=3:1
A
B
C
D
E
O
9
∵△AOD与△EOD同高,
∴△AOD与△EOD的面积比为AO:EO=3:1.
∴S△AOD=3.
3
1
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
A
B
C
D
E
O
∴S△ABD=12.
∴S□ABCD=2S△ABD=24.
∴四边形BOEC的面积为
S□ABCD-S△ABD-S△DOE
=24-12-1=11.
解:
1
3
9
理解相似三角形的面积比等于相似比的平方,识别出同高的两个三角形,并利用其面积比等于对应的底边之比是解题的关键.
总结
11
例 如图,在△ABC中,D、E分别是AB、AC上的点,且DE//AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD为( )
A. 1:16 B. 1:18 C. 1:20 D. 1:24
B
C
D
E
A
分析:
△BDE∽△BAC
DE//AC
S△BDE:S△CDE=1:4,△BDE与△CDE同高
可求出△BDE与△BAC的面积比1:25
可求出S△BDE:S△ACD
BE:EC=1:4
BE:BC=1:5
1
4
1
4
5
1
例 如图,在△ABC中,D、E分别是AB、AC上的点,且DE//AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD为( )
A. 1:16 B. 1:18 C. 1:20 D. 1:24
解:
∵DE//AC,
∴△BDE∽△BAC.
B
C
D
E
A
∵S△BDE:S△CDE=1:4,△BDE与△CDE同高,
∴BE:EC=1:4.
∴BE:BC=1:5.
∴S△BDE:S△BAC=1:25.
1
4
1
4
5
1
例 如图,在△ABC中,D、E分别是AB、AC上的点,且DE//AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD为( )
A. 1:16 B. 1:18 C. 1:20 D. 1:24
解:
设S△BDE=a,则S△CDE=4a,S△BAC=25a,
∴S△ACD=20a.
∴S△BDE:S△ACD=1:20.
故选 C.
C
B
C
D
E
A
a
4a
20a
理解相似三角形的面积比等于相似比的平方,识别出同高的两个三角形,并利用其面积比等于对应的底边之比是解题的关键.
总结
例 如图 ,△ABC 与△DEC 重叠的情形,其中 E 在 BC 上,AC 交 DE 于 F 点,且 AB//DE.若△ABC 与△DEC的面积相等, 且 EF = 9,AB = 12,则 DF 的长度为( )
A. 3 B. 7 C. 16 D. 15
A
C
B
F
D
E
分析:
求出
△CEF∽△CBA
AB//DE
求出
求出
求出 的长度
由△CEF,△DFC同高求出
例 如图 ,△ABC 与△DEC 重叠的情形,其中 E 在 BC 上,AC 交 DE 于 F 点,且 AB//DE.若△ABC 与△DEC的面积相等, 且 EF = 9,AB = 12,则 DF 的长度为( )
A. 3 B. 7 C. 16 D. 15
解:
∵EF//AB,
∴△CEF∽△CBA.
∵S△ABC=S△DEC.
∴ .
∴ .
∴ .
A
C
B
F
D
E
例 如图 ,△ABC 与△DEC 重叠的情形,其中 E 在 BC 上,AC 交 DE 于 F 点,且 AB//DE.若△ABC 与△DEC的面积相等, 且 EF = 9,AB = 12,则 DF 的长度为( )
A. 3 B. 7 C. 16 D. 15
A
C
B
F
D
E
解:
∵△CEF 与△DFC 的高相同,
∵EF = 9,
∴ .
∴DF = 7.
故选:B.
B
9
7
理解相似三角形的面积比等于相似比的平方,识别出同高的两个三角形,并利用其面积比等于对应的底边之比是解题的关键.
总结
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
A
C
B
D
E
F
图①
C
B
A
F
G
E
D
图②
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
分析:
∠CFE= ∠A
EF//AB
A
C
B
D
E
F
图①
DF//BC
∠DFA= ∠C
△ADF∽△FEC
由面积比可得出相似比
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
解:
∵EF//AB,
∴∠CFE= ∠A.
图①
∵DF//BC,
∴∠DFA= ∠C.
∵△ADF,△EFC的面积分别为3,1, ,
∴△ADF∽△FEC.
A
C
B
D
E
F
∴ .
3
1
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
A
C
B
D
E
F
图①
分析:
△CEF∽△CBA
EF//AB
DF//BC
△FAD∽△CAB
可分别求出S1,S2与S△ABC的关系
S=S△ABC-S1-S2
计算 可得结果
S1
S2
S
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
图①
解:
∵EF//AB,DF//BC,
∴△CEF∽△CBA,△FAD∽△CAB,且四边形DBEF是平行四边形.
∴EF=BD=b
设AD=a,BD=b,
A
C
B
D
E
F
b
a
∴ ,
.
S1
S2
b
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
A
C
B
D
E
F
图①
解:
∴
.
S
S1
S2
a
b
∴ ,
.
b
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
解:
A
C
B
D
E
F
图①
S
S1
S2
a
b
∴
∴ .
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
C
B
A
F
G
E
D
图②
分析:
DE//BC,DF//EG
四边形DEGF是平行四边形
DF=EG
可将△EGC平移到使边EG、DF重合,拼接成新△BDH
H
通过△ADE与△BDH之间的面积关系求出AD:AB,即可求出△ABC的面积
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
解:
∵DE//BC,DF//EG,
∴四边形DEGF是平行四边形.
∴ DF=EG.
C
B
A
F
G
E
D
图②
H
将△EGC平移到使边EG、DF重合,拼接成新三角形,记为△BDH,则
△BDH∽△DAE∽△BAC,
S△BDH=S△BDF+S△CEG=7+5=12.
12
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
解:
∵△BDH∽△DAE,
∴S△BDH:S△DAE=12:3=4:1.
∴BD:AD=2:1.
∴AB:AD=3:1.
C
B
A
F
G
E
D
图②
H
∵△BAC∽△DAE,
∴S△BAC:S△DAE=9:1.
3
12
∵S△DAE=3,
∴S△BAC=27.
27
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
根据相似三角形对应线段的比等于相似比,相似三角形的面积比等于相似比的平方可求出两个相似三角形的对应高之比;
通过设未知数,表示出S1,S2,S的值,体会用代数方法解决几何问题的思路;
解题过程中可以将图形通过拼接等方式,构造新的三角形,利用相似三角形的面积比等于相似比的平方,求出△ABC的面积.
总结
相似与图
形面积
运用相似三角形的性质求面积之间的关系
相似三角形对应线段的比等于相似比
相似三角形面积的比等于相似比的平方
结合底和高的关系求面积
相似三角形对应线段的比
相似三角形面积的比
开平方
平方
已知底和高直接求面积
高和对应的底相同或相等
两三角形面积相等
等底(同底)
两三角形面积之比等于对应的高之比
等高(同高)
两三角形面积之比等于对应的底之比
再 见
沪科版九年级上册数学
相似与图形面积
利用相似三角形的性质求面积之间的关系
一般地,相似三角形对应线段的比等于相似比.
相似三角形面积的比等于相似比的平方.
相似三角形的性质
相似三角形对应线段的比
相似三角形面积的比
开平方
平方
常见的相似三角形的基本图形:
相似三角形的性质
B
C
D
E
A
“A”型相似
A
B
C
D
E
“X”型相似
若BC//DE,则△ABC ∽△ADE.
若AB//CD,则△ABE ∽△DCE.
例 如图,在△ABC中,DE∥FG∥BC,且AD=DF=FB,设△ABC被分成的三部分的面积,分别为S1,S2,S3,求S1:S2:S3.
F
G
B
C
A
D
E
S1
S3
S2
分析:
△ADE∽△AFG∽△ABC
DE∥FG∥BC
设S△ADE=a,可表示出S△AFG和S△ABC
AD=DF=FB
AD:AF:AB=1:2:3
S△ADE:S△AFG:S△ABC=1:4:9
可求出S1:S2:S3
例 如图,在△ABC中,DE∥FG∥BC,且AD=DF=FB,设△ABC被分成的三部分的面积,分别为S1,S2,S3,求S1:S2:S3.
解:
∵DE∥FG∥BC,
∴△ADE∽△AFG∽△ABC.
F
G
B
C
A
D
E
S3
S2
S1
∵ AD=DF=FB,
∴AD:AF:AB=1:2:3,
设S△ADE=a,则S△AFG=4a,S△ABC=9a,
∴S1:S2:S3=1:3:5.
理解相似三角形的面积比等于相似比的平方,正确求出相似比是解题的关键.
总结
∴△ADE,△AFG,△ABC的面积比为1:4:9.
∴S1=a,S2=3a,S3=5a.
例 如图,过点A1(1, 0)作x轴的垂线,交直线y=2x于点B1,过点A2(2, 0)作x轴的垂线,交直线y=2x于点B2;过点A3 (4, 0)作x轴的垂线,交直线y=2x于点B3;过点A4(8, 0)作x轴的垂线,交直线y=2x于点B4,按照此规律做下去,△OA6B6与△OA1B1的周长比为________________,面积比为________________.
分析:
A1
x
y
A2
A3
O
B1
B2
B3
An(2n-1, 0)
A1(1, 0); A2(2, 0); A3 (4, 0); A4(8, 0)
A6 (32, 0)
通过A1B1⊥x轴,A6B6⊥x轴得A1B1//A6B6,得△OA1B1∽△OA6B6
△OA6B6与△OA1B1的相似比为
可得△OA6B6与△OA1B1的周长比和面积比
A4
An
A6
OA1=1,OA6=32
例 如图,过点A1(1, 0)作x轴的垂线,交直线y=2x于点B1,过点A2(2, 0)作x轴的垂线,交直线y=2x于点B2;过点A3 (4, 0)作x轴的垂线,交直线y=2x于点B3;过点A4(8, 0)作x轴的垂线,交直线y=2x于点B4,按照此规律做下去,△OA6B6与△OA1B1的周长比为________________,面积比为________________.
解:
∵A1(1, 0); A2(2, 0); A3 (4, 0); A4(8, 0),
即A1(20, 0); A2(21, 0); A3 (22, 0); A4(23, 0)……
∴An(2n-1, 0).
∴A6 (32, 0).
∵A1B1⊥x轴,A6B6⊥x轴,
∴A1B1// A6B6.
∴△OA6B6 ∽△OA1B1.
A1
x
y
A2
A3
O
B1
B2
B3
A4
An
A6
例 如图,过点A1(1, 0)作x轴的垂线,交直线y=2x于点B1,过点A2(2, 0)作x轴的垂线,交直线y=2x于点B2;过点A3 (4, 0)作x轴的垂线,交直线y=2x于点B3;过点A4(8, 0)作x轴的垂线,交直线y=2x于点B4,按照此规律做下去,△OA6B6与△OA1B1的周长比为________________,面积比为________________.
解:
∵A1(1, 0),A6 (32, 0),
∴OA1=1,OA6=32
∴△OA6B6 与△OA1B1的相似比为 .
∴△OA6B6与△OA1B1的周长比为32:1.
∴△OA6B6与△OA1B1的面积比 ,即面积比为1024:1.
32:1
1024:1
A1
x
y
A2
A3
O
B1
B2
B3
A4
An
A6
总结:理解相似三角形的周长比等于相似比,相似三角形的面积比等于相似比的平方,找到点坐标的变化规律,求出对应线段的长度是解题的关键.
结合底和高之间的关系求面积
常用的求三角形面积的方法
1. 直接求面积:已知底和对应的高,利用公式求面积.
2. 利用相似三角形的性质求面积.
相似三角形对应线段的比
相似三角形面积的比
开平方
平方
常用的求三角形面积的方法
3. 结合底和高的关系求面积.
B
C
D
O
A
△BCD与△ACD都以CD为底
△BOC与△AOD分别以OC、OD为底
O为CD中点,左右两个三角形分别是以OC、OD为底
h1
h2
过点B、A分别作CD的高,记为h1,h2
则
h2
过点B、 A分别作OC、OD的高,记为h1,h2
B
C
D
O
A
h1
O为CD中点、则OC=OD
则
即同底(或等底)的两个三角形面积的比等于高的比.如图1,图2.
图1
图2
过点A作CD的高,记为h
常用的求三角形面积的方法
3. 结合底和高的关系求面积.
C
D
A
B
B
C
D
A
△ABD与△ACD分别以BD、CD为底
h
则
O
h2
h1
△BOC与△ACD分别以CO、CD为底且高相等
过点B、 A分作CO、CD的高,分别为h1,h2,则h1=h2
则
即同高(或等高)的两个三角形面积的比等于底边的比.如图1,图2.
图1
图2
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
A
B
C
D
E
O
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
A
B
C
D
E
O
分析:
□ABCD中,E是CD的中点
△AOB∽△EOD,且相似比为2:1
△AOB的面积为4,AO:EO=2:1
1
4
由△AOD与△EOD同高,可得它们面积比为AO:EO=2:1
△AOD的面积为2,□ABCD的面积为12
可求出四边形BOEC的面积
2
△DOE的面积是1
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
解:
∵□ABCD中,E是CD的中点,
∴△AOB∽△EOD,且相似比为2:1.
∴△AOB与△EOD的面积比为4:1, AO:EO=2:1
∵S△DOE=1,
∴S△AOB=4.
A
B
C
D
E
O
1
4
∵△AOD与△EOD同高,
∴△AOD与△EOD的面积比为AO:EO=2:1.
∴S△AOD=2.
2
∴S△ABD=6.
∴S□ABCD=2S△ABD=12.
∴四边形BOEC的面积为
S□ABCD-S△ABD-S△DOE
=12-6-1=5.
5
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
A
B
C
D
E
O
分析:
△AOB∽△EOD,且相似比为3:1
△AOB的面积为9,AO:EO=3:1
□ABCD中,
9
由△AOD与△EOD同高,可得它们面积比为AO:EO=3:1
△AOD的面积为3,□ABCD的面积为24
可求出四边形BOEC的面积
3
1
△DOE的面积是1
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
解:
∵S△DOE=1,
∴S△AOB=9.
∵□ABCD中, ,
∴△AOB∽△EOD,且相似比为3:1.
∴△AOB与△EOD的面积比为9:1, AO:EO=3:1
A
B
C
D
E
O
9
∵△AOD与△EOD同高,
∴△AOD与△EOD的面积比为AO:EO=3:1.
∴S△AOD=3.
3
1
例 如图,□ABCD中,E是CD的中点,AE,BD交于点O.△DOE的面积是1.
(1)求四边形BOEC的面积.
(2)若 ,求此时四边形BOEC的面积.
A
B
C
D
E
O
∴S△ABD=12.
∴S□ABCD=2S△ABD=24.
∴四边形BOEC的面积为
S□ABCD-S△ABD-S△DOE
=24-12-1=11.
解:
1
3
9
理解相似三角形的面积比等于相似比的平方,识别出同高的两个三角形,并利用其面积比等于对应的底边之比是解题的关键.
总结
11
例 如图,在△ABC中,D、E分别是AB、AC上的点,且DE//AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD为( )
A. 1:16 B. 1:18 C. 1:20 D. 1:24
B
C
D
E
A
分析:
△BDE∽△BAC
DE//AC
S△BDE:S△CDE=1:4,△BDE与△CDE同高
可求出△BDE与△BAC的面积比1:25
可求出S△BDE:S△ACD
BE:EC=1:4
BE:BC=1:5
1
4
1
4
5
1
例 如图,在△ABC中,D、E分别是AB、AC上的点,且DE//AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD为( )
A. 1:16 B. 1:18 C. 1:20 D. 1:24
解:
∵DE//AC,
∴△BDE∽△BAC.
B
C
D
E
A
∵S△BDE:S△CDE=1:4,△BDE与△CDE同高,
∴BE:EC=1:4.
∴BE:BC=1:5.
∴S△BDE:S△BAC=1:25.
1
4
1
4
5
1
例 如图,在△ABC中,D、E分别是AB、AC上的点,且DE//AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD为( )
A. 1:16 B. 1:18 C. 1:20 D. 1:24
解:
设S△BDE=a,则S△CDE=4a,S△BAC=25a,
∴S△ACD=20a.
∴S△BDE:S△ACD=1:20.
故选 C.
C
B
C
D
E
A
a
4a
20a
理解相似三角形的面积比等于相似比的平方,识别出同高的两个三角形,并利用其面积比等于对应的底边之比是解题的关键.
总结
例 如图 ,△ABC 与△DEC 重叠的情形,其中 E 在 BC 上,AC 交 DE 于 F 点,且 AB//DE.若△ABC 与△DEC的面积相等, 且 EF = 9,AB = 12,则 DF 的长度为( )
A. 3 B. 7 C. 16 D. 15
A
C
B
F
D
E
分析:
求出
△CEF∽△CBA
AB//DE
求出
求出
求出 的长度
由△CEF,△DFC同高求出
例 如图 ,△ABC 与△DEC 重叠的情形,其中 E 在 BC 上,AC 交 DE 于 F 点,且 AB//DE.若△ABC 与△DEC的面积相等, 且 EF = 9,AB = 12,则 DF 的长度为( )
A. 3 B. 7 C. 16 D. 15
解:
∵EF//AB,
∴△CEF∽△CBA.
∵S△ABC=S△DEC.
∴ .
∴ .
∴ .
A
C
B
F
D
E
例 如图 ,△ABC 与△DEC 重叠的情形,其中 E 在 BC 上,AC 交 DE 于 F 点,且 AB//DE.若△ABC 与△DEC的面积相等, 且 EF = 9,AB = 12,则 DF 的长度为( )
A. 3 B. 7 C. 16 D. 15
A
C
B
F
D
E
解:
∵△CEF 与△DFC 的高相同,
∵EF = 9,
∴ .
∴DF = 7.
故选:B.
B
9
7
理解相似三角形的面积比等于相似比的平方,识别出同高的两个三角形,并利用其面积比等于对应的底边之比是解题的关键.
总结
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
A
C
B
D
E
F
图①
C
B
A
F
G
E
D
图②
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
分析:
∠CFE= ∠A
EF//AB
A
C
B
D
E
F
图①
DF//BC
∠DFA= ∠C
△ADF∽△FEC
由面积比可得出相似比
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
解:
∵EF//AB,
∴∠CFE= ∠A.
图①
∵DF//BC,
∴∠DFA= ∠C.
∵△ADF,△EFC的面积分别为3,1, ,
∴△ADF∽△FEC.
A
C
B
D
E
F
∴ .
3
1
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
A
C
B
D
E
F
图①
分析:
△CEF∽△CBA
EF//AB
DF//BC
△FAD∽△CAB
可分别求出S1,S2与S△ABC的关系
S=S△ABC-S1-S2
计算 可得结果
S1
S2
S
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
图①
解:
∵EF//AB,DF//BC,
∴△CEF∽△CBA,△FAD∽△CAB,且四边形DBEF是平行四边形.
∴EF=BD=b
设AD=a,BD=b,
A
C
B
D
E
F
b
a
∴ ,
.
S1
S2
b
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
A
C
B
D
E
F
图①
解:
∴
.
S
S1
S2
a
b
∴ ,
.
b
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
解:
A
C
B
D
E
F
图①
S
S1
S2
a
b
∴
∴ .
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
C
B
A
F
G
E
D
图②
分析:
DE//BC,DF//EG
四边形DEGF是平行四边形
DF=EG
可将△EGC平移到使边EG、DF重合,拼接成新△BDH
H
通过△ADE与△BDH之间的面积关系求出AD:AB,即可求出△ABC的面积
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
解:
∵DE//BC,DF//EG,
∴四边形DEGF是平行四边形.
∴ DF=EG.
C
B
A
F
G
E
D
图②
H
将△EGC平移到使边EG、DF重合,拼接成新三角形,记为△BDH,则
△BDH∽△DAE∽△BAC,
S△BDH=S△BDF+S△CEG=7+5=12.
12
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
解:
∵△BDH∽△DAE,
∴S△BDH:S△DAE=12:3=4:1.
∴BD:AD=2:1.
∴AB:AD=3:1.
C
B
A
F
G
E
D
图②
H
∵△BAC∽△DAE,
∴S△BAC:S△DAE=9:1.
3
12
∵S△DAE=3,
∴S△BAC=27.
27
例 如图①,在△ABC中,点D,E,F分别在AB,BC,AC上,且DF//BC,EF//AB.
设△ADF的边DF上的高为h1,设△EFC的边CE上的高为h2.
(1)若△ADF、△EFC的面积分别为3,1,则 =__________;
(2)设△ADF、△EFC、四边形BDFE的面积分别为S1,S2,S,求证: ;
(3)如图②,在△ABC中,点D,E分别在AB、AC上,点F,G在BC上,且DE//BC,DF//EG. 若△ADE、△DBF、△EGC的面积分别为3,7,5,求△ABC的面积.
根据相似三角形对应线段的比等于相似比,相似三角形的面积比等于相似比的平方可求出两个相似三角形的对应高之比;
通过设未知数,表示出S1,S2,S的值,体会用代数方法解决几何问题的思路;
解题过程中可以将图形通过拼接等方式,构造新的三角形,利用相似三角形的面积比等于相似比的平方,求出△ABC的面积.
总结
相似与图
形面积
运用相似三角形的性质求面积之间的关系
相似三角形对应线段的比等于相似比
相似三角形面积的比等于相似比的平方
结合底和高的关系求面积
相似三角形对应线段的比
相似三角形面积的比
开平方
平方
已知底和高直接求面积
高和对应的底相同或相等
两三角形面积相等
等底(同底)
两三角形面积之比等于对应的高之比
等高(同高)
两三角形面积之比等于对应的底之比
再 见
