22.相似的综合应用 课件(34张PPT)
文档属性
| 名称 | 22.相似的综合应用 课件(34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 848.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 17:57:31 | ||
图片预览







文档简介
(共34张PPT)
沪科版九年级上册数学
相似的综合应用
相似的综合应用
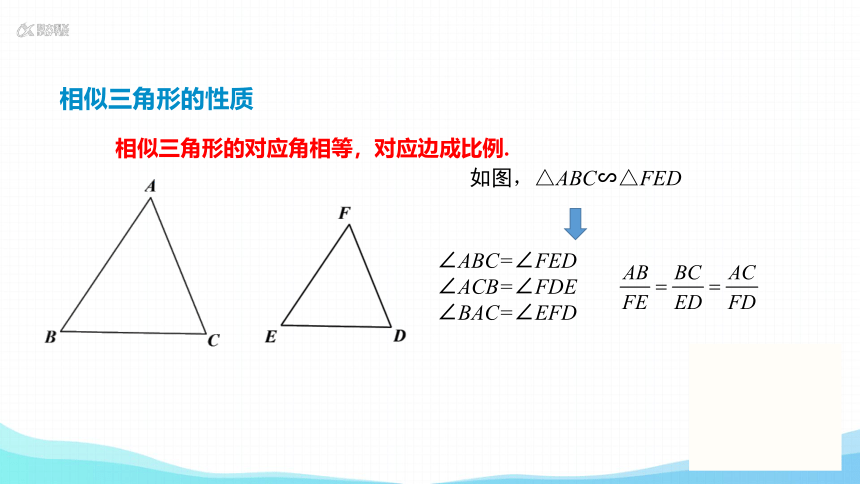
相似三角形的对应角相等,对应边成比例.
相似三角形的性质
如图,△ABC∽△FED
∠ABC=∠FED
∠ACB=∠FDE
∠BAC=∠EFD
相似三角形的性质
如图,若△ABC∽△FED,相似比为k.
AG,FH分别是两个三角形的高线;
AK,FJ分别是两个三角形的中线;
BM,EN分别是两个三角形对应角的角平分线.
相似三角形对应线段的比等于相似比.
相似三角形周长的比等于相似比.
相似三角形面积的比等于相似比的平方.
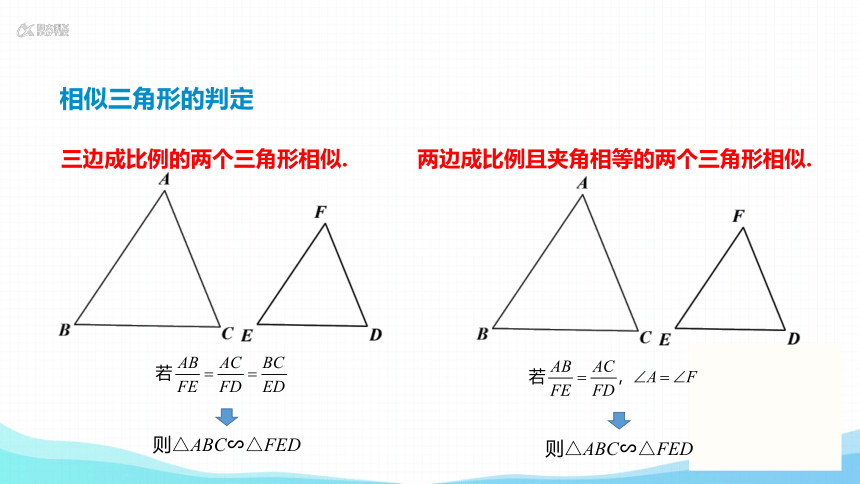
相似三角形的判定
若DE//BC,
则△ADE∽△ABC.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
“A”型
“X”型
若AB//CD,
则△ABO∽△DCO.
相似三角形的判定
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
则△ABC∽△FED
则△ABC∽△FED
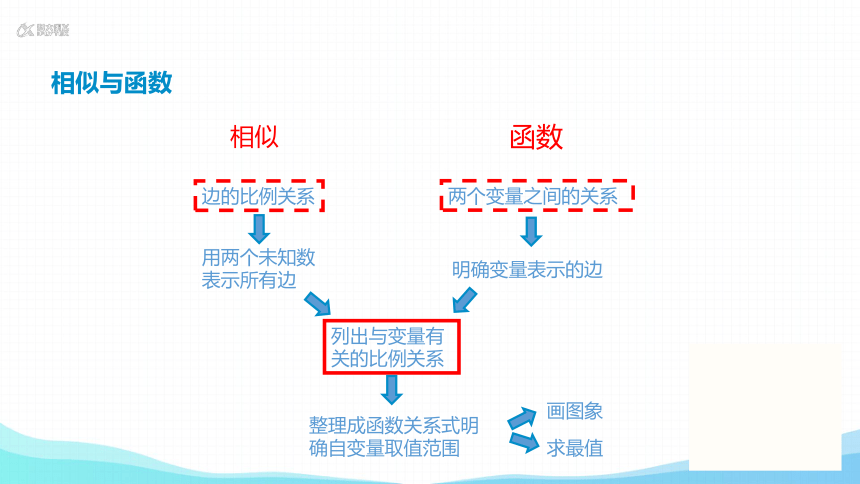
相似与函数
相似
函数
边的比例关系
两个变量之间的关系
明确变量表示的边
用两个未知数表示所有边
列出与变量有关的比例关系
整理成函数关系式明确自变量取值范围
画图象
求最值
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小
当a>0时,x的值离对称轴x=h越近,y的值越小;
当a<0时,x的值离对称轴x=h越近,y的值越大
利用函数求最值
一次函数最值
二次函数最值
三角形相似
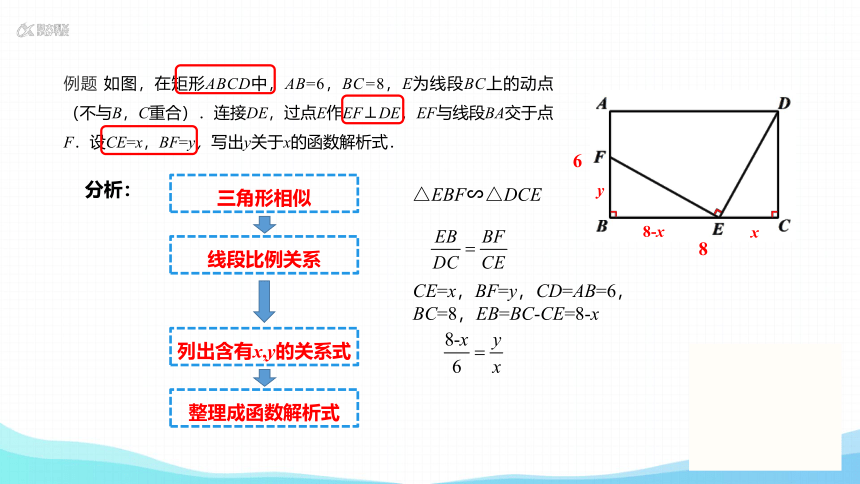
例题 如图,在矩形ABCD中,AB=6,BC=8,E为线段BC上的动点(不与B,C重合).连接DE,过点E作EF⊥DE,EF与线段BA交于点F.设CE=x,BF=y,写出y关于x的函数解析式.
分析:
线段比例关系
△EBF∽△DCE
8
6
列出含有x,y的关系式
整理成函数解析式
x
y
8-x
CE=x,BF=y,CD=AB=6,BC=8,EB=BC-CE=8-x
在矩形ABCD中, ∠B=∠C=90 ,
例题 如图,在矩形ABCD中,AB=6,BC=8,E为线段BC上的动点(不与B,C重合).连接DE,过点E作EF⊥DE,EF与线段BA交于点F.设CE=x,BF=y,写出y关于x的函数解析式.
解:
6
8
小结:相似三角形有关知识与函数相结合时,一般通过相似三角形对应边成比例得到比例式,从而建立两个变量之间的关系.
∴∠BEF+∠DEC=90°
∵CE=x,BF=y,CD=AB=6,BC=8,
x
y
8-x
∴EB=BC-CE=8-x
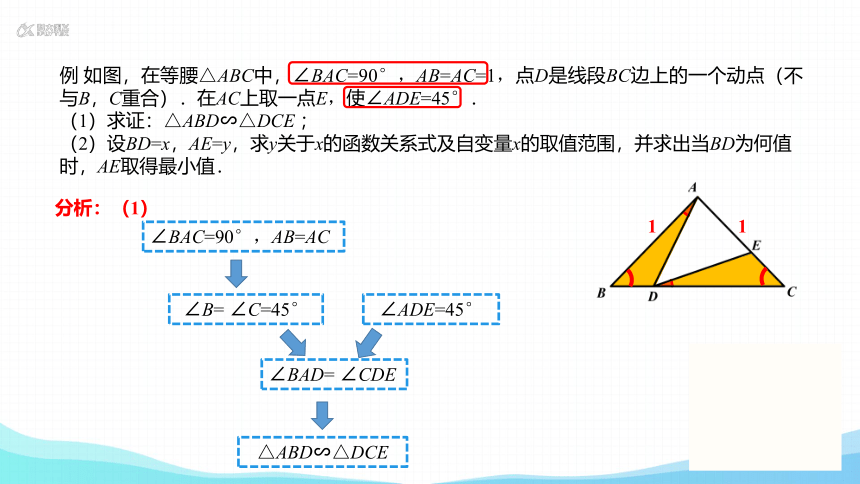
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABD∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
分析:(1)
1
1
∠BAC=90°,AB=AC
∠BAD= ∠CDE
△ABD∽△DCE
∠B= ∠C=45°
∠ADE=45°
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABC∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
证明:(1)
∵△ABC是等腰三角形, ∠BAC=90°
∴∠B= ∠C =45°
在△ABD中,∠ADB+∠BAD+∠B=180°
∴∠ADB+ ∠BAD=135°
又∵∠ADB+∠EDC +∠ADE=180°且∠ADE=45°
∴∠ADB+ ∠EDC=135°
∴ ∠BAD= ∠CDE
∴ △ABD∽△DCE
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABC∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
分析:(2)
1
1-y
BC=
△ABD∽△DCE
x
y
∠BAC=90°,AB=AC=1
DC= -x
CE=1-y
化为二次函数求最值
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABC∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
解:(2)
小结:将几何问题中两条线段关系表达成了一个二次函数的关系,研究线段的最小值问题,就转化到了研究二次函数的最值问题.
∵∠BAC=90°, AB=AC=1
∴BC =
∵ BD=x,AE=y
∴CD= , CE=
当 即BD= 时,
y有最小值.
∴
∴
∴
∴
∴
又∵ △ABD∽△DCE
(01
1-y
x
y
1
图②
例题 如图①,有一块三角形余料ABC.它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
问题:(1)加工成的正方形零件的边长为多少?
(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件两条相邻的边长就不能确定,但这个矩形面积有最大值,求面积达到这个最大值时矩形零件相邻的两条边长.
图①
图①
分析:
△APN∽△ABC
PN
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
问题:(1)加工成的正方形零件的边长为多少?
解:设正方形的边长为xmm,则PN=PQ=ED=x.
∵BC=120 ,AD=80,
∴AE=AD-ED=80-x.
∵ PN∥BC,
∴△APN∽△ABC.
∴ ,
∴ ,即 .
得x=48.
所以,正方形零件的边长为48 mm.
图①
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
问题:(1)加工成的正方形零件的边长为多少?
图②
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件两条相邻的边长就不能确定,但这个矩形面积有最大值,求面积达到这个最大值时矩形零件相邻的两条边长.
分析:
△APN∽△ABC不变
矩形面积与PQ长度有关
建立“面积”与“PQ长度”的联系
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件两条相邻的边长就不能确定,但这个矩形面积有最大值,求面积达到这个最大值时矩形零件相邻的两条边长.
解:
∵四边形PQMN是矩形,
∴ PN//QM,△APN∽△ABC.
设PQ=x mm,则AE=(80-x) mm ,
∵0∴ 当x=40时,矩形PQMN面积取得最大值
此时PN=60mm.
图②
x
x
80-x
120
80
小结:两三角形相似的关系不变,矩形的面积与PQ的长度有关,建立“面积”与“PQ的长度”之间的联系,运用函数关系,确定面积的最大值.
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
分析:
(1)
1
2
3
AD//BC
∠2 =∠3
△PFA∽△ABE
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
证明:
(1)
1
2
3
∵四边形ABCD是正方形,
∴∠B=90°,AD∥BC.
∴∠2 =∠3.
∵ PF⊥AE,
∴∠AFP=90°= ∠B.
∴ △PFA∽△ABE.
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
△PEF∽△EAB
分析:
(2)
相似三角形的判定
△ABE的两个锐角是: ∠EAB和∠AEB
△PFE的两个锐角是: ∠FPE和∠PEF
∠PEF=∠EAB
∠PEF=∠AEB
△PEF∽△AEB
两种情况:
x
4
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
x
4
△PEF∽△EAB
解:
(2)
若△PEF∽△EAB,则∠PEF=∠EAB,
情况一:
∴ PE//AB,
此时四边形ABEP是矩形,
∴ BE=PA=x,
∵ E是BC的中点
∴
即 x=2.
x
4
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
A
B
C
D
E
P
△PEF∽△AEB
解:
(2)
x
4
若△PEF∽△AEB,则∠PEF=∠AEB,
情况二:
∵ ∠PAE=∠AEB
∴ ∠PAE = ∠PEF ,
∴ PE=PA,
在Rt△ABE中,AB=4,BE=2,由勾股定理可得AE=2
∴ AF= AE=
∵ △PEF∽△AEB ,
∴ 即
解得 x=5.
综上所述,x=2 或 x=5
x
F
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
△PEF∽△EAB
分析:
(2)
相似三角形的判定
x
∠PEF=∠EAB
∠PEF=∠AEB
△PEF∽△AEB
两种情况:
小结:解决动点问题时,可视动点不动,用时间表示线段长度;
利用几何条件找到线段之间的数量关系,适当利用相似建立比例关系,列方程并求解
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
分析:
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
分析:
△ PBQ与△ ABC的公共角:∠ B
△PBQ∽△ABC
△PBQ∽△CBA
两种情况
点P,点Q的位置与时间 t 有关
用时间 t 表示距离
解:
设经过 t s,△PBQ与△ABC相似.
情况一:①
∵ △PBQ与△ABC有公共角∠ B,
∴当PQ//AC时,△PBQ∽△ABC,
此时
∵AP=2t cm, AB=8 cm,
∴ PB=(8-2t) cm .
又∵ BQ=4t cm, BC=16 cm,
解得 t=2.
2t
8-2t
4t
16
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
解:
设经过 t s,△PBQ与△ABC相似.
情况二:②
∵ ∠B 为△PBQ与△ABC的公共角,
∴当 时,△PBQ∽△CBA,
由①知, PB=(8-2t) cm,BQ=4t cm,
解得 t=0.8.
2t
8-2t
4t
16
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
综上,如果点P,Q分别从点A,B同时出发,经过0.8 s 或 2 s,△PBQ与△ABC相似.
方法总结:
如果两个三角形有一个角相等,
当没有确定两个三角形相似的对应关系时,两个三角形的相似存在两种情况,
此时要注意分类讨论.
解决动点问题时:
可视动点不动,用时间表示线段长度;
利用几何条件找到线段之间的数量关系,
适当利用相似建立比例关系,列方程并求解
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
例 某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园,小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:
如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C.镜子不动,小亮看着镜面上的标记,他来回走动.走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测量影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥ BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,
请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
根据镜面反射原理证明△ABC∽△EDC
分析:
根据相似三角形的性质计算AB
A
B
C
D
E
G
F
H
M
2.5
2
1.5
16
1.65
根据物体与影子的关系证明△ABF∽△GFH
解:
由题意可得:∠ABC=∠EDC=∠GFH=90°,
∠ACB=∠ECD, ∠AFB=∠GHF,
∴△ABC∽△EDC, △ABF∽△GFH ,
则
即
解得AB=99米.
答:“望月阁”的高AB的长度为99米.
小结:测量高大物体的实际问题,考查了相似三角形的判定和性质,能够找到相似三角形是解题的关键.
A
B
C
D
E
G
F
H
M
2.5
2
1.5
16
1.65
总结
相似的综合应用
相似与函数的综合应用
实际问题中的相似
列函数关系式
线段长的最值
面积的最值
与相似有关的最值问题
动点问题中的相似
一个动点引发的相似
两个动点引发的相似
测量高大建筑物
再 见
沪科版九年级上册数学
相似的综合应用
相似的综合应用
相似三角形的对应角相等,对应边成比例.
相似三角形的性质
如图,△ABC∽△FED
∠ABC=∠FED
∠ACB=∠FDE
∠BAC=∠EFD
相似三角形的性质
如图,若△ABC∽△FED,相似比为k.
AG,FH分别是两个三角形的高线;
AK,FJ分别是两个三角形的中线;
BM,EN分别是两个三角形对应角的角平分线.
相似三角形对应线段的比等于相似比.
相似三角形周长的比等于相似比.
相似三角形面积的比等于相似比的平方.
相似三角形的判定
若DE//BC,
则△ADE∽△ABC.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
“A”型
“X”型
若AB//CD,
则△ABO∽△DCO.
相似三角形的判定
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个三角形相似.
则△ABC∽△FED
则△ABC∽△FED
相似与函数
相似
函数
边的比例关系
两个变量之间的关系
明确变量表示的边
用两个未知数表示所有边
列出与变量有关的比例关系
整理成函数关系式明确自变量取值范围
画图象
求最值
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小
当a>0时,x的值离对称轴x=h越近,y的值越小;
当a<0时,x的值离对称轴x=h越近,y的值越大
利用函数求最值
一次函数最值
二次函数最值
三角形相似
例题 如图,在矩形ABCD中,AB=6,BC=8,E为线段BC上的动点(不与B,C重合).连接DE,过点E作EF⊥DE,EF与线段BA交于点F.设CE=x,BF=y,写出y关于x的函数解析式.
分析:
线段比例关系
△EBF∽△DCE
8
6
列出含有x,y的关系式
整理成函数解析式
x
y
8-x
CE=x,BF=y,CD=AB=6,BC=8,EB=BC-CE=8-x
在矩形ABCD中, ∠B=∠C=90 ,
例题 如图,在矩形ABCD中,AB=6,BC=8,E为线段BC上的动点(不与B,C重合).连接DE,过点E作EF⊥DE,EF与线段BA交于点F.设CE=x,BF=y,写出y关于x的函数解析式.
解:
6
8
小结:相似三角形有关知识与函数相结合时,一般通过相似三角形对应边成比例得到比例式,从而建立两个变量之间的关系.
∴∠BEF+∠DEC=90°
∵CE=x,BF=y,CD=AB=6,BC=8,
x
y
8-x
∴EB=BC-CE=8-x
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABD∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
分析:(1)
1
1
∠BAC=90°,AB=AC
∠BAD= ∠CDE
△ABD∽△DCE
∠B= ∠C=45°
∠ADE=45°
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABC∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
证明:(1)
∵△ABC是等腰三角形, ∠BAC=90°
∴∠B= ∠C =45°
在△ABD中,∠ADB+∠BAD+∠B=180°
∴∠ADB+ ∠BAD=135°
又∵∠ADB+∠EDC +∠ADE=180°且∠ADE=45°
∴∠ADB+ ∠EDC=135°
∴ ∠BAD= ∠CDE
∴ △ABD∽△DCE
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABC∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
分析:(2)
1
1-y
BC=
△ABD∽△DCE
x
y
∠BAC=90°,AB=AC=1
DC= -x
CE=1-y
化为二次函数求最值
例 如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是线段BC边上的一个动点(不与B,C重合).在AC上取一点E,使∠ADE=45°.
(1)求证:△ABC∽△DCE ;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时,AE取得最小值.
解:(2)
小结:将几何问题中两条线段关系表达成了一个二次函数的关系,研究线段的最小值问题,就转化到了研究二次函数的最值问题.
∵∠BAC=90°, AB=AC=1
∴BC =
∵ BD=x,AE=y
∴CD= , CE=
当 即BD= 时,
y有最小值.
∴
∴
∴
∴
∴
又∵ △ABD∽△DCE
(0
1-y
x
y
1
图②
例题 如图①,有一块三角形余料ABC.它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
问题:(1)加工成的正方形零件的边长为多少?
(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件两条相邻的边长就不能确定,但这个矩形面积有最大值,求面积达到这个最大值时矩形零件相邻的两条边长.
图①
图①
分析:
△APN∽△ABC
PN
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
问题:(1)加工成的正方形零件的边长为多少?
解:设正方形的边长为xmm,则PN=PQ=ED=x.
∵BC=120 ,AD=80,
∴AE=AD-ED=80-x.
∵ PN∥BC,
∴△APN∽△ABC.
∴ ,
∴ ,即 .
得x=48.
所以,正方形零件的边长为48 mm.
图①
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
问题:(1)加工成的正方形零件的边长为多少?
图②
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件两条相邻的边长就不能确定,但这个矩形面积有最大值,求面积达到这个最大值时矩形零件相邻的两条边长.
分析:
△APN∽△ABC不变
矩形面积与PQ长度有关
建立“面积”与“PQ长度”的联系
例题 如图①,有一块三角形余料ABC.它的边BC=120 mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(2)如果原题中所要加工的零件只是一个矩形,如图②,这样,此矩形零件两条相邻的边长就不能确定,但这个矩形面积有最大值,求面积达到这个最大值时矩形零件相邻的两条边长.
解:
∵四边形PQMN是矩形,
∴ PN//QM,△APN∽△ABC.
设PQ=x mm,则AE=(80-x) mm ,
∵0
此时PN=60mm.
图②
x
x
80-x
120
80
小结:两三角形相似的关系不变,矩形的面积与PQ的长度有关,建立“面积”与“PQ的长度”之间的联系,运用函数关系,确定面积的最大值.
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
分析:
(1)
1
2
3
AD//BC
∠2 =∠3
△PFA∽△ABE
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
证明:
(1)
1
2
3
∵四边形ABCD是正方形,
∴∠B=90°,AD∥BC.
∴∠2 =∠3.
∵ PF⊥AE,
∴∠AFP=90°= ∠B.
∴ △PFA∽△ABE.
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
△PEF∽△EAB
分析:
(2)
相似三角形的判定
△ABE的两个锐角是: ∠EAB和∠AEB
△PFE的两个锐角是: ∠FPE和∠PEF
∠PEF=∠EAB
∠PEF=∠AEB
△PEF∽△AEB
两种情况:
x
4
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
x
4
△PEF∽△EAB
解:
(2)
若△PEF∽△EAB,则∠PEF=∠EAB,
情况一:
∴ PE//AB,
此时四边形ABEP是矩形,
∴ BE=PA=x,
∵ E是BC的中点
∴
即 x=2.
x
4
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证:△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
A
B
C
D
E
P
△PEF∽△AEB
解:
(2)
x
4
若△PEF∽△AEB,则∠PEF=∠AEB,
情况二:
∵ ∠PAE=∠AEB
∴ ∠PAE = ∠PEF ,
∴ PE=PA,
在Rt△ABE中,AB=4,BE=2,由勾股定理可得AE=2
∴ AF= AE=
∵ △PEF∽△AEB ,
∴ 即
解得 x=5.
综上所述,x=2 或 x=5
x
F
例题 如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.
(1)求证△PFA∽△ABE.
(2)当点P在射线AD上运动时,设PA=x,
是否存在实数x,使以P,F,E为顶点的三角形与△ABE相似?
若存在,求出x的值;若不存在,说明理由.
△PEF∽△EAB
分析:
(2)
相似三角形的判定
x
∠PEF=∠EAB
∠PEF=∠AEB
△PEF∽△AEB
两种情况:
小结:解决动点问题时,可视动点不动,用时间表示线段长度;
利用几何条件找到线段之间的数量关系,适当利用相似建立比例关系,列方程并求解
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
分析:
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
分析:
△ PBQ与△ ABC的公共角:∠ B
△PBQ∽△ABC
△PBQ∽△CBA
两种情况
点P,点Q的位置与时间 t 有关
用时间 t 表示距离
解:
设经过 t s,△PBQ与△ABC相似.
情况一:①
∵ △PBQ与△ABC有公共角∠ B,
∴当PQ//AC时,△PBQ∽△ABC,
此时
∵AP=2t cm, AB=8 cm,
∴ PB=(8-2t) cm .
又∵ BQ=4t cm, BC=16 cm,
解得 t=2.
2t
8-2t
4t
16
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
解:
设经过 t s,△PBQ与△ABC相似.
情况二:②
∵ ∠B 为△PBQ与△ABC的公共角,
∴当 时,△PBQ∽△CBA,
由①知, PB=(8-2t) cm,BQ=4t cm,
解得 t=0.8.
2t
8-2t
4t
16
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
综上,如果点P,Q分别从点A,B同时出发,经过0.8 s 或 2 s,△PBQ与△ABC相似.
方法总结:
如果两个三角形有一个角相等,
当没有确定两个三角形相似的对应关系时,两个三角形的相似存在两种情况,
此时要注意分类讨论.
解决动点问题时:
可视动点不动,用时间表示线段长度;
利用几何条件找到线段之间的数量关系,
适当利用相似建立比例关系,列方程并求解
例 在△ ABC中,AB=8cm,高BC=16cm,点P从点A开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P,Q分别从点A,B同时出发,经几秒钟△ PBQ与△ ABC相似?
例 某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园,小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:
如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C.镜子不动,小亮看着镜面上的标记,他来回走动.走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测量影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥ BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,
请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
根据镜面反射原理证明△ABC∽△EDC
分析:
根据相似三角形的性质计算AB
A
B
C
D
E
G
F
H
M
2.5
2
1.5
16
1.65
根据物体与影子的关系证明△ABF∽△GFH
解:
由题意可得:∠ABC=∠EDC=∠GFH=90°,
∠ACB=∠ECD, ∠AFB=∠GHF,
∴△ABC∽△EDC, △ABF∽△GFH ,
则
即
解得AB=99米.
答:“望月阁”的高AB的长度为99米.
小结:测量高大物体的实际问题,考查了相似三角形的判定和性质,能够找到相似三角形是解题的关键.
A
B
C
D
E
G
F
H
M
2.5
2
1.5
16
1.65
总结
相似的综合应用
相似与函数的综合应用
实际问题中的相似
列函数关系式
线段长的最值
面积的最值
与相似有关的最值问题
动点问题中的相似
一个动点引发的相似
两个动点引发的相似
测量高大建筑物
再 见
