22.4 位似变换 课件 (33张PPT)
文档属性
| 名称 | 22.4 位似变换 课件 (33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 17:58:22 | ||
图片预览









文档简介
(共33张PPT)
沪科版九年级上册数学
位似变换
位似变化与坐标
位似图形
如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这点叫做位似中心,这时我们说这两个图形关于这点位似,它们的相似比又称为位似比.
分析:
判断是否为位似图形:
① 是否为相似图形;
② 对应顶点的连线是否相交于一点.
下列图形中△ABC∽△DEF,则这两个三角形不是位似图形的是( ).
A B C D
A
2.位似图形对应点的连线或延长线相交于一点;
3.位似图形对应边平行(或在同一条直线上);
4.位似图形对应角相等.
1.位似图形上任意一对对应点到位似中心的距离的比等于相似比;
位似的性质
位似中心
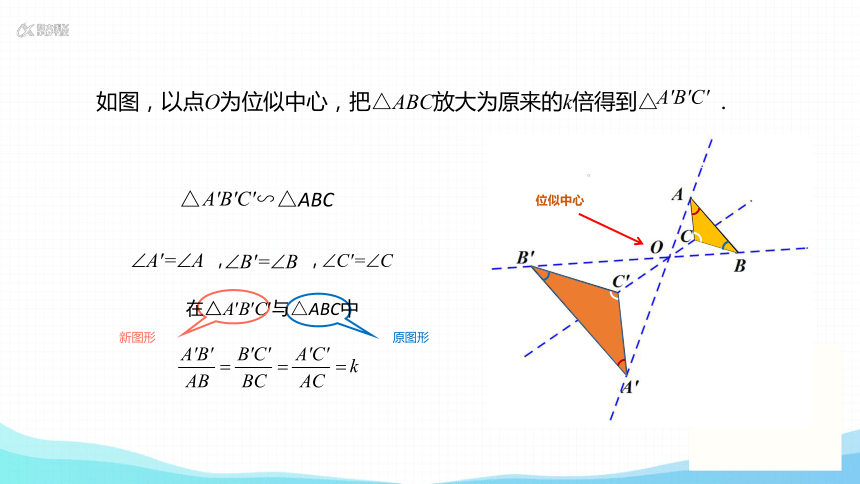
, ,
如图,以点O为位似中心,把△ABC放大为原来的k倍得到△ .
△ ∽△ABC
新图形
原图形
在△A′B′C′与△ABC中
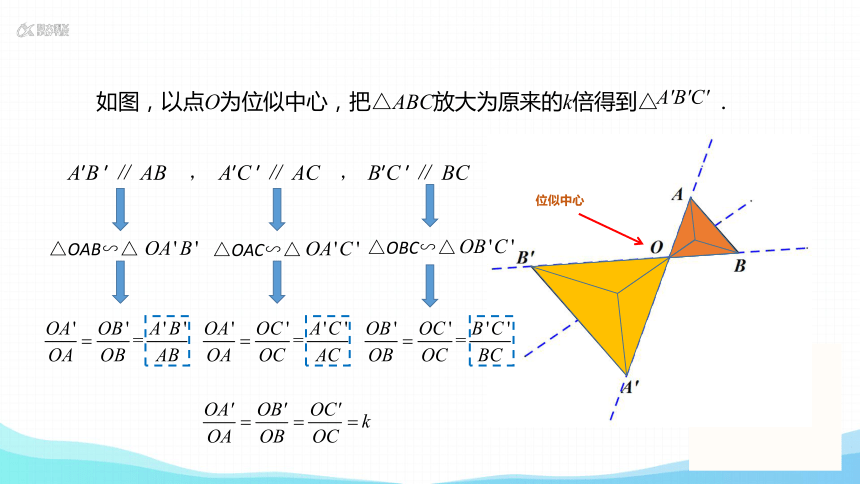
A′B ′ ∥ AB , A′C ′ ∥ AC , B′C ′ ∥ BC
位似中心
如图,以点O为位似中心,把△ABC放大为原来的k倍得到△ .
△OAB∽△
△OAC∽△
△OBC∽△
位似的性质
求出AC
求出A′C′
分析:
在Rt△ACD 中,
法一
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1) ,则A′C′ = .
过点C作CD⊥x轴于点D
O
D
解:
∵△ABC 与△A′B′C′是两位似图形,
在Rt△ACD中,
法一 过点C作CD垂直于x轴,垂足为D,CD⊥AD,则D( ,0)
∴ .
∴ .
∵点A(-1 ,0 ) ,点C( ,1) ,
∴ .
O
D
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1) ,则A′C′ = .
△ABC 与△A′B′C′是位似图形
分析:
法二
作CD⊥x轴,C′ D′ ⊥x轴
位似的性质
△OCD ∽△OC′D′且D( ,0)
O
D′
D
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1),则A′C′ = .
在Rt△ C′D′A′中,
解:
∵△ABC 与△A′B′C′是以坐标原点O为位似中心的位似图形,
法二:连接OC ′ ,过点C作CD垂直于x轴,过点C′作C′D′垂直于x轴.
∴ .
∴ OA′=2.
在Rt△ C′D′A′中,
O
D′
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1),则A′C′ = .
又∵A(-1,0),
∵CD⊥x轴,C′ D′ ⊥x轴, C( ,1),
∴ △OCD ∽△OC′D′ 且D( ,0).
∴
∴ C′D′ =2, OD ′=1 .
D
小结:已知两图形位似,可由位似图形的性质列出比例式,求出相关的边长.
∴ A′D′= OA′+ OD ′=3
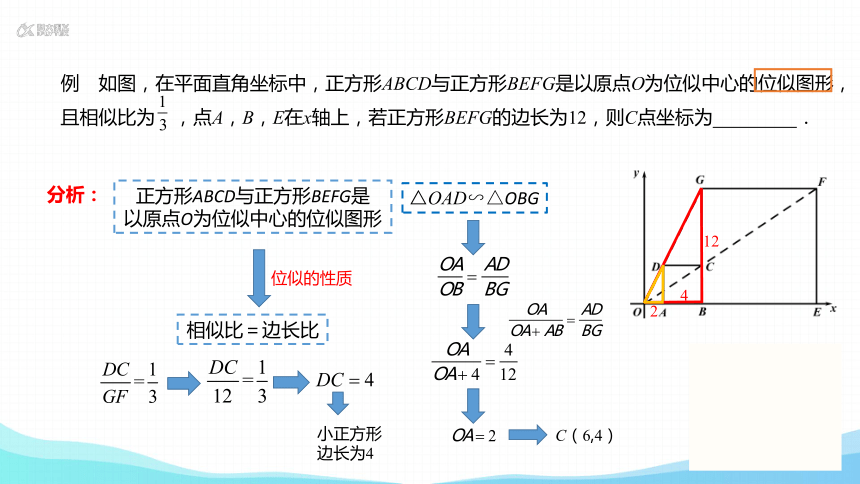
例 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为12,则C点坐标为 .
分析:
正方形ABCD与正方形BEFG是
以原点O为位似中心的位似图形
相似比=边长比
位似的性质
小正方形
边长为4
C(6,4)
12
4
2
△OAD∽△OBG
例 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为12,则C点坐标为 .
解:
∵正方形ABCD与正方形BEFG是以原点O为
位似中心的位似图形,且相似比为 ,
∴ .
∴ BG=12.
∴ AD=BC=4.
∵AD∥BG ,
∴ .
∴ .
∴ OA=2 .
∴ OB=6 .
∴ C点坐标为(6,4).
(6,4)
12
4
∴△OAD∽△OBG.
位似
相似
连接对应点和位似中心
找相似
列比例式
(6,4)
12
4
小结:
相似图形与位似图形的关系:
解题方法
例 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,
且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为12,则C点坐标为 .
分析:
以原点O为位似中心,把这个三角形放大为原来的2倍.
位似中心O在
△ABO与△ 同侧
位似中心O在
△ABO与△ 异侧
例 如图,△ABO三个顶点的坐标分别为A(4,5),B(6,0),O(0,0).以原点O为位似中心,把这个三角形放大为原来的2倍,得到△ .写出△ 三个顶点的坐标.
例 如图,△ABO三个顶点的坐标分别为A(4,5),B(6,0),O(0,0).以原点O为位似中心,把这个三角形放大为原来的2倍,得到△ .写出△ 三个顶点的坐标.
解:
当位似中心O在△ABO与△ 同侧
∵以原点O为位似中心, △ 放大为△ABO的2倍.
∴
∴
又 A(4, 5),B(6,0),O(0,0).
8, 10 120
例 如图,△ABO三个顶点的坐标分别为A(4,5),B(6,0),O(0,0).以原点O为位似中心,把这个三角形放大为原来的2倍,得到△ .写出△ 三个顶点的坐标.
小结:当位似中心在原点时,若位似图形与原来图形的相似比为k,则原图形上的点(x,y),位似变换后变为了点(kx,ky)或(kx,ky)
∴
∴
又∵ A(4,5),B(6,0),O(0,0).
8,10 120
解:
当位似中心O在△ABO与△ 异侧
∵以原点O为位似中心, △ 放大为△ABO的2倍.
分析:
P(a,b)
例 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为
P′ ( , ).已知A,B,C是不共线的三个点,它们经过这种变换后,
得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,
则用等式表示S1与S2的关系为 .
P′( , )
( , )
P(a,b)
位似变换
(缩小)
平移
面积发生改变
面积不变
( , )
P′( , )
例 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为
P′ ( , ).已知A,B,C是不共线的三个点,它们经过这种变换后,
得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,
则用等式表示S1与S2的关系为 .
分析:
点P(a,b)
位似变换
观察坐标的变化
确定:相似比.
面积比等于相似比的平方.
( , )
分析:
S1=4S2
小结:抓住位似变换图形的面积变化,平移图形的面积不变是解题的关键.
例 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为
P′ ( , ).已知A,B,C是不共线的三个点,它们经过这种变换后,
得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,
则用等式表示S1与S2的关系为 .
分析:
例 如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(1 ,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△ ,设点B的对应点 的横坐标为2,则点B的横坐标为 .
过点B作BD⊥x轴,过点 作 ⊥x轴.
分析:
过点B作BD⊥x轴,过点 作 ⊥x轴.
例 如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(1 ,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△ ,设点B的对应点 的横坐标为2,则点B的横坐标为 .
解:
过点B, 分别作BD⊥x轴于点D,BD⊥x轴于点 .
点 的横坐标是2,点C的坐标是(1 ,0) ,
点B,C, 在一条直线上.
点B的横坐标为 .
△ABC的位似图形是△ .
例 如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(1 ,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△ ,设点B的对应点 的横坐标为2,则点B的横坐标为 .
.
∴
.
.
.
.
小结:过所求点向坐标轴作垂线是求点坐标的基本方法,适当的添加辅助线构造相似三角形有助于解决问题.
画位似图形
位似图形作图步骤
(1)确定位似中心
(2)确定原图形中各顶点关于位似中心的对应的点;
(3)描出新图形.
位似中心在图形外部
位似中心在图形内部
位似图形与原图形在位似中心同侧
位似图形与原图形在位似中心异侧
例 如图,已知△ABC的三个顶点的坐标分别为A(3,3),B( 1 ,0 ),C(4,0),以点A为位似中心放大△ABC,得到△AB′C′,使 ,请在图中画出△AB′C′.
相似比为 1:2
小结:关键是找出位似图形与原图形的相似比,再根据画位似图的步骤画图即可.
C′
作法一:
O
D
A
B
C
A'
B'
C'
D'
1.在四边形外任选一点 O .
例 请画出四边形 ABCD 缩小到原来 的图形.
3.顺次连接点 A ′ ,B ′ ,C ′ ,D ′ ,
所得四边形A ′ B ′ C ′ D ′就是所要求的图形.
2.分别在线段 OA,OB,OC,OD上取点 ,
A ′ ,B ′ ,C ′ ,D ′ ,使得 .
作法二:
1.在四边形外任选一点 O .
O
D
A
B
C
A'
B'
C'
D'
例 请画出四边形 ABCD 缩小到原来 的图形.
3.顺次连接点 A ′ ,B ′ ,C ′ ,D ′ ,
所得四边形A ′ B ′ C ′ D ′就是所要求的图形.
2.分别在线段 OA,OB,OC,OD 的反向延长线上取点 ,
A ′ ,B ′ ,C ′ ,D ′ ,使得 .
作法三:
1.在四边形内任选一点 O .
3.顺次连接点 A ′ ,B ′ ,C ′ ,D ′ ,
所得四边形A ′ B ′ C ′ D ′就是所要求的图形.
2.分别在线段 OA,OB,OC,OD 的上取点 ,
A ′ ,B ′ ,C ′ ,D ′ ,使得 .
O
D
A
B
C
A'
B'
C'
D'
例 请画出四边形 ABCD 缩小到原来 的图形.
还有其他的作法吗?
例 请画出四边形 ABCD 缩小到原来 的图形.
作图时要注意
① 确定位似中心(位似中心的位置可随意选择);
② 确定原图形的关键点(如四边形有四个关键点,即它的四个顶点);
③ 确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
符合要求的图形不唯一(所作的图形与所确定的位似中心的位置有关,
并且同一个位似中心的两侧各有一个符合要求的图形).
图形的位似
位似的定义
相似图形
对应顶点的连线相交于一点
位似的性质
位似图形上任意一对对应点到位似中心的距离的比等于相似比
位似图形对应点的连线或延长线相交于一点
位似图形对应边平行(或在同一条直线上)
位似图形对应角相等
位似的作图
确定位似中心
确定原图形中各顶点关于位似中心的对应的点
描出新图形
位似变换
再 见
沪科版九年级上册数学
位似变换
位似变化与坐标
位似图形
如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这点叫做位似中心,这时我们说这两个图形关于这点位似,它们的相似比又称为位似比.
分析:
判断是否为位似图形:
① 是否为相似图形;
② 对应顶点的连线是否相交于一点.
下列图形中△ABC∽△DEF,则这两个三角形不是位似图形的是( ).
A B C D
A
2.位似图形对应点的连线或延长线相交于一点;
3.位似图形对应边平行(或在同一条直线上);
4.位似图形对应角相等.
1.位似图形上任意一对对应点到位似中心的距离的比等于相似比;
位似的性质
位似中心
, ,
如图,以点O为位似中心,把△ABC放大为原来的k倍得到△ .
△ ∽△ABC
新图形
原图形
在△A′B′C′与△ABC中
A′B ′ ∥ AB , A′C ′ ∥ AC , B′C ′ ∥ BC
位似中心
如图,以点O为位似中心,把△ABC放大为原来的k倍得到△ .
△OAB∽△
△OAC∽△
△OBC∽△
位似的性质
求出AC
求出A′C′
分析:
在Rt△ACD 中,
法一
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1) ,则A′C′ = .
过点C作CD⊥x轴于点D
O
D
解:
∵△ABC 与△A′B′C′是两位似图形,
在Rt△ACD中,
法一 过点C作CD垂直于x轴,垂足为D,CD⊥AD,则D( ,0)
∴ .
∴ .
∵点A(-1 ,0 ) ,点C( ,1) ,
∴ .
O
D
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1) ,则A′C′ = .
△ABC 与△A′B′C′是位似图形
分析:
法二
作CD⊥x轴,C′ D′ ⊥x轴
位似的性质
△OCD ∽△OC′D′且D( ,0)
O
D′
D
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1),则A′C′ = .
在Rt△ C′D′A′中,
解:
∵△ABC 与△A′B′C′是以坐标原点O为位似中心的位似图形,
法二:连接OC ′ ,过点C作CD垂直于x轴,过点C′作C′D′垂直于x轴.
∴ .
∴ OA′=2.
在Rt△ C′D′A′中,
O
D′
例 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 ,若点
A(-1,0) , 点C( ,1),则A′C′ = .
又∵A(-1,0),
∵CD⊥x轴,C′ D′ ⊥x轴, C( ,1),
∴ △OCD ∽△OC′D′ 且D( ,0).
∴
∴ C′D′ =2, OD ′=1 .
D
小结:已知两图形位似,可由位似图形的性质列出比例式,求出相关的边长.
∴ A′D′= OA′+ OD ′=3
例 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为12,则C点坐标为 .
分析:
正方形ABCD与正方形BEFG是
以原点O为位似中心的位似图形
相似比=边长比
位似的性质
小正方形
边长为4
C(6,4)
12
4
2
△OAD∽△OBG
例 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为12,则C点坐标为 .
解:
∵正方形ABCD与正方形BEFG是以原点O为
位似中心的位似图形,且相似比为 ,
∴ .
∴ BG=12.
∴ AD=BC=4.
∵AD∥BG ,
∴ .
∴ .
∴ OA=2 .
∴ OB=6 .
∴ C点坐标为(6,4).
(6,4)
12
4
∴△OAD∽△OBG.
位似
相似
连接对应点和位似中心
找相似
列比例式
(6,4)
12
4
小结:
相似图形与位似图形的关系:
解题方法
例 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,
且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为12,则C点坐标为 .
分析:
以原点O为位似中心,把这个三角形放大为原来的2倍.
位似中心O在
△ABO与△ 同侧
位似中心O在
△ABO与△ 异侧
例 如图,△ABO三个顶点的坐标分别为A(4,5),B(6,0),O(0,0).以原点O为位似中心,把这个三角形放大为原来的2倍,得到△ .写出△ 三个顶点的坐标.
例 如图,△ABO三个顶点的坐标分别为A(4,5),B(6,0),O(0,0).以原点O为位似中心,把这个三角形放大为原来的2倍,得到△ .写出△ 三个顶点的坐标.
解:
当位似中心O在△ABO与△ 同侧
∵以原点O为位似中心, △ 放大为△ABO的2倍.
∴
∴
又 A(4, 5),B(6,0),O(0,0).
8, 10 120
例 如图,△ABO三个顶点的坐标分别为A(4,5),B(6,0),O(0,0).以原点O为位似中心,把这个三角形放大为原来的2倍,得到△ .写出△ 三个顶点的坐标.
小结:当位似中心在原点时,若位似图形与原来图形的相似比为k,则原图形上的点(x,y),位似变换后变为了点(kx,ky)或(kx,ky)
∴
∴
又∵ A(4,5),B(6,0),O(0,0).
8,10 120
解:
当位似中心O在△ABO与△ 异侧
∵以原点O为位似中心, △ 放大为△ABO的2倍.
分析:
P(a,b)
例 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为
P′ ( , ).已知A,B,C是不共线的三个点,它们经过这种变换后,
得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,
则用等式表示S1与S2的关系为 .
P′( , )
( , )
P(a,b)
位似变换
(缩小)
平移
面积发生改变
面积不变
( , )
P′( , )
例 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为
P′ ( , ).已知A,B,C是不共线的三个点,它们经过这种变换后,
得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,
则用等式表示S1与S2的关系为 .
分析:
点P(a,b)
位似变换
观察坐标的变化
确定:相似比.
面积比等于相似比的平方.
( , )
分析:
S1=4S2
小结:抓住位似变换图形的面积变化,平移图形的面积不变是解题的关键.
例 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为
P′ ( , ).已知A,B,C是不共线的三个点,它们经过这种变换后,
得到的对应点分别为A′,B′,C′.若△ABC的面积为S1,△A′B′C′的面积为S2,
则用等式表示S1与S2的关系为 .
分析:
例 如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(1 ,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△ ,设点B的对应点 的横坐标为2,则点B的横坐标为 .
过点B作BD⊥x轴,过点 作 ⊥x轴.
分析:
过点B作BD⊥x轴,过点 作 ⊥x轴.
例 如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(1 ,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△ ,设点B的对应点 的横坐标为2,则点B的横坐标为 .
解:
过点B, 分别作BD⊥x轴于点D,BD⊥x轴于点 .
点 的横坐标是2,点C的坐标是(1 ,0) ,
点B,C, 在一条直线上.
点B的横坐标为 .
△ABC的位似图形是△ .
例 如图,△ABC中,A,B两个顶点在x轴上方,点C的坐标是(1 ,0),以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,得到△ ,设点B的对应点 的横坐标为2,则点B的横坐标为 .
.
∴
.
.
.
.
小结:过所求点向坐标轴作垂线是求点坐标的基本方法,适当的添加辅助线构造相似三角形有助于解决问题.
画位似图形
位似图形作图步骤
(1)确定位似中心
(2)确定原图形中各顶点关于位似中心的对应的点;
(3)描出新图形.
位似中心在图形外部
位似中心在图形内部
位似图形与原图形在位似中心同侧
位似图形与原图形在位似中心异侧
例 如图,已知△ABC的三个顶点的坐标分别为A(3,3),B( 1 ,0 ),C(4,0),以点A为位似中心放大△ABC,得到△AB′C′,使 ,请在图中画出△AB′C′.
相似比为 1:2
小结:关键是找出位似图形与原图形的相似比,再根据画位似图的步骤画图即可.
C′
作法一:
O
D
A
B
C
A'
B'
C'
D'
1.在四边形外任选一点 O .
例 请画出四边形 ABCD 缩小到原来 的图形.
3.顺次连接点 A ′ ,B ′ ,C ′ ,D ′ ,
所得四边形A ′ B ′ C ′ D ′就是所要求的图形.
2.分别在线段 OA,OB,OC,OD上取点 ,
A ′ ,B ′ ,C ′ ,D ′ ,使得 .
作法二:
1.在四边形外任选一点 O .
O
D
A
B
C
A'
B'
C'
D'
例 请画出四边形 ABCD 缩小到原来 的图形.
3.顺次连接点 A ′ ,B ′ ,C ′ ,D ′ ,
所得四边形A ′ B ′ C ′ D ′就是所要求的图形.
2.分别在线段 OA,OB,OC,OD 的反向延长线上取点 ,
A ′ ,B ′ ,C ′ ,D ′ ,使得 .
作法三:
1.在四边形内任选一点 O .
3.顺次连接点 A ′ ,B ′ ,C ′ ,D ′ ,
所得四边形A ′ B ′ C ′ D ′就是所要求的图形.
2.分别在线段 OA,OB,OC,OD 的上取点 ,
A ′ ,B ′ ,C ′ ,D ′ ,使得 .
O
D
A
B
C
A'
B'
C'
D'
例 请画出四边形 ABCD 缩小到原来 的图形.
还有其他的作法吗?
例 请画出四边形 ABCD 缩小到原来 的图形.
作图时要注意
① 确定位似中心(位似中心的位置可随意选择);
② 确定原图形的关键点(如四边形有四个关键点,即它的四个顶点);
③ 确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
符合要求的图形不唯一(所作的图形与所确定的位似中心的位置有关,
并且同一个位似中心的两侧各有一个符合要求的图形).
图形的位似
位似的定义
相似图形
对应顶点的连线相交于一点
位似的性质
位似图形上任意一对对应点到位似中心的距离的比等于相似比
位似图形对应点的连线或延长线相交于一点
位似图形对应边平行(或在同一条直线上)
位似图形对应角相等
位似的作图
确定位似中心
确定原图形中各顶点关于位似中心的对应的点
描出新图形
位似变换
再 见
