23.1 锐角三角函数 课件(25张PPT)
文档属性
| 名称 | 23.1 锐角三角函数 课件(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 795.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 17:59:36 | ||
图片预览






文档简介
(共25张PPT)
锐角三角函数
1、锐角三角函数的概念
Rt△ABC中,∠A,∠B,∠C 所对的边分别为 , ,
(1)∠A的对边与斜边的比值是∠A的正弦记作sinA= =
(2)∠A的邻边与斜边的比值是∠A的余弦,记作cosA= =
(3)∠A的对边与邻边的比值是∠A的正切,记作tanA= =
一、锐角三角函数的性质和相互之间的关系
a
c
b
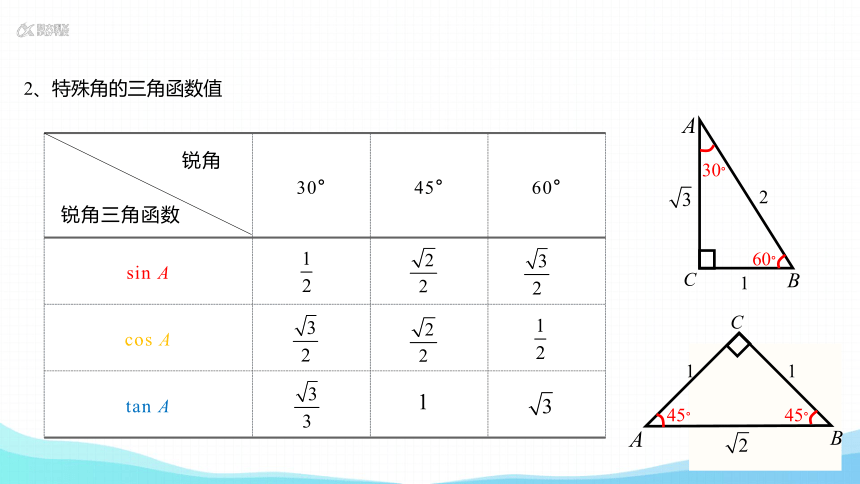
2、特殊角的三角函数值
锐角 锐角三角函数 30° 45° 60°
sin A
cos A
tan A
1
2
60°
30°
45°
45°
1
1
3、锐角三角函数的增减性
(1) 锐角三角函数的范围
0°< <90°,锐角的正弦值的范围是 0< <l,
0°< <90°,锐角的余弦值的范围是 0< <l ;
0°< <90°,锐角的正切值的范围是 >0 .
(2) 锐角三角函数的增减性
在0°-90°之间,锐角的正弦值随角度的增大而增大;
在0°-90°之间,锐角的余弦值随角度的增大而减小;
在0°-90°之间,锐角的正切值随角度的增大而增大.
4、互余角的三角函数间的关系
(1) 互余两角的正余弦之间的关系:
,
即任意一个锐角的正(余)弦值 , 等于它的余角的余(正)弦值.
(2)平方关系:
(3) 商数关系:
A
B
C
a
b
c
sinA=
cosB=
∠A+∠B=90°
sinA=cosB
二、求锐角三角函数的常见方法
1、定义法:
当已知直角三角形的两条边,可直接运用锐角三角函数的定义求解。
2、参数法:
锐角三角函数值实质是直角三角形两边的比值,所以解题中有时需将三角函数转化为线段比,通过设定一个参数,并用含该参数的代数式表示出直角三角形各边的长,然后结合相关条件解决问题。
3、等角代换法:
当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时,可将此角通过等角转换到能够求出三角函数值的直角三角形中,利用“两锐角相等,则三角函数值也相等”来解决。
A
B
C
4、利用网格求三角函数值:
(1) 构造直角三角形
锐角三角函数反映了直角三角形中边与角的关系,所以要求三角函数值,必须将这个角放到直角三角形中。
(2) 转化成在格点上的角
(3) 面积法
(4) 勾股定理法
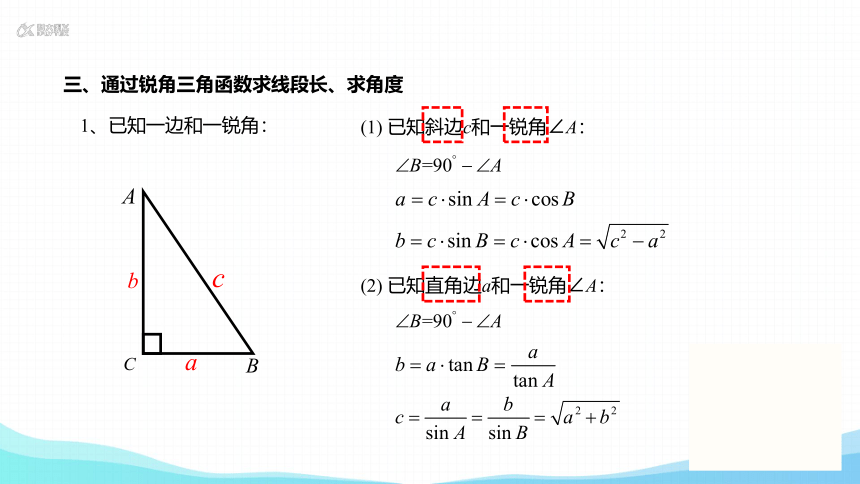
三、通过锐角三角函数求线段长、求角度
1、已知一边和一锐角:
(1) 已知斜边c和一锐角∠A:
(2) 已知直角边a和一锐角∠A:
已知条件 解法步骤
两边
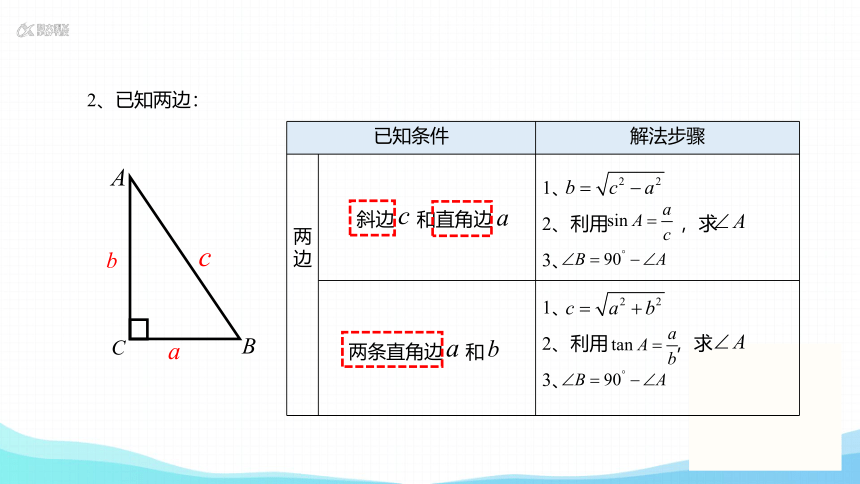
2、已知两边:
斜边 和直角边
两条直角边 和
1、
2、利用 ,求
3、
1、
2、利用 ,求
3、
例. 已知 , 是锐角,则下列答案正确的是( )
A. B. C. D.
分析:
锐角三角函数的增减性
结合 的正弦值
得出结论
解:
∵在 之间,锐角的正弦值随角度 的增大而增大,
且 ,
又
∴ , 故选B.
比较锐角大小
B
例. 化简:
分析:
解:
原式=
=
=
∵a为锐角时, 0< <l ∴
平方关系
互余两角的正余弦之间的关系
锐角三角函数值的范围
例. 在 Rt△ABC中,∠BCA= ,CD是AB的中线,BC=8,CD=5,求 .
分析:
根据CD是中线, ,求出AB的长
再根据勾股定理求出AC的长
得出△ADC是等腰三角形,∠A=∠ACD
由等角代换和锐角三角函数的定义求解
A
C
B
D
8
5
例. 在 Rt△ABC中,∠BCA= ,CD是AB的中线,BC=8,CD=5,求 .
A
C
B
D
解:
如图所示
∵Rt△ABC中, , CD是中线,CD=5,
∴ AB=2CD=10,AD=5
∴△ADC是等腰三角形,
∴∠A=∠ACD
∵在Rt△ABC中,BC=8,AB=10
∴
∴
直角三角形斜边中线的性质
勾股定理
等角代换
8
10
6
5
5
例. 如图,在 边长为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,求 的值 .
分析:
P点不在网格线的格点上
利用网格线构造平行 , 连BE,AE
可以将∠APD转化为一个顶点在格点上的角
得到相等角∠ABE
由锐角三角函数的定义求解
例. 如图,在 边长为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,求 的值 .
解:
如图,连接BE,AE
∵DE∥BC,DE=BC
∴四边形DEBC是平行四边形
∴DC∥BE
∴∠ABE=∠APD
由勾股定理得
BE= ,AE= ,AB=
∵
∴∠AEB=
∴在Rt△ABE中
平行
等角代换
在格点上的角
例. 如图,方格纸中有三个格点A、B、C,求 的值.
分析:
∠ABC不在直角三角形中
过点A做垂线AD
求出垂线段的长
由锐角三角函数的定义求解
利用等面积法:
A
C
B
D
G
E
F
例. 如图,方格纸中有三个格点A、B、C,求 的值.
解:
如图,过点A作AD⊥BC于点D,连接AC
∵
∴ ,∵
∴ , ,又
∴在Rt△ABD中,
作垂线
等面积法
D
A
C
B
G
E
F
还有其他方法吗?
例. 如图,方格纸中有三个格点A、B、C,求 的值.
方法二
解:
由勾股定理易得 , ,
设BD为 ,CD为 ,在Rt△ABD和Rt△ACD中,
由勾股定理得 ,
∴ ,即
∴ , ,
∴在Rt△ABD中,
勾股定理法
A
C
B
D
G
E
F
例. 如图,方格纸中有三个格点A、B、C,求 的值.
总结:
通过分析,这两种方法适用于任何情形下求网格线中的锐角三角函数,而面积法又是这两种方法中最简单的一种,可以将其看成是求网格线中锐角三角函数的万能方法。
A
C
B
D
G
E
F
例. 在 Rt△ABC中,∠C= ,∠A,∠B,∠C 所对的边分别为 , , ,根据下列条件求出直角三角形的其他几个元素:
(1) , ;
(2) ,∠A= .
分析:
画出草图
先确定斜边
结合勾股定理、锐角三角函数定义
得出结果
A
C
B
A
C
B
例. 在 Rt△ABC中,∠C= ,∠A,∠B,∠C 所对的边分别为 , , ,根据下列条件求出直角三角形的其他几个元素:
(1) , ;
(2) ,∠A= .
解:
(1)如图,由勾股定理
∴∠A= ,∠B=
(2)如图,∠B=
,
勾股定理
锐角三角函数
A
C
B
A
C
B
例. 在 Rt△ABC 中,∠C= , ,AB=10,则 BC 的长为多少
分析:
画出草图
已知一锐角的正切值,可得两直角边的倍数关系
用设 法表示直角边
再结合勾股定理求解
A
C
B
例. 在 Rt△ABC 中,∠C= , ,AB=10,则 BC 的长为多少
解:
如图,
∵Rt△ABC 中,
设 ,
∵ ,即
解得 或 (舍)
∴
勾股定理
设 法
A
C
B
总结
锐角三角函数
锐角三角函数的性质和相互之间的关系
通过锐角三角函数求线段长、求角度
已知一边和一锐角
已知两边
特殊角的三角函数值
互余角的三角函数间的关系、同角三角函数间的关系
定义法、参数法
求锐角三角函数的常见方法
增减性
等角代换法
利用网格求三角函数
转化成在格点上的角
构造直角三角形
等面积法
勾股定理法
再 见
锐角三角函数
1、锐角三角函数的概念
Rt△ABC中,∠A,∠B,∠C 所对的边分别为 , ,
(1)∠A的对边与斜边的比值是∠A的正弦记作sinA= =
(2)∠A的邻边与斜边的比值是∠A的余弦,记作cosA= =
(3)∠A的对边与邻边的比值是∠A的正切,记作tanA= =
一、锐角三角函数的性质和相互之间的关系
a
c
b
2、特殊角的三角函数值
锐角 锐角三角函数 30° 45° 60°
sin A
cos A
tan A
1
2
60°
30°
45°
45°
1
1
3、锐角三角函数的增减性
(1) 锐角三角函数的范围
0°< <90°,锐角的正弦值的范围是 0< <l,
0°< <90°,锐角的余弦值的范围是 0< <l ;
0°< <90°,锐角的正切值的范围是 >0 .
(2) 锐角三角函数的增减性
在0°-90°之间,锐角的正弦值随角度的增大而增大;
在0°-90°之间,锐角的余弦值随角度的增大而减小;
在0°-90°之间,锐角的正切值随角度的增大而增大.
4、互余角的三角函数间的关系
(1) 互余两角的正余弦之间的关系:
,
即任意一个锐角的正(余)弦值 , 等于它的余角的余(正)弦值.
(2)平方关系:
(3) 商数关系:
A
B
C
a
b
c
sinA=
cosB=
∠A+∠B=90°
sinA=cosB
二、求锐角三角函数的常见方法
1、定义法:
当已知直角三角形的两条边,可直接运用锐角三角函数的定义求解。
2、参数法:
锐角三角函数值实质是直角三角形两边的比值,所以解题中有时需将三角函数转化为线段比,通过设定一个参数,并用含该参数的代数式表示出直角三角形各边的长,然后结合相关条件解决问题。
3、等角代换法:
当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时,可将此角通过等角转换到能够求出三角函数值的直角三角形中,利用“两锐角相等,则三角函数值也相等”来解决。
A
B
C
4、利用网格求三角函数值:
(1) 构造直角三角形
锐角三角函数反映了直角三角形中边与角的关系,所以要求三角函数值,必须将这个角放到直角三角形中。
(2) 转化成在格点上的角
(3) 面积法
(4) 勾股定理法
三、通过锐角三角函数求线段长、求角度
1、已知一边和一锐角:
(1) 已知斜边c和一锐角∠A:
(2) 已知直角边a和一锐角∠A:
已知条件 解法步骤
两边
2、已知两边:
斜边 和直角边
两条直角边 和
1、
2、利用 ,求
3、
1、
2、利用 ,求
3、
例. 已知 , 是锐角,则下列答案正确的是( )
A. B. C. D.
分析:
锐角三角函数的增减性
结合 的正弦值
得出结论
解:
∵在 之间,锐角的正弦值随角度 的增大而增大,
且 ,
又
∴ , 故选B.
比较锐角大小
B
例. 化简:
分析:
解:
原式=
=
=
∵a为锐角时, 0< <l ∴
平方关系
互余两角的正余弦之间的关系
锐角三角函数值的范围
例. 在 Rt△ABC中,∠BCA= ,CD是AB的中线,BC=8,CD=5,求 .
分析:
根据CD是中线, ,求出AB的长
再根据勾股定理求出AC的长
得出△ADC是等腰三角形,∠A=∠ACD
由等角代换和锐角三角函数的定义求解
A
C
B
D
8
5
例. 在 Rt△ABC中,∠BCA= ,CD是AB的中线,BC=8,CD=5,求 .
A
C
B
D
解:
如图所示
∵Rt△ABC中, , CD是中线,CD=5,
∴ AB=2CD=10,AD=5
∴△ADC是等腰三角形,
∴∠A=∠ACD
∵在Rt△ABC中,BC=8,AB=10
∴
∴
直角三角形斜边中线的性质
勾股定理
等角代换
8
10
6
5
5
例. 如图,在 边长为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,求 的值 .
分析:
P点不在网格线的格点上
利用网格线构造平行 , 连BE,AE
可以将∠APD转化为一个顶点在格点上的角
得到相等角∠ABE
由锐角三角函数的定义求解
例. 如图,在 边长为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,求 的值 .
解:
如图,连接BE,AE
∵DE∥BC,DE=BC
∴四边形DEBC是平行四边形
∴DC∥BE
∴∠ABE=∠APD
由勾股定理得
BE= ,AE= ,AB=
∵
∴∠AEB=
∴在Rt△ABE中
平行
等角代换
在格点上的角
例. 如图,方格纸中有三个格点A、B、C,求 的值.
分析:
∠ABC不在直角三角形中
过点A做垂线AD
求出垂线段的长
由锐角三角函数的定义求解
利用等面积法:
A
C
B
D
G
E
F
例. 如图,方格纸中有三个格点A、B、C,求 的值.
解:
如图,过点A作AD⊥BC于点D,连接AC
∵
∴ ,∵
∴ , ,又
∴在Rt△ABD中,
作垂线
等面积法
D
A
C
B
G
E
F
还有其他方法吗?
例. 如图,方格纸中有三个格点A、B、C,求 的值.
方法二
解:
由勾股定理易得 , ,
设BD为 ,CD为 ,在Rt△ABD和Rt△ACD中,
由勾股定理得 ,
∴ ,即
∴ , ,
∴在Rt△ABD中,
勾股定理法
A
C
B
D
G
E
F
例. 如图,方格纸中有三个格点A、B、C,求 的值.
总结:
通过分析,这两种方法适用于任何情形下求网格线中的锐角三角函数,而面积法又是这两种方法中最简单的一种,可以将其看成是求网格线中锐角三角函数的万能方法。
A
C
B
D
G
E
F
例. 在 Rt△ABC中,∠C= ,∠A,∠B,∠C 所对的边分别为 , , ,根据下列条件求出直角三角形的其他几个元素:
(1) , ;
(2) ,∠A= .
分析:
画出草图
先确定斜边
结合勾股定理、锐角三角函数定义
得出结果
A
C
B
A
C
B
例. 在 Rt△ABC中,∠C= ,∠A,∠B,∠C 所对的边分别为 , , ,根据下列条件求出直角三角形的其他几个元素:
(1) , ;
(2) ,∠A= .
解:
(1)如图,由勾股定理
∴∠A= ,∠B=
(2)如图,∠B=
,
勾股定理
锐角三角函数
A
C
B
A
C
B
例. 在 Rt△ABC 中,∠C= , ,AB=10,则 BC 的长为多少
分析:
画出草图
已知一锐角的正切值,可得两直角边的倍数关系
用设 法表示直角边
再结合勾股定理求解
A
C
B
例. 在 Rt△ABC 中,∠C= , ,AB=10,则 BC 的长为多少
解:
如图,
∵Rt△ABC 中,
设 ,
∵ ,即
解得 或 (舍)
∴
勾股定理
设 法
A
C
B
总结
锐角三角函数
锐角三角函数的性质和相互之间的关系
通过锐角三角函数求线段长、求角度
已知一边和一锐角
已知两边
特殊角的三角函数值
互余角的三角函数间的关系、同角三角函数间的关系
定义法、参数法
求锐角三角函数的常见方法
增减性
等角代换法
利用网格求三角函数
转化成在格点上的角
构造直角三角形
等面积法
勾股定理法
再 见
