23.2 解直角三角形 课件(27张PPT)
文档属性
| 名称 | 23.2 解直角三角形 课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 730.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 18:00:37 | ||
图片预览



文档简介
(共27张PPT)
解直角三角形
首先了解什么是解直角三角形
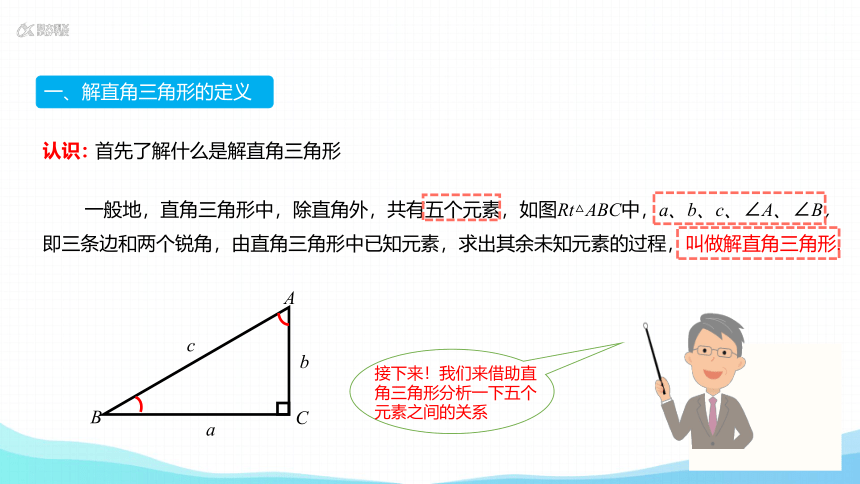
一、解直角三角形的定义
认识:
一般地,直角三角形中,除直角外,共有五个元素,如图Rt△ABC中,a、b、c、∠A、∠B,即三条边和两个锐角,由直角三角形中已知元素,求出其余未知元素的过程,叫做解直角三角形.
接下来!我们来借助直角三角形分析一下五个元素之间的关系
A
B
C
a
c
b
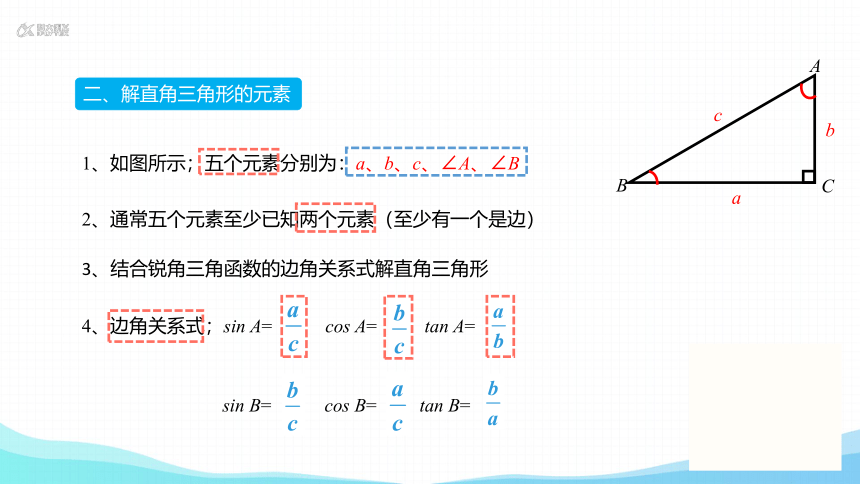
二、解直角三角形的元素
1、如图所示;五个元素分别为:a、b、c、∠A、∠B
2、通常五个元素至少已知两个元素(至少有一个是边)
4、边角关系式;sin A= cos A= tan A=
3、结合锐角三角函数的边角关系式解直角三角形
A
B
C
a
c
b
sin B= cos B= tan B=
作垂线
构造直角三角形
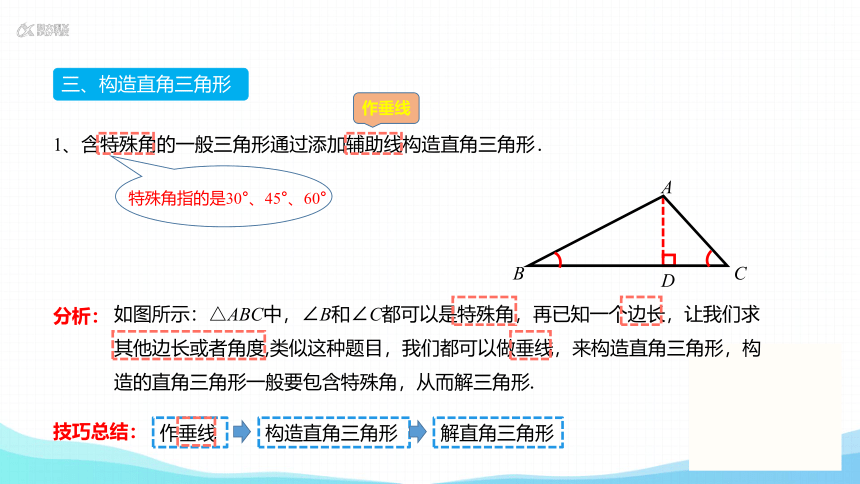
三、构造直角三角形
1、含特殊角的一般三角形通过添加辅助线构造直角三角形.
特殊角指的是30°、45°、60°
如图所示:△ABC中,∠B和∠C都可以是特殊角,再已知一个边长,让我们求其他边长或者角度,类似这种题目,我们都可以做垂线,来构造直角三角形,构造的直角三角形一般要包含特殊角,从而解三角形.
技巧总结:
A
B
C
分析:
解直角三角形
D
作垂线
2、含特殊角的四边形通过添加辅助线构造直角三角形
关于这类题目的解题思路,其实跟上一类很像,虽然是四边形,但是也会有特殊角,
所以我们可以作垂线或者延长线,构造直角三角形.如图;
分析:
如图;类似四边形ABCD,会告诉我们一些特殊角,如∠A、∠C是已知的特殊角,∠B为直角,如图,延长AD和BC交于点E,构造直角三角形,把特殊角包含在直角三角形内,再根据已知边长和边角关系式,解直角三角形.
(1)四边形本身含有特殊角
A
B
C
D
E
同学们!你还可以作垂线构造直角三角形吗?
作垂线或延长线
2
1
A
B
C
D
直角三角形一般包含特殊角
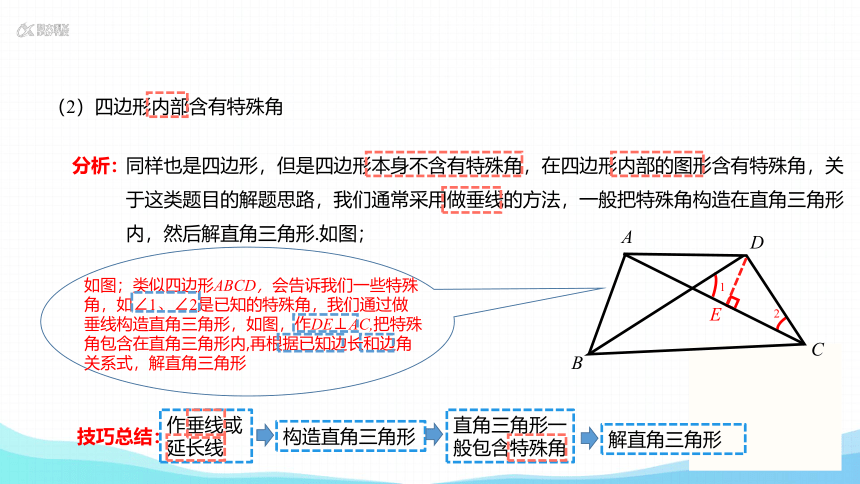
同样也是四边形,但是四边形本身不含有特殊角,在四边形内部的图形含有特殊角,关
于这类题目的解题思路,我们通常采用做垂线的方法,一般把特殊角构造在直角三角形
内,然后解直角三角形.如图;
分析:
构造直角三角形
技巧总结:
解直角三角形
如图;类似四边形ABCD,会告诉我们一些特殊角,如∠1、∠2是已知的特殊角,我们通过做垂线构造直角三角形,如图,作DE⊥AC,把特殊角包含在直角三角形内,再根据已知边长和边角关系式,解直角三角形
E
(2)四边形内部含有特殊角
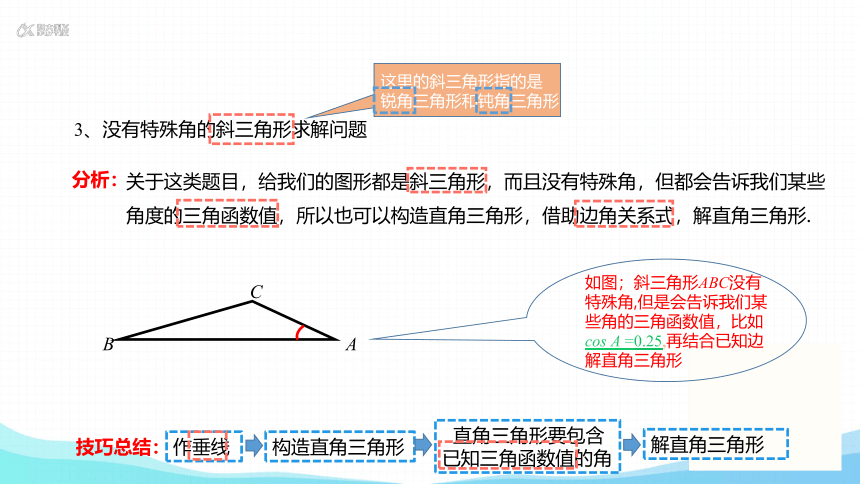
3、没有特殊角的斜三角形求解问题
这里的斜三角形指的是
锐角三角形和钝角三角形
关于这类题目,给我们的图形都是斜三角形,而且没有特殊角,但都会告诉我们某些
角度的三角函数值,所以也可以构造直角三角形,借助边角关系式,解直角三角形.
分析:
直角三角形要包含 已知三角函数值的角
作垂线
构造直角三角形
技巧总结:
解直角三角形
如图;斜三角形ABC没有特殊角,但是会告诉我们某些角的三角函数值,比如
cos A =0.25,再结合已知边解直角三角形
C
A
B
四、解直角三角形的常见类型
1、背靠背型
这类题目,是解直角三角形的常见类型,通常指两个三角形并列背靠背关系,
有着公共边,且这条公共边是解直角三角形的关键.如图;
分析:
A
B
C
D
公共边
如图;△ABD和△ADC就是背靠背,公共边AD是解题的关键,同时也连接着两个三角形的边角关系式,通常要从公共边AD入手,利用方程思想,选择一条边,设其长度为x,再用含有x的代数式表示其他边,从而列方程,解方程,最后求出边或角
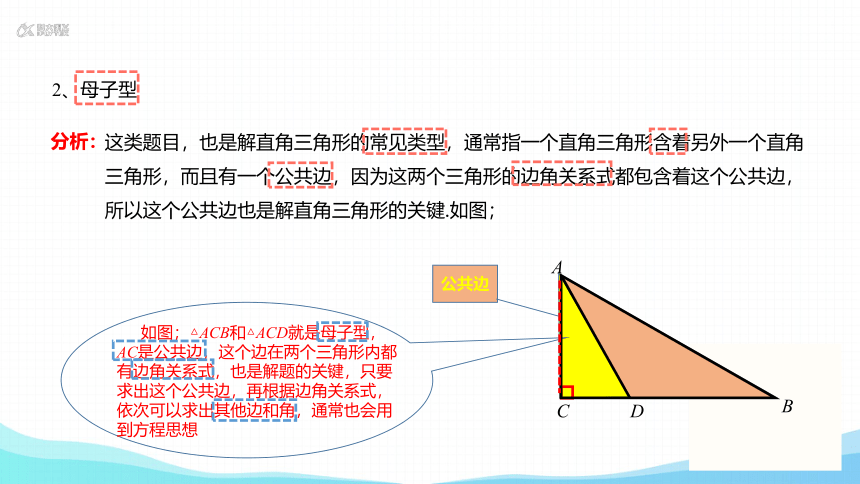
2、母子型
这类题目,也是解直角三角形的常见类型,通常指一个直角三角形含着另外一个直角
三角形,而且有一个公共边,因为这两个三角形的边角关系式都包含着这个公共边,
所以这个公共边也是解直角三角形的关键.如图;
分析:
如图;△ACB和△ACD就是母子型,AC是公共边,这个边在两个三角形内都有边角关系式,也是解题的关键,只要求出这个公共边,再根据边角关系式,依次可以求出其他边和角,通常也会用到方程思想
B
A
C
D
公共边
根据tanB=
例. 如图△ABC中,tan B= ,cos C = ,AC= .求BC的长.
分析:
含特殊角的一般三角形
求出AE=CE=1
根据cosC=
作AE⊥BC
求出∠C=45°
求出BE
A
B
C
E
例. 如图△ABC中,tan B= ,cos C= ,AC= .求BC的长.
解:
总结:
构造直角三角形
解直角三角形
如图,过点A作AE⊥BC于点E,
在Rt△ACE中,CE=AC·cos C=1,
∵cos C= ,∴∠C=45°.
∴AE=CE=1.
含特殊角的一般三角形
在Rt△ABE中,tan B= ,即 = ,
∴BE=3AE=3.
∴BC=BE+CE=4
A
B
C
1
1
3
4
E
60°
例 . 如图所示四边形ABCD,其中AB⊥BC,CD⊥AD,∠A=60°,AB=200,CD=100,求AD、BC的长.
分析:
求出DE和CE
延长AD、BC交于点E
求出AE和BE
Rt△ABE中
Rt△CDE中
可得AD与BC的长
B
A
C
D
E
200
100
∵AB=200,∠A=60°,
BC=BE-CE=200 -200
例. 如图所示四边形ABCD,其中AB⊥BC,CD⊥AD,∠A=60°,AB=200,CD=100,求AD、BC的长.
解:
如图,延长AD和BC交于点E,
∴BE=AB tanA=200 ,AE=2AB=400,
∴∠CED=90°-∠A=30°,
在Rt△CDE中,
总结:
构造直角三角形
含30°角的直角三角形
在Rt△ABE中,
∵CD=100,
含特殊角的四边形
E
60°
B
A
C
D
200
100
∴CE=2CD=200,DE=100 ,
∴AD=AE-DE=400-100
30°
例 . 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,
∠DCE=30°,DE= ,BE= .求CD的长和四边形ABCD的面积.
分析:
得出CD的长
作DH⊥AC
EH=DH=1
Rt△DEH中
Rt△DCH中
求出AC,AB的长
四边形ABCD的面积
A
B
C
D
H
E
1
1
45°
30°
30°
例. 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,
∠DCE=30°,DE= ,BE= .求CD的长和四边形ABCD的面积.
解:
如图,过点D作DH⊥AC于点H.
又∵∠DCE=30°,
∴HC= = ,CD= =2 .
∵∠AEB=∠CED=45°,∠BAC=90°,BE= ,
总结:
构造直角三角形
含30度角的直角三角形
∵∠CED=45°,DH⊥EC,DE= ,
∴EH=DH=DE·cos 45°= × =1.
∴AB=AE=2,
∴AC=AE+EH+HC=2+1+ =3+
= .
= ×2×(3+ )+ ×1×(3+ )
∴S四边形ABCD=S△ABC+S△ADC
等腰直角三角形
A
D
B
C
H
E
1
1
2
2
2
例 . 如图,在△ABC中,点P在AB的延长线上,tanA= ,AB=60,tan∠CBP=2.求点C到直线AB的距离为多少?
分析:
借助已知角的三角函数值
过C作AB的垂线
方程思想
得到Rt△ACD和Rt△BCD
设CD=x
列方程求解
A
B
C
60
x
D
P
即 - =60,
∵AD-BD=AB,
例. 如图,在△ABC中,点P在AB的延长线上,tanA= ,AB=60,tan∠CBP=2.求点C到直线AB的距离为多少?
解:
过C作AB的垂线,交直线AB于点D,
在Rt△BCD中,tan∠CBD= ,
∴BD= ,
总结:
构造直角三角形
解直角三角形的应用
得到Rt△ACD与Rt△BCD.
设CD=x,
在Rt△ACD中,tanA= ,
∴AD= ,
解得,x=30.
方程思想
∴CD=30
即点C到直线AB的距离为30
A
B
C
60
x
15
D
P
例. 如图,在△ABC中,AD是BC边上的高,且tanB=cos∠DAC.求证:AC=BD.
分析:
可证出AC=BD
由于tanB=cos∠DAC
∠B的正切
在Rt△ABD和Rt△ADC中
∠DAC的余弦
A
B
C
D
例. 如图,在△ABC中,AD是BC边上的高,且tanB=cos∠DAC.求证:AC=BD.
∴AC=BD.
∴ = ,
证明:
∵AD是BC上的高,
在Rt△ABD和Rt△ADC中,
总结:
锐角三角函数的定义
解直角三角形
∴AD⊥BC,
∴∠ADB=∠ADC=90°.
∵tanB= ,cos∠DAC= ,
又∵ tanB=cos∠DAC,
A
B
C
D
例. 如图所示,AB=120海里,在B处测得∠MBC=45°,A处测得∠NAC=30°,在海岸线AB上有一灯塔D,AB为东西方向,MB、NA为南北方向, 分别求出AC、BC的距离;(结果保留根号)
分析:
结合已知条件
要求AC、BC的长
作CE⊥AB
考虑构造直角三角形
得Rt△CBE和Rt△CAE
即可得解
N
A
B
C
D
E
M
45°
30°
120
例. 如图所示,AB=120海里,在B处测得∠MBC=45°,A处测得∠NAC=30°,在海岸线AB上有一灯塔D, AB为东西方向,MB、NA为南北方向,分别求出AC、BC的距离;(结果保留根号)
BC= x= 180 -60
∴AC= x=120 -120,
解:
如解图所示,过点C作CE⊥AB于点E,
在Rt△CBE中,BE=CE=x,
在Rt△CAE中,AE= x,
总结:
构造直角三角形
解直角三角形
根据题意得:∠CBD=45°,∠CAD=60°,
设CE=x,
∵AB=120,
∴x+ x=120,解得x=180-60 ,
方程思想
答:AC距离(120 -120)海里,BC距离(180 -60 )海里;
N
A
B
C
D
M
45°
30°
120
x
x
x
E
例. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知sin∠A= ,BD=2,求BC的长.
分析:
30°角的直角三角形
根据特殊角的正弦值
再根据同角的余角相等
求出∠A=30°
求出∠BCD=∠A=30°
可得BC=2BD
A
B
C
D
2
30°
30°
30°
例. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知sin∠A= ,BD=2,求BC的长.
解:
∵sinA= ,
∴∠A+∠ACD=∠BCD+∠ACD=90°,
∴∠BCD=∠A=30°,
∴∠A=30°,
∵∠ACB=90°,CD⊥AB,
∴BC=2BD=2×2=4.
总结:
含30°角的直角三角形
解直角三角形
特殊角的三角函数值
A
B
C
D
2
30°
4
例. 如图,在Rt△ABC中,∠C=90°,AC=8,∠BAC的平分线AD= ,求∠B的度数及边BC、
AB的长.
分析:
可得∠CAD以及∠B
在Rt△ACD中
根据锐角三角函数的概念
已知斜边、直角边
解直角三角形
从而解直角三角形求出其余结果
B
A
C
D
8
例. 如图,在Rt△ABC中,∠C=90°,AC=8,∠BAC的平分线 AD= ,求∠B的度数及边BC、
AB的长.
∴AB= = =16.
解:
在Rt△ACD中
∴∠BAD=∠CAD=30°,
即∠CAB=60°.
总结:
解直角三角形
∵cos∠CAD= = 8 = ,
∴∠CAD=30°,
∴∠B=90°-∠CAB=30°.
∵sinB= ,
又∵cosB= ,
特殊角的三角函数值
∴BC=AB cosB= 16× = .
B
A
C
D
8
30°
30°
30°
16
解直角三角形
构造直角三角形
解直角三角形的常见类型
解直角三角形的背靠背型
解直角三角形的母子型
含特殊角的一般三角形
含特殊角的四边形
不含特殊角的斜三角形
再 见
解直角三角形
首先了解什么是解直角三角形
一、解直角三角形的定义
认识:
一般地,直角三角形中,除直角外,共有五个元素,如图Rt△ABC中,a、b、c、∠A、∠B,即三条边和两个锐角,由直角三角形中已知元素,求出其余未知元素的过程,叫做解直角三角形.
接下来!我们来借助直角三角形分析一下五个元素之间的关系
A
B
C
a
c
b
二、解直角三角形的元素
1、如图所示;五个元素分别为:a、b、c、∠A、∠B
2、通常五个元素至少已知两个元素(至少有一个是边)
4、边角关系式;sin A= cos A= tan A=
3、结合锐角三角函数的边角关系式解直角三角形
A
B
C
a
c
b
sin B= cos B= tan B=
作垂线
构造直角三角形
三、构造直角三角形
1、含特殊角的一般三角形通过添加辅助线构造直角三角形.
特殊角指的是30°、45°、60°
如图所示:△ABC中,∠B和∠C都可以是特殊角,再已知一个边长,让我们求其他边长或者角度,类似这种题目,我们都可以做垂线,来构造直角三角形,构造的直角三角形一般要包含特殊角,从而解三角形.
技巧总结:
A
B
C
分析:
解直角三角形
D
作垂线
2、含特殊角的四边形通过添加辅助线构造直角三角形
关于这类题目的解题思路,其实跟上一类很像,虽然是四边形,但是也会有特殊角,
所以我们可以作垂线或者延长线,构造直角三角形.如图;
分析:
如图;类似四边形ABCD,会告诉我们一些特殊角,如∠A、∠C是已知的特殊角,∠B为直角,如图,延长AD和BC交于点E,构造直角三角形,把特殊角包含在直角三角形内,再根据已知边长和边角关系式,解直角三角形.
(1)四边形本身含有特殊角
A
B
C
D
E
同学们!你还可以作垂线构造直角三角形吗?
作垂线或延长线
2
1
A
B
C
D
直角三角形一般包含特殊角
同样也是四边形,但是四边形本身不含有特殊角,在四边形内部的图形含有特殊角,关
于这类题目的解题思路,我们通常采用做垂线的方法,一般把特殊角构造在直角三角形
内,然后解直角三角形.如图;
分析:
构造直角三角形
技巧总结:
解直角三角形
如图;类似四边形ABCD,会告诉我们一些特殊角,如∠1、∠2是已知的特殊角,我们通过做垂线构造直角三角形,如图,作DE⊥AC,把特殊角包含在直角三角形内,再根据已知边长和边角关系式,解直角三角形
E
(2)四边形内部含有特殊角
3、没有特殊角的斜三角形求解问题
这里的斜三角形指的是
锐角三角形和钝角三角形
关于这类题目,给我们的图形都是斜三角形,而且没有特殊角,但都会告诉我们某些
角度的三角函数值,所以也可以构造直角三角形,借助边角关系式,解直角三角形.
分析:
直角三角形要包含 已知三角函数值的角
作垂线
构造直角三角形
技巧总结:
解直角三角形
如图;斜三角形ABC没有特殊角,但是会告诉我们某些角的三角函数值,比如
cos A =0.25,再结合已知边解直角三角形
C
A
B
四、解直角三角形的常见类型
1、背靠背型
这类题目,是解直角三角形的常见类型,通常指两个三角形并列背靠背关系,
有着公共边,且这条公共边是解直角三角形的关键.如图;
分析:
A
B
C
D
公共边
如图;△ABD和△ADC就是背靠背,公共边AD是解题的关键,同时也连接着两个三角形的边角关系式,通常要从公共边AD入手,利用方程思想,选择一条边,设其长度为x,再用含有x的代数式表示其他边,从而列方程,解方程,最后求出边或角
2、母子型
这类题目,也是解直角三角形的常见类型,通常指一个直角三角形含着另外一个直角
三角形,而且有一个公共边,因为这两个三角形的边角关系式都包含着这个公共边,
所以这个公共边也是解直角三角形的关键.如图;
分析:
如图;△ACB和△ACD就是母子型,AC是公共边,这个边在两个三角形内都有边角关系式,也是解题的关键,只要求出这个公共边,再根据边角关系式,依次可以求出其他边和角,通常也会用到方程思想
B
A
C
D
公共边
根据tanB=
例. 如图△ABC中,tan B= ,cos C = ,AC= .求BC的长.
分析:
含特殊角的一般三角形
求出AE=CE=1
根据cosC=
作AE⊥BC
求出∠C=45°
求出BE
A
B
C
E
例. 如图△ABC中,tan B= ,cos C= ,AC= .求BC的长.
解:
总结:
构造直角三角形
解直角三角形
如图,过点A作AE⊥BC于点E,
在Rt△ACE中,CE=AC·cos C=1,
∵cos C= ,∴∠C=45°.
∴AE=CE=1.
含特殊角的一般三角形
在Rt△ABE中,tan B= ,即 = ,
∴BE=3AE=3.
∴BC=BE+CE=4
A
B
C
1
1
3
4
E
60°
例 . 如图所示四边形ABCD,其中AB⊥BC,CD⊥AD,∠A=60°,AB=200,CD=100,求AD、BC的长.
分析:
求出DE和CE
延长AD、BC交于点E
求出AE和BE
Rt△ABE中
Rt△CDE中
可得AD与BC的长
B
A
C
D
E
200
100
∵AB=200,∠A=60°,
BC=BE-CE=200 -200
例. 如图所示四边形ABCD,其中AB⊥BC,CD⊥AD,∠A=60°,AB=200,CD=100,求AD、BC的长.
解:
如图,延长AD和BC交于点E,
∴BE=AB tanA=200 ,AE=2AB=400,
∴∠CED=90°-∠A=30°,
在Rt△CDE中,
总结:
构造直角三角形
含30°角的直角三角形
在Rt△ABE中,
∵CD=100,
含特殊角的四边形
E
60°
B
A
C
D
200
100
∴CE=2CD=200,DE=100 ,
∴AD=AE-DE=400-100
30°
例 . 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,
∠DCE=30°,DE= ,BE= .求CD的长和四边形ABCD的面积.
分析:
得出CD的长
作DH⊥AC
EH=DH=1
Rt△DEH中
Rt△DCH中
求出AC,AB的长
四边形ABCD的面积
A
B
C
D
H
E
1
1
45°
30°
30°
例. 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,∠CED=45°,
∠DCE=30°,DE= ,BE= .求CD的长和四边形ABCD的面积.
解:
如图,过点D作DH⊥AC于点H.
又∵∠DCE=30°,
∴HC= = ,CD= =2 .
∵∠AEB=∠CED=45°,∠BAC=90°,BE= ,
总结:
构造直角三角形
含30度角的直角三角形
∵∠CED=45°,DH⊥EC,DE= ,
∴EH=DH=DE·cos 45°= × =1.
∴AB=AE=2,
∴AC=AE+EH+HC=2+1+ =3+
= .
= ×2×(3+ )+ ×1×(3+ )
∴S四边形ABCD=S△ABC+S△ADC
等腰直角三角形
A
D
B
C
H
E
1
1
2
2
2
例 . 如图,在△ABC中,点P在AB的延长线上,tanA= ,AB=60,tan∠CBP=2.求点C到直线AB的距离为多少?
分析:
借助已知角的三角函数值
过C作AB的垂线
方程思想
得到Rt△ACD和Rt△BCD
设CD=x
列方程求解
A
B
C
60
x
D
P
即 - =60,
∵AD-BD=AB,
例. 如图,在△ABC中,点P在AB的延长线上,tanA= ,AB=60,tan∠CBP=2.求点C到直线AB的距离为多少?
解:
过C作AB的垂线,交直线AB于点D,
在Rt△BCD中,tan∠CBD= ,
∴BD= ,
总结:
构造直角三角形
解直角三角形的应用
得到Rt△ACD与Rt△BCD.
设CD=x,
在Rt△ACD中,tanA= ,
∴AD= ,
解得,x=30.
方程思想
∴CD=30
即点C到直线AB的距离为30
A
B
C
60
x
15
D
P
例. 如图,在△ABC中,AD是BC边上的高,且tanB=cos∠DAC.求证:AC=BD.
分析:
可证出AC=BD
由于tanB=cos∠DAC
∠B的正切
在Rt△ABD和Rt△ADC中
∠DAC的余弦
A
B
C
D
例. 如图,在△ABC中,AD是BC边上的高,且tanB=cos∠DAC.求证:AC=BD.
∴AC=BD.
∴ = ,
证明:
∵AD是BC上的高,
在Rt△ABD和Rt△ADC中,
总结:
锐角三角函数的定义
解直角三角形
∴AD⊥BC,
∴∠ADB=∠ADC=90°.
∵tanB= ,cos∠DAC= ,
又∵ tanB=cos∠DAC,
A
B
C
D
例. 如图所示,AB=120海里,在B处测得∠MBC=45°,A处测得∠NAC=30°,在海岸线AB上有一灯塔D,AB为东西方向,MB、NA为南北方向, 分别求出AC、BC的距离;(结果保留根号)
分析:
结合已知条件
要求AC、BC的长
作CE⊥AB
考虑构造直角三角形
得Rt△CBE和Rt△CAE
即可得解
N
A
B
C
D
E
M
45°
30°
120
例. 如图所示,AB=120海里,在B处测得∠MBC=45°,A处测得∠NAC=30°,在海岸线AB上有一灯塔D, AB为东西方向,MB、NA为南北方向,分别求出AC、BC的距离;(结果保留根号)
BC= x= 180 -60
∴AC= x=120 -120,
解:
如解图所示,过点C作CE⊥AB于点E,
在Rt△CBE中,BE=CE=x,
在Rt△CAE中,AE= x,
总结:
构造直角三角形
解直角三角形
根据题意得:∠CBD=45°,∠CAD=60°,
设CE=x,
∵AB=120,
∴x+ x=120,解得x=180-60 ,
方程思想
答:AC距离(120 -120)海里,BC距离(180 -60 )海里;
N
A
B
C
D
M
45°
30°
120
x
x
x
E
例. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知sin∠A= ,BD=2,求BC的长.
分析:
30°角的直角三角形
根据特殊角的正弦值
再根据同角的余角相等
求出∠A=30°
求出∠BCD=∠A=30°
可得BC=2BD
A
B
C
D
2
30°
30°
30°
例. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知sin∠A= ,BD=2,求BC的长.
解:
∵sinA= ,
∴∠A+∠ACD=∠BCD+∠ACD=90°,
∴∠BCD=∠A=30°,
∴∠A=30°,
∵∠ACB=90°,CD⊥AB,
∴BC=2BD=2×2=4.
总结:
含30°角的直角三角形
解直角三角形
特殊角的三角函数值
A
B
C
D
2
30°
4
例. 如图,在Rt△ABC中,∠C=90°,AC=8,∠BAC的平分线AD= ,求∠B的度数及边BC、
AB的长.
分析:
可得∠CAD以及∠B
在Rt△ACD中
根据锐角三角函数的概念
已知斜边、直角边
解直角三角形
从而解直角三角形求出其余结果
B
A
C
D
8
例. 如图,在Rt△ABC中,∠C=90°,AC=8,∠BAC的平分线 AD= ,求∠B的度数及边BC、
AB的长.
∴AB= = =16.
解:
在Rt△ACD中
∴∠BAD=∠CAD=30°,
即∠CAB=60°.
总结:
解直角三角形
∵cos∠CAD= = 8 = ,
∴∠CAD=30°,
∴∠B=90°-∠CAB=30°.
∵sinB= ,
又∵cosB= ,
特殊角的三角函数值
∴BC=AB cosB= 16× = .
B
A
C
D
8
30°
30°
30°
16
解直角三角形
构造直角三角形
解直角三角形的常见类型
解直角三角形的背靠背型
解直角三角形的母子型
含特殊角的一般三角形
含特殊角的四边形
不含特殊角的斜三角形
再 见
