23.2解直角三角形的实际应用 课件(24张PPT)
文档属性
| 名称 | 23.2解直角三角形的实际应用 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 585.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 18:01:16 | ||
图片预览




文档简介
(共24张PPT)
解直角三角形的实际应用
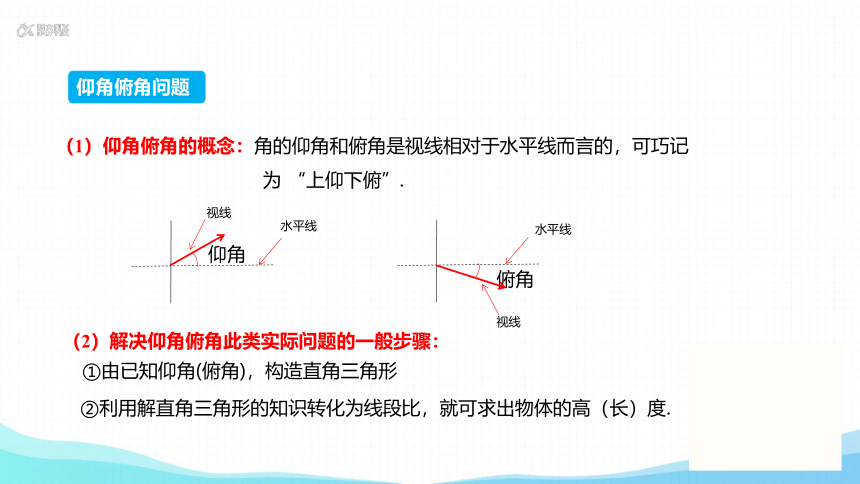
仰角俯角问题
(1)仰角俯角的概念:角的仰角和俯角是视线相对于水平线而言的,可巧记
为 “上仰下俯”.
仰角俯角问题
(2)解决仰角俯角此类实际问题的一般步骤:
②利用解直角三角形的知识转化为线段比,就可求出物体的高(长)度.
①由已知仰角(俯角),构造直角三角形
仰角
视线
水平线
水平线
俯角
视线
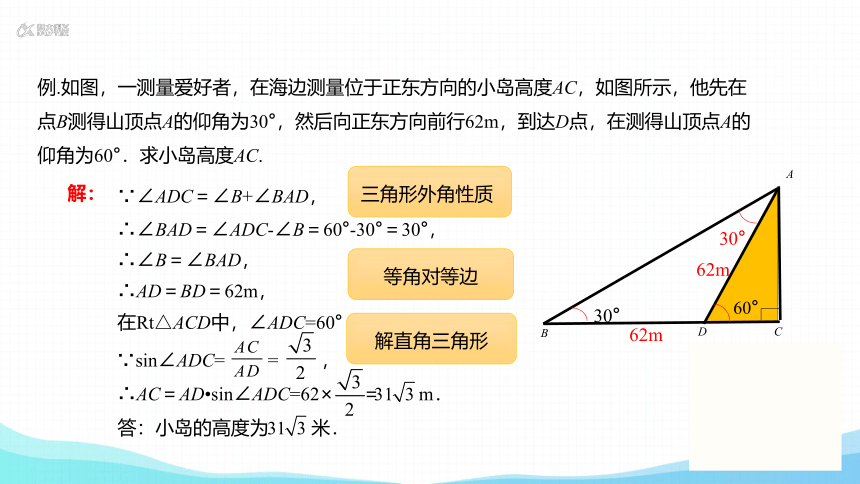
例.如图,一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62m,到达D点,在测得山顶点A的仰角为60°.求小岛高度AC.
分析:
∠ADC=∠B+∠BAD(三角形的外角的性质)
∠B=∠BAD=30°,
A
30°
60°
B
C
D
30°
62m
62m
BD=AD=62m
在Rt△ACD中,根据sin60°= ,求出AC
例.如图,一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62m,到达D点,在测得山顶点A的仰角为60°.求小岛高度AC.
解:
A
30°
60°
B
C
D
∵∠ADC=∠B+∠BAD,
∴∠BAD=∠ADC-∠B=60°-30°=30°,
∴∠B=∠BAD,
∴AD=BD=62m,
在Rt△ACD中,∠ADC=60°
答:小岛的高度为 米.
∵sin∠ADC= = ,
30°
62m
62m
三角形外角性质
等角对等边
解直角三角形
∴AC=AD sin∠ADC=62× = m.
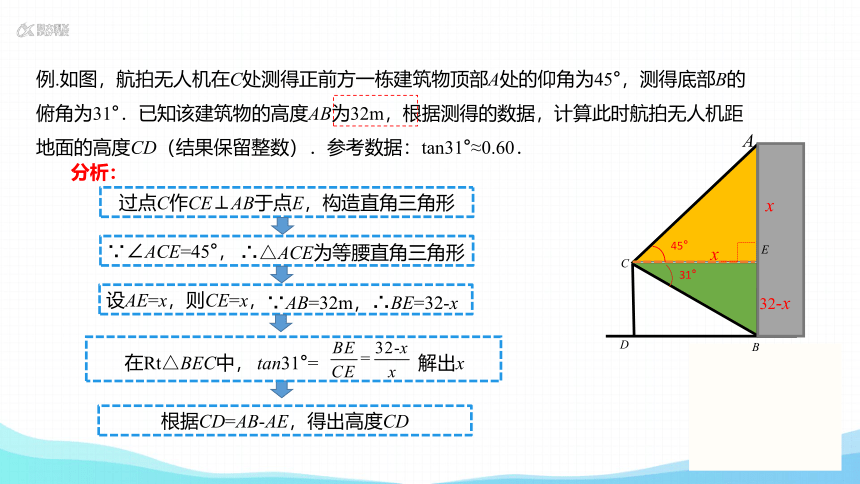
例.如图,航拍无人机在C处测得正前方一栋建筑物顶部A处的仰角为45°,测得底部B的俯角为31°.已知该建筑物的高度AB为32m,根据测得的数据,计算此时航拍无人机距地面的高度CD(结果保留整数).参考数据:tan31°≈0.60.
分析:
D
B
A
C
E
45°
31°
过点C作CE⊥AB于点E,构造直角三角形
∵∠ACE=45°,
设AE=x,则CE=x,
根据CD=AB-AE,得出高度CD
∴△ACE为等腰直角三角形
∵AB=32m,∴BE=32-x
在Rt△BEC中,
tan31°= 解出x
x
x
32-x
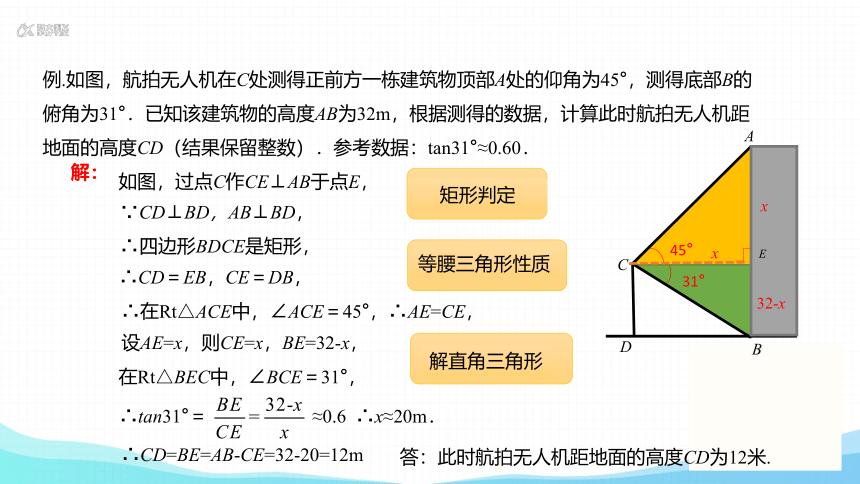
例.如图,航拍无人机在C处测得正前方一栋建筑物顶部A处的仰角为45°,测得底部B的俯角为31°.已知该建筑物的高度AB为32m,根据测得的数据,计算此时航拍无人机距地面的高度CD(结果保留整数).参考数据:tan31°≈0.60.
解:
∵CD⊥BD,AB⊥BD,
∴四边形BDCE是矩形,
矩形判定
等腰三角形性质
解直角三角形
D
B
A
C
45°
31°
∴CD=EB,CE=DB,
在Rt△BEC中,∠BCE=31°,
∴tan31°= ≈0.6 ∴x≈20m.
答:此时航拍无人机距地面的高度CD为12米.
如图,过点C作CE⊥AB于点E,
E
∴在Rt△ACE中,∠ACE=45°,
∴AE=CE,
设AE=x,则CE=x,BE=32-x,
∴CD=BE=AB-CE=32-20=12m
x
x
32-x
坡度坡比问题
h
l
α
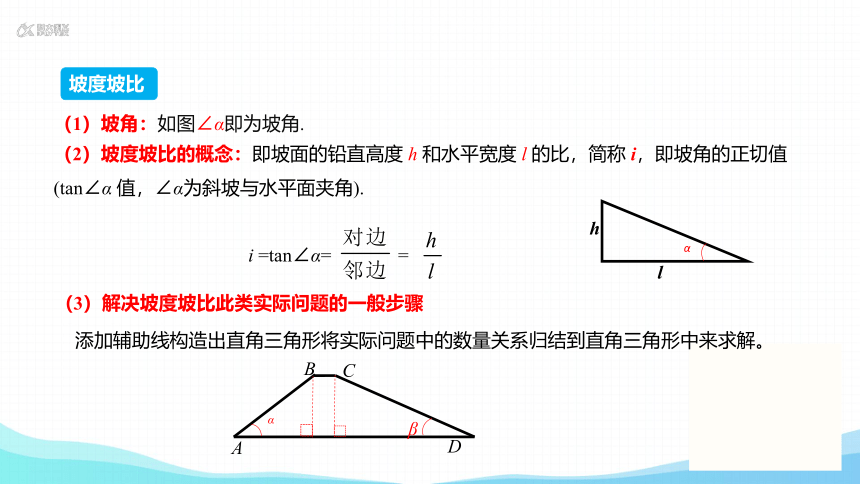
坡度坡比
(3)解决坡度坡比此类实际问题的一般步骤
添加辅助线构造出直角三角形将实际问题中的数量关系归结到直角三角形中来求解。
(1)坡角:如图∠α即为坡角.
A
B
C
D
α
β
(2)坡度坡比的概念:即坡面的铅直高度 h 和水平宽度 l 的比,简称 i,即坡角的正切值 (tan∠α 值,∠α为斜坡与水平面夹角).
i =tan∠α= =
例.如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6m,坝高BE=CF=20m,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,求坝底AD的宽.
分析:
在Rt△CDF中,根据CD坡度i=1:3. 得出DF
根据矩形性质,得出BE=CF=20,BC=EF=6
根据AD=AE+EF+DF,求出AD
E
F
A
B
C
D
30°
在Rt△ABE中,根据tan30°= 得出AE
例.如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6m,坝高BE=CF=20m,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,求坝底AD的宽.
解:
∵BE⊥AD,CF⊥AD,垂足分别为点E,F,
∴EF=BC=6m,
∵BE=CF=20m,
在Rt△CDF中,斜坡CD的坡度i=CF:DF=1:3,
在Rt△ABE中,∠A=30°,
∴DF=3CF=60m
∵tan∠A= ,
∴四边形BCFE是矩形,
∴AE= BE=20 m,
∴AD=AE+EF+DF=(66+20 ) m.
答:坝底AD的宽为(66+20 ) 米
A
B
C
D
E
F
30°
矩形的性质
坡度概念
解直角三角形
6
6
20
20
60
x
60°
30°
分析:
过A点作AF⊥DE,构造矩形ABEF,AB=EF=1.5
在Rt△ABC中,根据AC的坡度,得出BC
设CE=x,在Rt△CDE中,根据tan60°值,得出DE、DF
在Rt△ADF中,根据tan30°值和DF,得出AF
根据AF=BC+CE,列方程,解出x,进而得到DE
1.5
1.5
F
例.如图,某校同学欲测量树DE的高度,他们在正前方A点处测得树顶端D的仰角为30°, 走到台阶下的点C处,测得树顶端D的仰角为60°.已知AB为1.5m,台阶AC的坡度i为1: ,且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
B
C
E
D
A
60°
解:
∴AF=BE,EF=AB=1.5m,
∴DE=4.5m
如图,过点A作AF⊥DE于F,
F
30°
tan60°=
例.如图,某校同学欲测量树DE的高度,他们在正前方A点处测得树顶端D的仰角为30°, 走到台阶下的点C处,测得树顶端D的仰角为60°.已知AB为1.5m,台阶AC的坡度i为1: , 且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
B
C
E
D
A
60°
在Rt△ABC中,
则四边形ABEF为矩形,
设CE=x,∴在Rt△CDE中,
AC的坡度i=AB:BC=1:
∴BC= AB=
∴AF=BE=BC+CE = + x ,
在Rt△ADF中,
tan30°=
答:树DE的高度为4.5m.
∴
∵DF=DE-EF=
∴
解得:
矩形的性质
坡度概念
解直角三角形
1.5
1.5
x
方位角问题
(1)方位角的概念: 指南或指北的方向线与目标方向线构成的小于90°的角,叫做方位角。
在航海、测绘等实际应用中经常用到:
东北方向表示北偏东45°;西北方向表示北偏西45°;
东南方向表示南偏东45°;西南方向表示南偏西45°。
北
南
东
西
O
东北
西北
东南
西南
45°
45°
45°
45°
O
北
南
东
西
30°
60°
B
A
A在O北偏东30°方向
B在O南偏西60°方向
(2)解决方位角此类实际问题的一般步骤:
方位角
①在每个观测点建立方向标,然后根据方位角标出图中已知角的度数.
②添加辅助线构造直角三角形,选择合适的三角函数求边长.
C
北
A
B
60°
东
例.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400m的B处,测得海中灯塔P在它的北偏东45°方向上,灯塔P到环海路的距离PC为多少米?
分析:
由题意:∠PAC=30°,∠PBC=45°,∠BPC=45°AB=400
设PC=x,则BC=x,AC=AB+BC=400+x
解出x,即为所求PC
在Rt△PAC中,根据tan30°值,列方程
北
A
B
P
60°
45°
C
30°
400
45°
45°
x
x
例.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400m的B处,测得海中灯塔P在它的北偏东45°方向上,灯塔P到环海路的距离PC为多少米?
解:
北
A
B
P
60°
45°
C
由题意可得∠PAC=90°-60°=30°
∵∠PBC=45°
∴∠BPC=90°-∠PBC=45°
∴∠BPC=∠PBC
在Rt△PAC中,tan∠PAC=
解出:
答:灯塔P到环海路的距离PC为 米。
设PC=x,∴PC=BC=x AC=400+x
三角形内角和定理
等角对等边定理
解直角三角形
x
x
400
分析:
例.如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处,求B处到C处的距离。
D
北
C
B
A
60°
由题意:∠ACD=30°∠DCB=45°, AC=120
过点C作CD⊥AB于D
30°
120
45°
在Rt△ACD中,根据cos∠ACD= 得出CD
在Rt△BCD中,根据cos∠BCD= 得出BC
在Rt△BCD中,∠BDC=90°,∠DCB=45°
解:
例.如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处,求B处到C处的距离。
答: B处到C处的距离为60 米
∵∠ACD=30°,∴cos∠ACD=
北
C
B
A
60°
如图,过点C作CD⊥AB于D,
D
45°
∴cos∠BCD=
∴CD=AC·cos30°=
在Rt△ACD中 AC=120
解直角三角形
120
分析:
例.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100m,山坡坡度i=1:2,且O、A、B在同一条直线上.求此人所在位置P的铅直高度PB.
过点P分别作PF⊥OC,PB⊥OA,垂足分别为F、B
C
0
P
A
水平地面
山坡
60°
45°
100m
B
F
在Rt△OAC中,由∠OAC=60°,根据 得出OC
由i=1:2,设PB=x,则AB=2x,得出OB、PF和CF
在Rt△PCF中,由∠CPF=45°,得出PF=CF
根据PF=CF列出方程,解出x即为所求PB
x
2x
解:
例.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100m,山坡坡度i=1:2,且O、A、B在同一条直线上.求此人所在位置P的铅直高度PB.
过点P分别作PF⊥OC,PB⊥OA,垂足分别为F、B
C
0
P
A
水平地面
山坡
60°
45°
100m
在Rt△OAC中,∠OAC=60°,OA=100
根据 ,∴OC=OA tan60°= ,
∵i=1:2,设PB=x,则AB=2x.
B
F
∴PF=OB=OA+AB=100+2x,CF=OC-PB= .
在Rt△PCF中,∠CPF=45°
∴PF=CF,∴100+2x= ,
∴x=
答:此人所在位置P的铅直高度PB为 米。
坡比问题
仰俯角问题
构造解直角三角形
x
2x
总结
解直角三角形的实际应用
仰角、俯角
方位角
定义:视线与水平线夹角,上仰下俯
坡度、坡比
定义:坡面的铅直高度 h 和水平宽度 l 的比
定义:指南或指北的方向线与目标方向线构成的小于90°的角
应用:由已知仰角(俯角),构造直角三角形
应用:由坡面、铅直高度和水平宽度,构造直角三角形
应用:在每个观测点建立方向标,构造直角三角形
核心思路:
构造直角三角形
再 见
解直角三角形的实际应用
仰角俯角问题
(1)仰角俯角的概念:角的仰角和俯角是视线相对于水平线而言的,可巧记
为 “上仰下俯”.
仰角俯角问题
(2)解决仰角俯角此类实际问题的一般步骤:
②利用解直角三角形的知识转化为线段比,就可求出物体的高(长)度.
①由已知仰角(俯角),构造直角三角形
仰角
视线
水平线
水平线
俯角
视线
例.如图,一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62m,到达D点,在测得山顶点A的仰角为60°.求小岛高度AC.
分析:
∠ADC=∠B+∠BAD(三角形的外角的性质)
∠B=∠BAD=30°,
A
30°
60°
B
C
D
30°
62m
62m
BD=AD=62m
在Rt△ACD中,根据sin60°= ,求出AC
例.如图,一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62m,到达D点,在测得山顶点A的仰角为60°.求小岛高度AC.
解:
A
30°
60°
B
C
D
∵∠ADC=∠B+∠BAD,
∴∠BAD=∠ADC-∠B=60°-30°=30°,
∴∠B=∠BAD,
∴AD=BD=62m,
在Rt△ACD中,∠ADC=60°
答:小岛的高度为 米.
∵sin∠ADC= = ,
30°
62m
62m
三角形外角性质
等角对等边
解直角三角形
∴AC=AD sin∠ADC=62× = m.
例.如图,航拍无人机在C处测得正前方一栋建筑物顶部A处的仰角为45°,测得底部B的俯角为31°.已知该建筑物的高度AB为32m,根据测得的数据,计算此时航拍无人机距地面的高度CD(结果保留整数).参考数据:tan31°≈0.60.
分析:
D
B
A
C
E
45°
31°
过点C作CE⊥AB于点E,构造直角三角形
∵∠ACE=45°,
设AE=x,则CE=x,
根据CD=AB-AE,得出高度CD
∴△ACE为等腰直角三角形
∵AB=32m,∴BE=32-x
在Rt△BEC中,
tan31°= 解出x
x
x
32-x
例.如图,航拍无人机在C处测得正前方一栋建筑物顶部A处的仰角为45°,测得底部B的俯角为31°.已知该建筑物的高度AB为32m,根据测得的数据,计算此时航拍无人机距地面的高度CD(结果保留整数).参考数据:tan31°≈0.60.
解:
∵CD⊥BD,AB⊥BD,
∴四边形BDCE是矩形,
矩形判定
等腰三角形性质
解直角三角形
D
B
A
C
45°
31°
∴CD=EB,CE=DB,
在Rt△BEC中,∠BCE=31°,
∴tan31°= ≈0.6 ∴x≈20m.
答:此时航拍无人机距地面的高度CD为12米.
如图,过点C作CE⊥AB于点E,
E
∴在Rt△ACE中,∠ACE=45°,
∴AE=CE,
设AE=x,则CE=x,BE=32-x,
∴CD=BE=AB-CE=32-20=12m
x
x
32-x
坡度坡比问题
h
l
α
坡度坡比
(3)解决坡度坡比此类实际问题的一般步骤
添加辅助线构造出直角三角形将实际问题中的数量关系归结到直角三角形中来求解。
(1)坡角:如图∠α即为坡角.
A
B
C
D
α
β
(2)坡度坡比的概念:即坡面的铅直高度 h 和水平宽度 l 的比,简称 i,即坡角的正切值 (tan∠α 值,∠α为斜坡与水平面夹角).
i =tan∠α= =
例.如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6m,坝高BE=CF=20m,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,求坝底AD的宽.
分析:
在Rt△CDF中,根据CD坡度i=1:3. 得出DF
根据矩形性质,得出BE=CF=20,BC=EF=6
根据AD=AE+EF+DF,求出AD
E
F
A
B
C
D
30°
在Rt△ABE中,根据tan30°= 得出AE
例.如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6m,坝高BE=CF=20m,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,求坝底AD的宽.
解:
∵BE⊥AD,CF⊥AD,垂足分别为点E,F,
∴EF=BC=6m,
∵BE=CF=20m,
在Rt△CDF中,斜坡CD的坡度i=CF:DF=1:3,
在Rt△ABE中,∠A=30°,
∴DF=3CF=60m
∵tan∠A= ,
∴四边形BCFE是矩形,
∴AE= BE=20 m,
∴AD=AE+EF+DF=(66+20 ) m.
答:坝底AD的宽为(66+20 ) 米
A
B
C
D
E
F
30°
矩形的性质
坡度概念
解直角三角形
6
6
20
20
60
x
60°
30°
分析:
过A点作AF⊥DE,构造矩形ABEF,AB=EF=1.5
在Rt△ABC中,根据AC的坡度,得出BC
设CE=x,在Rt△CDE中,根据tan60°值,得出DE、DF
在Rt△ADF中,根据tan30°值和DF,得出AF
根据AF=BC+CE,列方程,解出x,进而得到DE
1.5
1.5
F
例.如图,某校同学欲测量树DE的高度,他们在正前方A点处测得树顶端D的仰角为30°, 走到台阶下的点C处,测得树顶端D的仰角为60°.已知AB为1.5m,台阶AC的坡度i为1: ,且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
B
C
E
D
A
60°
解:
∴AF=BE,EF=AB=1.5m,
∴DE=4.5m
如图,过点A作AF⊥DE于F,
F
30°
tan60°=
例.如图,某校同学欲测量树DE的高度,他们在正前方A点处测得树顶端D的仰角为30°, 走到台阶下的点C处,测得树顶端D的仰角为60°.已知AB为1.5m,台阶AC的坡度i为1: , 且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度.
B
C
E
D
A
60°
在Rt△ABC中,
则四边形ABEF为矩形,
设CE=x,∴在Rt△CDE中,
AC的坡度i=AB:BC=1:
∴BC= AB=
∴AF=BE=BC+CE = + x ,
在Rt△ADF中,
tan30°=
答:树DE的高度为4.5m.
∴
∵DF=DE-EF=
∴
解得:
矩形的性质
坡度概念
解直角三角形
1.5
1.5
x
方位角问题
(1)方位角的概念: 指南或指北的方向线与目标方向线构成的小于90°的角,叫做方位角。
在航海、测绘等实际应用中经常用到:
东北方向表示北偏东45°;西北方向表示北偏西45°;
东南方向表示南偏东45°;西南方向表示南偏西45°。
北
南
东
西
O
东北
西北
东南
西南
45°
45°
45°
45°
O
北
南
东
西
30°
60°
B
A
A在O北偏东30°方向
B在O南偏西60°方向
(2)解决方位角此类实际问题的一般步骤:
方位角
①在每个观测点建立方向标,然后根据方位角标出图中已知角的度数.
②添加辅助线构造直角三角形,选择合适的三角函数求边长.
C
北
A
B
60°
东
例.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400m的B处,测得海中灯塔P在它的北偏东45°方向上,灯塔P到环海路的距离PC为多少米?
分析:
由题意:∠PAC=30°,∠PBC=45°,∠BPC=45°AB=400
设PC=x,则BC=x,AC=AB+BC=400+x
解出x,即为所求PC
在Rt△PAC中,根据tan30°值,列方程
北
A
B
P
60°
45°
C
30°
400
45°
45°
x
x
例.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400m的B处,测得海中灯塔P在它的北偏东45°方向上,灯塔P到环海路的距离PC为多少米?
解:
北
A
B
P
60°
45°
C
由题意可得∠PAC=90°-60°=30°
∵∠PBC=45°
∴∠BPC=90°-∠PBC=45°
∴∠BPC=∠PBC
在Rt△PAC中,tan∠PAC=
解出:
答:灯塔P到环海路的距离PC为 米。
设PC=x,∴PC=BC=x AC=400+x
三角形内角和定理
等角对等边定理
解直角三角形
x
x
400
分析:
例.如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处,求B处到C处的距离。
D
北
C
B
A
60°
由题意:∠ACD=30°∠DCB=45°, AC=120
过点C作CD⊥AB于D
30°
120
45°
在Rt△ACD中,根据cos∠ACD= 得出CD
在Rt△BCD中,根据cos∠BCD= 得出BC
在Rt△BCD中,∠BDC=90°,∠DCB=45°
解:
例.如图,一艘海轮位于小岛C的南偏东60°方向,距离小岛120海里的A处,该海轮从A处正北方向航行一段距离后,到达位于小岛C北偏东45°方向的B处,求B处到C处的距离。
答: B处到C处的距离为60 米
∵∠ACD=30°,∴cos∠ACD=
北
C
B
A
60°
如图,过点C作CD⊥AB于D,
D
45°
∴cos∠BCD=
∴CD=AC·cos30°=
在Rt△ACD中 AC=120
解直角三角形
120
分析:
例.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100m,山坡坡度i=1:2,且O、A、B在同一条直线上.求此人所在位置P的铅直高度PB.
过点P分别作PF⊥OC,PB⊥OA,垂足分别为F、B
C
0
P
A
水平地面
山坡
60°
45°
100m
B
F
在Rt△OAC中,由∠OAC=60°,根据 得出OC
由i=1:2,设PB=x,则AB=2x,得出OB、PF和CF
在Rt△PCF中,由∠CPF=45°,得出PF=CF
根据PF=CF列出方程,解出x即为所求PB
x
2x
解:
例.如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100m,山坡坡度i=1:2,且O、A、B在同一条直线上.求此人所在位置P的铅直高度PB.
过点P分别作PF⊥OC,PB⊥OA,垂足分别为F、B
C
0
P
A
水平地面
山坡
60°
45°
100m
在Rt△OAC中,∠OAC=60°,OA=100
根据 ,∴OC=OA tan60°= ,
∵i=1:2,设PB=x,则AB=2x.
B
F
∴PF=OB=OA+AB=100+2x,CF=OC-PB= .
在Rt△PCF中,∠CPF=45°
∴PF=CF,∴100+2x= ,
∴x=
答:此人所在位置P的铅直高度PB为 米。
坡比问题
仰俯角问题
构造解直角三角形
x
2x
总结
解直角三角形的实际应用
仰角、俯角
方位角
定义:视线与水平线夹角,上仰下俯
坡度、坡比
定义:坡面的铅直高度 h 和水平宽度 l 的比
定义:指南或指北的方向线与目标方向线构成的小于90°的角
应用:由已知仰角(俯角),构造直角三角形
应用:由坡面、铅直高度和水平宽度,构造直角三角形
应用:在每个观测点建立方向标,构造直角三角形
核心思路:
构造直角三角形
再 见
