11.3.2 多边形的内角和 同步练习 2023-2024学年八年级上册人教版数学(含答案)
文档属性
| 名称 | 11.3.2 多边形的内角和 同步练习 2023-2024学年八年级上册人教版数学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 268.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 00:00:00 | ||
图片预览


文档简介
11.3.2 多边形的内角和 同步练习
一、单选题
1.如图,将三角形纸片剪掉一角得四边形,设△ABC与四边形BCDE的外角和的度数分别为,,则正确的是( )
A. B.
C. D.无法比较与的大小
2.一个多边形的每一个外角都是,则这个多边形是( )
A.正七边形 B.正六边形 C.正五方形 D.正方形
3.五星红旗是中华人民共和国国旗,旗上的五颗五角星及其相互关系象征着中国共产党领导下的各族人民大团结.五角星是由五个全等的等腰三角形组成,里面形成了一个正五边形,该正五边形的一个内角为( )
A. B. C. D.
4.一个多边形,它的内角和为,则这个多边形是( )
A.五边形 B.十边形 C.十二边形 D.不存在
5.小李家装饰地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则小李不应购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
6.若一个多边形的内角和是它的外角和的2倍,则它的边数是( ).
A.6 B.5 C.4 D.3
7.计算多边形内角和时不小心多输入一个内角,得到和为1290,则这个多边形的边数是( ).
A.8 B.9 C.10 D.11
8.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.6或4 C.5或7 D.5或6或7
二、填空题
9.一个多边形截去一个角后,形成另一个多边形的内角和为,那么原多边形的边数为 .
10.一个边形的所有内角和等于,则的值等于 .
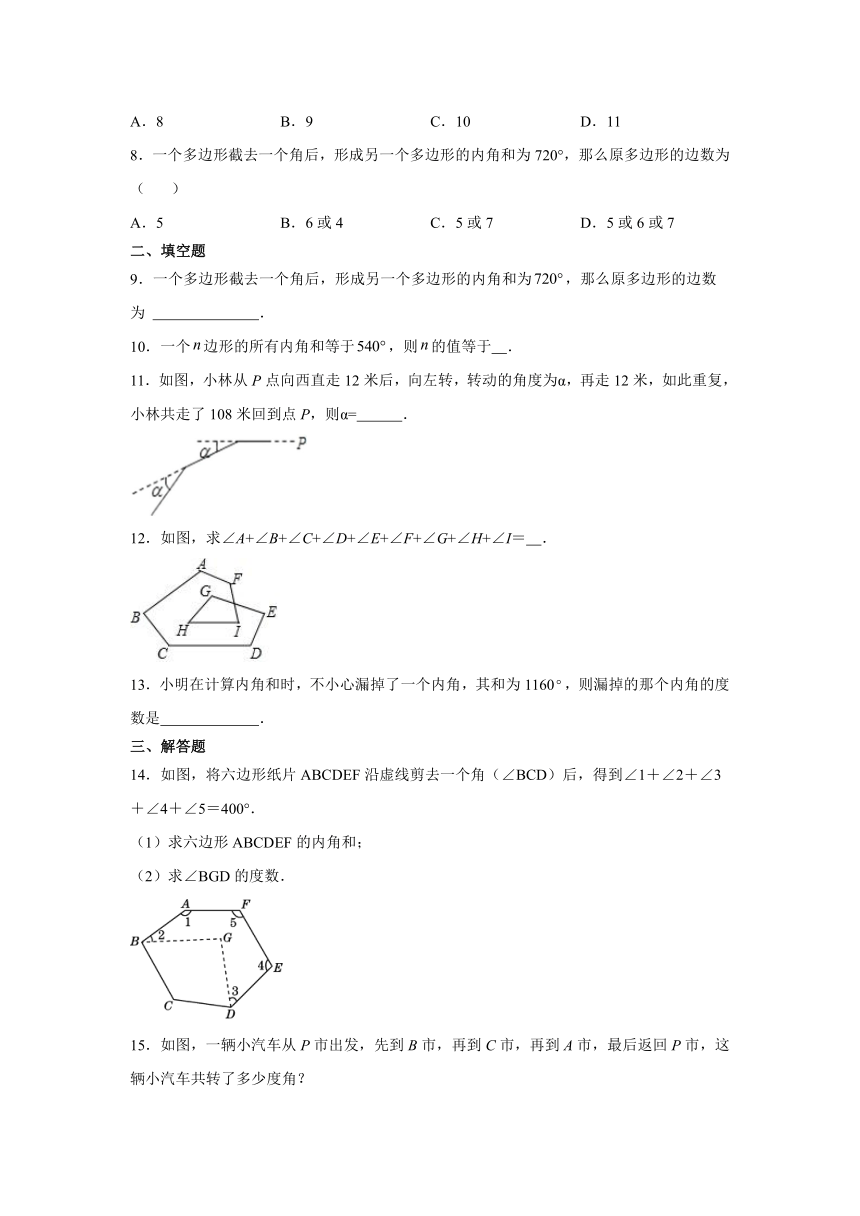
11.如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α= .
12.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I= .
13.小明在计算内角和时,不小心漏掉了一个内角,其和为1160,则漏掉的那个内角的度数是 .
三、解答题
14.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=400°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
15.如图,一辆小汽车从P市出发,先到B市,再到C市,再到A市,最后返回P市,这辆小汽车共转了多少度角?
16.如图,已知五边形ABCDE的各个内角都相等,AF∥CD交DB的延长线于点F,交DE的延长线于点G,若∠GDF=70°,求∠FBA的度数.
17.已知在四边形中,,(,).
(1)_______(用含、的代数式表示).
(2)如图①,若,平分,平分与相邻的外角,请写出与的位置关系,并说明理由.
(3)如图②,为与、相邻的外角平分线所在直线构成的锐角.
①当时,若,试求、;
②小明在作图时,发现不一定存在,请指出、满足什么条件时,不存在.
参考答案
1--8ABBCC ABD
9.5或6或7
10.5
11.40°
12.900°
13.100°
14.解:(1)六边形ABCDEF的内角和为180°×(6﹣2)=720°;
(2)由(1)知六边形ABCDEF的内角和为720°,
∵∠1+∠2+∠3+∠4+∠5=400°,
∴∠GBC+∠C+∠CDG=720°﹣400°=320°,
∴∠BGD=360°﹣(∠GBC+∠C+∠CDG)=360°﹣320°=40°.
∴∠BGD的度数是40°.
15.
【详解】
如图,当小汽车从P出发行驶到B市,由B市向C市行驶时转的角是,由C市向A市行驶时转的角是,由A市向P市行驶时转的角是.
小汽车从P市出发,经B市、C 市、A市,又回到P市,共转.
16.解:对图形进行角标注,
多边形是正五边形,
多边形内角和为:,
,
,
,
,
,
.
17.(1)解:∵在四边形中,
∴,
∵,,
∴;
(2)解:,理由:如答图①,延长交于点,
由(1)知:,
∴当时,,
∵,
∴,
∵平分,平分,
∴,
又∵,
,
∵,,
∴,
.∴,
∴;
(3)解:①如答图②,连接并延长至点,
∵,
∴,
∵平分,
∴
同理可证,.
∵,,
∴,
,;
②如答图③,过点作,
由①得:,,
∵,
∴,
∴.
又∵,
∴当时,,
∴.
∴,
,
,
,
此时,与没有交点,
∴当且时,不存在;
一、单选题
1.如图,将三角形纸片剪掉一角得四边形,设△ABC与四边形BCDE的外角和的度数分别为,,则正确的是( )
A. B.
C. D.无法比较与的大小
2.一个多边形的每一个外角都是,则这个多边形是( )
A.正七边形 B.正六边形 C.正五方形 D.正方形
3.五星红旗是中华人民共和国国旗,旗上的五颗五角星及其相互关系象征着中国共产党领导下的各族人民大团结.五角星是由五个全等的等腰三角形组成,里面形成了一个正五边形,该正五边形的一个内角为( )
A. B. C. D.
4.一个多边形,它的内角和为,则这个多边形是( )
A.五边形 B.十边形 C.十二边形 D.不存在
5.小李家装饰地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则小李不应购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
6.若一个多边形的内角和是它的外角和的2倍,则它的边数是( ).
A.6 B.5 C.4 D.3
7.计算多边形内角和时不小心多输入一个内角,得到和为1290,则这个多边形的边数是( ).
A.8 B.9 C.10 D.11
8.一个多边形截去一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
A.5 B.6或4 C.5或7 D.5或6或7
二、填空题
9.一个多边形截去一个角后,形成另一个多边形的内角和为,那么原多边形的边数为 .
10.一个边形的所有内角和等于,则的值等于 .
11.如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α= .
12.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I= .
13.小明在计算内角和时,不小心漏掉了一个内角,其和为1160,则漏掉的那个内角的度数是 .
三、解答题
14.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=400°.
(1)求六边形ABCDEF的内角和;
(2)求∠BGD的度数.
15.如图,一辆小汽车从P市出发,先到B市,再到C市,再到A市,最后返回P市,这辆小汽车共转了多少度角?
16.如图,已知五边形ABCDE的各个内角都相等,AF∥CD交DB的延长线于点F,交DE的延长线于点G,若∠GDF=70°,求∠FBA的度数.
17.已知在四边形中,,(,).
(1)_______(用含、的代数式表示).
(2)如图①,若,平分,平分与相邻的外角,请写出与的位置关系,并说明理由.
(3)如图②,为与、相邻的外角平分线所在直线构成的锐角.
①当时,若,试求、;
②小明在作图时,发现不一定存在,请指出、满足什么条件时,不存在.
参考答案
1--8ABBCC ABD
9.5或6或7
10.5
11.40°
12.900°
13.100°
14.解:(1)六边形ABCDEF的内角和为180°×(6﹣2)=720°;
(2)由(1)知六边形ABCDEF的内角和为720°,
∵∠1+∠2+∠3+∠4+∠5=400°,
∴∠GBC+∠C+∠CDG=720°﹣400°=320°,
∴∠BGD=360°﹣(∠GBC+∠C+∠CDG)=360°﹣320°=40°.
∴∠BGD的度数是40°.
15.
【详解】
如图,当小汽车从P出发行驶到B市,由B市向C市行驶时转的角是,由C市向A市行驶时转的角是,由A市向P市行驶时转的角是.
小汽车从P市出发,经B市、C 市、A市,又回到P市,共转.
16.解:对图形进行角标注,
多边形是正五边形,
多边形内角和为:,
,
,
,
,
,
.
17.(1)解:∵在四边形中,
∴,
∵,,
∴;
(2)解:,理由:如答图①,延长交于点,
由(1)知:,
∴当时,,
∵,
∴,
∵平分,平分,
∴,
又∵,
,
∵,,
∴,
.∴,
∴;
(3)解:①如答图②,连接并延长至点,
∵,
∴,
∵平分,
∴
同理可证,.
∵,,
∴,
,;
②如答图③,过点作,
由①得:,,
∵,
∴,
∴.
又∵,
∴当时,,
∴.
∴,
,
,
,
此时,与没有交点,
∴当且时,不存在;
