14.2.2 完全平方公式同步练习题(含答案)
文档属性
| 名称 | 14.2.2 完全平方公式同步练习题(含答案) | 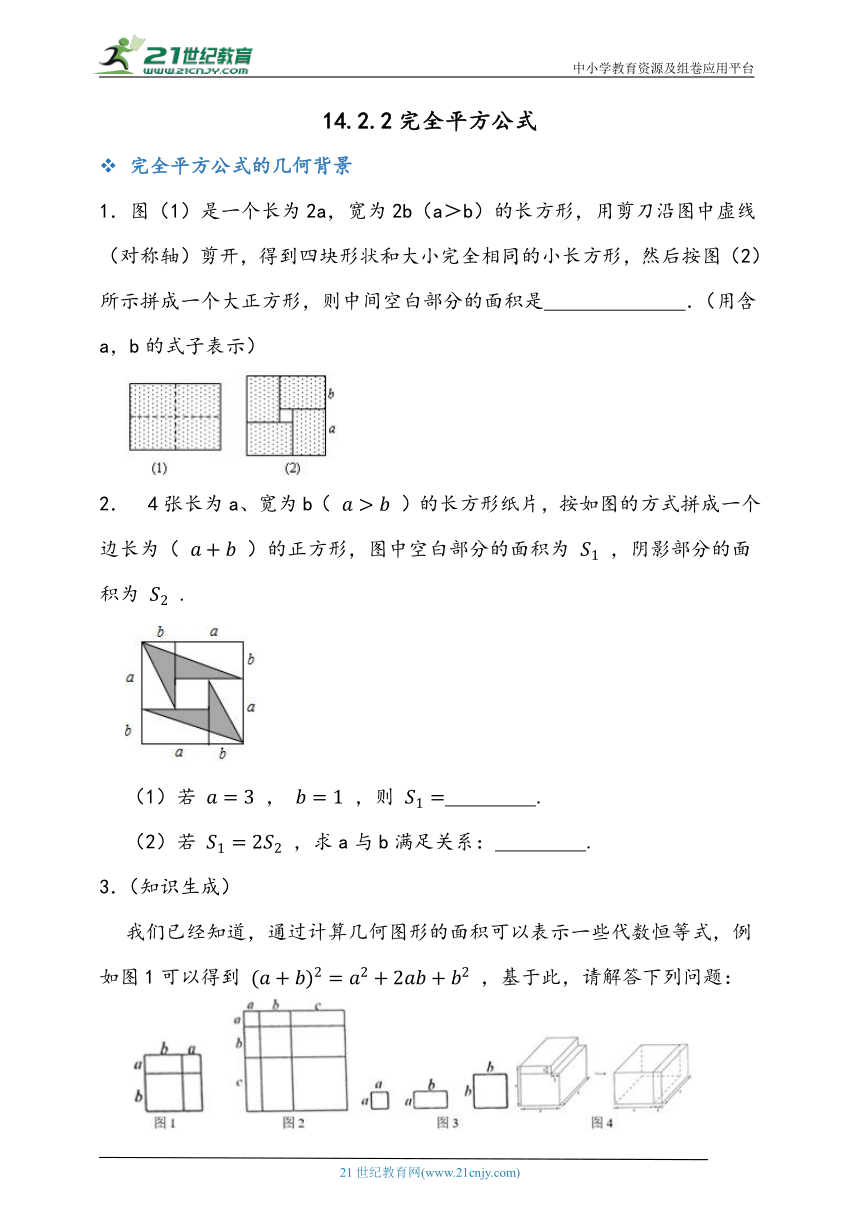 | |
| 格式 | docx | ||
| 文件大小 | 1019.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-26 08:55:12 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
14.2.2完全平方公式
完全平方公式的几何背景
1.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,得到四块形状和大小完全相同的小长方形,然后按图(2)所示拼成一个大正方形,则中间空白部分的面积是 .(用含a,b的式子表示)
2. 4张长为a、宽为b( )的长方形纸片,按如图的方式拼成一个边长为( )的正方形,图中空白部分的面积为 ,阴影部分的面积为 .
(1)若 , ,则 .
(2)若 ,求a与b满足关系: .
3.(知识生成)
我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式,例如图1可以得到 ,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若 , ,则 .
(3)小明同学用图3中 张边长为 的正方形, 张边长为 的正方形, 张宽、长分别为 、 的长方形纸片拼出一个面积为 长方形,则 .
(4)(知识迁移)
事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
4.如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )
A.S1>S2 B.S1≥S2 C.S1<S2 D.S1≤S2
5.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A. B. C.ab D.a2-b2
6.通过计算几何图形的面积可表示一些代数恒等式,下图可表示的代数恒等式是( )
A. B.
C. D.
7.如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a﹣2b)米的正方形,(0<b<),
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米?
完全平方公式及运用
8.我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式,请结合你所学知识,判断下列说法:①当时,;②无论a取任何实数,不等式恒成立;③若,则;正确的有 .
9.若是关于的完全平方式,则 .
10.若x+y=6,xy=7,则x2+y2的值等于 .
11.若则 = .
12.已知正方形的面积是,则正方形的周长是
cm.
13.已知,则的值是 .
14.计算: .
15.已知a-b=7,ab=-10.求:
(1)a2+b2的值;
(2)(a+b)2+2(a-b)2的值.
16.已知 是三边 的长,且满足 ,求 三边的长.
17.数学课上老师出了一道题:计算2962的值,喜欢数学的小亮举手做出这道题,他的解题过程如下:
2962=(300-4)2=3002-2×300×(-4)+42
=90000+2400+16=92416
老师表扬小亮积极发言的同时,也指出了解题中的不符合题意,你认为小亮的解题过程错在哪儿,并给出正确的答案.
18.如图,在矩形ABDE和矩形AGHF中,各分出正方形CDEF、正方形BGHC,矩形ABCF的周长是 14cm ,若正方形CDEF和正方形BGHC的面积之和为29cm2 ,求矩形ABCF的面积.
19.综合与探究
【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如,由图可以得到,基于此,请解答下列问题.
(1)【直接应用】若,,求的值.
(2)【类比应用】若,则 .
(3)【知识迁移】将两块全等的特制直角三角板()按如图所示的方式放置,其中点,,在同一直线上,点,,也在同一直线上,连接,.若,,求一块直角三角板的面积.
答案解析部分
1.【答案】(a﹣b)2
2.【答案】(1)11
(2)a=2b
3.【答案】(1)
(2)30
(3)16
(4)
4.【答案】B
5.【答案】A
6.【答案】B
7.【答案】解:(1)∵2a﹣(a﹣2b)=a+2b,
∴七(2)、七(3)班的清洁区的面积为:(a+2b)(a﹣2b)=(a2﹣4b2)平方米;
(2)(a+2b)2﹣(a﹣2b)2=a2+4ab+4b2﹣(a2﹣4ab+4b2),
=8ab.
答:七(2)、七(3)班的清洁区的面积都为(a2﹣4b2),七(4)班的清洁区的面积比七(1)班的清洁区的面积多8ab平方米.
8.【答案】①②
9.【答案】0或-6
10.【答案】22
11.【答案】84
12.【答案】(4x-16)
13.【答案】14
14.【答案】1
15.【答案】(1)解:∵a﹣b=7,∴(a﹣b)2=49,∴a2﹣2ab+b2=49.
∵ab=﹣10,∴a2﹣2×(﹣10)+b2=49,∴a2+b2=29
(2)解:∵a﹣b=7,∴(a﹣b)2=49,∴a2﹣2ab+b2=49,∴a2+2ab+b2﹣4ab=49,∴(a+b)2﹣4ab=49,∴(a+b)2=49+4ab.
∵ab=﹣10,∴(a+b)2=9,∴(a+b)2+2(a﹣b)2
=9+2×49
=9+98
=107
16.【答案】
即:
.
17.【答案】错在“-2×300×(-4)”,应为“-2×300×4”,公式用错.
∴ =90000-2400+16=87616.
18.【答案】解:设AB=x,AF=y,
∵正方形CDEF和正方形BGHC的面积之和为29cm2
∴x2+y2=29,
∵矩形ABCF的周长是 14cm
∴2(x+y)=14,
∵(x+y)2=x2+2xy+y2,
∴49=29+2xy,
∴xy=10,
∴矩形ABCF的面积为:xy=10
19.【答案】(1)解:∵,
又∵,,
∴,
∴
(2)5
(3)解:∵两块直角三角板全等,
∴,,,
∵点 ,,在同一直线上,点 ,,也在同一直线上,
∴,,
设,.
∵,
又∵,
∴,
∴,
∴.
答:一块直角三角板的面积为24.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
14.2.2完全平方公式
完全平方公式的几何背景
1.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,得到四块形状和大小完全相同的小长方形,然后按图(2)所示拼成一个大正方形,则中间空白部分的面积是 .(用含a,b的式子表示)
2. 4张长为a、宽为b( )的长方形纸片,按如图的方式拼成一个边长为( )的正方形,图中空白部分的面积为 ,阴影部分的面积为 .
(1)若 , ,则 .
(2)若 ,求a与b满足关系: .
3.(知识生成)
我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式,例如图1可以得到 ,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若 , ,则 .
(3)小明同学用图3中 张边长为 的正方形, 张边长为 的正方形, 张宽、长分别为 、 的长方形纸片拼出一个面积为 长方形,则 .
(4)(知识迁移)
事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
4.如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )
A.S1>S2 B.S1≥S2 C.S1<S2 D.S1≤S2
5.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
A. B. C.ab D.a2-b2
6.通过计算几何图形的面积可表示一些代数恒等式,下图可表示的代数恒等式是( )
A. B.
C. D.
7.如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a﹣2b)米的正方形,(0<b<),
(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米?
完全平方公式及运用
8.我们经常利用完全平方公式以及变形公式进行代数式变形.已知关于a的代数式,请结合你所学知识,判断下列说法:①当时,;②无论a取任何实数,不等式恒成立;③若,则;正确的有 .
9.若是关于的完全平方式,则 .
10.若x+y=6,xy=7,则x2+y2的值等于 .
11.若则 = .
12.已知正方形的面积是,则正方形的周长是
cm.
13.已知,则的值是 .
14.计算: .
15.已知a-b=7,ab=-10.求:
(1)a2+b2的值;
(2)(a+b)2+2(a-b)2的值.
16.已知 是三边 的长,且满足 ,求 三边的长.
17.数学课上老师出了一道题:计算2962的值,喜欢数学的小亮举手做出这道题,他的解题过程如下:
2962=(300-4)2=3002-2×300×(-4)+42
=90000+2400+16=92416
老师表扬小亮积极发言的同时,也指出了解题中的不符合题意,你认为小亮的解题过程错在哪儿,并给出正确的答案.
18.如图,在矩形ABDE和矩形AGHF中,各分出正方形CDEF、正方形BGHC,矩形ABCF的周长是 14cm ,若正方形CDEF和正方形BGHC的面积之和为29cm2 ,求矩形ABCF的面积.
19.综合与探究
【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如,由图可以得到,基于此,请解答下列问题.
(1)【直接应用】若,,求的值.
(2)【类比应用】若,则 .
(3)【知识迁移】将两块全等的特制直角三角板()按如图所示的方式放置,其中点,,在同一直线上,点,,也在同一直线上,连接,.若,,求一块直角三角板的面积.
答案解析部分
1.【答案】(a﹣b)2
2.【答案】(1)11
(2)a=2b
3.【答案】(1)
(2)30
(3)16
(4)
4.【答案】B
5.【答案】A
6.【答案】B
7.【答案】解:(1)∵2a﹣(a﹣2b)=a+2b,
∴七(2)、七(3)班的清洁区的面积为:(a+2b)(a﹣2b)=(a2﹣4b2)平方米;
(2)(a+2b)2﹣(a﹣2b)2=a2+4ab+4b2﹣(a2﹣4ab+4b2),
=8ab.
答:七(2)、七(3)班的清洁区的面积都为(a2﹣4b2),七(4)班的清洁区的面积比七(1)班的清洁区的面积多8ab平方米.
8.【答案】①②
9.【答案】0或-6
10.【答案】22
11.【答案】84
12.【答案】(4x-16)
13.【答案】14
14.【答案】1
15.【答案】(1)解:∵a﹣b=7,∴(a﹣b)2=49,∴a2﹣2ab+b2=49.
∵ab=﹣10,∴a2﹣2×(﹣10)+b2=49,∴a2+b2=29
(2)解:∵a﹣b=7,∴(a﹣b)2=49,∴a2﹣2ab+b2=49,∴a2+2ab+b2﹣4ab=49,∴(a+b)2﹣4ab=49,∴(a+b)2=49+4ab.
∵ab=﹣10,∴(a+b)2=9,∴(a+b)2+2(a﹣b)2
=9+2×49
=9+98
=107
16.【答案】
即:
.
17.【答案】错在“-2×300×(-4)”,应为“-2×300×4”,公式用错.
∴ =90000-2400+16=87616.
18.【答案】解:设AB=x,AF=y,
∵正方形CDEF和正方形BGHC的面积之和为29cm2
∴x2+y2=29,
∵矩形ABCF的周长是 14cm
∴2(x+y)=14,
∵(x+y)2=x2+2xy+y2,
∴49=29+2xy,
∴xy=10,
∴矩形ABCF的面积为:xy=10
19.【答案】(1)解:∵,
又∵,,
∴,
∴
(2)5
(3)解:∵两块直角三角板全等,
∴,,,
∵点 ,,在同一直线上,点 ,,也在同一直线上,
∴,,
设,.
∵,
又∵,
∴,
∴,
∴.
答:一块直角三角板的面积为24.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
