24.2.1 点和圆的位置关系---24.4.2圆锥的侧面积和全面积
文档属性
| 名称 | 24.2.1 点和圆的位置关系---24.4.2圆锥的侧面积和全面积 |

|
|
| 格式 | zip | ||
| 文件大小 | 748.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-07 19:50:28 | ||
图片预览




文档简介
( http: / / www. / )§24.2.1 点和圆的位置关系学案
班级: 姓名: 学号:
一、学习任务一
1.探究经过不同的点作圆。
(1)作经过已知点A的圆,这样的圆你能作出多少个?
(2)做经过已知点A,B的圆,这样的圆有多少个?它们的圆心分布有什么特点?
(3)作经过A,B,C,三点的圆,这样的圆有多少个?如何确定它的圆心?
由以上作圆可知过几个点作圆实质是确定圆心和半径,因此过一点的圆有___个,圆心是______,半径是_________.
过两点的圆有____个,圆心是______,半径是_____。过不在同一条直线上的三点_____________.圆心是__半径是__.
2.探究三角形的外接圆:
过三角形ABC三顶点作一个圆。
____________________________________三角形的外接圆.
_____________________________________________外心.
学习任务二:反证法
1.经过同一条直线的三个点能作出一个圆吗?你如何证明你的结论。
2.用反证法证明几何命题的一般步骤是:
二、合作共建(教师寄语:合作的基础是有自己的想法和辨别!)
1.如图是一块破碎的圆形木盖,试确定它的圆心.
2. 在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC的外接圆半径.
3.用反证法证明:一个三角形至少有两个角是锐角。
三、诊断评价(教师寄语:通过练习找出自己的不足! )
1.锐角三角形的外心在 ;直角三角形的外心在 ;钝角三角形的外心在 .
2.若AB=4cm,则过点A、B且半径为3cm的圆有 个.
3.直角三角形三个顶点都在以 为圆心,以 为半径的圆上,直角三角形的外心是 .
4.若Rt△ABC的斜边是AB,它的外接圆面积是121πcm2,则AB= .
5.已知a、b、c是△ABC三边长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5,b=12,c=12
C.a=5,b=12,c=13 D.a=5,b=12,c=14
6.一个三角形的外心在其内部,则这个三角形是( )
A.任意三角形B.直角三角形C.锐角三角形D.钝角三角形
7.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm B.6cm C.7cm D.8cm
8.下列说法错误的是( )
A.过直线上两点和直线外一点,可以确定一个圆
B.任意一个圆都有无数个内接三角形
C.任意一个三角形都有无数个外接圆
D.同一圆的内接三角形的外心都在同一个点上
9.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0的两根,求Rt△ABC的外接圆面积.
10.求边长是6cm的等边三角形的外接圆的半径.
24.2.2直线和圆的位置关系(1)
班级: 姓名: 学号:
【课前预习】
点与圆的位置关系 数量关系
1:知识准备
【课堂活动】
2:探究1:(1)你看过日出吗?你知道太阳升起过程中,太阳和地平线会有几种不同位置关系吗?
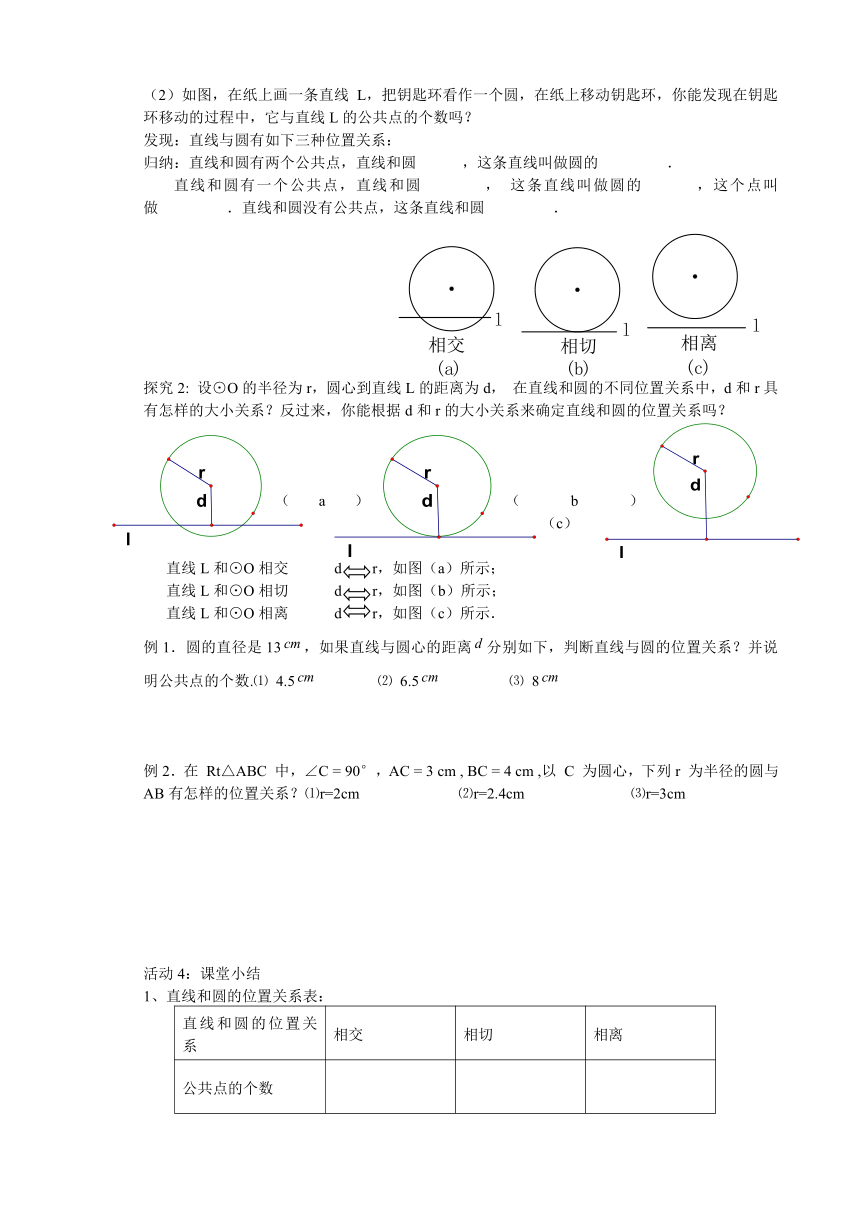
(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点的个数吗?
发现:直线与圆有如下三种位置关系:
归纳:直线和圆有两个公共点,直线和圆 ,这条直线叫做圆的 .
直线和圆有一个公共点,直线和圆 ( http: / / www.21cnjy.com ) ,这条直线叫做圆的 ,这个点叫做 .直线和圆没有公共点,这条直线和圆 .
探究2: 设⊙O的半径为r,圆心到直线L的 ( http: / / www.21cnjy.com )距离为d,在直线和圆的不同位置关系中,d和r具有怎样的大小关系?反过来,你能根据d和r的大小关系来确定直线和圆的位置关系吗?
(a) (b) (c)
直线L和⊙O相交 d r,如图(a)所示;
直线L和⊙O相切 d r,如图(b)所示;
直线L和⊙O相离 d r,如图(c)所示.
例1.圆的直径是13,如果直线与圆心的距离分别如下,判断直线与圆的位置关系?并说明公共点的个数.⑴ 4.5 ⑵ 6.5 ⑶ 8
例2.在 Rt△ABC 中,∠C = 90 ( http: / / www.21cnjy.com )°,AC = 3 cm , BC = 4 cm ,以 C 为圆心,下列r 为半径的圆与AB有怎样的位置关系?⑴r=2cm ⑵r=2.4cm ⑶r=3cm
活动4:课堂小结
1、直线和圆的位置关系表:
直线和圆的位置关系 相交 相切 相离
公共点的个数
公共点名称
直线名称
圆心到直线的距离d与r的关系
2、确定直线与圆的位置关系的方法有____种
(1)根据定义,由___________ _______的个数来判断;
(2)根据性质,由_________________________ 的关系来判断。
24.2.2直线和圆的位置关系(学案纸1)
班级: 姓名: 学号:
随堂训练
1.⊙O的半径是5,点O到直线l的距离为4,则直线l与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
2.如果⊙O的直径为6厘米 ( http: / / www.21cnjy.com ),圆心O到直线AB的距离为5厘米,则直线与AB的位置关系为( )A.相离 B.相切 C.相交 D.不确定
3、已知⊙O的直径为10.(1)、若直线与⊙O相交,则圆心O到直线的距离d ________;
(2)、若直线与⊙O相切,则圆心O到直线的距离d ________;
(3)、若直线与⊙O相离,则圆心O到直线的距离d ________.
4、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
5、已知△ABC 中,AB=AC=5,BC=6,以点A为圆心,以4为半径作⊙A ,⊙A 与直线BC的位置关系怎样。
【课后巩固】
一、判断
1、直线与圆最多有两个公共点。 ( )
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。( )
3、若A、B是⊙O外两点, 则直线AB与⊙O相离。 ( )
4、若C为⊙O内一点,则过点C的直线与⊙O相交。 ( )
二、填空
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
3、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 _ 。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 _。
5、⊙O半径为r,圆心O到直线l的距离为d,且d与r是方程x2-9x+20 =
0的两根,则直线l与⊙O的位置关系是 。
6、如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
1)当直线AB与⊙M相离时, r的取值范围是______________;
2)当直线AB与⊙M相切时, r的取值范围是______________;
3)当直线AB与⊙M有公共点时, r的取值范围是___________.
三、选择题
1.⊙O的半径为4,圆心O到直线l的距 ( http: / / www.21cnjy.com )离为3,则直线l与⊙O的位置关系是( ) A.相交 B.相切 C.相离 D.无法确定
2、设⊙O的半径为4,点O到直线a ( http: / / www.21cnjy.com )的距离为d,若⊙O与直线a至多只有一个公共点,则d为…( )A、d≤4 B、d<4 C、d≥4 D、d=4
3、设⊙p的半径为4cm,直线l上 ( http: / / www.21cnjy.com )一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相切或相交
四、解答题
如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?为什么?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?
24.2.3切线的性质
班级: 姓名: 学号:
学习目标:1.记住切线的性质. 2.能利用切线的性质进行计算和证明
一.忆一忆 : 的直线是圆的切线 .
判断:1. 经过半径外端的直线是圆的切线 ( )
2. 垂直于半径的直线是圆的切线 ( )
3. 经过直径的外端且垂直于这条直径的直线是圆的切线( )
二.探究新知:
如图BC是⊙O的切线,切点为A,则BC经过切点 且BC与OA的位置关系为 。
三. 基础训练
1.如图所示,PA为⊙O的切线,切点为A, PA=, 则⊙O的半径为
2.如图AB与⊙O相切于点B,AO的延长线交⊙O于点C, 连接BC,若,则
3.如图AB与⊙O相切于点A,BO交⊙O于点C, ,则
4.已知直线CD与⊙O相切于C,AB为直径,若,则大小为
5.如图PT切⊙O于点T,若PT=4,PA=2, 则⊙O的半径为
6. 如图中,AB=AC,∠BAC=120°,BC与⊙A相切于点D与BA相交于E,则∠BDE=
7如图PA,PB分别切⊙O于A,B 则
四.提高训练
1.如图,AB为⊙O的直径,C为⊙O上的一点,AD与过C点的切线互相垂直于D, 求证:AC平分
2。如图⊙O的直径AB=6㎝,D为⊙O上的一点,且,过D的切线交AB延长线于C .求:①的度数 ②AC的长.
当堂检测A 姓名 当堂检测B 姓名
如图,已知⊙O中,AB是直径,过B点作⊙O 如图,已知⊙O中,AB是直径,过D点作⊙O
的切线BC,连结CO.若AD∥OC交⊙O于D. 的切线DC,连结CO.若AD∥OC交⊙O于D.
求证:CD是⊙O的切线. 求证:BC是⊙O的切线.
24.2.4垂径定理、切线的性质及判定
班级: 姓名: 学号:
学习目标:会用综合运用垂径定理、切线的性质及判定进行计算和证明.
一、忆一忆:
1.垂直于弦的直径的性质(垂径定理):
垂直于弦的直径 ,并且平分
已知:如图,CD是直径,与弦AB交于点M.
∵CD⊥AB ∴ AM=BM ( 根据: )
∵AM=BM ∴CD⊥AB ( 根据: )
2. 切线的判定定理:
经过 并且 的直线是圆的切线.(记住)
所以,直线是圆的切线必须满足(1) ;
(2) .
几何语言:直线经过⊙O的半径OA的外端点A , 且.
∴直线是⊙O的 .(根据 )
3. 切线的性质定理:圆的切线
几何语言为:∵ AB为⊙O的切线,切点为C
∴ AB⊥OC ( )
二、基础应用:
1.(04河北)如图1,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为 .
2.(06河北)如图2,PA是⊙O的切线,切点为A,PA=,∠APO=30°,则⊙O的半径长为 .
3.(07河北)图3中,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,
BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为 .
4.(08河北)如图4,与相切于点,的延长线交于点,连结.若
,则.
5如图,在直径AB=12的⊙O中,弦CD⊥AB于M,
且M是半径OB的中点,则弦CD的长 (保留根号)
6.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,
交⊙O于点C,且CD=l,则弦AB的长是 .
7.如图,AB为⊙O的弦,⊙O的直径为10,OC⊥AB于点D,
交⊙O于点C,且AB=8,则CD的长是 .
三、能力提升:
1.(04河北中考)如图1,一个圆球放置在V形架中.图2是它的平面示意图,CA和CB都是⊙O的切线,切点分别是A,B.如果⊙O的半径为cm,且AB=6cm,求∠ACB.
2.(05河北)工人师傅为了检测该厂生产的一 ( http: / / www.21cnjy.com )种铁球的大小是否符合要求,设计了一个如图1所示的工件槽,其中工件槽的两个底角均为90°,尺寸如图(单位:cm)
将形状规则的铁球放入槽内时,若同时具有图1所示的A,B,E三个接触点,该球的大小就符合要求。
图2是过球心O及A,B,E ( http: / / www.21cnjy.com )三个接触点的截面示意图。已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD,BD⊥CD。请你结合图1中的数据。计算这种铁球的直径。
24.2.5切线长定理
班级: 姓名: 学号:
学习目标:1.知道什么是切线长.2.记住并会用切线长定理
一、学一学:
1.如图1,若AC为⊙O的切线,切点为C,则 ⊥ .
( 根据 )
若∠A=30°,半径为3cm,则线段AC= .
2.切线长:经过圆外一点做圆的切线,这点和切点之间的线段长
叫做这点到圆的切线长. 则图1中的切线长为 cm.
3.探究:如图2所示,PA、PB分别为⊙O的两条切线,切点分别为A、B.
(1)请你通过测量PA、PB的长度,猜想PA与PB满足的数量关系是PA PB;
(2)测量与的度数,猜想与大小关系是 .
并证明你的上述两猜想.
应用:
二、巩固应用:
类型一 利用切线长定理进行计算:
如图,PA、PB分别切⊙O于点A、B,劣弧AB的度数为1200(即所对
的圆心角度数)则∠APB= ,∠APO= ,∠ACB= ;
又知PA=6,则PB= ,圆的半径为 ,弦AB的长度为 .
2.如图,PA、PB、CD分别切⊙O于点A、B、E,请你找出图中
的等线段 、 、 .
若PA=6则△PDC的周长为 .
若∠P=600,⊙O的半径为2,则∠COD= ,△PDC的周长为 .
若点E为劣弧AB上一动点,过点E的⊙O的切线始终与AP,BP交
于点C、D,则△PDC的周长有无变化?为什么?
3. 如图,过半径为6c ( http: / / www.21cnjy.com )m的⊙O外一点P引圆的切线PA、PB,连结PO交⊙O于点F,过F作⊙O的切线分别交PA、PB于D、E,若PO=10cm,∠APB=40°.
(1)求△PED的周长 (2)求∠DOE的度数
类型二 利用切线长定理进行证明:
4.已知:如图,中,,O是AB上一点,以O为圆心,OB为半径的圆与AB交与点E,与AC相切于点D,求证:∥OC
检测A卷 姓名 检测B卷 姓名
1.如图:AE、AD、BC分别切⊙O于E、D、F. 1.如图:AE、AD、BC分别切⊙O于E、D、F
若,则的周长为 . 若,则的周长为 .
2.如图:⊙O 是ABC的内切圆,若∠ ( http: / / www.21cnjy.com )DEF=54° 2.如图:⊙O 是ABC的内切圆,若∠DEF=55°则BAC= ° 则BAC= °
24.2.6圆和圆的位置关系
班级: 姓名: 学号:
一、探索发现
1.观察与思考
下图是两个半径不同的⊙O1和⊙O2,从 ( http: / / www.21cnjy.com )左向右移动⊙O1,你能发现在移动过程中,⊙O1和⊙O2有这5种不同的位置,请你填出每种位置关系时,两圆的交点个数.
交点个数:
2.学一学
(1)如果两个圆没有公共点,那么就说这两 ( http: / / www.21cnjy.com )个圆相离,如图 和 ,相离又分为外离(即一个圆在另一个圆的外部)和内含(即一个圆在另一个圆的内部). 则上图中表示外离的是图 ,表示内含的是图 .
(2)如果两个圆只有一个公共点,那么就说这两个圆相切,如图 和 ,
相切又分为内切和外切.则上图中表示内切的是图 ,表示外切的是图 .
(3)如果两个圆有两个公共点,那么就说这两个圆 .
3.探究 用数量关系识别两圆的位置关系.
设两圆的半径分别为R、r(R>r),圆心距(两圆圆心的距离)为.
二、拓展应用:
类型一:判断两圆的位置关系
1.已知平面内两圆的半径分别为4和6,圆心距是2,则两圆的位置关系是 .
2.已知⊙O1和⊙O2的半径分别为2cm和5cm,且O1O2=6 cm,则⊙O1和⊙O2的位置关系是 .
3. 已知⊙O1和⊙O2的半径分别为3cm和7cm,且O1O2=10cm,则⊙O1和⊙O2的位置关系是 .
4.两圆的半径分别是4cm和3cm,圆心距为1cm,则两圆的位置关系是 ;
5.已知⊙O1和⊙O2的半径分别为R、r, O1O2=5cm,,R=3,当0类型二:根据两圆的位置关系求圆的半径或圆心距.(要注意分类讨论)
1. 有两个圆,一个圆的半径R=4,两圆的圆心距是5,另一个圆的半径r满足条件 时,这两个圆外离.
2.两圆的圆心距为2cm,一个圆的半径为10cm,要使这两个圆内含,另一个圆的半径r应满足条件
3. 半径为1和5的两圆相交,则圆心距d的取值范围为 ;
4. 已知两圆的直径分别为4和6,且这两个圆有唯一公共点,则圆心距d为
5. 已知两圆半径之比为1:2,当两圆相切时,圆心距为8 ,则大圆半径为 ;
6. ⊙O的半径为2,点P是⊙O外一点,OP的长为3,则以点P为圆心,且与⊙O相切的圆的半径为 .
7. 已知两圆内切,圆心距为2cm,如果一个圆的半径是3cm,则另一个圆的半径为 .
8. 相切两圆的圆心距为5,其中一个圆的半径为3,则另一个圆的半径为 .
9. 已知⊙O的半径为5cm,点P是⊙O外一点,OP=8cm,以P为圆心作⊙P与⊙O相切,求⊙P的半径.(写出过程,要考虑全面)
检测A卷 姓名 检测B卷 姓名
1.已知⊙O1和⊙O2的半径分别为3 ( http: / / www.21cnjy.com )cm和7cm, 1.已知⊙O1和⊙O2的半径分别为4cm和6cm,且O1O2=6 cm,则⊙O1和⊙O2的位置关系是 . 且O1O2=6 cm,则⊙O1和⊙O2的位置关系是 .
2.已知两圆的直径分别为6和8,且这两个圆 2.已知两圆的直径分别为10和4,且这两个圆
有唯一公共点,则圆心距d为 有唯一公共点,则圆心距d为
24.3.1正多边形和圆
学习目标:1.知道正多边形的相关概念 2.会解决正多边形问题.
一.忆一忆:
正三角形 正方形 正五边形 正六边形 … 正n边形
内角和 …
每一个内角 …
二.学一学:
2.如图:有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积.
三.练一练:根据表中提供的数值,把其它数据补充完整(正六边形可用上图分析).
四、拓展应用:
1.如图:要拧开一个边长a=12cm的六角形螺帽,扳手张开口b至少要多少?
2.如图,梯形ABCD的四条边都与⊙O相切,切点分别为E、F、G、H.
(1)请你探索AD+BC与AB+CD之间的数量关系.
(2)请你探索DO与CO的位置关系.
(3)若梯形ABCD不是梯形,结论(1)和(2)是否成立,
若成立请给出证明,不成立说明理由.
检测A卷 姓名 检测B卷 姓名
1.边长为的正六边形的一边所对的圆周角 1.边长为的正六边形的一边所对的圆周角
等于 °;面积为 等于 °;面积为
2.如图,点M、N分别是正八边形一组临边 2.如图,点M、N分别是正十边形一组临边
AB、BC上的点,且AM=BN,点O是正八边形 AB、BC上的点,且AM=BN,点O是正十边形
的中心,则∠MON= °. 的中心,则∠MON= °.
24.3.2三角形内切圆
班级: 姓名: 学号:
学习目标:1.知道什么是三角形的内切圆.
2.会解决与三角形的内切圆有关的问题.
一、忆一忆:
1.画出同时经过点A、B、C的⊙O.
2.经过三角形的三个顶点可以作 ( http: / / www.21cnjy.com )圆,这个圆叫做三角形的 ,三角形叫作圆的 ,外接圆的圆心是三角形 的交点,叫做这个三角形的 心.
三角形的外心到三角形 相等.
eq \o\ac(○,3)锐角三角形的外心在三角形的 ( http: / / www.21cnjy.com ) ,直角三角形的外心在三角形的 ,钝角三角形的外心在三角形的 .
任何三角形都有 个外接圆,圆有 个内接三角形.
二、学一学:
1.已知,如图1,⊙O与△ABC的三边分别相切于点D、E、F.
圆心O到三角形三边的距离 ,因为:
圆心O是三角形的 的交点,根据
2.画出下列锐角三角形、直角三角形和钝角三角形的内切圆.
3. 画出⊙O的外切三角形,看能画几个?
三、巩固应用:
1. 如图,O是△ABC的内心.(1) ( http: / / www.21cnjy.com )若∠ABC=500,∠ACB=700,则∠O= ,(2)若∠A=800,则∠O= ,(3)若∠O=1300,则∠A= .
2. 如图,△ABC内接于⊙O,I是△ABC的内心,∠BIC=1300,则∠A ,∠BOC= .∠OBC= .
3. 直角三角形两直角边长分别为5和12,求其内切圆的半径和外接圆的半径为.
4.如图,⊙O切△ABC的三边于点E、F、 G,若AB=9,BC=10,AC=6,求AG、GC、BF的长.
四、知识超市:
5.Rt△ABC中,∠ACB=900,AC=9,BC=24,⊙O为其内切圆,则∠AOB= ,
⊙O的半径为 ,其外接圆的半径为 .
6.正三角形内切圆半径为1,那么这个三角形的边长为
7.如图,点I是△ABC的内心,∠A=800,则∠BIC的度数为 .
8.如图,⊙O是△ABC的内切圆,H为⊙O上任意点,MN切⊙O于H,交AB、AC于点M、N,已
知△ABC的周长为20cm,BC=6cm.则△AMN的周长为
五、能力提升:
在Rt△ABC中,斜边AB=10cm,其内切圆半径为2cm,
则△ABC的面积为 .
检测A卷 姓名 检测B卷 姓名
1. 如图,点O是△ABC的内心,∠BOC =120°, 1. 如图,点O是△ABC的内心,∠BOC =130°,
则∠A的度数为 . 则∠A的度数为 .
2.已知三角形三边长分别为3 , 4 , 5,则它的 2.已知三角形三边长分别为6 , 8 , 10,则它的 内切圆半径为 内切圆半径为
外接圆半径为 外接圆半径为
24.4.1弧长公式扇形面积
班级: 姓名: 学号:
学习目标:记住并会用弧长公式.
一、探究:弧长公式
如右图,在半径为R的圆中,圆的周长.因为的圆心角所对的弧长就是圆的周长,所以的圆心角所对的扇形MON弧长 . 的圆心角所对的扇形AOB弧长.即弧长的计算公式是 .
二、利用弧长公式求弧长、圆心角度数、及圆的半径.
1.一条弧所对的圆心角为90°,半径为3,则这条弧长为 。
2.若一条弧长为72,圆心角为36°,则半径为 。
3.若一条弧长为240,半径为180,则圆心角为 。
4.在半径为3的⊙O中,弦AB=3,则的长为 。
5.如图,∠AOB=90°∠B=20°,以点O为圆心,OA长为半径的圆交AB于点C,若AO=12则的长为 .
6.时钟的轴心到分针针端的长为,那么经过40分钟,分针针端转过的弧长是 .
三、能力提升.
7.如图1…3是边长大于2的 ( http: / / www.21cnjy.com )三角形、四边形、…、凸n边形.分别以它们的个顶点为圆心,以1为半径画弧与相邻边相交,得到3条弧、4条弧、…、n条弧.
(1)图1中的3条弧的弧长的和为 ,图2中的4条弧的弧长的和为
(3)图3中n条弧的弧长的和为 (用含n的式子表示).
检测A卷 姓名 检测B卷 姓名
1.一条弧所对的圆心角为80°,半径为6, 1.一条弧所对的圆心角为60°,半径为6,
则这条弧长为 。 则这条弧长为 。
2.若一条弧长为12,圆心角为120°, 若一条弧长为14,圆心角为120°,
则半径为 。 则半径为 。
24.4.1弧长专练
班级: 姓名: 学号:
学习目标:记住并会用弧长公式.
1.(05咸阳)如图2所示,一条公路的转弯处是一段圆弧(圆中的弧AB),点O是这段弧的圆心,AB﹦120m,OA﹦120m则这段弯路AB长为 m(保留).
2.(07兰州)如图3-1所示,小丽自 ( http: / / www.21cnjy.com )己动手做了一顶圆锥形的圣诞帽,母线长30cm,底面半径10cm,她想在帽子上缠一根漂亮的丝带,从点A出发绕帽子侧面一周,至少需丝带
3.(05内江)如图4-1,有一圆锥形 ( http: / / www.21cnjy.com )粮堆,其主视图是边长为6m的正三角形ABC,母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是 m(结果不取近似数).
4.(06株州)我国南方一些地区的农民戴 ( http: / / www.21cnjy.com )的斗笠是圆锥形.已知圆锥的母线长为30 cm,底面圆的半径为24 cm,则圆锥侧面积为 cm2.
5.(05河南)图7-1、7-2是用两种方法 ( http: / / www.21cnjy.com )把6根圆形钢管用钢丝绳捆扎的截面图.设7-1、7-2两种方法捆扎所需钢丝绳的长度分别为a、b(不计接头部分)则a、b的大小关系为a b.
6.06山西)图8是某圆柱形网球筒,其底面直径是10cm,长
为80cm,将七个这样的网球筒如图所示放置并包装侧面,则需
________________的包装膜(不计接缝,π取3)。
7.(2010 嵊州市)如图9,是7根圆柱形木棒的横截面圆的半径均
为1,则捆扎这7根木棒一周的绳子长度为 。
8.(06河南)如图10,一块含有30°角的直角三角板ABC,
在水平桌面上绕点C按顺时针方向旋转到的位置,若
BC的长为15 cm,那么顶点A从开始到结束所经过的路径长为____________
9.(06济南)如图11,矩形ABC ( http: / / www.21cnjy.com )D中,AB=8,AD=6,将矩形ABCD在直线上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
10.(07台湾)如图(12-1),水平地面上有一面积为30 平方公分的灰色扇形OAB,其中的长度为6公分,且与地面垂直。若在没有滑动的情况下,将图(12-1)的扇形向右滚动至垂直地面为止,如图(12-2)所示,则O点移动 公分.
24.4.2扇形面积
学习目标:记住并会用扇形面积.
一、探究:扇形面积
如图,在半径为R圆中,因为的圆心角所对的扇形面积就是圆的
面积 , 所以的圆心角所对的扇形面积
所以圆心角是扇形面积.
二、利用扇形面积计算公式进行计算
1.一扇形半径为60cm, 圆心角为150°,则扇形的面积是 .
2.一扇形的弧长为20 cm ,面积为 240cm2 ,,则扇形的圆心角是 .
3.如图所示,一扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°AB=30cm
贴纸部分BD长为20cm,则贴纸部分的面积为 .
4.(08南昌)如图,为的直径,于点,交于点,于点.(1)请写出三条与有关的正确结论;
(2)当,时,求圆中阴影部分的面积.
能力提升:
1.如图,⊙A,⊙B,⊙C两两不相交,且半径都是0.5cm,
则图中的三个扇形(即阴影部分)的面积 .
2.如图A是半径为2的⊙O外一点,OA=4,
AB是⊙O的切线,点B是切点,BC∥OA,
连接AC,则阴影部分的面积等于
扇形面积专练
学习目标:记住并会用扇形面积.
1.(05年·江苏)如图所示,Rt△A ( http: / / www.21cnjy.com )BC的面积为20cm2,在AB的同侧,分别以AB、BC、AC为直径作三个半圆,阴影部分的面积 .
2.(2010云南昆明)如图,在△ABC ( http: / / www.21cnjy.com )中,AB = AC,AB = 8,BC = 12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是
3.(2010湖南衡阳)如图,在R ( http: / / www.21cnjy.com )t△ABC中,∠C=90°,AC=4,BC=2分别以AC、BC为直径画半圆,则图中阴影部分的面积为 .(结果保留π)
4.(2010山东临沂) 如图,直径为6的半径,绕点逆时针旋转60°,此时点到了点,则图中阴影部分的面积是
5.如图,△ABC是正三角形,曲线CDEF…叫做“正三角形的渐开线”,其中弧、、、的圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则
曲线CD的长;曲线DE的长;曲线EF的长为第n段曲线的长;则
;则
6.(2010湖北黄石)如图,从一个 ( http: / / www.21cnjy.com )直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为
24.4.3圆锥的侧面展开图
学习目标:会计算圆锥的侧面积和全面积.
一、学一学:
1.圆锥的母线:我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.如图中.
2.圆锥的高:连接顶点和底面圆心的线段叫做圆锥的高. 如图中h就是圆锥的高.
二、探究与思考:
如图,圆锥是由一个底面和一个侧面围成的,沿圆锥的一条母线将圆锥侧面剪开并展平,可以得到圆锥的侧面展开图是一个扇形,设圆锥的母线长为,底面圆的半径为r,那么侧面展开图扇形的半径为圆锥的母线长,扇形的弧长(即底面圆的周长)为 ,由扇形的面积公式可得圆锥侧面展开图的面积为= ,圆锥的底面积为 ,圆锥的全面积为 .(圆锥的全面积=侧面积+底面积).
三、巩固应用:
1.已知圆锥的底面半径为80cm,母线长90cm,则它的侧面积为 ,全面积为
侧面展开图圆心角的度数为 .
2.已知圆锥的底面半径为3,高为4,则这个圆锥的母线长为 ,侧面积为 .
3.圆柱的高为20cm,底面半径是高的,那么圆柱的侧面积为 。
4. 若圆锥的母线长为6cm,侧面展开图的圆心角为的扇形,则圆锥底面半径为 cm.
5.若用半径为15cm,圆心角为的扇形围成一个圆锥的侧面,这个圆锥的高为 cm.
6.圆锥的侧面积为,母线长为3,侧面展开图(扇形)的圆心角为
四、中考真题回放
1.(2003,河北)已知圆锥的底面直径为4,母线长为6,则它的侧面积为 。
2.(2004河北)如图1,在正方形铁 ( http: / / www.21cnjy.com )皮上剪下一个圆形和扇形,使之恰好围成图3—2所示的一个圆锥模型.设圆的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为( )
A.R=2r B.R=r
C.R=3r D.R=4r
3.(04河北)图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽的纸的面积为 cm2
(π取3.14).
4. (05河北)如图3,已 ( http: / / www.21cnjy.com )知圆锥的母线长OA=8,底面圆的半径为r=2,若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线长为
(结果保留跟号)
5.(09,唐山模拟)如图 ( http: / / www.21cnjy.com )1,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.测量出AD所对的圆心角为120°,如图2所示.
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留 和根号)
《弧长、扇形等面积》
学习目标:会计算弧长和扇形面积
1.已知扇形的圆心角为,半径为2cm,则扇形的弧长是 cm,扇形的面积是____ .
2. (2006 梅州课改)如图,两个半圆中,小圆的圆心在大的直径上,长为4的弦与直径平行且与小半圆相切,那么圆中阴影部分面积等于 .
3.如图,一块含有角的直角三角板,在水平桌面上绕点按顺时针方向旋转到的位置.若的长为,那么顶点从开始到结束所经过的路径长为 .
4.如图,的边长都大于2,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形的相邻两边上),则这三条弧的长的和是 .
5.如图,,,,相互外离,它们的半径都是,顺次连结四个圆心得到四边形,则图中四个扇形(阴影部分)的面积之和等于__________.(结果保留)
6.如图,,为的中点,都是半径为3的的切线,为切点,则的长为 .
7.将边长为8cm的正方形的四边沿直线向右滚动(不滑动),当正方形滚动两周时,正方形的顶点所经过的路线的长是 cm.
8.如图,的半径为3,,切于,弦,连结,图中阴影部分的面积为 .
9.如图,有一圆锥形粮堆,其正视图是边长为 ( http: / / www.21cnjy.com )6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是______m(结果不取近似值).
10.(2005年成都市)农村常搭建橫截面为 ( http: / / www.21cnjy.com )半圆形的全封闭塑料薄膜蔬菜大棚,如图所示,如果不考虑塑料薄膜接头重合及埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是 .
11.图10—1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图10—2是车棚顶部截面的示意图,所在圆的圆心为O.
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留).
圆(单元论坛)
圆的有关性质
1.圆是 轴对称图形, 的直线都是它的对称轴,有 条对称轴,圆
是中心对称图形,又是旋转对称图形,即旋转任意角度都和自身重合. 对称中心.
2.外心—是三角形 的圆心 到三角形 的距离相等.
(是 的交点)
内心—是三角形 的圆心 到三角形 的距离相等.
3. 垂径定理及推论:
如图:AB是⊙O的直径,CD是弦。
(1)若AB⊥CD 则有 PC=PD且 =
根据:
(2)若PC=PD 则有 AB⊥CD 且 =
根据:
垂径定理
1、已知OC⊥AB 2、已知弦AB= 3、已知⊙O半径2 4、已知直径AB⊥CD,
OC=3,AB=8 ∠AOB=120° 弦AB= BE=1,弦CD=10
则⊙O半径 则⊙O半径 则∠AOB= 则⊙O半径
圆心角、弧、弦之间的关系:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等它们所对应的其余各组量分别 .
如图,若∠AOB=∠BOC则有 , .
圆心角和圆周角的关系:
的角叫圆心角;
角叫圆周角.
(2)一条弧所对的圆周角等于它所的圆心角的 ,在同圆或等圆中,同弧或等弧所对的圆周角 ,直径所对的圆周角是 ,的圆周角所对的弦是 .
①若则 . ②若则
③若 AB是⊙O的直径,则∠ACB= ④若∠ACB是直角,则弦AB是
点和圆的位置关系:
设圆的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在圆外d r; (2) 点P在圆上d r; (3)点P在圆内d r;
6.直线和圆的位置关系:
设⊙O的半径为r,圆心O到直线的的距离为d,则有:
直线与⊙O相离 ; 直线与⊙O相切 ;直线与⊙O相交 .
7.圆和圆的位置关系:
设两圆的半径分别为R、r(R>r),圆心距(两圆圆心的距离)为
(1)两圆外离;(2)两圆外切 ;(3)两圆相交 <<
(4)两圆内切 ;(5)两圆内含 .(记住上述数量关系)
练一练:
①已知平面内两圆的半径分别为4和6,圆心距是2,则两圆的位置关系是 .
②已知⊙和⊙的半径分别为2cm和5cm,且,则⊙和⊙的位置关系是 .若两圆相切,则圆心距为 .
③已知⊙和⊙的半径分别为3cm和7cm,且,则⊙和⊙的位置关系是 .
④两圆的半径分别是4cm和3cm,圆心距为1cm,则两圆的位置关系是 ;
⑤已知⊙和⊙的半径分别为R、r,R=3,当时,则⊙和⊙的位置关系是 .
8.切线的判定和性质:
切线的判定:
①到圆心的距离等于半径的直线是圆的 ;
②经过半径的外端并且 这条半径的直线是圆的切线.
(2)切线的性质:圆的切线 经过切点的半径.
①如图①所示,PA为⊙O的切线,切点为A, PA=, 则⊙O的半径为
②如图②AB与⊙O相切于点B,AO的延长线交⊙O于点C, 连接BC,若,则
③如图③AB与⊙O相切于点A,BO交⊙O于点C, ,则
④已知直线CD与⊙O相切于C,AB为直径,若,则大小为
9.圆的有关计算:
(1)弧长 .
①一条弧所对的圆心角为90°,半径为3,则这条弧长为 。
②若一条弧长为72,圆心角为36°,则半径为 。
③若一条弧长为240,半径为180,则圆心角为 。
(2)扇形面积:S= 或S=
①一扇形半径为60cm, 圆心角为150°,则扇形的面积是 .
②一扇形的弧长为20 cm ,面积为 240cm2 ,,则扇形的圆心角是 (3)圆锥:①圆锥的侧面展开图是一个 。圆锥的母线 扇形半径R.
圆锥的底面圆周长 扇形弧长.
②圆锥的侧面积等于设圆锥的母线长为,底面圆的半径为r,则它的侧面积为 . + .(记住会用)
跟踪训练:
①已知圆锥的底面半径为80cm,母线长90cm,则它的侧面积为 ,全面积为
侧面展开图圆心角的度数为 .
②已知圆锥的底面半径为6,高为8,则这个圆锥的母线长为 ,侧面积为 .
③圆柱的高为40cm,底面半径是高的,那么圆柱的侧面积为 。
④若圆锥的母线长为6cm,侧面展开图的圆心角为的扇形,则圆锥底面半径为 cm.
24.2.1点和圆的位置关系
【自主学习】
(一)复习巩固:
1.已知AB是⊙O的直径,C是⊙O上一点,若AB=4cm,AC=3cm,则BC= .
2.下列命题:①直径所对的角 ( http: / / www.21cnjy.com )是900 ;②直角所对的弦是直径;③相等的圆周角所对的弧相等;④对同一弦的两个圆周角相等.正确的有( )A. 0个 B. 1个 C.2个 D.3个
(二)新知导学
1.过不在同一直线上的三个点确定 圆.
2.经过三角形的三个顶点的圆叫做三角形的 ,外接圆的圆心叫做三角形的 ,
这个三角形叫圆的 三角形.
【合作探究】
要将如图所示的破圆轮残片复制完成,
怎样确定这个圆轮残片的圆心和半径
(写出找圆心和半径的步骤).
【自我检测】
一、填空题:
1.锐角三角形的外心在_______.如果一个三角形的外心在它的一边的中点上, 则该三角形是______.如果一个三角形的外心在它的外部,则该三角形是_____.
2.边长为6cm的等边三角形的外接圆半径是________.
3.△ABC的三边为2,3, ,设其外心为O,三条高的交点为H,则OH的长为_____.
4.三角形的外心是______的圆心,它是_______的交点,它到_______的距离相等.
5.已知⊙O的直径为2,则⊙O的内接正三角形的边长为_______.
6.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用________ 次就可以找到圆形工件的圆心.
二、选择题:
7.下列条件,可以画出圆的是( )
A.已知圆心 B.已知半径;
C.已知不在同一直线上的三点 D.已知直径
8.三角形的外心是( )
A.三条中线的交点; B.三条边的中垂线的交点;
C.三条高的交点; D.三条角平分线的交点
9.下列命题不正确的是( )
A.三点确定一个圆 B.三角形的外接圆有且只有一个
C.经过一点有无数个圆 D.经过两点有无数个圆
10.一个三角形的外心在它的内部,则这个三角形一定是( )
A.等腰三角形 B.直角三角形; C.锐角三角形 D.等边三角形
11.等腰直角三角形的外接圆半径等于( )
A.腰长 B.腰长的倍; C.底边的倍 D.腰上的高
12.平面上不共线的四点,可以确定圆的个数为( )
A.1个或3个 B.3个或4个 C.1个或3个或4个 D.1个或2个或3个或4个
三、解答题:
13.如图,A、B、C三点表示三个工厂,要 ( http: / / www.21cnjy.com )建立一个供水站, 使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).
14.如图,已知△ABC的一个外角∠C ( http: / / www.21cnjy.com )AM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.(1)判断△FBC的形状,并说明理由.
(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,
并说明你给出的等式成立.
15.如图,在钝角△ABC中,AD ( http: / / www.21cnjy.com )⊥BC,垂足为D点,且AD与DC的长度为x2-7x+12=0的两个根(AD16.已知△ABC内接于⊙O,OD⊥BC,垂足为D,若BC=2,OD=1,求∠BAC的度数.(注意:分类讨论)
24.2.2直线和圆的位置关系(1)
新知导学
1.直线与圆的位置关系
①定义:直线与圆有 个公共点时,叫做直线与圆相交,这条直线叫做圆的 线.
直线与圆有 个公共点时,叫做直线与圆相切,这条直线叫做圆的 线.这个公
共点叫做 点.直线与圆有 个公共点时,叫做直线与圆相离.
直线与圆的位置关系的性质与判定
设⊙O的半径为r,圆心O到直线的距离为d,那么
直线与圆相交 ;
直线与圆相切 ;
直线与圆相离 .
【合作探究】
1.在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有交点,试确定r的范围.
【自我检测】
一、选择题
1.命题:“圆的切线垂直于经过切点的半径”的逆命题是( )
A.经过半径的外端点的直线是圆的切线.B.垂直于经过切点的半径的直线是圆的切线.
C.垂直于半径的直线是圆的切线. D.经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.如图,AB、AC与⊙O相切于 ( http: / / www.21cnjy.com )B、C,∠A=500,点P是圆上异于B、C的一个动点,则∠BPC的度数是( )A.650 B.1150 C.650或1150 D.1300或500
3.已知正三角形的边长为6,则该三角形外接圆的半径为( )
A. B.3 C. D.1
4.如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,如果PA=,OB=1,那么∠APC等于( )A. 150 B.300 C.450 D.600
5.如图,线段AB经过圆心O,交⊙O于 ( http: / / www.21cnjy.com )点A、C,∠B=300,直线BD与⊙O切于点D,则∠ADB的度数是( )A.1500 B.1350 C.1200 D.1000
6.在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( )
A. x轴相交 B. y轴相交 C. x轴相切 D. y轴相切
7.如图,⊙的直径与弦的夹角为,切线与的延长线交于点,若⊙的半径为3,则的长为( )A.6 B. C. 3 D.
二、填空题
8.如图,已知直线CD与⊙O相切于点C,AB为直径,若∠BCD=40°,则∠ABC的大小等于_____.
9.如图,PA是⊙O的切线,切点为A,PA=,∠APO=30°,则⊙O的半径长为_______.
10.如图,图同第7题,AB是⊙O的直径,BD=OB,∠CAB=300.,写出三个正确结论
(除AO=OB=BD外):①___ ( http: / / www.21cnjy.com )_________________;②____________________;③____________________.
11.已知∠AOB=300,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M. 当OM=_______cm时,⊙M与OA相切(如图).
12.如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过
点D作DE⊥AC,垂足为E. 根据以上条件写出三个正确的结论(除AB=AC,AO=BO, ABC=∠ABC外)是:
(1) ___________________;(2) ___________________;(3) __________________
三、解答题
13.如图,∠PAQ是直角,⊙O 与AP相切于点T,与AQ交于B、C两点.
(1)BT是否平分∠OBA?说明你的理由;
(2) 若已知AT=4,弦BC=6,试求⊙O 的半径R.
14.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC.
(1) 求证:△BAD∽△CED; (2) 求证:DE是⊙O的切线.
24.2.2直线和圆的位置关系(2)
新知导学
1.切线的判定定理:经过半径的 并且 这条半径的直线是圆的切线.
2.切线的性质定理:圆的切线 于经过切点的 .
3.与三角形各边都 的圆叫做三角形的 圆, 圆的
叫做三角形的 ,这个三角形叫做圆的 三角形.
【合作探究】
如图,AB、CD分别与半圆O切于点A、D,BC切⊙O于点E,若AB=4,CD=9,
求⊙O的半径.
2.已知锐角△ABC,作△ABC的内切圆.
【自我检测】
一、选择题
1.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论错误的是( )
A. ∠1=∠2 B.PA=PB C.AB⊥OP D.
2.如图,⊙O内切于△ABC,切点为D ( http: / / www.21cnjy.com )、E、F,若∠B=500,∠C=600,连结OE、OF、DE、DF,则∠EDF等于( )A.450 B.550 C.650 D.700
3.边长分别为3、4、5的三角形的内切圆与外接圆半径之比为( )
A.1:5 B.2:5 C.3:5 D.4:5
4.如图,PA、PB是⊙O的两条切线,切点是A、B. 如果OP=4,,那么∠AOB等于( )A. 90° B. 100° C. 110° D. 120°
5.如图,已知⊙O过边长为正2的方形ABCD的顶点A、B,且与CD边相切,则圆的半径为( )A. B. C. D.1
6.如图,⊙O为△ABC的内切圆,∠C=900,AO的延长线交BC于点D,AC=4,CD=1,
则⊙O的半径等于( )A. B. C. D.
1题图 2题图 4题图
二填空题
7. 直角三角形有两条边是2,则其内切圆的半径是__________.
8. 正三角形的内切圆半径等于外接圆半径的__________倍.
9.如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠BAC=200,则∠P的大小是___度.
10.等边三角形ABC的内切圆面积为9π,则△ABC的周长为_________.
11.已知三角形的三边分别为3、4、5,则这个三角形的内切圆半径是 .
12.三角形的周长是12,面积是18,那么这个三角形的内切圆半径是 .
三、解答题:
13.已知如图,过圆O外 ( http: / / www.21cnjy.com )一点B作圆O的切线BM, M为切点.BO交圆O于点A,过点A作BO的垂线,交BM于点P.BO=3,圆O半径为1.求MP的长.
14.如图,AB是半圆O的直径,点 ( http: / / www.21cnjy.com )M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.(1) 当∠PQA=600时,请你对△QCP的形状做出猜想,并给予证明;
(2) 当QP⊥AB时,△QCP的形状是__________三角形;
(3) 由(1)、(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时, △QCP一定是_________三角形.
15.已知:∠MAN=30°,O为边AN上一点,以O为圆心、2为半径作⊙O ,交AN于D、E两点,设AD=.
⑴ 如图⑴当取何值时,⊙O与AM相切;
⑵ 如图⑵当为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
24.2.3 圆和圆的位置关系
(一)复习巩固:
1圆的切线的性质定理: .
2.圆的切线的判定定理: .
3.三角形的内心是它的 圆的圆心,它是三角形 的交点.
4.内心到三角形 的距离相等,到三角形三边距离相等的点是 .
5.已知三角形的面积为12,周长为24,则内切圆的半径为 .
(二)新知导学
圆与圆的五种位置关系的性质与判定
如果两圆的半径为R、r,圆心距为d,那么
两圆外离 ;两圆外切 ;
两圆相交 ;两圆内切 ;
两圆内含 .
(位置关系) (数量关系)
【合作探究】
1.已知两圆相切,一个圆的半径为5,圆心距d=2,求另一个圆的半径.
2.半径为1、2、3的三个圆两两外切,求这三个圆的圆心的连线构成的三角形的面积.
【自我检测】
一、填空题:
1.已知两圆半径分别为8、6,若两圆内切,则圆心距为______;若两圆外切,则圆心距为___.
2.已知两圆的圆心距d=8,两圆的半径长是方程x2-8x+1=0的两根,则这两圆的位置关系是______.
3.圆心都在y轴上的两圆 ( http: / / www.21cnjy.com )⊙O1、⊙O2,⊙O1的半径为5,⊙O2的半径为1,O1 的坐标为(0,-1),O2的坐标为(0,3),则两圆⊙O1与⊙O2的位置关系是________.
4.⊙O1和⊙O2交于A、B两点,且⊙O1经过点O2,若∠AO1B=90°,那么∠AO2B 的度数是__.
5.矩形ABCD中,AB=5,BC ( http: / / www.21cnjy.com )=12,如果分别以A、C为圆心的两圆相切,点D在⊙C内, 点B在⊙C外,那么圆A的半径r的取值范围是__________.
6.两圆半径长分别是R和r(R> ( http: / / www.21cnjy.com )r),圆心距为d,若关于x的方程x2-2rx+(R-d)2=0 有相等的两实数根,则两圆的位置关系是_________.
二、选择题
7.⊙O的半径为2,点P是⊙O外一 ( http: / / www.21cnjy.com )点,OP的长为3,那么以P为圆心,且与⊙O 相切的圆的半径一定是( ) A.1或5 B.1 C.5 D.1或4
8.直径为6和10的两上圆相外切,则其圆心距为( ) A.16 B.8 C.4 D.2
9.如图1,在以O为圆心的 ( http: / / www.21cnjy.com )两个圆中,大圆的半径为5,小圆的半径为3, 则与小圆相切的大圆的弦长为( ) A.4 B.6 C.8 D.10
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
10.⊙O1、⊙O2、⊙O3两两外切,且半径分别为2cm,3cm,10cm,则△O1O2O3 的形状是( )
A.锐角三角形 B.等腰直角三角形; C.钝角三角形 D.直角三角形
11.如图2,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线, 切点为A,则O1A的长为( ) A.2 B.4 C. D.
12.半径为1cm和2cm的两 ( http: / / www.21cnjy.com )个圆外切,那么与这两个圆都相切且半径为3cm 的圆的个数是( ) A.5个 B.4个 C.3个 D.2个
13.如图3,⊙O的半径为r,⊙O1、⊙O2 ( http: / / www.21cnjy.com )的半径均为r1,⊙O1与⊙O内切,沿⊙O 内侧滚动m圈后回到原来的位置,⊙O2与⊙O外切并沿⊙O外侧滚动n圈后回到原来的位置,则m、n的大小关系是( ) A. m>n B. m=n C. m三、解答题
14.若两圆的圆心距d满足等式│d-4│=3,且两圆的半径是方程x2-7x+12=0 的两个根,试判断这两圆的位置关系.
15.某人用如下方法测一钢管的内径: ( http: / / www.21cnjy.com )将一小段钢管竖直放在平台上, 向内放入两个半径为5cm的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD的长.
16.如图,⊙O1、⊙O ( http: / / www.21cnjy.com )2交于A、B两点,点O1在⊙O2上,两圆的连心线交⊙O1于E、D,交⊙O2于F,交AB于C,请根据图中所给的已知条件(不再标注其他字母, 不再添加任何辅助线),写出两个线段之间的关系式.
24.3正多边形和圆
(一)复习巩固
1. 等边三角形的边、角各有什么性质? .
2. 正方形的边、角各有什么性质? .
(二)新知导学
1.各边 ,各角 的多边形是正多边形.
2.正多边形的外接圆(或内切圆)的圆心叫做 ,外接圆的半径叫做 ,
内切圆的半径做 .正多边形各边所对的外接圆的圆心角都 .正多边形每一边所对的外接圆的圆心角叫做 .正n边形的每个中心角都等于 .
3.正多边形都是 对称 ( http: / / www.21cnjy.com )图形,正n边形有 条对称轴;正 数边形是中心对称图形,对称中心就是正多边形的 ,正 数边形既是中心对称图形,又是轴对称图形.
【合作探究】
1.问题:用直尺和圆规作出正方形,正六多边形.
思考:如何作正三角形、正十二边形?
【自我检测】
1.正方形ABCD的外接圆圆心O叫做正方形ABCD的______.
2.正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
3.若正六边形的边长为1,那么正六边形的中心角是______度,半径是______,边心距是______,它的每一个内角是______.
4.正n边形的一个外角度数与它的______角的度数相等.
5.设一直角三角形的面积为8㎝2,两直角边长分别为x㎝和y㎝.
(1)写出y(㎝)和x(㎝)之间的函数关系式
(2)画出这个函数关系所对应的图象(3)根据图象,回答下列问题:
① 当x =2㎝时,y等于多少?
② x为何值时,这个直角三角形是等腰直角三角形?
6.已知三角形的两边长分别是方程 的两根,第三边的长是方程 的根,求这个三角形的周长.
7.如图,PA和PB分别与⊙O相切于A,B两点,作直径AC,并延长交PB于点D.连结OP,CB.
(1)求证:OP∥CB;
(2)若PA=12,DB:DC=2:1,求⊙O的半径.
8.如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0,)两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似.
若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
9.如示意图,小华家(点A处)和公路( ( http: / / www.21cnjy.com ) )之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家岛公路的距离(精确到1m).
24.4.1弧长及扇形面积
(一)复习巩固:
1.圆与圆的五种位置关系: 、 、 、 、 .
2.已知两圆的半径分别3cm和2cm,若两圆没有公共点,则圆心距d的取值范围为( )
A. d>5或d<1 B. d>5 C. d<1 D.1<d<5
(二)新知导学
1.弧长计算公式
在半径为R的圆中,n0的圆心角所对的弧长l的计算公式为: l=
2.扇形面积计算公式
①定义: 叫做扇形.
②在半径为R的圆中,圆心角为n0的扇形面积的计算公式为:S扇形=
由弧长l= 和S扇形= 可得扇形面积计算的另一个公式为:
S扇形=
【合作探究】
1.已知:扇形的弧长为cm,面积为 cm2 ,求扇形弧所对的圆心角.
已知:AC是半圆的直径,BC与半圆切于C,AB交半圆于D,BC=3 cm BD= cm,
求半圆的面积.
【自我检测】
一、选择题
1.如果以扇形的半径为直径作一个圆,这个圆的面积恰好与已知扇形的面积相等,则已知扇形的中心角为( )
A.60° B.90° C.120° D.150°
2.如果圆柱底面直径为6cm,母线长为4cm,那么圆柱的侧面积为( )
A.24πcm2 B.36πcm2 C.12πcm2 D.48πcm2
3.圆锥的母线长为5cm,底面半径为3cm,则圆锥侧面展开图的面积是( )
A. πcm2 B.30πcm2 C.24πcm2 D.15πcm2
4.如果正四边形的边心距为2,那么这个正四边形的外接圆的半径等于( )
A.2 B.4 C. D.
5.圆的外切正六边形边长与它的内接正六边形边长的比为( )
A.:3 B. 2:3 C.3:3 D.:2
6.圆的半径为3cm,圆内接正三角形一边所对的弧长为( )
A.2πcm或4πcm B.2πcm C.4πcm D.6πcm
7.在半径为12cm的圆中,150°的圆心角所对的弧长等于( )
A.24πcm B.12πcm C.10πcm D.5πcm
8.如图, 设AB=1cm,,则长为( )
A. B. C. D.
9.圆锥的母线长为5cm,高为3cm,则其侧面展开图中,扇形的圆心角是( )
A.144° B.150° C.288° D.120°
二、计算题
10.如图,已知菱形ABCD中,AC,BD交于O点,AC=cm,BD=2cm,分别以 A,C为圆心,OA长为半径作弧,交菱形四边于E,F,G,H四点.求阴影部分的面积.
11.已知△ABC中,∠C=90°,AC=3cm,BC=4cm,⊙O内切于△ABC.求△ABC在⊙O外部的面积.
12.已知等腰梯形ABCD有一个内切圆O.若AB=CD=6cm,BC=2AD,求圆O的面积.
13.如图,ACBD为夹在环形的两条半径之间的一部分,弧AD的长为πcm,弧CB的长为2πcm,AC=4cm,求这个图形的面积.
14.已知如图,P是半径为R的⊙O外一 ( http: / / www.21cnjy.com )点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.求:夹在劣弧AB及PA,PB之间的阴影部分的面积.
15.已知扇形OAB的面积为S,∠AOB=60°.求扇形OAB的内切圆的面积.
三、证明
16.如图,已知同心⊙O中,外圆的面积是内圆 ( http: / / www.21cnjy.com )面积的2倍,外圆的弦AB,CD均与内圆相切,且AB∥CD.EFGH是内圆的内接正方形.求该圆环介于AB,CD间的面积等于正方形EFGH的面积.
17.已知直角三角形斜边上的高将原三角形分成两个直角三角形.求证这两个三角形的内切圆的面积的和等于原三角形的内切圆面积.
18.已知如图7-391,AB ( http: / / www.21cnjy.com )是半圆O的直径,C,D是半圆上两点,且弧AC=弧CD=弧DB,求证由弦AC及弧CD所围成的图形面积等于半圆面积的三分之一
19.若分别以线段CD的两个端点为 ( http: / / www.21cnjy.com )圆心,CD长为半径的⊙C,⊙D相交于A,B.求证分别以AB,CD为直径的两个圆的面积之和与⊙C的面积相等.
20.求证圆心角为60°的扇形的内切圆的面积,等于扇形面积的三分之二.
21.已知如图7-392,扇 ( http: / / www.21cnjy.com )形OAB中,OA⊥OB,分别以OA,OB为直径向形内作半圆,两圆弧交于C,求证由弧AC,弧BC,弧AB所围图形的面积与由弧OMC和弧ONC所围图形面积相等.
24.4.2圆锥的侧面积和全面积
【自主学习】
(一)复习巩固:
1.弧长的计算公式: .
2.扇形面积的计算公式: .
3.已知扇形的面积为4cm2,弧长为4cm,求扇形的半径.
(二)新知导学
1.圆锥的侧面展开图
圆锥的侧面展开图是一个 .
圆锥的母线就是扇形的 .
圆锥底面圆的周长就是扇形的 .
2.如果圆锥的母线长为l,底面的半径为r,那么
S侧= ,
S全= .
【合作探究】
1.已知圆锥的母线长6 cm;底面半径为 3 cm,求圆锥的侧面展开图中扇形的圆心角.
2.已知:一个圆锥的侧面展开图是圆心角为36°的扇形,扇形面积为10 cm2.求这圆锥的表面积.
【自我检测】
一、选择题
1.已知圆锥的高为,底面半径为2,则该圆锥侧面展开图的面积是( )
A.π B.2π C.π D.6π
2.圆锥的高为3cm , 母线长为5cm , 则它的表面积是( )cm2.
A.20p B.36p C.16p D.28p
3.已知圆锥的底面半径为3 , 母线长为12 ( http: / / www.21cnjy.com ) , 那么圆锥侧面展开图所成扇形的圆角为( )A.180° B.120° C.90° D.135°
4.如果圆锥的高与底面直径相等 , 则底面面积与侧面积之比为( )
A.1∶ B.2∶ C.∶ D.2∶3
5.边长为a的等边三角形 , 绕它一边上的高所在直线旋转180° , 所得几何体的表面积为( )A. B. C. D.π
6.若底面直径为6cm的圆锥的侧面展开图的圆心角为216°,则这个圆锥的高是( )cm.A.8 B. C.6 D.4
7.在一个边长为4cm正方形里作一个扇形(如图所示) , 再将这个扇形剪下
卷成一个圆锥的侧面 , 则这个圆锥的高为( )cm.
A. B. C. D.
8.用圆心角为120° , 半径为6cm的扇形围成圆锥的侧面 , 则这个圆锥的高为( )A.4 B.4 C.2 D.3
9.△ABC中 , AB=6cm , ∠A ( http: / / www.21cnjy.com )=30° , ∠B=15° , 则△ABC绕直线AC旋转一周所得几何体的表面积为( )cm2.
A.(18+9)π B.18+9
C.(36+18)π D.36+18
10.圆锥的母线长为10cm , 底面半径为3cm , 那么圆锥的侧面积为( )cm2.
A.30 B.30p C.60p D.15p
11.粮仓的顶部是圆锥形,这个圆锥的底面直径是4 m,母线长3 m,为防雨需在粮仓的顶部铺上油毡,那么这块油毡的面积至少为( )
A.6 m2 B.6πm2 C.12 m2 D.12πm2
12.若圆锥的侧面展开图是一个半径为a的半圆,则圆锥的高为( )
A.a B. C. D.
13.一个圆锥的高为cm,侧面展开图是一个半圆,则圆锥的全面积是( )
A.200πcm2 B.300πcm2 C.400πcm2 D.360πcm2
14.一个圆锥形的烟囱帽的侧面积为2000πcm2,母线长为50cm,那么这个烟囱帽的底面直径为( )
A.80cm B.100cm C.40cm D.5cm
二、填空题
15.已知圆锥的母线长是10cm,侧面展开图的面积是60πcm2,则这个圆锥的底面半径
是 cm.
16.已知圆锥的底面半径是2cm,母线长是5cm,则它的侧面积是 .
17.圆锥的轴截面是一个等边三角形,则这个圆锥的底面积、侧面积、全面积的比是 .
18.一个扇形,半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为 .
19.一个扇形,半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,那么这个圆锥的全面积为 .
三、解答题
20.一个圆锥形的零件,经过轴的剖面是一个等腰直角三角形,则它的侧面展开图扇形的圆心角是多少?
21.如图,一个圆柱的底面半径为40 cm,高为60 cm,从中挖去一个以圆柱上底为底、下底圆心为顶点的圆锥,得到一个几何体,求其全面积.
22.已知:一个圆锥的侧面积与表面积的比为2∶3.求这圆锥的锥角.
23.已知:一个圆锥的底半径 r=10cm,过轴的截面的顶角为60°.求它的侧面展开图的圆心角的度数及侧面积.
于是得到切线的性质定理:
圆的切线垂直于经过切点的半径.
几何语言为:∵ BC为⊙O的切线,切点为A
∴ BC⊥OA ( )
C
O
A
B
图4
·
A
B
C
D
O
M
第5题图
A
P
O
图2
A
P
O
图1
B
A
B
C
D
O
图3
E
第6-7题图
图1
图2
A
O
B
C
A
E
B
4
4
16
图1
A
C
E
D
B
O
图2
图1
图2
由此我们可以得到切线长定理:
从圆外一点引圆的两条 ,它们的 相等,这一点和圆心的连线平分两条切线的 .(记住)
几何语言为:∵ PA、PB是⊙O的切线,A、B为切点.
∴PA PB, .
1题图
2题图
3题图
4题图
2题图
; ;
1.悄悄告诉你:
eq \o\ac(○,1)一个正多边形的外接圆(或内切圆)的圆心叫这个正多边形的中心.
eq \o\ac(○,2)一个正多边形的外接圆的半径叫正多边形的半径.
eq \o\ac(○,3)正多边形每一条边所对的圆心角叫做正多边形的中心角.
eq \o\ac(○,4)中心到正多边形一边的距离叫做正多边形的边心距. 边心距也是正多边形内切圆的
2.考考你:
eq \o\ac(○,1)请你指出图中正多边形的中心 ;正多边形的半径 ;正多边形的中心角 ;
正多边形的边心距 ;
eq \o\ac(○,2)正三角形的中心角有 个,中心角的度数为 ;正四边形、正五边形、正六形呢?
……正n边形的中心角有 个,中心角的度数为 .
导学分析:
eq \o\ac(○,1)正六边形的中心角 ,所以 是等边三角形,
OC=OD= = m.所以正六边形的周长为 .
eq \o\ac(○,2)正六边形的边心距OM= .
正六边形ABCDEF的面积是 面积的 倍,
2题图
1题图
轻轻告诉你:
与三角形各边都相切的圆叫做三角形的内切圆(圆心叫做三角形的内心)
各边都与圆相切的三角形叫做圆的外切三角形
2题图
3题图
1题图
归纳总结:
(1)一个三角形有 个内切圆.
(2)一个圆有 个外切三角形.
(3)三角形的内心就是三角形 的交点.
(4)三角形的内心到三角形 的距离相等.
8题图
7题图
4题图
2题图
归纳总结:
(1)圆的周长公式 .
(2)弧长 的计算公式是 .(记住)
……
_
图
7
-
2
_
图
7
-
1
图8
图9
A
B
O
图12-1
A
B
O
图12-2
图11
图10
3题图
归纳总结:
(1)圆的面积公式为:
(2)即扇形的面积公式为: 或 .(记住)
C
B
A
O
F
D
E
第9题图
A
B
C
2题图
4题图
C
A
B
3题图
1题图
6题图
5题图
归纳总结:
1.圆锥的侧面展开图一个扇形,扇形的半径就是圆锥母线长 .扇形的弧长就是圆锥底面圆的周长 .
2.设圆锥的母线长为 ,底面圆的半径为r,则它的侧面积为 .
(记住会用)
20cm
30cm
图2
A
图3
图1
图2
图1
A
B
D
C
A
B
D(B)
(A)
(D)
C
A
D
B
C
l
A
C
O
B
10题图
O
B
A
·
图10—2
图10—1
A
B
2米
4 米
(4)图
A
P
O
第8题图
第9题图
第11题图
第12题图
第5题图
第6题图
第9题图
A
M
O
B
P
M
A
N
E
D
O
图(1)
.
M
A
N
E
D
B
C
O
图(2)
班级: 姓名: 学号:
一、学习任务一
1.探究经过不同的点作圆。
(1)作经过已知点A的圆,这样的圆你能作出多少个?
(2)做经过已知点A,B的圆,这样的圆有多少个?它们的圆心分布有什么特点?
(3)作经过A,B,C,三点的圆,这样的圆有多少个?如何确定它的圆心?
由以上作圆可知过几个点作圆实质是确定圆心和半径,因此过一点的圆有___个,圆心是______,半径是_________.
过两点的圆有____个,圆心是______,半径是_____。过不在同一条直线上的三点_____________.圆心是__半径是__.
2.探究三角形的外接圆:
过三角形ABC三顶点作一个圆。
____________________________________三角形的外接圆.
_____________________________________________外心.
学习任务二:反证法
1.经过同一条直线的三个点能作出一个圆吗?你如何证明你的结论。
2.用反证法证明几何命题的一般步骤是:
二、合作共建(教师寄语:合作的基础是有自己的想法和辨别!)
1.如图是一块破碎的圆形木盖,试确定它的圆心.
2. 在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC的外接圆半径.
3.用反证法证明:一个三角形至少有两个角是锐角。
三、诊断评价(教师寄语:通过练习找出自己的不足! )
1.锐角三角形的外心在 ;直角三角形的外心在 ;钝角三角形的外心在 .
2.若AB=4cm,则过点A、B且半径为3cm的圆有 个.
3.直角三角形三个顶点都在以 为圆心,以 为半径的圆上,直角三角形的外心是 .
4.若Rt△ABC的斜边是AB,它的外接圆面积是121πcm2,则AB= .
5.已知a、b、c是△ABC三边长,外接圆的圆心在△ABC一条边上的是( )
A.a=15,b=12,c=1 B.a=5,b=12,c=12
C.a=5,b=12,c=13 D.a=5,b=12,c=14
6.一个三角形的外心在其内部,则这个三角形是( )
A.任意三角形B.直角三角形C.锐角三角形D.钝角三角形
7.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,则它的外心与顶点C的距离为( )
A.5cm B.6cm C.7cm D.8cm
8.下列说法错误的是( )
A.过直线上两点和直线外一点,可以确定一个圆
B.任意一个圆都有无数个内接三角形
C.任意一个三角形都有无数个外接圆
D.同一圆的内接三角形的外心都在同一个点上
9.已知Rt△ABC的两直角边为a和b,且a,b是方程x2-3x+1=0的两根,求Rt△ABC的外接圆面积.
10.求边长是6cm的等边三角形的外接圆的半径.
24.2.2直线和圆的位置关系(1)
班级: 姓名: 学号:
【课前预习】
点与圆的位置关系 数量关系
1:知识准备
【课堂活动】
2:探究1:(1)你看过日出吗?你知道太阳升起过程中,太阳和地平线会有几种不同位置关系吗?
(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点的个数吗?
发现:直线与圆有如下三种位置关系:
归纳:直线和圆有两个公共点,直线和圆 ,这条直线叫做圆的 .
直线和圆有一个公共点,直线和圆 ( http: / / www.21cnjy.com ) ,这条直线叫做圆的 ,这个点叫做 .直线和圆没有公共点,这条直线和圆 .
探究2: 设⊙O的半径为r,圆心到直线L的 ( http: / / www.21cnjy.com )距离为d,在直线和圆的不同位置关系中,d和r具有怎样的大小关系?反过来,你能根据d和r的大小关系来确定直线和圆的位置关系吗?
(a) (b) (c)
直线L和⊙O相交 d r,如图(a)所示;
直线L和⊙O相切 d r,如图(b)所示;
直线L和⊙O相离 d r,如图(c)所示.
例1.圆的直径是13,如果直线与圆心的距离分别如下,判断直线与圆的位置关系?并说明公共点的个数.⑴ 4.5 ⑵ 6.5 ⑶ 8
例2.在 Rt△ABC 中,∠C = 90 ( http: / / www.21cnjy.com )°,AC = 3 cm , BC = 4 cm ,以 C 为圆心,下列r 为半径的圆与AB有怎样的位置关系?⑴r=2cm ⑵r=2.4cm ⑶r=3cm
活动4:课堂小结
1、直线和圆的位置关系表:
直线和圆的位置关系 相交 相切 相离
公共点的个数
公共点名称
直线名称
圆心到直线的距离d与r的关系
2、确定直线与圆的位置关系的方法有____种
(1)根据定义,由___________ _______的个数来判断;
(2)根据性质,由_________________________ 的关系来判断。
24.2.2直线和圆的位置关系(学案纸1)
班级: 姓名: 学号:
随堂训练
1.⊙O的半径是5,点O到直线l的距离为4,则直线l与⊙O的位置关系为( )
A.相离 B.相切 C.相交 D.相交或相切
2.如果⊙O的直径为6厘米 ( http: / / www.21cnjy.com ),圆心O到直线AB的距离为5厘米,则直线与AB的位置关系为( )A.相离 B.相切 C.相交 D.不确定
3、已知⊙O的直径为10.(1)、若直线与⊙O相交,则圆心O到直线的距离d ________;
(2)、若直线与⊙O相切,则圆心O到直线的距离d ________;
(3)、若直线与⊙O相离,则圆心O到直线的距离d ________.
4、已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
5、已知△ABC 中,AB=AC=5,BC=6,以点A为圆心,以4为半径作⊙A ,⊙A 与直线BC的位置关系怎样。
【课后巩固】
一、判断
1、直线与圆最多有两个公共点。 ( )
2、若C为⊙O上的一点,则过点C的直线与⊙O相切。( )
3、若A、B是⊙O外两点, 则直线AB与⊙O相离。 ( )
4、若C为⊙O内一点,则过点C的直线与⊙O相交。 ( )
二、填空
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
3、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 _ 。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 _。
5、⊙O半径为r,圆心O到直线l的距离为d,且d与r是方程x2-9x+20 =
0的两根,则直线l与⊙O的位置关系是 。
6、如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
1)当直线AB与⊙M相离时, r的取值范围是______________;
2)当直线AB与⊙M相切时, r的取值范围是______________;
3)当直线AB与⊙M有公共点时, r的取值范围是___________.
三、选择题
1.⊙O的半径为4,圆心O到直线l的距 ( http: / / www.21cnjy.com )离为3,则直线l与⊙O的位置关系是( ) A.相交 B.相切 C.相离 D.无法确定
2、设⊙O的半径为4,点O到直线a ( http: / / www.21cnjy.com )的距离为d,若⊙O与直线a至多只有一个公共点,则d为…( )A、d≤4 B、d<4 C、d≥4 D、d=4
3、设⊙p的半径为4cm,直线l上 ( http: / / www.21cnjy.com )一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、相切或相交
四、解答题
如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?为什么?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆与直线AB分别有怎样的位置关系?
24.2.3切线的性质
班级: 姓名: 学号:
学习目标:1.记住切线的性质. 2.能利用切线的性质进行计算和证明
一.忆一忆 : 的直线是圆的切线 .
判断:1. 经过半径外端的直线是圆的切线 ( )
2. 垂直于半径的直线是圆的切线 ( )
3. 经过直径的外端且垂直于这条直径的直线是圆的切线( )
二.探究新知:
如图BC是⊙O的切线,切点为A,则BC经过切点 且BC与OA的位置关系为 。
三. 基础训练
1.如图所示,PA为⊙O的切线,切点为A, PA=, 则⊙O的半径为
2.如图AB与⊙O相切于点B,AO的延长线交⊙O于点C, 连接BC,若,则
3.如图AB与⊙O相切于点A,BO交⊙O于点C, ,则
4.已知直线CD与⊙O相切于C,AB为直径,若,则大小为
5.如图PT切⊙O于点T,若PT=4,PA=2, 则⊙O的半径为
6. 如图中,AB=AC,∠BAC=120°,BC与⊙A相切于点D与BA相交于E,则∠BDE=
7如图PA,PB分别切⊙O于A,B 则
四.提高训练
1.如图,AB为⊙O的直径,C为⊙O上的一点,AD与过C点的切线互相垂直于D, 求证:AC平分
2。如图⊙O的直径AB=6㎝,D为⊙O上的一点,且,过D的切线交AB延长线于C .求:①的度数 ②AC的长.
当堂检测A 姓名 当堂检测B 姓名
如图,已知⊙O中,AB是直径,过B点作⊙O 如图,已知⊙O中,AB是直径,过D点作⊙O
的切线BC,连结CO.若AD∥OC交⊙O于D. 的切线DC,连结CO.若AD∥OC交⊙O于D.
求证:CD是⊙O的切线. 求证:BC是⊙O的切线.
24.2.4垂径定理、切线的性质及判定
班级: 姓名: 学号:
学习目标:会用综合运用垂径定理、切线的性质及判定进行计算和证明.
一、忆一忆:
1.垂直于弦的直径的性质(垂径定理):
垂直于弦的直径 ,并且平分
已知:如图,CD是直径,与弦AB交于点M.
∵CD⊥AB ∴ AM=BM ( 根据: )
∵AM=BM ∴CD⊥AB ( 根据: )
2. 切线的判定定理:
经过 并且 的直线是圆的切线.(记住)
所以,直线是圆的切线必须满足(1) ;
(2) .
几何语言:直线经过⊙O的半径OA的外端点A , 且.
∴直线是⊙O的 .(根据 )
3. 切线的性质定理:圆的切线
几何语言为:∵ AB为⊙O的切线,切点为C
∴ AB⊥OC ( )
二、基础应用:
1.(04河北)如图1,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,OA=3,则cos∠APO的值为 .
2.(06河北)如图2,PA是⊙O的切线,切点为A,PA=,∠APO=30°,则⊙O的半径长为 .
3.(07河北)图3中,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,
BC⊥AD于点C,AB=2,半圆O的半径为2,则BC的长为 .
4.(08河北)如图4,与相切于点,的延长线交于点,连结.若
,则.
5如图,在直径AB=12的⊙O中,弦CD⊥AB于M,
且M是半径OB的中点,则弦CD的长 (保留根号)
6.如图,AB为⊙O的弦,⊙O的半径为5,OC⊥AB于点D,
交⊙O于点C,且CD=l,则弦AB的长是 .
7.如图,AB为⊙O的弦,⊙O的直径为10,OC⊥AB于点D,
交⊙O于点C,且AB=8,则CD的长是 .
三、能力提升:
1.(04河北中考)如图1,一个圆球放置在V形架中.图2是它的平面示意图,CA和CB都是⊙O的切线,切点分别是A,B.如果⊙O的半径为cm,且AB=6cm,求∠ACB.
2.(05河北)工人师傅为了检测该厂生产的一 ( http: / / www.21cnjy.com )种铁球的大小是否符合要求,设计了一个如图1所示的工件槽,其中工件槽的两个底角均为90°,尺寸如图(单位:cm)
将形状规则的铁球放入槽内时,若同时具有图1所示的A,B,E三个接触点,该球的大小就符合要求。
图2是过球心O及A,B,E ( http: / / www.21cnjy.com )三个接触点的截面示意图。已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD,BD⊥CD。请你结合图1中的数据。计算这种铁球的直径。
24.2.5切线长定理
班级: 姓名: 学号:
学习目标:1.知道什么是切线长.2.记住并会用切线长定理
一、学一学:
1.如图1,若AC为⊙O的切线,切点为C,则 ⊥ .
( 根据 )
若∠A=30°,半径为3cm,则线段AC= .
2.切线长:经过圆外一点做圆的切线,这点和切点之间的线段长
叫做这点到圆的切线长. 则图1中的切线长为 cm.
3.探究:如图2所示,PA、PB分别为⊙O的两条切线,切点分别为A、B.
(1)请你通过测量PA、PB的长度,猜想PA与PB满足的数量关系是PA PB;
(2)测量与的度数,猜想与大小关系是 .
并证明你的上述两猜想.
应用:
二、巩固应用:
类型一 利用切线长定理进行计算:
如图,PA、PB分别切⊙O于点A、B,劣弧AB的度数为1200(即所对
的圆心角度数)则∠APB= ,∠APO= ,∠ACB= ;
又知PA=6,则PB= ,圆的半径为 ,弦AB的长度为 .
2.如图,PA、PB、CD分别切⊙O于点A、B、E,请你找出图中
的等线段 、 、 .
若PA=6则△PDC的周长为 .
若∠P=600,⊙O的半径为2,则∠COD= ,△PDC的周长为 .
若点E为劣弧AB上一动点,过点E的⊙O的切线始终与AP,BP交
于点C、D,则△PDC的周长有无变化?为什么?
3. 如图,过半径为6c ( http: / / www.21cnjy.com )m的⊙O外一点P引圆的切线PA、PB,连结PO交⊙O于点F,过F作⊙O的切线分别交PA、PB于D、E,若PO=10cm,∠APB=40°.
(1)求△PED的周长 (2)求∠DOE的度数
类型二 利用切线长定理进行证明:
4.已知:如图,中,,O是AB上一点,以O为圆心,OB为半径的圆与AB交与点E,与AC相切于点D,求证:∥OC
检测A卷 姓名 检测B卷 姓名
1.如图:AE、AD、BC分别切⊙O于E、D、F. 1.如图:AE、AD、BC分别切⊙O于E、D、F
若,则的周长为 . 若,则的周长为 .
2.如图:⊙O 是ABC的内切圆,若∠ ( http: / / www.21cnjy.com )DEF=54° 2.如图:⊙O 是ABC的内切圆,若∠DEF=55°则BAC= ° 则BAC= °
24.2.6圆和圆的位置关系
班级: 姓名: 学号:
一、探索发现
1.观察与思考
下图是两个半径不同的⊙O1和⊙O2,从 ( http: / / www.21cnjy.com )左向右移动⊙O1,你能发现在移动过程中,⊙O1和⊙O2有这5种不同的位置,请你填出每种位置关系时,两圆的交点个数.
交点个数:
2.学一学
(1)如果两个圆没有公共点,那么就说这两 ( http: / / www.21cnjy.com )个圆相离,如图 和 ,相离又分为外离(即一个圆在另一个圆的外部)和内含(即一个圆在另一个圆的内部). 则上图中表示外离的是图 ,表示内含的是图 .
(2)如果两个圆只有一个公共点,那么就说这两个圆相切,如图 和 ,
相切又分为内切和外切.则上图中表示内切的是图 ,表示外切的是图 .
(3)如果两个圆有两个公共点,那么就说这两个圆 .
3.探究 用数量关系识别两圆的位置关系.
设两圆的半径分别为R、r(R>r),圆心距(两圆圆心的距离)为.
二、拓展应用:
类型一:判断两圆的位置关系
1.已知平面内两圆的半径分别为4和6,圆心距是2,则两圆的位置关系是 .
2.已知⊙O1和⊙O2的半径分别为2cm和5cm,且O1O2=6 cm,则⊙O1和⊙O2的位置关系是 .
3. 已知⊙O1和⊙O2的半径分别为3cm和7cm,且O1O2=10cm,则⊙O1和⊙O2的位置关系是 .
4.两圆的半径分别是4cm和3cm,圆心距为1cm,则两圆的位置关系是 ;
5.已知⊙O1和⊙O2的半径分别为R、r, O1O2=5cm,,R=3,当0
1. 有两个圆,一个圆的半径R=4,两圆的圆心距是5,另一个圆的半径r满足条件 时,这两个圆外离.
2.两圆的圆心距为2cm,一个圆的半径为10cm,要使这两个圆内含,另一个圆的半径r应满足条件
3. 半径为1和5的两圆相交,则圆心距d的取值范围为 ;
4. 已知两圆的直径分别为4和6,且这两个圆有唯一公共点,则圆心距d为
5. 已知两圆半径之比为1:2,当两圆相切时,圆心距为8 ,则大圆半径为 ;
6. ⊙O的半径为2,点P是⊙O外一点,OP的长为3,则以点P为圆心,且与⊙O相切的圆的半径为 .
7. 已知两圆内切,圆心距为2cm,如果一个圆的半径是3cm,则另一个圆的半径为 .
8. 相切两圆的圆心距为5,其中一个圆的半径为3,则另一个圆的半径为 .
9. 已知⊙O的半径为5cm,点P是⊙O外一点,OP=8cm,以P为圆心作⊙P与⊙O相切,求⊙P的半径.(写出过程,要考虑全面)
检测A卷 姓名 检测B卷 姓名
1.已知⊙O1和⊙O2的半径分别为3 ( http: / / www.21cnjy.com )cm和7cm, 1.已知⊙O1和⊙O2的半径分别为4cm和6cm,且O1O2=6 cm,则⊙O1和⊙O2的位置关系是 . 且O1O2=6 cm,则⊙O1和⊙O2的位置关系是 .
2.已知两圆的直径分别为6和8,且这两个圆 2.已知两圆的直径分别为10和4,且这两个圆
有唯一公共点,则圆心距d为 有唯一公共点,则圆心距d为
24.3.1正多边形和圆
学习目标:1.知道正多边形的相关概念 2.会解决正多边形问题.
一.忆一忆:
正三角形 正方形 正五边形 正六边形 … 正n边形
内角和 …
每一个内角 …
二.学一学:
2.如图:有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积.
三.练一练:根据表中提供的数值,把其它数据补充完整(正六边形可用上图分析).
四、拓展应用:
1.如图:要拧开一个边长a=12cm的六角形螺帽,扳手张开口b至少要多少?
2.如图,梯形ABCD的四条边都与⊙O相切,切点分别为E、F、G、H.
(1)请你探索AD+BC与AB+CD之间的数量关系.
(2)请你探索DO与CO的位置关系.
(3)若梯形ABCD不是梯形,结论(1)和(2)是否成立,
若成立请给出证明,不成立说明理由.
检测A卷 姓名 检测B卷 姓名
1.边长为的正六边形的一边所对的圆周角 1.边长为的正六边形的一边所对的圆周角
等于 °;面积为 等于 °;面积为
2.如图,点M、N分别是正八边形一组临边 2.如图,点M、N分别是正十边形一组临边
AB、BC上的点,且AM=BN,点O是正八边形 AB、BC上的点,且AM=BN,点O是正十边形
的中心,则∠MON= °. 的中心,则∠MON= °.
24.3.2三角形内切圆
班级: 姓名: 学号:
学习目标:1.知道什么是三角形的内切圆.
2.会解决与三角形的内切圆有关的问题.
一、忆一忆:
1.画出同时经过点A、B、C的⊙O.
2.经过三角形的三个顶点可以作 ( http: / / www.21cnjy.com )圆,这个圆叫做三角形的 ,三角形叫作圆的 ,外接圆的圆心是三角形 的交点,叫做这个三角形的 心.
三角形的外心到三角形 相等.
eq \o\ac(○,3)锐角三角形的外心在三角形的 ( http: / / www.21cnjy.com ) ,直角三角形的外心在三角形的 ,钝角三角形的外心在三角形的 .
任何三角形都有 个外接圆,圆有 个内接三角形.
二、学一学:
1.已知,如图1,⊙O与△ABC的三边分别相切于点D、E、F.
圆心O到三角形三边的距离 ,因为:
圆心O是三角形的 的交点,根据
2.画出下列锐角三角形、直角三角形和钝角三角形的内切圆.
3. 画出⊙O的外切三角形,看能画几个?
三、巩固应用:
1. 如图,O是△ABC的内心.(1) ( http: / / www.21cnjy.com )若∠ABC=500,∠ACB=700,则∠O= ,(2)若∠A=800,则∠O= ,(3)若∠O=1300,则∠A= .
2. 如图,△ABC内接于⊙O,I是△ABC的内心,∠BIC=1300,则∠A ,∠BOC= .∠OBC= .
3. 直角三角形两直角边长分别为5和12,求其内切圆的半径和外接圆的半径为.
4.如图,⊙O切△ABC的三边于点E、F、 G,若AB=9,BC=10,AC=6,求AG、GC、BF的长.
四、知识超市:
5.Rt△ABC中,∠ACB=900,AC=9,BC=24,⊙O为其内切圆,则∠AOB= ,
⊙O的半径为 ,其外接圆的半径为 .
6.正三角形内切圆半径为1,那么这个三角形的边长为
7.如图,点I是△ABC的内心,∠A=800,则∠BIC的度数为 .
8.如图,⊙O是△ABC的内切圆,H为⊙O上任意点,MN切⊙O于H,交AB、AC于点M、N,已
知△ABC的周长为20cm,BC=6cm.则△AMN的周长为
五、能力提升:
在Rt△ABC中,斜边AB=10cm,其内切圆半径为2cm,
则△ABC的面积为 .
检测A卷 姓名 检测B卷 姓名
1. 如图,点O是△ABC的内心,∠BOC =120°, 1. 如图,点O是△ABC的内心,∠BOC =130°,
则∠A的度数为 . 则∠A的度数为 .
2.已知三角形三边长分别为3 , 4 , 5,则它的 2.已知三角形三边长分别为6 , 8 , 10,则它的 内切圆半径为 内切圆半径为
外接圆半径为 外接圆半径为
24.4.1弧长公式扇形面积
班级: 姓名: 学号:
学习目标:记住并会用弧长公式.
一、探究:弧长公式
如右图,在半径为R的圆中,圆的周长.因为的圆心角所对的弧长就是圆的周长,所以的圆心角所对的扇形MON弧长 . 的圆心角所对的扇形AOB弧长.即弧长的计算公式是 .
二、利用弧长公式求弧长、圆心角度数、及圆的半径.
1.一条弧所对的圆心角为90°,半径为3,则这条弧长为 。
2.若一条弧长为72,圆心角为36°,则半径为 。
3.若一条弧长为240,半径为180,则圆心角为 。
4.在半径为3的⊙O中,弦AB=3,则的长为 。
5.如图,∠AOB=90°∠B=20°,以点O为圆心,OA长为半径的圆交AB于点C,若AO=12则的长为 .
6.时钟的轴心到分针针端的长为,那么经过40分钟,分针针端转过的弧长是 .
三、能力提升.
7.如图1…3是边长大于2的 ( http: / / www.21cnjy.com )三角形、四边形、…、凸n边形.分别以它们的个顶点为圆心,以1为半径画弧与相邻边相交,得到3条弧、4条弧、…、n条弧.
(1)图1中的3条弧的弧长的和为 ,图2中的4条弧的弧长的和为
(3)图3中n条弧的弧长的和为 (用含n的式子表示).
检测A卷 姓名 检测B卷 姓名
1.一条弧所对的圆心角为80°,半径为6, 1.一条弧所对的圆心角为60°,半径为6,
则这条弧长为 。 则这条弧长为 。
2.若一条弧长为12,圆心角为120°, 若一条弧长为14,圆心角为120°,
则半径为 。 则半径为 。
24.4.1弧长专练
班级: 姓名: 学号:
学习目标:记住并会用弧长公式.
1.(05咸阳)如图2所示,一条公路的转弯处是一段圆弧(圆中的弧AB),点O是这段弧的圆心,AB﹦120m,OA﹦120m则这段弯路AB长为 m(保留).
2.(07兰州)如图3-1所示,小丽自 ( http: / / www.21cnjy.com )己动手做了一顶圆锥形的圣诞帽,母线长30cm,底面半径10cm,她想在帽子上缠一根漂亮的丝带,从点A出发绕帽子侧面一周,至少需丝带
3.(05内江)如图4-1,有一圆锥形 ( http: / / www.21cnjy.com )粮堆,其主视图是边长为6m的正三角形ABC,母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是 m(结果不取近似数).
4.(06株州)我国南方一些地区的农民戴 ( http: / / www.21cnjy.com )的斗笠是圆锥形.已知圆锥的母线长为30 cm,底面圆的半径为24 cm,则圆锥侧面积为 cm2.
5.(05河南)图7-1、7-2是用两种方法 ( http: / / www.21cnjy.com )把6根圆形钢管用钢丝绳捆扎的截面图.设7-1、7-2两种方法捆扎所需钢丝绳的长度分别为a、b(不计接头部分)则a、b的大小关系为a b.
6.06山西)图8是某圆柱形网球筒,其底面直径是10cm,长
为80cm,将七个这样的网球筒如图所示放置并包装侧面,则需
________________的包装膜(不计接缝,π取3)。
7.(2010 嵊州市)如图9,是7根圆柱形木棒的横截面圆的半径均
为1,则捆扎这7根木棒一周的绳子长度为 。
8.(06河南)如图10,一块含有30°角的直角三角板ABC,
在水平桌面上绕点C按顺时针方向旋转到的位置,若
BC的长为15 cm,那么顶点A从开始到结束所经过的路径长为____________
9.(06济南)如图11,矩形ABC ( http: / / www.21cnjy.com )D中,AB=8,AD=6,将矩形ABCD在直线上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
10.(07台湾)如图(12-1),水平地面上有一面积为30 平方公分的灰色扇形OAB,其中的长度为6公分,且与地面垂直。若在没有滑动的情况下,将图(12-1)的扇形向右滚动至垂直地面为止,如图(12-2)所示,则O点移动 公分.
24.4.2扇形面积
学习目标:记住并会用扇形面积.
一、探究:扇形面积
如图,在半径为R圆中,因为的圆心角所对的扇形面积就是圆的
面积 , 所以的圆心角所对的扇形面积
所以圆心角是扇形面积.
二、利用扇形面积计算公式进行计算
1.一扇形半径为60cm, 圆心角为150°,则扇形的面积是 .
2.一扇形的弧长为20 cm ,面积为 240cm2 ,,则扇形的圆心角是 .
3.如图所示,一扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°AB=30cm
贴纸部分BD长为20cm,则贴纸部分的面积为 .
4.(08南昌)如图,为的直径,于点,交于点,于点.(1)请写出三条与有关的正确结论;
(2)当,时,求圆中阴影部分的面积.
能力提升:
1.如图,⊙A,⊙B,⊙C两两不相交,且半径都是0.5cm,
则图中的三个扇形(即阴影部分)的面积 .
2.如图A是半径为2的⊙O外一点,OA=4,
AB是⊙O的切线,点B是切点,BC∥OA,
连接AC,则阴影部分的面积等于
扇形面积专练
学习目标:记住并会用扇形面积.
1.(05年·江苏)如图所示,Rt△A ( http: / / www.21cnjy.com )BC的面积为20cm2,在AB的同侧,分别以AB、BC、AC为直径作三个半圆,阴影部分的面积 .
2.(2010云南昆明)如图,在△ABC ( http: / / www.21cnjy.com )中,AB = AC,AB = 8,BC = 12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是
3.(2010湖南衡阳)如图,在R ( http: / / www.21cnjy.com )t△ABC中,∠C=90°,AC=4,BC=2分别以AC、BC为直径画半圆,则图中阴影部分的面积为 .(结果保留π)
4.(2010山东临沂) 如图,直径为6的半径,绕点逆时针旋转60°,此时点到了点,则图中阴影部分的面积是
5.如图,△ABC是正三角形,曲线CDEF…叫做“正三角形的渐开线”,其中弧、、、的圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则
曲线CD的长;曲线DE的长;曲线EF的长为第n段曲线的长;则
;则
6.(2010湖北黄石)如图,从一个 ( http: / / www.21cnjy.com )直径为2的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为
24.4.3圆锥的侧面展开图
学习目标:会计算圆锥的侧面积和全面积.
一、学一学:
1.圆锥的母线:我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.如图中.
2.圆锥的高:连接顶点和底面圆心的线段叫做圆锥的高. 如图中h就是圆锥的高.
二、探究与思考:
如图,圆锥是由一个底面和一个侧面围成的,沿圆锥的一条母线将圆锥侧面剪开并展平,可以得到圆锥的侧面展开图是一个扇形,设圆锥的母线长为,底面圆的半径为r,那么侧面展开图扇形的半径为圆锥的母线长,扇形的弧长(即底面圆的周长)为 ,由扇形的面积公式可得圆锥侧面展开图的面积为= ,圆锥的底面积为 ,圆锥的全面积为 .(圆锥的全面积=侧面积+底面积).
三、巩固应用:
1.已知圆锥的底面半径为80cm,母线长90cm,则它的侧面积为 ,全面积为
侧面展开图圆心角的度数为 .
2.已知圆锥的底面半径为3,高为4,则这个圆锥的母线长为 ,侧面积为 .
3.圆柱的高为20cm,底面半径是高的,那么圆柱的侧面积为 。
4. 若圆锥的母线长为6cm,侧面展开图的圆心角为的扇形,则圆锥底面半径为 cm.
5.若用半径为15cm,圆心角为的扇形围成一个圆锥的侧面,这个圆锥的高为 cm.
6.圆锥的侧面积为,母线长为3,侧面展开图(扇形)的圆心角为
四、中考真题回放
1.(2003,河北)已知圆锥的底面直径为4,母线长为6,则它的侧面积为 。
2.(2004河北)如图1,在正方形铁 ( http: / / www.21cnjy.com )皮上剪下一个圆形和扇形,使之恰好围成图3—2所示的一个圆锥模型.设圆的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为( )
A.R=2r B.R=r
C.R=3r D.R=4r
3.(04河北)图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽的纸的面积为 cm2
(π取3.14).
4. (05河北)如图3,已 ( http: / / www.21cnjy.com )知圆锥的母线长OA=8,底面圆的半径为r=2,若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线长为
(结果保留跟号)
5.(09,唐山模拟)如图 ( http: / / www.21cnjy.com )1,O为圆柱形木块底面的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24cm,AB=25cm.测量出AD所对的圆心角为120°,如图2所示.
(1)求⊙O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留 和根号)
《弧长、扇形等面积》
学习目标:会计算弧长和扇形面积
1.已知扇形的圆心角为,半径为2cm,则扇形的弧长是 cm,扇形的面积是____ .
2. (2006 梅州课改)如图,两个半圆中,小圆的圆心在大的直径上,长为4的弦与直径平行且与小半圆相切,那么圆中阴影部分面积等于 .
3.如图,一块含有角的直角三角板,在水平桌面上绕点按顺时针方向旋转到的位置.若的长为,那么顶点从开始到结束所经过的路径长为 .
4.如图,的边长都大于2,分别以它的顶点为圆心,1为半径画弧(弧的端点分别在三角形的相邻两边上),则这三条弧的长的和是 .
5.如图,,,,相互外离,它们的半径都是,顺次连结四个圆心得到四边形,则图中四个扇形(阴影部分)的面积之和等于__________.(结果保留)
6.如图,,为的中点,都是半径为3的的切线,为切点,则的长为 .
7.将边长为8cm的正方形的四边沿直线向右滚动(不滑动),当正方形滚动两周时,正方形的顶点所经过的路线的长是 cm.
8.如图,的半径为3,,切于,弦,连结,图中阴影部分的面积为 .
9.如图,有一圆锥形粮堆,其正视图是边长为 ( http: / / www.21cnjy.com )6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是______m(结果不取近似值).
10.(2005年成都市)农村常搭建橫截面为 ( http: / / www.21cnjy.com )半圆形的全封闭塑料薄膜蔬菜大棚,如图所示,如果不考虑塑料薄膜接头重合及埋在土里的部分,那么搭建一个这样的蔬菜大棚需用塑料薄膜的面积是 .
11.图10—1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图10—2是车棚顶部截面的示意图,所在圆的圆心为O.
车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留).
圆(单元论坛)
圆的有关性质
1.圆是 轴对称图形, 的直线都是它的对称轴,有 条对称轴,圆
是中心对称图形,又是旋转对称图形,即旋转任意角度都和自身重合. 对称中心.
2.外心—是三角形 的圆心 到三角形 的距离相等.
(是 的交点)
内心—是三角形 的圆心 到三角形 的距离相等.
3. 垂径定理及推论:
如图:AB是⊙O的直径,CD是弦。
(1)若AB⊥CD 则有 PC=PD且 =
根据:
(2)若PC=PD 则有 AB⊥CD 且 =
根据:
垂径定理
1、已知OC⊥AB 2、已知弦AB= 3、已知⊙O半径2 4、已知直径AB⊥CD,
OC=3,AB=8 ∠AOB=120° 弦AB= BE=1,弦CD=10
则⊙O半径 则⊙O半径 则∠AOB= 则⊙O半径
圆心角、弧、弦之间的关系:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等它们所对应的其余各组量分别 .
如图,若∠AOB=∠BOC则有 , .
圆心角和圆周角的关系:
的角叫圆心角;
角叫圆周角.
(2)一条弧所对的圆周角等于它所的圆心角的 ,在同圆或等圆中,同弧或等弧所对的圆周角 ,直径所对的圆周角是 ,的圆周角所对的弦是 .
①若则 . ②若则
③若 AB是⊙O的直径,则∠ACB= ④若∠ACB是直角,则弦AB是
点和圆的位置关系:
设圆的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在圆外d r; (2) 点P在圆上d r; (3)点P在圆内d r;
6.直线和圆的位置关系:
设⊙O的半径为r,圆心O到直线的的距离为d,则有:
直线与⊙O相离 ; 直线与⊙O相切 ;直线与⊙O相交 .
7.圆和圆的位置关系:
设两圆的半径分别为R、r(R>r),圆心距(两圆圆心的距离)为
(1)两圆外离;(2)两圆外切 ;(3)两圆相交 <<
(4)两圆内切 ;(5)两圆内含 .(记住上述数量关系)
练一练:
①已知平面内两圆的半径分别为4和6,圆心距是2,则两圆的位置关系是 .
②已知⊙和⊙的半径分别为2cm和5cm,且,则⊙和⊙的位置关系是 .若两圆相切,则圆心距为 .
③已知⊙和⊙的半径分别为3cm和7cm,且,则⊙和⊙的位置关系是 .
④两圆的半径分别是4cm和3cm,圆心距为1cm,则两圆的位置关系是 ;
⑤已知⊙和⊙的半径分别为R、r,R=3,当时,则⊙和⊙的位置关系是 .
8.切线的判定和性质:
切线的判定:
①到圆心的距离等于半径的直线是圆的 ;
②经过半径的外端并且 这条半径的直线是圆的切线.
(2)切线的性质:圆的切线 经过切点的半径.
①如图①所示,PA为⊙O的切线,切点为A, PA=, 则⊙O的半径为
②如图②AB与⊙O相切于点B,AO的延长线交⊙O于点C, 连接BC,若,则
③如图③AB与⊙O相切于点A,BO交⊙O于点C, ,则
④已知直线CD与⊙O相切于C,AB为直径,若,则大小为
9.圆的有关计算:
(1)弧长 .
①一条弧所对的圆心角为90°,半径为3,则这条弧长为 。
②若一条弧长为72,圆心角为36°,则半径为 。
③若一条弧长为240,半径为180,则圆心角为 。
(2)扇形面积:S= 或S=
①一扇形半径为60cm, 圆心角为150°,则扇形的面积是 .
②一扇形的弧长为20 cm ,面积为 240cm2 ,,则扇形的圆心角是 (3)圆锥:①圆锥的侧面展开图是一个 。圆锥的母线 扇形半径R.
圆锥的底面圆周长 扇形弧长.
②圆锥的侧面积等于设圆锥的母线长为,底面圆的半径为r,则它的侧面积为 . + .(记住会用)
跟踪训练:
①已知圆锥的底面半径为80cm,母线长90cm,则它的侧面积为 ,全面积为
侧面展开图圆心角的度数为 .
②已知圆锥的底面半径为6,高为8,则这个圆锥的母线长为 ,侧面积为 .
③圆柱的高为40cm,底面半径是高的,那么圆柱的侧面积为 。
④若圆锥的母线长为6cm,侧面展开图的圆心角为的扇形,则圆锥底面半径为 cm.
24.2.1点和圆的位置关系
【自主学习】
(一)复习巩固:
1.已知AB是⊙O的直径,C是⊙O上一点,若AB=4cm,AC=3cm,则BC= .
2.下列命题:①直径所对的角 ( http: / / www.21cnjy.com )是900 ;②直角所对的弦是直径;③相等的圆周角所对的弧相等;④对同一弦的两个圆周角相等.正确的有( )A. 0个 B. 1个 C.2个 D.3个
(二)新知导学
1.过不在同一直线上的三个点确定 圆.
2.经过三角形的三个顶点的圆叫做三角形的 ,外接圆的圆心叫做三角形的 ,
这个三角形叫圆的 三角形.
【合作探究】
要将如图所示的破圆轮残片复制完成,
怎样确定这个圆轮残片的圆心和半径
(写出找圆心和半径的步骤).
【自我检测】
一、填空题:
1.锐角三角形的外心在_______.如果一个三角形的外心在它的一边的中点上, 则该三角形是______.如果一个三角形的外心在它的外部,则该三角形是_____.
2.边长为6cm的等边三角形的外接圆半径是________.
3.△ABC的三边为2,3, ,设其外心为O,三条高的交点为H,则OH的长为_____.
4.三角形的外心是______的圆心,它是_______的交点,它到_______的距离相等.
5.已知⊙O的直径为2,则⊙O的内接正三角形的边长为_______.
6.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用________ 次就可以找到圆形工件的圆心.
二、选择题:
7.下列条件,可以画出圆的是( )
A.已知圆心 B.已知半径;
C.已知不在同一直线上的三点 D.已知直径
8.三角形的外心是( )
A.三条中线的交点; B.三条边的中垂线的交点;
C.三条高的交点; D.三条角平分线的交点
9.下列命题不正确的是( )
A.三点确定一个圆 B.三角形的外接圆有且只有一个
C.经过一点有无数个圆 D.经过两点有无数个圆
10.一个三角形的外心在它的内部,则这个三角形一定是( )
A.等腰三角形 B.直角三角形; C.锐角三角形 D.等边三角形
11.等腰直角三角形的外接圆半径等于( )
A.腰长 B.腰长的倍; C.底边的倍 D.腰上的高
12.平面上不共线的四点,可以确定圆的个数为( )
A.1个或3个 B.3个或4个 C.1个或3个或4个 D.1个或2个或3个或4个
三、解答题:
13.如图,A、B、C三点表示三个工厂,要 ( http: / / www.21cnjy.com )建立一个供水站, 使它到这三个工厂的距离相等,求作供水站的位置(不写作法,尺规作图,保留作图痕迹).
14.如图,已知△ABC的一个外角∠C ( http: / / www.21cnjy.com )AM=120°,AD是∠CAM的平分线,且AD与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.(1)判断△FBC的形状,并说明理由.
(2)请给出一个能反映AB、AC和FA的数量关系的一个等式,
并说明你给出的等式成立.
15.如图,在钝角△ABC中,AD ( http: / / www.21cnjy.com )⊥BC,垂足为D点,且AD与DC的长度为x2-7x+12=0的两个根(AD
24.2.2直线和圆的位置关系(1)
新知导学
1.直线与圆的位置关系
①定义:直线与圆有 个公共点时,叫做直线与圆相交,这条直线叫做圆的 线.
直线与圆有 个公共点时,叫做直线与圆相切,这条直线叫做圆的 线.这个公
共点叫做 点.直线与圆有 个公共点时,叫做直线与圆相离.
直线与圆的位置关系的性质与判定
设⊙O的半径为r,圆心O到直线的距离为d,那么
直线与圆相交 ;
直线与圆相切 ;
直线与圆相离 .
【合作探究】
1.在△ABC中,∠A=450,AC=4,以C为圆心,r为半径的圆与直线AB有交点,试确定r的范围.
【自我检测】
一、选择题
1.命题:“圆的切线垂直于经过切点的半径”的逆命题是( )
A.经过半径的外端点的直线是圆的切线.B.垂直于经过切点的半径的直线是圆的切线.
C.垂直于半径的直线是圆的切线. D.经过半径的外端并且垂直于这条半径的直线是圆的切线.
2.如图,AB、AC与⊙O相切于 ( http: / / www.21cnjy.com )B、C,∠A=500,点P是圆上异于B、C的一个动点,则∠BPC的度数是( )A.650 B.1150 C.650或1150 D.1300或500
3.已知正三角形的边长为6,则该三角形外接圆的半径为( )
A. B.3 C. D.1
4.如图,BC是⊙O直径,P是CB延长线上一点,PA切⊙O于A,如果PA=,OB=1,那么∠APC等于( )A. 150 B.300 C.450 D.600
5.如图,线段AB经过圆心O,交⊙O于 ( http: / / www.21cnjy.com )点A、C,∠B=300,直线BD与⊙O切于点D,则∠ADB的度数是( )A.1500 B.1350 C.1200 D.1000
6.在平面直角坐标系中,以点(2,1)为圆心,1为半径的圆,必与( )
A. x轴相交 B. y轴相交 C. x轴相切 D. y轴相切
7.如图,⊙的直径与弦的夹角为,切线与的延长线交于点,若⊙的半径为3,则的长为( )A.6 B. C. 3 D.
二、填空题
8.如图,已知直线CD与⊙O相切于点C,AB为直径,若∠BCD=40°,则∠ABC的大小等于_____.
9.如图,PA是⊙O的切线,切点为A,PA=,∠APO=30°,则⊙O的半径长为_______.
10.如图,图同第7题,AB是⊙O的直径,BD=OB,∠CAB=300.,写出三个正确结论
(除AO=OB=BD外):①___ ( http: / / www.21cnjy.com )_________________;②____________________;③____________________.
11.已知∠AOB=300,M为OB边上任意一点,以M为圆心,2cm为半径作⊙M. 当OM=_______cm时,⊙M与OA相切(如图).
12.如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过
点D作DE⊥AC,垂足为E. 根据以上条件写出三个正确的结论(除AB=AC,AO=BO, ABC=∠ABC外)是:
(1) ___________________;(2) ___________________;(3) __________________
三、解答题
13.如图,∠PAQ是直角,⊙O 与AP相切于点T,与AQ交于B、C两点.
(1)BT是否平分∠OBA?说明你的理由;
(2) 若已知AT=4,弦BC=6,试求⊙O 的半径R.
14.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC.
(1) 求证:△BAD∽△CED; (2) 求证:DE是⊙O的切线.
24.2.2直线和圆的位置关系(2)
新知导学
1.切线的判定定理:经过半径的 并且 这条半径的直线是圆的切线.
2.切线的性质定理:圆的切线 于经过切点的 .
3.与三角形各边都 的圆叫做三角形的 圆, 圆的
叫做三角形的 ,这个三角形叫做圆的 三角形.
【合作探究】
如图,AB、CD分别与半圆O切于点A、D,BC切⊙O于点E,若AB=4,CD=9,
求⊙O的半径.
2.已知锐角△ABC,作△ABC的内切圆.
【自我检测】
一、选择题
1.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论错误的是( )
A. ∠1=∠2 B.PA=PB C.AB⊥OP D.
2.如图,⊙O内切于△ABC,切点为D ( http: / / www.21cnjy.com )、E、F,若∠B=500,∠C=600,连结OE、OF、DE、DF,则∠EDF等于( )A.450 B.550 C.650 D.700
3.边长分别为3、4、5的三角形的内切圆与外接圆半径之比为( )
A.1:5 B.2:5 C.3:5 D.4:5
4.如图,PA、PB是⊙O的两条切线,切点是A、B. 如果OP=4,,那么∠AOB等于( )A. 90° B. 100° C. 110° D. 120°
5.如图,已知⊙O过边长为正2的方形ABCD的顶点A、B,且与CD边相切,则圆的半径为( )A. B. C. D.1
6.如图,⊙O为△ABC的内切圆,∠C=900,AO的延长线交BC于点D,AC=4,CD=1,
则⊙O的半径等于( )A. B. C. D.
1题图 2题图 4题图
二填空题
7. 直角三角形有两条边是2,则其内切圆的半径是__________.
8. 正三角形的内切圆半径等于外接圆半径的__________倍.
9.如图,PA、PB是⊙O的切线,点A、B为切点,AC是⊙O的直径,∠BAC=200,则∠P的大小是___度.
10.等边三角形ABC的内切圆面积为9π,则△ABC的周长为_________.
11.已知三角形的三边分别为3、4、5,则这个三角形的内切圆半径是 .
12.三角形的周长是12,面积是18,那么这个三角形的内切圆半径是 .
三、解答题:
13.已知如图,过圆O外 ( http: / / www.21cnjy.com )一点B作圆O的切线BM, M为切点.BO交圆O于点A,过点A作BO的垂线,交BM于点P.BO=3,圆O半径为1.求MP的长.
14.如图,AB是半圆O的直径,点 ( http: / / www.21cnjy.com )M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.(1) 当∠PQA=600时,请你对△QCP的形状做出猜想,并给予证明;
(2) 当QP⊥AB时,△QCP的形状是__________三角形;
(3) 由(1)、(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时, △QCP一定是_________三角形.
15.已知:∠MAN=30°,O为边AN上一点,以O为圆心、2为半径作⊙O ,交AN于D、E两点,设AD=.
⑴ 如图⑴当取何值时,⊙O与AM相切;
⑵ 如图⑵当为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
24.2.3 圆和圆的位置关系
(一)复习巩固:
1圆的切线的性质定理: .
2.圆的切线的判定定理: .
3.三角形的内心是它的 圆的圆心,它是三角形 的交点.
4.内心到三角形 的距离相等,到三角形三边距离相等的点是 .
5.已知三角形的面积为12,周长为24,则内切圆的半径为 .
(二)新知导学
圆与圆的五种位置关系的性质与判定
如果两圆的半径为R、r,圆心距为d,那么
两圆外离 ;两圆外切 ;
两圆相交 ;两圆内切 ;
两圆内含 .
(位置关系) (数量关系)
【合作探究】
1.已知两圆相切,一个圆的半径为5,圆心距d=2,求另一个圆的半径.
2.半径为1、2、3的三个圆两两外切,求这三个圆的圆心的连线构成的三角形的面积.
【自我检测】
一、填空题:
1.已知两圆半径分别为8、6,若两圆内切,则圆心距为______;若两圆外切,则圆心距为___.
2.已知两圆的圆心距d=8,两圆的半径长是方程x2-8x+1=0的两根,则这两圆的位置关系是______.
3.圆心都在y轴上的两圆 ( http: / / www.21cnjy.com )⊙O1、⊙O2,⊙O1的半径为5,⊙O2的半径为1,O1 的坐标为(0,-1),O2的坐标为(0,3),则两圆⊙O1与⊙O2的位置关系是________.
4.⊙O1和⊙O2交于A、B两点,且⊙O1经过点O2,若∠AO1B=90°,那么∠AO2B 的度数是__.
5.矩形ABCD中,AB=5,BC ( http: / / www.21cnjy.com )=12,如果分别以A、C为圆心的两圆相切,点D在⊙C内, 点B在⊙C外,那么圆A的半径r的取值范围是__________.
6.两圆半径长分别是R和r(R> ( http: / / www.21cnjy.com )r),圆心距为d,若关于x的方程x2-2rx+(R-d)2=0 有相等的两实数根,则两圆的位置关系是_________.
二、选择题
7.⊙O的半径为2,点P是⊙O外一 ( http: / / www.21cnjy.com )点,OP的长为3,那么以P为圆心,且与⊙O 相切的圆的半径一定是( ) A.1或5 B.1 C.5 D.1或4
8.直径为6和10的两上圆相外切,则其圆心距为( ) A.16 B.8 C.4 D.2
9.如图1,在以O为圆心的 ( http: / / www.21cnjy.com )两个圆中,大圆的半径为5,小圆的半径为3, 则与小圆相切的大圆的弦长为( ) A.4 B.6 C.8 D.10
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1) (2) (3)
10.⊙O1、⊙O2、⊙O3两两外切,且半径分别为2cm,3cm,10cm,则△O1O2O3 的形状是( )
A.锐角三角形 B.等腰直角三角形; C.钝角三角形 D.直角三角形
11.如图2,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线, 切点为A,则O1A的长为( ) A.2 B.4 C. D.
12.半径为1cm和2cm的两 ( http: / / www.21cnjy.com )个圆外切,那么与这两个圆都相切且半径为3cm 的圆的个数是( ) A.5个 B.4个 C.3个 D.2个
13.如图3,⊙O的半径为r,⊙O1、⊙O2 ( http: / / www.21cnjy.com )的半径均为r1,⊙O1与⊙O内切,沿⊙O 内侧滚动m圈后回到原来的位置,⊙O2与⊙O外切并沿⊙O外侧滚动n圈后回到原来的位置,则m、n的大小关系是( ) A. m>n B. m=n C. m
14.若两圆的圆心距d满足等式│d-4│=3,且两圆的半径是方程x2-7x+12=0 的两个根,试判断这两圆的位置关系.
15.某人用如下方法测一钢管的内径: ( http: / / www.21cnjy.com )将一小段钢管竖直放在平台上, 向内放入两个半径为5cm的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD的长.
16.如图,⊙O1、⊙O ( http: / / www.21cnjy.com )2交于A、B两点,点O1在⊙O2上,两圆的连心线交⊙O1于E、D,交⊙O2于F,交AB于C,请根据图中所给的已知条件(不再标注其他字母, 不再添加任何辅助线),写出两个线段之间的关系式.
24.3正多边形和圆
(一)复习巩固
1. 等边三角形的边、角各有什么性质? .
2. 正方形的边、角各有什么性质? .
(二)新知导学
1.各边 ,各角 的多边形是正多边形.
2.正多边形的外接圆(或内切圆)的圆心叫做 ,外接圆的半径叫做 ,
内切圆的半径做 .正多边形各边所对的外接圆的圆心角都 .正多边形每一边所对的外接圆的圆心角叫做 .正n边形的每个中心角都等于 .
3.正多边形都是 对称 ( http: / / www.21cnjy.com )图形,正n边形有 条对称轴;正 数边形是中心对称图形,对称中心就是正多边形的 ,正 数边形既是中心对称图形,又是轴对称图形.
【合作探究】
1.问题:用直尺和圆规作出正方形,正六多边形.
思考:如何作正三角形、正十二边形?
【自我检测】
1.正方形ABCD的外接圆圆心O叫做正方形ABCD的______.
2.正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______.
3.若正六边形的边长为1,那么正六边形的中心角是______度,半径是______,边心距是______,它的每一个内角是______.
4.正n边形的一个外角度数与它的______角的度数相等.
5.设一直角三角形的面积为8㎝2,两直角边长分别为x㎝和y㎝.
(1)写出y(㎝)和x(㎝)之间的函数关系式
(2)画出这个函数关系所对应的图象(3)根据图象,回答下列问题:
① 当x =2㎝时,y等于多少?
② x为何值时,这个直角三角形是等腰直角三角形?
6.已知三角形的两边长分别是方程 的两根,第三边的长是方程 的根,求这个三角形的周长.
7.如图,PA和PB分别与⊙O相切于A,B两点,作直径AC,并延长交PB于点D.连结OP,CB.
(1)求证:OP∥CB;
(2)若PA=12,DB:DC=2:1,求⊙O的半径.
8.如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0,)两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D.
(1)求直线AB的解析式;
(2)若S梯形OBCD=,求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似.
若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
9.如示意图,小华家(点A处)和公路( ( http: / / www.21cnjy.com ) )之间竖立着一块35m长且平行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路计为BC.一辆以60km/h匀速行驶的汽车经过公路段的时间是3s,已知广告牌和公路的距离是40m,求小华家岛公路的距离(精确到1m).
24.4.1弧长及扇形面积
(一)复习巩固:
1.圆与圆的五种位置关系: 、 、 、 、 .
2.已知两圆的半径分别3cm和2cm,若两圆没有公共点,则圆心距d的取值范围为( )
A. d>5或d<1 B. d>5 C. d<1 D.1<d<5
(二)新知导学
1.弧长计算公式
在半径为R的圆中,n0的圆心角所对的弧长l的计算公式为: l=
2.扇形面积计算公式
①定义: 叫做扇形.
②在半径为R的圆中,圆心角为n0的扇形面积的计算公式为:S扇形=
由弧长l= 和S扇形= 可得扇形面积计算的另一个公式为:
S扇形=
【合作探究】
1.已知:扇形的弧长为cm,面积为 cm2 ,求扇形弧所对的圆心角.
已知:AC是半圆的直径,BC与半圆切于C,AB交半圆于D,BC=3 cm BD= cm,
求半圆的面积.
【自我检测】
一、选择题
1.如果以扇形的半径为直径作一个圆,这个圆的面积恰好与已知扇形的面积相等,则已知扇形的中心角为( )
A.60° B.90° C.120° D.150°
2.如果圆柱底面直径为6cm,母线长为4cm,那么圆柱的侧面积为( )
A.24πcm2 B.36πcm2 C.12πcm2 D.48πcm2
3.圆锥的母线长为5cm,底面半径为3cm,则圆锥侧面展开图的面积是( )
A. πcm2 B.30πcm2 C.24πcm2 D.15πcm2
4.如果正四边形的边心距为2,那么这个正四边形的外接圆的半径等于( )
A.2 B.4 C. D.
5.圆的外切正六边形边长与它的内接正六边形边长的比为( )
A.:3 B. 2:3 C.3:3 D.:2
6.圆的半径为3cm,圆内接正三角形一边所对的弧长为( )
A.2πcm或4πcm B.2πcm C.4πcm D.6πcm
7.在半径为12cm的圆中,150°的圆心角所对的弧长等于( )
A.24πcm B.12πcm C.10πcm D.5πcm
8.如图, 设AB=1cm,,则长为( )
A. B. C. D.
9.圆锥的母线长为5cm,高为3cm,则其侧面展开图中,扇形的圆心角是( )
A.144° B.150° C.288° D.120°
二、计算题
10.如图,已知菱形ABCD中,AC,BD交于O点,AC=cm,BD=2cm,分别以 A,C为圆心,OA长为半径作弧,交菱形四边于E,F,G,H四点.求阴影部分的面积.
11.已知△ABC中,∠C=90°,AC=3cm,BC=4cm,⊙O内切于△ABC.求△ABC在⊙O外部的面积.
12.已知等腰梯形ABCD有一个内切圆O.若AB=CD=6cm,BC=2AD,求圆O的面积.
13.如图,ACBD为夹在环形的两条半径之间的一部分,弧AD的长为πcm,弧CB的长为2πcm,AC=4cm,求这个图形的面积.
14.已知如图,P是半径为R的⊙O外一 ( http: / / www.21cnjy.com )点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.求:夹在劣弧AB及PA,PB之间的阴影部分的面积.
15.已知扇形OAB的面积为S,∠AOB=60°.求扇形OAB的内切圆的面积.
三、证明
16.如图,已知同心⊙O中,外圆的面积是内圆 ( http: / / www.21cnjy.com )面积的2倍,外圆的弦AB,CD均与内圆相切,且AB∥CD.EFGH是内圆的内接正方形.求该圆环介于AB,CD间的面积等于正方形EFGH的面积.
17.已知直角三角形斜边上的高将原三角形分成两个直角三角形.求证这两个三角形的内切圆的面积的和等于原三角形的内切圆面积.
18.已知如图7-391,AB ( http: / / www.21cnjy.com )是半圆O的直径,C,D是半圆上两点,且弧AC=弧CD=弧DB,求证由弦AC及弧CD所围成的图形面积等于半圆面积的三分之一
19.若分别以线段CD的两个端点为 ( http: / / www.21cnjy.com )圆心,CD长为半径的⊙C,⊙D相交于A,B.求证分别以AB,CD为直径的两个圆的面积之和与⊙C的面积相等.
20.求证圆心角为60°的扇形的内切圆的面积,等于扇形面积的三分之二.
21.已知如图7-392,扇 ( http: / / www.21cnjy.com )形OAB中,OA⊥OB,分别以OA,OB为直径向形内作半圆,两圆弧交于C,求证由弧AC,弧BC,弧AB所围图形的面积与由弧OMC和弧ONC所围图形面积相等.
24.4.2圆锥的侧面积和全面积
【自主学习】
(一)复习巩固:
1.弧长的计算公式: .
2.扇形面积的计算公式: .
3.已知扇形的面积为4cm2,弧长为4cm,求扇形的半径.
(二)新知导学
1.圆锥的侧面展开图
圆锥的侧面展开图是一个 .
圆锥的母线就是扇形的 .
圆锥底面圆的周长就是扇形的 .
2.如果圆锥的母线长为l,底面的半径为r,那么
S侧= ,
S全= .
【合作探究】
1.已知圆锥的母线长6 cm;底面半径为 3 cm,求圆锥的侧面展开图中扇形的圆心角.
2.已知:一个圆锥的侧面展开图是圆心角为36°的扇形,扇形面积为10 cm2.求这圆锥的表面积.
【自我检测】
一、选择题
1.已知圆锥的高为,底面半径为2,则该圆锥侧面展开图的面积是( )
A.π B.2π C.π D.6π
2.圆锥的高为3cm , 母线长为5cm , 则它的表面积是( )cm2.
A.20p B.36p C.16p D.28p
3.已知圆锥的底面半径为3 , 母线长为12 ( http: / / www.21cnjy.com ) , 那么圆锥侧面展开图所成扇形的圆角为( )A.180° B.120° C.90° D.135°
4.如果圆锥的高与底面直径相等 , 则底面面积与侧面积之比为( )
A.1∶ B.2∶ C.∶ D.2∶3
5.边长为a的等边三角形 , 绕它一边上的高所在直线旋转180° , 所得几何体的表面积为( )A. B. C. D.π
6.若底面直径为6cm的圆锥的侧面展开图的圆心角为216°,则这个圆锥的高是( )cm.A.8 B. C.6 D.4
7.在一个边长为4cm正方形里作一个扇形(如图所示) , 再将这个扇形剪下
卷成一个圆锥的侧面 , 则这个圆锥的高为( )cm.
A. B. C. D.
8.用圆心角为120° , 半径为6cm的扇形围成圆锥的侧面 , 则这个圆锥的高为( )A.4 B.4 C.2 D.3
9.△ABC中 , AB=6cm , ∠A ( http: / / www.21cnjy.com )=30° , ∠B=15° , 则△ABC绕直线AC旋转一周所得几何体的表面积为( )cm2.
A.(18+9)π B.18+9
C.(36+18)π D.36+18
10.圆锥的母线长为10cm , 底面半径为3cm , 那么圆锥的侧面积为( )cm2.
A.30 B.30p C.60p D.15p
11.粮仓的顶部是圆锥形,这个圆锥的底面直径是4 m,母线长3 m,为防雨需在粮仓的顶部铺上油毡,那么这块油毡的面积至少为( )
A.6 m2 B.6πm2 C.12 m2 D.12πm2
12.若圆锥的侧面展开图是一个半径为a的半圆,则圆锥的高为( )
A.a B. C. D.
13.一个圆锥的高为cm,侧面展开图是一个半圆,则圆锥的全面积是( )
A.200πcm2 B.300πcm2 C.400πcm2 D.360πcm2
14.一个圆锥形的烟囱帽的侧面积为2000πcm2,母线长为50cm,那么这个烟囱帽的底面直径为( )
A.80cm B.100cm C.40cm D.5cm
二、填空题
15.已知圆锥的母线长是10cm,侧面展开图的面积是60πcm2,则这个圆锥的底面半径
是 cm.
16.已知圆锥的底面半径是2cm,母线长是5cm,则它的侧面积是 .
17.圆锥的轴截面是一个等边三角形,则这个圆锥的底面积、侧面积、全面积的比是 .
18.一个扇形,半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,那么这个圆锥的底面半径为 .
19.一个扇形,半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,那么这个圆锥的全面积为 .
三、解答题
20.一个圆锥形的零件,经过轴的剖面是一个等腰直角三角形,则它的侧面展开图扇形的圆心角是多少?
21.如图,一个圆柱的底面半径为40 cm,高为60 cm,从中挖去一个以圆柱上底为底、下底圆心为顶点的圆锥,得到一个几何体,求其全面积.
22.已知:一个圆锥的侧面积与表面积的比为2∶3.求这圆锥的锥角.
23.已知:一个圆锥的底半径 r=10cm,过轴的截面的顶角为60°.求它的侧面展开图的圆心角的度数及侧面积.
于是得到切线的性质定理:
圆的切线垂直于经过切点的半径.
几何语言为:∵ BC为⊙O的切线,切点为A
∴ BC⊥OA ( )
C
O
A
B
图4
·
A
B
C
D
O
M
第5题图
A
P
O
图2
A
P
O
图1
B
A
B
C
D
O
图3
E
第6-7题图
图1
图2
A
O
B
C
A
E
B
4
4
16
图1
A
C
E
D
B
O
图2
图1
图2
由此我们可以得到切线长定理:
从圆外一点引圆的两条 ,它们的 相等,这一点和圆心的连线平分两条切线的 .(记住)
几何语言为:∵ PA、PB是⊙O的切线,A、B为切点.
∴PA PB, .
1题图
2题图
3题图
4题图
2题图
; ;
1.悄悄告诉你:
eq \o\ac(○,1)一个正多边形的外接圆(或内切圆)的圆心叫这个正多边形的中心.
eq \o\ac(○,2)一个正多边形的外接圆的半径叫正多边形的半径.
eq \o\ac(○,3)正多边形每一条边所对的圆心角叫做正多边形的中心角.
eq \o\ac(○,4)中心到正多边形一边的距离叫做正多边形的边心距. 边心距也是正多边形内切圆的
2.考考你:
eq \o\ac(○,1)请你指出图中正多边形的中心 ;正多边形的半径 ;正多边形的中心角 ;
正多边形的边心距 ;
eq \o\ac(○,2)正三角形的中心角有 个,中心角的度数为 ;正四边形、正五边形、正六形呢?
……正n边形的中心角有 个,中心角的度数为 .
导学分析:
eq \o\ac(○,1)正六边形的中心角 ,所以 是等边三角形,
OC=OD= = m.所以正六边形的周长为 .
eq \o\ac(○,2)正六边形的边心距OM= .
正六边形ABCDEF的面积是 面积的 倍,
2题图
1题图
轻轻告诉你:
与三角形各边都相切的圆叫做三角形的内切圆(圆心叫做三角形的内心)
各边都与圆相切的三角形叫做圆的外切三角形
2题图
3题图
1题图
归纳总结:
(1)一个三角形有 个内切圆.
(2)一个圆有 个外切三角形.
(3)三角形的内心就是三角形 的交点.
(4)三角形的内心到三角形 的距离相等.
8题图
7题图
4题图
2题图
归纳总结:
(1)圆的周长公式 .
(2)弧长 的计算公式是 .(记住)
……
_
图
7
-
2
_
图
7
-
1
图8
图9
A
B
O
图12-1
A
B
O
图12-2
图11
图10
3题图
归纳总结:
(1)圆的面积公式为:
(2)即扇形的面积公式为: 或 .(记住)
C
B
A
O
F
D
E
第9题图
A
B
C
2题图
4题图
C
A
B
3题图
1题图
6题图
5题图
归纳总结:
1.圆锥的侧面展开图一个扇形,扇形的半径就是圆锥母线长 .扇形的弧长就是圆锥底面圆的周长 .
2.设圆锥的母线长为 ,底面圆的半径为r,则它的侧面积为 .
(记住会用)
20cm
30cm
图2
A
图3
图1
图2
图1
A
B
D
C
A
B
D(B)
(A)
(D)
C
A
D
B
C
l
A
C
O
B
10题图
O
B
A
·
图10—2
图10—1
A
B
2米
4 米
(4)图
A
P
O
第8题图
第9题图
第11题图
第12题图
第5题图
第6题图
第9题图
A
M
O
B
P
M
A
N
E
D
O
图(1)
.
M
A
N
E
D
B
C
O
图(2)
同课章节目录
