人教版数学八年级上册 11.2.1 三角形的内角 导学案(含答案)
文档属性
| 名称 | 人教版数学八年级上册 11.2.1 三角形的内角 导学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 168.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 10:29:46 | ||
图片预览

文档简介
11.2 与三角形有关的角
11.2.1 三角形的内角
学习目标
1.掌握三角形的内角和定理及其推论.
2.理解三角形的内角和定理的推导、验证过程.
3.会运用三角形的内角和及直角三角形的性质和判定进行相关计算.
学习策略
1.通过动手拼图掌握三角形内角和定理的证明方法;
2.牢记三角形三角形的内角和180°和推论,应用其进行相关的计算.
学习过程
一.复习回顾:
1.三角形具有什么性质?
稳定性
2. 小学的时候我们通过测量或者剪拼得出三角形的内角和等于多少度?
180°
二.新课学习:
知识点一:三角形内角和定理
1.作如图1所示的辅助线,证明三角形的内角和定理,试完成如下证明过程:
作CD∥AB,则∠A= (两直线平行, ),
∠B+ =180°(两直线平行, ),
∴∠A+∠B+∠ACB= (等式的性质).
【答案】∠ACD,内错角相等,∠BCD,同旁内角互补,180°.
2.三角形内角和最直接的一个应用是已知三角形的两个角求第三个角,可直接用 减去已知两角的度数即可.
综上:三角形的内角和等于 ,证明时常通过添加 构造平角、同旁内角建立起三个角之间的关系.在△ABC中,若已知∠A、∠B,则∠C= .
【答案】180°,180°,平行线,180°-∠A-∠B.
知识点二:三角形内角和定理的实际应用
阅读课本“例2”,解决下列问题.
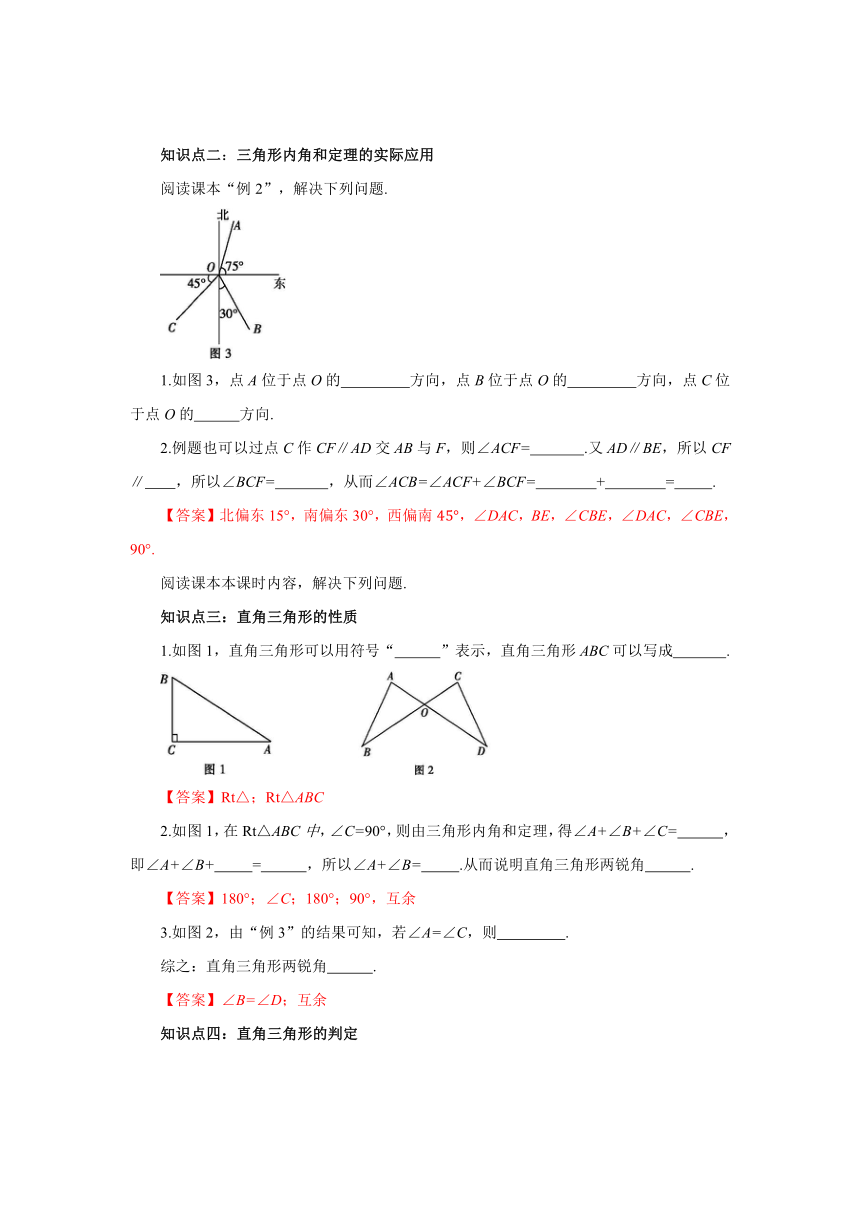
1.如图3,点A位于点O的 方向,点B位于点O的 方向,点C位于点O的 方向.
2.例题也可以过点C作CF∥AD交AB与F,则∠ACF= .又AD∥BE,所以CF∥ ,所以∠BCF= ,从而∠ACB=∠ACF+∠BCF= + = .
【答案】北偏东15°,南偏东30°,西偏南,∠DAC,BE,∠CBE,∠DAC,∠CBE,90°.
阅读课本本课时内容,解决下列问题.
知识点三:直角三角形的性质
1.如图1,直角三角形可以用符号“ ”表示,直角三角形ABC可以写成 .
【答案】Rt△;Rt△ABC
2.如图1,在Rt△ABC中,∠C=90°,则由三角形内角和定理,得∠A+∠B+∠C= ,即∠A+∠B+ = ,所以∠A+∠B= .从而说明直角三角形两锐角 .
【答案】180°;∠C;180°;90°,互余
3.如图2,由“例3”的结果可知,若∠A=∠C,则 .
综之:直角三角形两锐角 .
【答案】∠B=∠D;互余
知识点四:直角三角形的判定
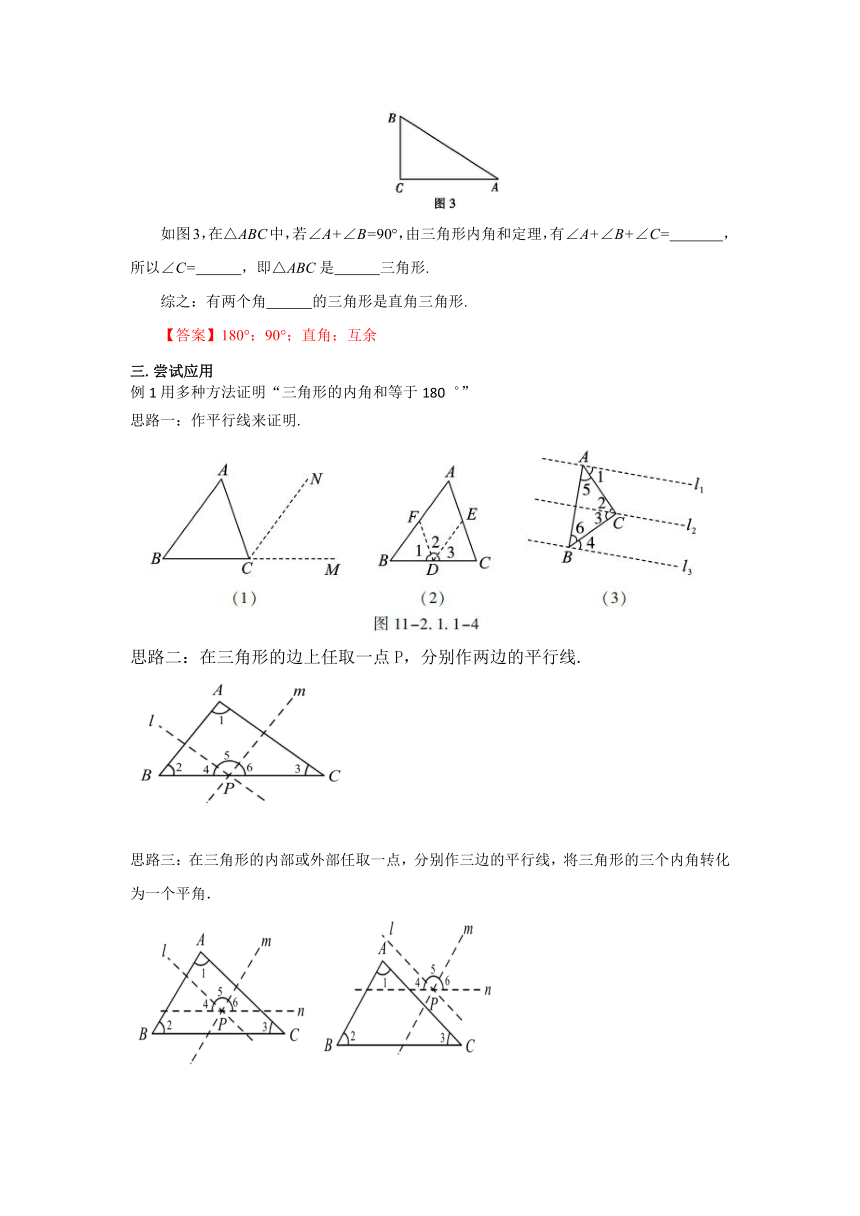
如图3,在△ABC中,若∠A+∠B=90°,由三角形内角和定理,有∠A+∠B+∠C= ,所以∠C= ,即△ABC是 三角形.
综之:有两个角 的三角形是直角三角形.
【答案】180°;90°;直角;互余
三.尝试应用
例1用多种方法证明“三角形的内角和等于180 ”
思路一:作平行线来证明.
思路二:在三角形的边上任取一点P,分别作两边的平行线.
思路三:在三角形的内部或外部任取一点,分别作三边的平行线,将三角形的三个内角转化为一个平角.
例2如图,在△ABC 中,∠ABC= 70°,∠C=65°,BD⊥AC于D,求∠ABD,∠CBD的度数.
解:∵∠ABC = 70°,∠C = 65°,
∴∠A = 180°–∠ABC –∠C = 45°.
∵BD⊥AC,
∴∠ADB =∠CDB = 90°,
∴∠ABD = 90°–∠A = ∠45°,
∠CBD = 90° – ∠C = 25°.
四.自主总结:
1.三角形内角和等于______________; 180
2.直角三角形的两锐角____________; 互余
3. 有两个角 的三角形是直角三角形. 互余
五、达标测试
一、选择题
1. 如图是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( )
A.30° B.40° C.50° D.60°
2.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
3. 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
A.40° B.50° C.60° D.70°
4. 若CD平分含30°角的三角板的∠ACB,则∠1等于( )
A.110° B.105° C.100° D.95°
5.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3 D.∠A=∠B=3∠C
二、填空题
6.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是_______.
7.已知:如图,在△ABC中,∠A=55°,F是高BE、CD的交点,则∠BFC=________.
8.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=______度.
第6题图 第7题图 第8题图
9.直角三角形的一个锐角是另一个锐角的4倍,那么这个锐角的度数是( )
三、解答题:
10. 如图,在△ABC中,∠C=90°,AD平分∠BAC,且∠B=3∠BAD,求∠ADC的度数.
参考答案
1. B解析:∵△ABC中,∠A=100°,∠B=40°,∴∠C=180°-∠A-∠B=180°-100°-40°=40°.故选B.
2. D 解析:∵∠A=20°,∠B=60°,∴∠C=180°-∠A-∠B=180°-20°-60°=100°,
∴△ABC是钝角三角形.故选:D.
3. A解析:∵AB⊥BD,∠A=40°,∴∠AEB=50°,∴∠DEC=50°,又AC⊥CD,
∴∠D=40°,故选:A.
4. B 解析:∵∠ACB=90°,CD平分∠ACB,∴∠DCB=45°,
∵∠A=30°,∴∠B=60°,∴∠1=∠B+∠DCB=60°+45°=105°,故选B.
5. D解:A选项,∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,不符合题意;B选项,∠A-∠B=∠C,即2∠A=180°,∠A=90°,为直角三角形,不符合题意;C选项,∠A:∠B:∠C=1:2:3,即∠A+∠B=∠C,同A选项,不符合题意;D选项,∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,符合题意.故选:D.
6.85°解析:∵在△ABC中,∠A=50°,∠ABC=70°,∴∠C=60°,∵BD平分∠ABC,∴∠DBC=35°,∴∠BDC=180°-60°-35°=85°.
7.125° 解析:∵∠A=55°,BE⊥AC,CD⊥AB,∴∠ABE=∠ACD=180°-∠A-90°=35°,∴∠BCF+∠CBF=180°-∠A-∠ABE-∠ACD=180°-55°-35°-35°=55°,∵∠BFC+∠BCF+∠CBF=180°,∴∠BFC=125°.
8.70解析:∵AB∥CD,∴∠EFD=180-∠FEB;∵EP⊥EF,与∠EFD的平分线FP相交于点P,∴∠EFD=180°-50°-90°=40°,∴∠EFP=20°;∴∠EPF=180°-90°-20°=70°.
9. 设这个锐角度数是x,则另一个锐角度数是(90-x)°,
由题意得,x=4(90-x),解得x=72°,所以,这个锐角的度数是72°.
10. 解:∵AD平分∠BAC,∴∠BAD=∠BAC,∵∠BAC+∠B+∠C=180°,而∠B=3∠BAD,∴2∠BAD+3∠BAD+90°=180°,∴∠BAD=18°,∴∠B=3∠BAD=54°,∴∠ADC=∠BAD+∠B=18°+54°=72°.
11.2.1 三角形的内角
学习目标
1.掌握三角形的内角和定理及其推论.
2.理解三角形的内角和定理的推导、验证过程.
3.会运用三角形的内角和及直角三角形的性质和判定进行相关计算.
学习策略
1.通过动手拼图掌握三角形内角和定理的证明方法;
2.牢记三角形三角形的内角和180°和推论,应用其进行相关的计算.
学习过程
一.复习回顾:
1.三角形具有什么性质?
稳定性
2. 小学的时候我们通过测量或者剪拼得出三角形的内角和等于多少度?
180°
二.新课学习:
知识点一:三角形内角和定理
1.作如图1所示的辅助线,证明三角形的内角和定理,试完成如下证明过程:
作CD∥AB,则∠A= (两直线平行, ),
∠B+ =180°(两直线平行, ),
∴∠A+∠B+∠ACB= (等式的性质).
【答案】∠ACD,内错角相等,∠BCD,同旁内角互补,180°.
2.三角形内角和最直接的一个应用是已知三角形的两个角求第三个角,可直接用 减去已知两角的度数即可.
综上:三角形的内角和等于 ,证明时常通过添加 构造平角、同旁内角建立起三个角之间的关系.在△ABC中,若已知∠A、∠B,则∠C= .
【答案】180°,180°,平行线,180°-∠A-∠B.
知识点二:三角形内角和定理的实际应用
阅读课本“例2”,解决下列问题.
1.如图3,点A位于点O的 方向,点B位于点O的 方向,点C位于点O的 方向.
2.例题也可以过点C作CF∥AD交AB与F,则∠ACF= .又AD∥BE,所以CF∥ ,所以∠BCF= ,从而∠ACB=∠ACF+∠BCF= + = .
【答案】北偏东15°,南偏东30°,西偏南,∠DAC,BE,∠CBE,∠DAC,∠CBE,90°.
阅读课本本课时内容,解决下列问题.
知识点三:直角三角形的性质
1.如图1,直角三角形可以用符号“ ”表示,直角三角形ABC可以写成 .
【答案】Rt△;Rt△ABC
2.如图1,在Rt△ABC中,∠C=90°,则由三角形内角和定理,得∠A+∠B+∠C= ,即∠A+∠B+ = ,所以∠A+∠B= .从而说明直角三角形两锐角 .
【答案】180°;∠C;180°;90°,互余
3.如图2,由“例3”的结果可知,若∠A=∠C,则 .
综之:直角三角形两锐角 .
【答案】∠B=∠D;互余
知识点四:直角三角形的判定
如图3,在△ABC中,若∠A+∠B=90°,由三角形内角和定理,有∠A+∠B+∠C= ,所以∠C= ,即△ABC是 三角形.
综之:有两个角 的三角形是直角三角形.
【答案】180°;90°;直角;互余
三.尝试应用
例1用多种方法证明“三角形的内角和等于180 ”
思路一:作平行线来证明.
思路二:在三角形的边上任取一点P,分别作两边的平行线.
思路三:在三角形的内部或外部任取一点,分别作三边的平行线,将三角形的三个内角转化为一个平角.
例2如图,在△ABC 中,∠ABC= 70°,∠C=65°,BD⊥AC于D,求∠ABD,∠CBD的度数.
解:∵∠ABC = 70°,∠C = 65°,
∴∠A = 180°–∠ABC –∠C = 45°.
∵BD⊥AC,
∴∠ADB =∠CDB = 90°,
∴∠ABD = 90°–∠A = ∠45°,
∠CBD = 90° – ∠C = 25°.
四.自主总结:
1.三角形内角和等于______________; 180
2.直角三角形的两锐角____________; 互余
3. 有两个角 的三角形是直角三角形. 互余
五、达标测试
一、选择题
1. 如图是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为( )
A.30° B.40° C.50° D.60°
2.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
3. 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
A.40° B.50° C.60° D.70°
4. 若CD平分含30°角的三角板的∠ACB,则∠1等于( )
A.110° B.105° C.100° D.95°
5.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A-∠B=∠C
C.∠A:∠B:∠C=1:2:3 D.∠A=∠B=3∠C
二、填空题
6.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是_______.
7.已知:如图,在△ABC中,∠A=55°,F是高BE、CD的交点,则∠BFC=________.
8.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=______度.
第6题图 第7题图 第8题图
9.直角三角形的一个锐角是另一个锐角的4倍,那么这个锐角的度数是( )
三、解答题:
10. 如图,在△ABC中,∠C=90°,AD平分∠BAC,且∠B=3∠BAD,求∠ADC的度数.
参考答案
1. B解析:∵△ABC中,∠A=100°,∠B=40°,∴∠C=180°-∠A-∠B=180°-100°-40°=40°.故选B.
2. D 解析:∵∠A=20°,∠B=60°,∴∠C=180°-∠A-∠B=180°-20°-60°=100°,
∴△ABC是钝角三角形.故选:D.
3. A解析:∵AB⊥BD,∠A=40°,∴∠AEB=50°,∴∠DEC=50°,又AC⊥CD,
∴∠D=40°,故选:A.
4. B 解析:∵∠ACB=90°,CD平分∠ACB,∴∠DCB=45°,
∵∠A=30°,∴∠B=60°,∴∠1=∠B+∠DCB=60°+45°=105°,故选B.
5. D解:A选项,∠A+∠B=∠C,即2∠C=180°,∠C=90°,为直角三角形,不符合题意;B选项,∠A-∠B=∠C,即2∠A=180°,∠A=90°,为直角三角形,不符合题意;C选项,∠A:∠B:∠C=1:2:3,即∠A+∠B=∠C,同A选项,不符合题意;D选项,∠A=∠B=3∠C,即7∠C=180°,三个角没有90°角,故不是直角三角形,符合题意.故选:D.
6.85°解析:∵在△ABC中,∠A=50°,∠ABC=70°,∴∠C=60°,∵BD平分∠ABC,∴∠DBC=35°,∴∠BDC=180°-60°-35°=85°.
7.125° 解析:∵∠A=55°,BE⊥AC,CD⊥AB,∴∠ABE=∠ACD=180°-∠A-90°=35°,∴∠BCF+∠CBF=180°-∠A-∠ABE-∠ACD=180°-55°-35°-35°=55°,∵∠BFC+∠BCF+∠CBF=180°,∴∠BFC=125°.
8.70解析:∵AB∥CD,∴∠EFD=180-∠FEB;∵EP⊥EF,与∠EFD的平分线FP相交于点P,∴∠EFD=180°-50°-90°=40°,∴∠EFP=20°;∴∠EPF=180°-90°-20°=70°.
9. 设这个锐角度数是x,则另一个锐角度数是(90-x)°,
由题意得,x=4(90-x),解得x=72°,所以,这个锐角的度数是72°.
10. 解:∵AD平分∠BAC,∴∠BAD=∠BAC,∵∠BAC+∠B+∠C=180°,而∠B=3∠BAD,∴2∠BAD+3∠BAD+90°=180°,∴∠BAD=18°,∴∠B=3∠BAD=54°,∴∠ADC=∠BAD+∠B=18°+54°=72°.
