角平分线第二课时[下学期]
文档属性
| 名称 | 角平分线第二课时[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 64.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-13 20:10:00 | ||
图片预览


文档简介
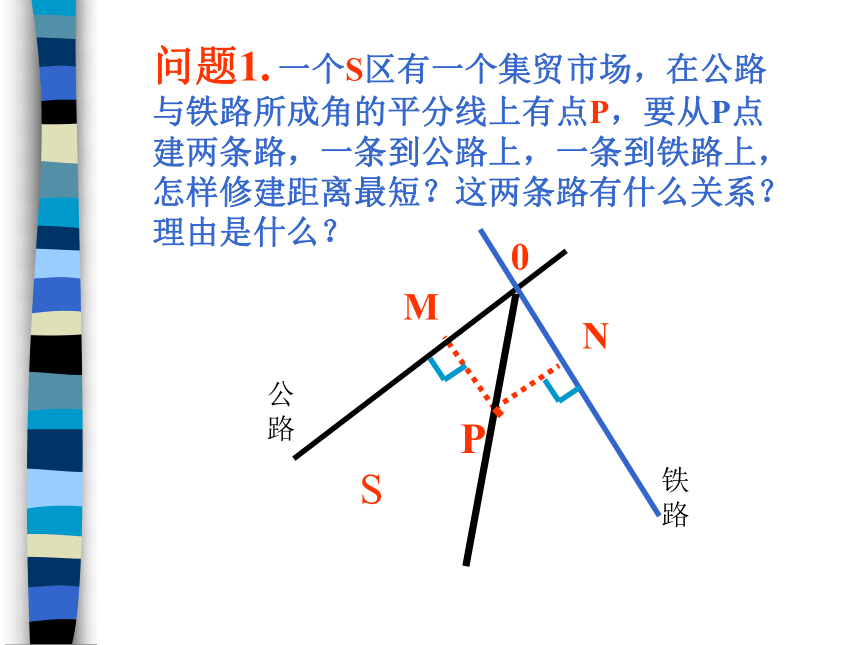
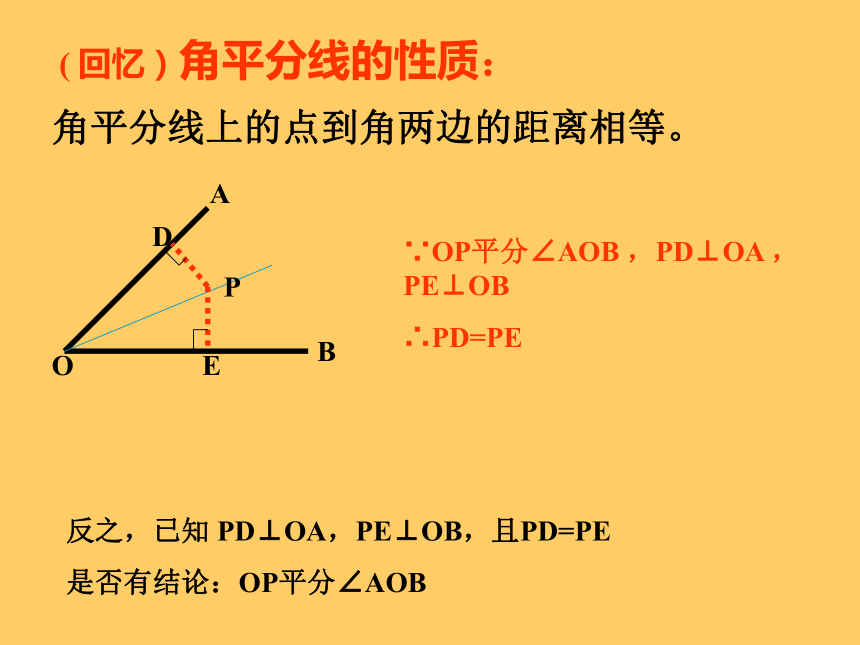
课件12张PPT。角平分线(二)洪家二中 盛婉君问题1. 一个S区有一个集贸市场,在公路与铁路所成角的平分线上有点P,要从P点建两条路,一条到公路上,一条到铁路上,怎样修建距离最短?这两条路有什么关系?理由是什么?铁路( 回忆)角平分线的性质:角平分线上的点到角两边的距离相等。∵OP平分∠AOB ,PD⊥OA , PE⊥OB
∴PD=PE反之,已知 PD⊥OA,PE⊥OB,且PD=PE
是否有结论:OP平分∠AOB已知: PD⊥OA,PE⊥OB,且PD=PE求证:OP平分∠AOB证明:∵PD⊥OA,PE⊥OB∴∠ODP=∠OEP=90°∵在Rt△ODP和Rt△OEP中
OP=OP PD=PE
∴Rt△ODP≌Rt△OEP(HL)∴∠DOP=∠EOP∴OP平分∠AOB逆定理:
到角两边距离相等的点在这个角的平分线上。∵PD⊥OA,PE⊥OB,且PD=PE
∴OP平分∠AOB几何式子:练习:
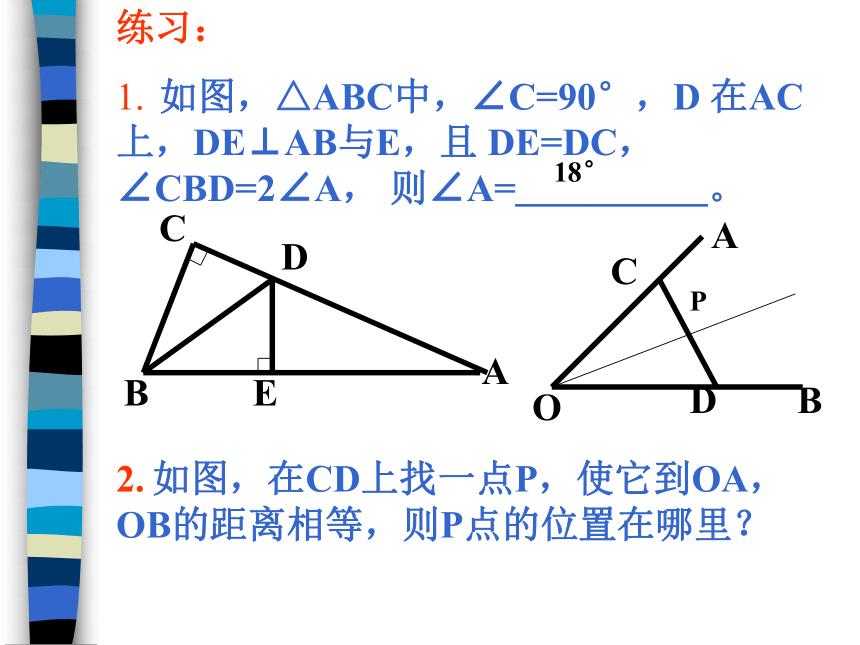
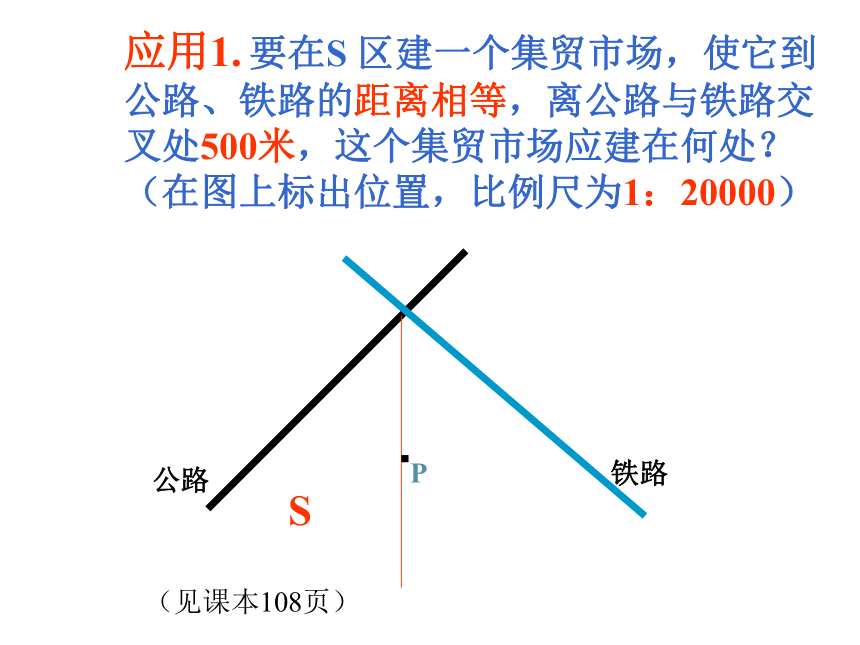
1. 如图,△ABC中,∠C=90°,D 在AC 上,DE⊥AB与E,且 DE=DC,∠CBD=2∠A, 则∠A=_____。2. 如图,在CD上找一点P,使它到OA,OB的距离相等,则P点的位置在哪里?18°P应用1. 要在S 区建一个集贸市场,使它到公路、铁路的距离相等,离公路与铁路交叉处500米,这个集贸市场应建在何处?(在图上标出位置,比例尺为1:20000)(见课本108页)P问题2. 画△ABC,作出两角的平分线,观察交点P到这个三角形三边的距离,你发现了什么?E结论
(1)三角形两角平分线的交点到三边的距离相等。(2)点P在∠BAC的角平分线上。(3)三角形三条角平分线交于一点。应用2. 要在A区建一个货物中转站,使它到三条公路的距离相等,请问:中转站应建在何处?到三角形三边距离相等的点,就是角平分线的交点。问题3. 将上题中的两条内角平分线改为两条外角平分线,这时结论会有变化吗?E应用3. 如图, a,b,c 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?c再见
∴PD=PE反之,已知 PD⊥OA,PE⊥OB,且PD=PE
是否有结论:OP平分∠AOB已知: PD⊥OA,PE⊥OB,且PD=PE求证:OP平分∠AOB证明:∵PD⊥OA,PE⊥OB∴∠ODP=∠OEP=90°∵在Rt△ODP和Rt△OEP中
OP=OP PD=PE
∴Rt△ODP≌Rt△OEP(HL)∴∠DOP=∠EOP∴OP平分∠AOB逆定理:
到角两边距离相等的点在这个角的平分线上。∵PD⊥OA,PE⊥OB,且PD=PE
∴OP平分∠AOB几何式子:练习:
1. 如图,△ABC中,∠C=90°,D 在AC 上,DE⊥AB与E,且 DE=DC,∠CBD=2∠A, 则∠A=_____。2. 如图,在CD上找一点P,使它到OA,OB的距离相等,则P点的位置在哪里?18°P应用1. 要在S 区建一个集贸市场,使它到公路、铁路的距离相等,离公路与铁路交叉处500米,这个集贸市场应建在何处?(在图上标出位置,比例尺为1:20000)(见课本108页)P问题2. 画△ABC,作出两角的平分线,观察交点P到这个三角形三边的距离,你发现了什么?E结论
(1)三角形两角平分线的交点到三边的距离相等。(2)点P在∠BAC的角平分线上。(3)三角形三条角平分线交于一点。应用2. 要在A区建一个货物中转站,使它到三条公路的距离相等,请问:中转站应建在何处?到三角形三边距离相等的点,就是角平分线的交点。问题3. 将上题中的两条内角平分线改为两条外角平分线,这时结论会有变化吗?E应用3. 如图, a,b,c 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有几处?c再见
