13.1.1轴对称同步训练(含答案)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 13.1.1轴对称同步训练(含答案)2023-2024学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 418.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览



文档简介
13.1.1轴对称同步训练2023-2024学年人教版数学八年级上册
一、单选题
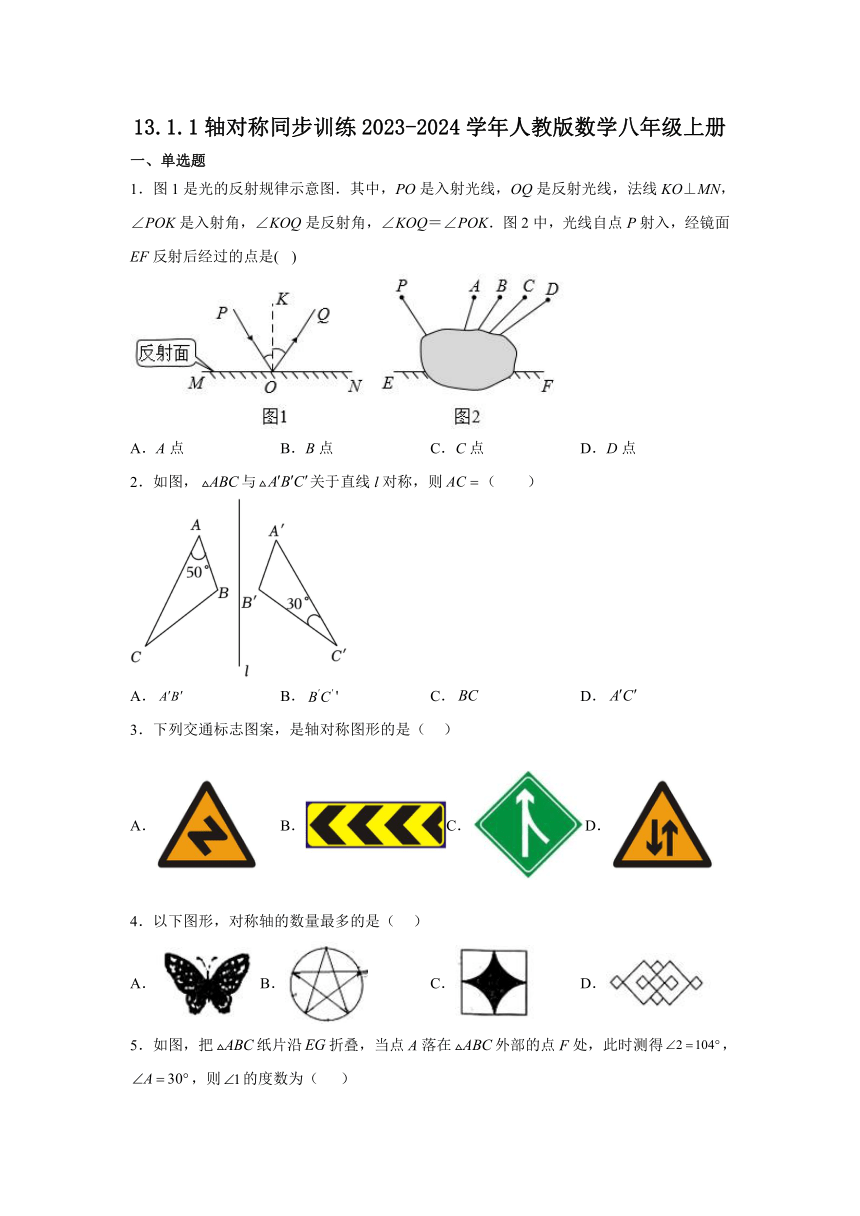
1.图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
A.A点 B.B点 C.C点 D.D点
2.如图,与关于直线l对称,则( )
A. B.' C. D.
3.下列交通标志图案,是轴对称图形的是( )
A. B.C. D.
4.以下图形,对称轴的数量最多的是( )
A.B. C. D.
5.如图,把纸片沿折叠,当点A落在外部的点F处,此时测得,,则的度数为( )
A. B. C. D.
6.如图,直线是三角形的对称轴,点E,F是AD上的两点,若,,则图中阴影部分的面积是( )
A.1 B.3 C.6 D.9
7.下列说法中,正确结论的个数为( )
(1)有两边对应相等的两个直角三角形全等;(2)有一角为50°,且腰长相等的两个等腰三角形全等;(3)全等的两个图形一定关于某一条直线对称;(4)如果点M与N到直线l的距离相等,那么点M与点N关于直线l对称.
A.4个 B.3个 C.2个 D.1个
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,D,E,F分别是AB,BC,AC边上的动点,则△DEF的周长的最小值是( )
A.2.5 B.3.5 C.4.8 D.6
二、填空题
9.下列说法:①任意两条相交直线都组成一个轴对称图形;②等腰三角形最少有条对称轴,最多有条对称轴;③成轴对称的两个三角形一定全等;④全等的两个三角形一定成轴对称.其中正确的有 .(填序号)
10.如图,内有一点P,点P关于的轴对称点是G,点P关于的轴对称点是H,分别交、于A、B点,若,则= .
11.△ABC与关于直线l对称,则∠B的度数为 .
12.根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为,光线n与光线k的夹角的度数为.则x与y之间的数量关系是 .
13.如图,点D是锐角内一点,于点E,点F是线段的一个动点,点G是射线的一个动点,连接、、,当的周长最小时,与的数量关系式是 .
三、解答题
14.如图,和关于直线对称,已知,,.求的度数及、的长度.
15.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=1cm,∠BAC=76°,∠EAC=58°.
(1)求出BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?
16.如图,点E,F分别在的边,上,将沿折叠,点B落在点D的位置,与交于点M.写出,,间的数量关系,并证明你的结论.
17.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
参考答案
1--8BDBBB BDC
9.①②③
10.
11.
12.
13.
14.解:和关于直线对称,
,,,
又,,.
,,,
15.(1)解:∵△ABC与△ADE关于直线MN对称,ED=4cm,FC=1cm,
∴BC=ED=4cm,
∴BF=BC﹣FC=3cm.
(2)解:∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°.
(3)解:直线MN垂直平分线段EC.理由如下:如图,
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
16.解:在中,,
在中,,
∵由沿折叠所得,
∴,
∴.
17.()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵ ,
∴ △ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
一、单选题
1.图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
A.A点 B.B点 C.C点 D.D点
2.如图,与关于直线l对称,则( )
A. B.' C. D.
3.下列交通标志图案,是轴对称图形的是( )
A. B.C. D.
4.以下图形,对称轴的数量最多的是( )
A.B. C. D.
5.如图,把纸片沿折叠,当点A落在外部的点F处,此时测得,,则的度数为( )
A. B. C. D.
6.如图,直线是三角形的对称轴,点E,F是AD上的两点,若,,则图中阴影部分的面积是( )
A.1 B.3 C.6 D.9
7.下列说法中,正确结论的个数为( )
(1)有两边对应相等的两个直角三角形全等;(2)有一角为50°,且腰长相等的两个等腰三角形全等;(3)全等的两个图形一定关于某一条直线对称;(4)如果点M与N到直线l的距离相等,那么点M与点N关于直线l对称.
A.4个 B.3个 C.2个 D.1个
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,D,E,F分别是AB,BC,AC边上的动点,则△DEF的周长的最小值是( )
A.2.5 B.3.5 C.4.8 D.6
二、填空题
9.下列说法:①任意两条相交直线都组成一个轴对称图形;②等腰三角形最少有条对称轴,最多有条对称轴;③成轴对称的两个三角形一定全等;④全等的两个三角形一定成轴对称.其中正确的有 .(填序号)
10.如图,内有一点P,点P关于的轴对称点是G,点P关于的轴对称点是H,分别交、于A、B点,若,则= .
11.△ABC与关于直线l对称,则∠B的度数为 .
12.根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为,光线n与光线k的夹角的度数为.则x与y之间的数量关系是 .
13.如图,点D是锐角内一点,于点E,点F是线段的一个动点,点G是射线的一个动点,连接、、,当的周长最小时,与的数量关系式是 .
三、解答题
14.如图,和关于直线对称,已知,,.求的度数及、的长度.
15.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED=4cm,FC=1cm,∠BAC=76°,∠EAC=58°.
(1)求出BF的长度;
(2)求∠CAD的度数;
(3)连接EC,线段EC与直线MN有什么关系?
16.如图,点E,F分别在的边,上,将沿折叠,点B落在点D的位置,与交于点M.写出,,间的数量关系,并证明你的结论.
17.如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
参考答案
1--8BDBBB BDC
9.①②③
10.
11.
12.
13.
14.解:和关于直线对称,
,,,
又,,.
,,,
15.(1)解:∵△ABC与△ADE关于直线MN对称,ED=4cm,FC=1cm,
∴BC=ED=4cm,
∴BF=BC﹣FC=3cm.
(2)解:∵△ABC与△ADE关于直线MN对称,∠BAC=76°,∠EAC=58°,
∴∠EAD=∠BAC=76°,
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°.
(3)解:直线MN垂直平分线段EC.理由如下:如图,
∵E,C关于直线MN对称,
∴直线MN垂直平分线段EC.
16.解:在中,,
在中,,
∵由沿折叠所得,
∴,
∴.
17.()证明:∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
在△ABD和△ACD′中,
∵ ,
∴ △ABD≌△ACD′(SSS).
()解:∵≌,
∴,
∴,
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
∴,
即.
