22.1.3 二次函数y=a(x-h)?+k的图象和性质(第2课时) 课件(共19张PPT)
文档属性
| 名称 | 22.1.3 二次函数y=a(x-h)?+k的图象和性质(第2课时) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
人教九上数学同步精品课件
人教版九年级上册
22.1.3 二次函数y=a(x-h)2+k的图象和性质(第2课时)
学习目标
1.掌握二次函数y=a(x-h)2+k(a≠0)的图象的性质.
2.利用二次函数y=a(x-h)2+k(a≠0)解决实际问题.
y=a(x-h)2+k a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
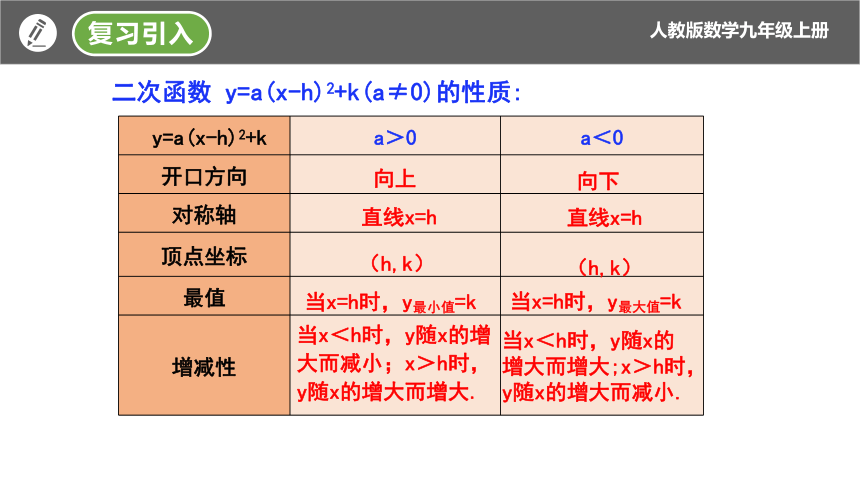
二次函数 y=a(x-h)2+k(a≠0)的性质:
复习引入
向上
直线x=h
(h,k)
当x=h时,y最小值=k
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
向下
当x=h时,y最大值=k
当x<h时,y随x的增大而增大;x>h时,y随x的增大而减小.
直线x=h
(h,k)
典例精析
例4 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长
(1,3)
y/m
O 1 2 3 x/m
3
2
1
解:如图,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是
y=a(x-1)2+3 (0≤x≤3).
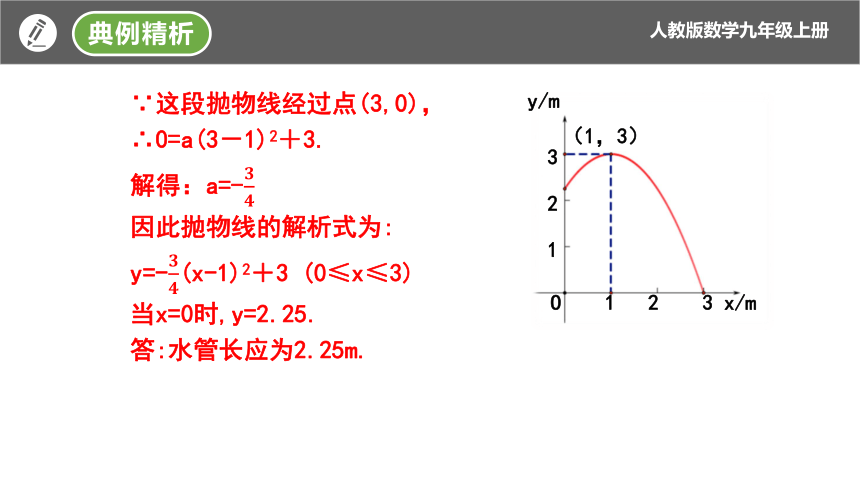
∵这段抛物线经过点(3,0),
∴0=a(3-1)2+3.
解得:a=-
因此抛物线的解析式为:
y=-(x-1)2+3 (0≤x≤3)
当x=0时,y=2.25.
答:水管长应为2.25m.
(1,3)
y/m
O 1 2 3 x/m
3
2
1
典例精析
例5 如图,已知抛物线y=a(x-h)2+k与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),对称轴为直线x=1.
(1)求抛物线对应的函数解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
解:(1)由题意可知h=1,则y=a(x-1)2+k.将点(3,0),(0,3)的坐标代入上式,得:
故抛物线对应的函数解析式为y=-(x-1)2+4.
解得
典例精析
(2)①当MA=MB时,M(0,0);
②当AB=AM时,M(0,-3);
③当AB=BM时,M(0,3+ )
或M(0,3- ).
所以点M的坐标为(0,0),(0,-3),
(0,3+ )或(0,3- ).
典例精析
1.设抛物线C1:y=x2向右平移2个单位长度,向下平移3个单位
长度得到抛物线C2,则抛物线C2对应的函数解析式是( )
A.y=(x-2)2-3 B.y=(x+2)2-3
C.y=(x-2)2+3 D.y=(x+2)2+3
2.将抛物线y=x2+1先向左平移2个单位长度,再向下平移3个单位长度,所得抛物线对应的函数解析式是( )
A.y=(x+2)2+2 B.y=(x+2)2-2
C.y=(x-2)2+2 D.y=(x-2)2-2
A
B
小试牛刀
3.二次函数y=(x+2)2-1的图象大致为( )
4.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或-5 B.-1或5
C.1或-3 D.1或3
D
B
小试牛刀
1.二次函数y=2(x-5)2+3的图象的顶点坐标是( )
A.(-5,3) B.(5,3) C.(5,-3) D.(-5,-3)
2.已知二次函数y=2(x-3)2+1,下列说法:①其图象开口向下;②其图象的对称轴为直线x=-3;③当x=3时,函数有最大值1;④当x<3时,y随x增大而减小其中正确说法的个数是( )
A.1 B.2 C.3 D.4
3.如图,平面直角坐标系中,两条抛物线有
相同的对称轴,则下列关系正确的是( )
A.m=n,k>h B.m=n,kC.m>n,k=h D.mB
A
A
课堂检测
4.某广场中心有高低不同的各种喷泉,其中一支高度为1m的喷水管喷出的抛物线型水柱最大高度为3m,此时距喷水管的水平距离为 m,求在如图所示的平面直角坐标系中抛物线型水柱对应的函数解析式(不要求写出自变量的取值范围).
课堂检测
解:∵点( ,3)是抛物线的顶点,
∴可设抛物线型水柱对应的函数解析式为
y=a(x- )2+3.
∵抛物线经过点(0,1),
∴1=(0- )2 a+3,解得a=-8.
∴抛物线型水柱对应的函数解析式为:
y=-8(x- )2+3.
课堂检测
1.如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积的最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
C
拓展训练
1.利用二次函数解决实际问题中的喷水问题.
2.利用二次函数解决实际问题中的几何图形问题.
课堂小结
1.若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x-2)2+3 C.y=(x+2)2-3 D.y=(x-2)2-3
2.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________.
3.若y=x2+(k-2)的顶点是原点,则k____;
若顶点位于x轴上方,则k____;
若顶点位于x轴下方,则k .
B
y=-3(x-2)2+3
=2
>2
<2
课后作业
4.若函数y=3(x-4)2+k与x轴的一个交点坐标是(2,0),
则它与x轴的另一个交点坐标是 .
5.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-1)2+1的
图象上,若x1>x2>1,则y1 y2(填“>”“=”“<”).
(6,0)
>
课后作业
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
22.1.3 二次函数y=a(x-h)2+k的图象和性质(第2课时)
学习目标
1.掌握二次函数y=a(x-h)2+k(a≠0)的图象的性质.
2.利用二次函数y=a(x-h)2+k(a≠0)解决实际问题.
y=a(x-h)2+k a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
二次函数 y=a(x-h)2+k(a≠0)的性质:
复习引入
向上
直线x=h
(h,k)
当x=h时,y最小值=k
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
向下
当x=h时,y最大值=k
当x<h时,y随x的增大而增大;x>h时,y随x的增大而减小.
直线x=h
(h,k)
典例精析
例4 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长
(1,3)
y/m
O 1 2 3 x/m
3
2
1
解:如图,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,水管所在直线为y轴,建立直角坐标系.
点(1,3)是图中这段抛物线的顶点.
因此可设这段抛物线对应的函数是
y=a(x-1)2+3 (0≤x≤3).
∵这段抛物线经过点(3,0),
∴0=a(3-1)2+3.
解得:a=-
因此抛物线的解析式为:
y=-(x-1)2+3 (0≤x≤3)
当x=0时,y=2.25.
答:水管长应为2.25m.
(1,3)
y/m
O 1 2 3 x/m
3
2
1
典例精析
例5 如图,已知抛物线y=a(x-h)2+k与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),对称轴为直线x=1.
(1)求抛物线对应的函数解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标.
解:(1)由题意可知h=1,则y=a(x-1)2+k.将点(3,0),(0,3)的坐标代入上式,得:
故抛物线对应的函数解析式为y=-(x-1)2+4.
解得
典例精析
(2)①当MA=MB时,M(0,0);
②当AB=AM时,M(0,-3);
③当AB=BM时,M(0,3+ )
或M(0,3- ).
所以点M的坐标为(0,0),(0,-3),
(0,3+ )或(0,3- ).
典例精析
1.设抛物线C1:y=x2向右平移2个单位长度,向下平移3个单位
长度得到抛物线C2,则抛物线C2对应的函数解析式是( )
A.y=(x-2)2-3 B.y=(x+2)2-3
C.y=(x-2)2+3 D.y=(x+2)2+3
2.将抛物线y=x2+1先向左平移2个单位长度,再向下平移3个单位长度,所得抛物线对应的函数解析式是( )
A.y=(x+2)2+2 B.y=(x+2)2-2
C.y=(x-2)2+2 D.y=(x-2)2-2
A
B
小试牛刀
3.二次函数y=(x+2)2-1的图象大致为( )
4.已知二次函数y=(x-h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或-5 B.-1或5
C.1或-3 D.1或3
D
B
小试牛刀
1.二次函数y=2(x-5)2+3的图象的顶点坐标是( )
A.(-5,3) B.(5,3) C.(5,-3) D.(-5,-3)
2.已知二次函数y=2(x-3)2+1,下列说法:①其图象开口向下;②其图象的对称轴为直线x=-3;③当x=3时,函数有最大值1;④当x<3时,y随x增大而减小其中正确说法的个数是( )
A.1 B.2 C.3 D.4
3.如图,平面直角坐标系中,两条抛物线有
相同的对称轴,则下列关系正确的是( )
A.m=n,k>h B.m=n,k
A
A
课堂检测
4.某广场中心有高低不同的各种喷泉,其中一支高度为1m的喷水管喷出的抛物线型水柱最大高度为3m,此时距喷水管的水平距离为 m,求在如图所示的平面直角坐标系中抛物线型水柱对应的函数解析式(不要求写出自变量的取值范围).
课堂检测
解:∵点( ,3)是抛物线的顶点,
∴可设抛物线型水柱对应的函数解析式为
y=a(x- )2+3.
∵抛物线经过点(0,1),
∴1=(0- )2 a+3,解得a=-8.
∴抛物线型水柱对应的函数解析式为:
y=-8(x- )2+3.
课堂检测
1.如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积的最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
C
拓展训练
1.利用二次函数解决实际问题中的喷水问题.
2.利用二次函数解决实际问题中的几何图形问题.
课堂小结
1.若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则所得抛物线的解析式为( )
A.y=(x+2)2+3 B.y=(x-2)2+3 C.y=(x+2)2-3 D.y=(x-2)2-3
2.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1个单位,得到抛物线的解析式为______________.
3.若y=x2+(k-2)的顶点是原点,则k____;
若顶点位于x轴上方,则k____;
若顶点位于x轴下方,则k .
B
y=-3(x-2)2+3
=2
>2
<2
课后作业
4.若函数y=3(x-4)2+k与x轴的一个交点坐标是(2,0),
则它与x轴的另一个交点坐标是 .
5.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-1)2+1的
图象上,若x1>x2>1,则y1 y2(填“>”“=”“<”).
(6,0)
>
课后作业
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
