7.1.2三角形的中线,角平分线与高线[下学期]
文档属性
| 名称 | 7.1.2三角形的中线,角平分线与高线[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 293.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-08 11:32:00 | ||
图片预览


文档简介
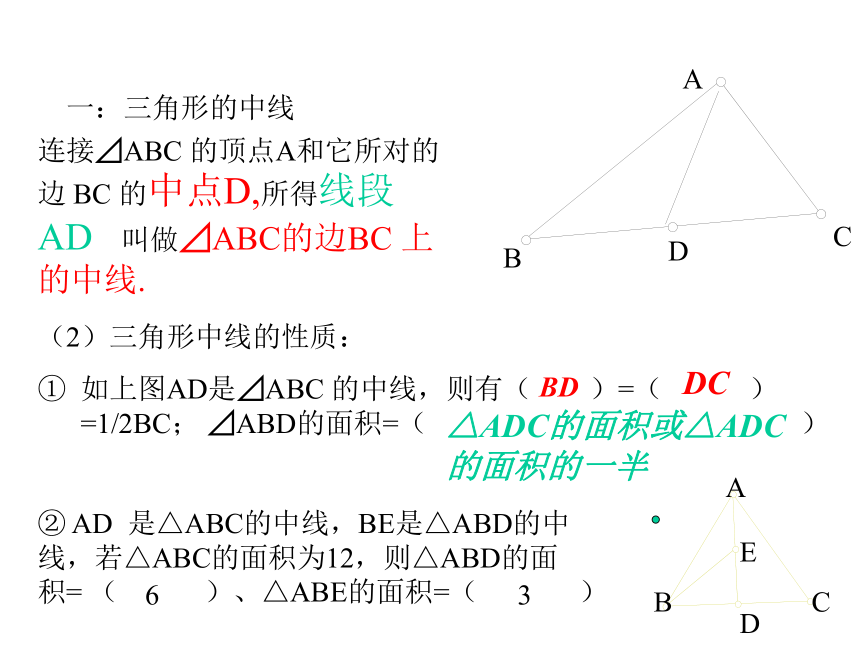
课件10张PPT。§7.1 .2三角形的中线、角平分线与高线一:三角形的中线ABC连接⊿ABC 的顶点A和它所对的边 BC 的中点D,所得线段 AD 叫做⊿ABC的边BC 上的中线.D(2)三角形中线的性质:
如上图AD是⊿ABC 的中线,则有( )=( )=1/2BC; ⊿ABD的面积=( ) BDDC△ADC的面积或△ADC的面积的一半② AD 是△ABC的中线,BE是△ABD的中线,若△ABC的面积为12,则△ABD的面积= ( )、△ABE的面积=( )ABCDE63一位同学画三角形的中线时,其中两边的中线交于点G,
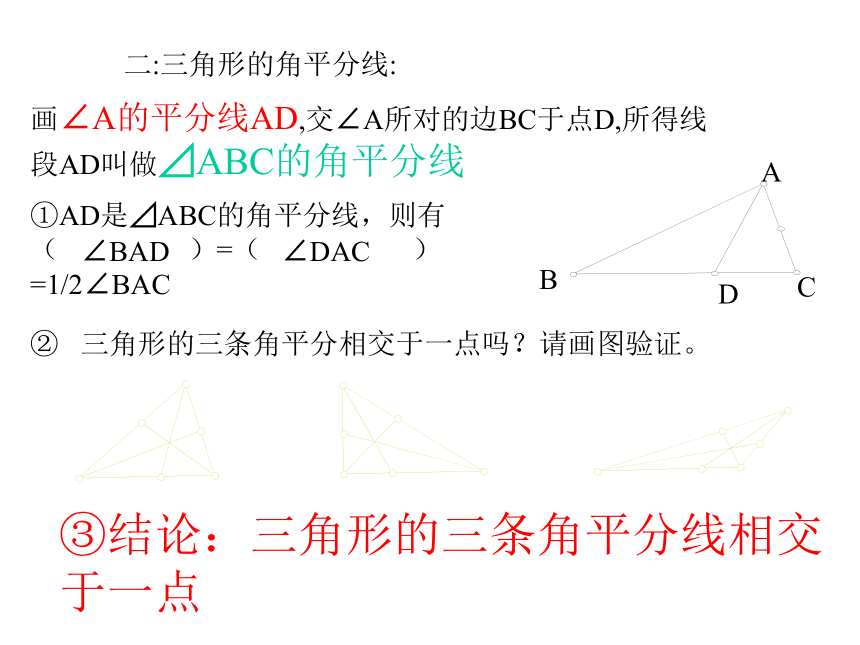
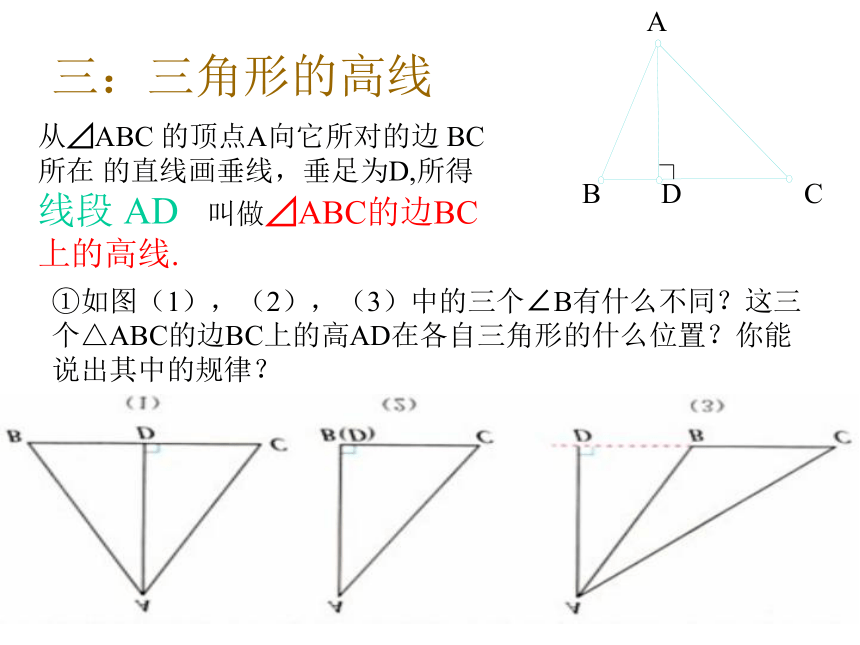
发现第三条边上的中线也通过G点,是否所有的三角形三条边上的中线也如此,请你动手试一试?ABCDEFG 结论:三角形的三边中线相交于一点二:三角形的角平分线:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做⊿ABC的角平分线ABCD①AD是⊿ABC的角平分线,则有( )=( )=1/2∠BAC∠BAD∠DAC② 三角形的三条角平分相交于一点吗?请画图验证。③结论:三角形的三条角平分线相交于一点三:三角形的高线从⊿ABC 的顶点A向它所对的边 BC所在 的直线画垂线,垂足为D,所得线段 AD 叫做⊿ABC的边BC 上的高线.ABCD①如图(1),(2),(3)中的三个∠B有什么不同?这三个△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律?C②三角形的三条角平分线、中线都相交于一点,有同学猜测三角形的三条高线所在直线 也相交于一点?你认为对吗?请动手试一试.③结论:三角形的三条高线相交于一点.直角三角形有两条高线是直角边,钝角三角形有两条高线在三角形的外部.四:巩固练习:
1:下列说法
①三角形的高线、中线、角平分线都是线段;
②三角形的高线、中线、角平分线都在三角形的内部;
③三角形的高线、中线、角平分线都相交于一点;
④直角三角形的高线只有一条;其中正确的个数是( )
A 1 B 2 C 3 D 4
B2:如图, △ABC中,AB=2㎝,BC=4 ㎝。 △ABC的高AD 与CE的比是多少?
ABCDE解:由三角形的面积公式知; AD/EC=4:2AFDCAC∠2∠ABC∠4如图,AD是△ABC的角平分线。DE∥AC, DE交AB于E,DF交AC于F.图中∠ADE与∠ADF有什么关系?为什么?ABCDEF小结
如上图AD是⊿ABC 的中线,则有( )=( )=1/2BC; ⊿ABD的面积=( ) BDDC△ADC的面积或△ADC的面积的一半② AD 是△ABC的中线,BE是△ABD的中线,若△ABC的面积为12,则△ABD的面积= ( )、△ABE的面积=( )ABCDE63一位同学画三角形的中线时,其中两边的中线交于点G,
发现第三条边上的中线也通过G点,是否所有的三角形三条边上的中线也如此,请你动手试一试?ABCDEFG 结论:三角形的三边中线相交于一点二:三角形的角平分线:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做⊿ABC的角平分线ABCD①AD是⊿ABC的角平分线,则有( )=( )=1/2∠BAC∠BAD∠DAC② 三角形的三条角平分相交于一点吗?请画图验证。③结论:三角形的三条角平分线相交于一点三:三角形的高线从⊿ABC 的顶点A向它所对的边 BC所在 的直线画垂线,垂足为D,所得线段 AD 叫做⊿ABC的边BC 上的高线.ABCD①如图(1),(2),(3)中的三个∠B有什么不同?这三个△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律?C②三角形的三条角平分线、中线都相交于一点,有同学猜测三角形的三条高线所在直线 也相交于一点?你认为对吗?请动手试一试.③结论:三角形的三条高线相交于一点.直角三角形有两条高线是直角边,钝角三角形有两条高线在三角形的外部.四:巩固练习:
1:下列说法
①三角形的高线、中线、角平分线都是线段;
②三角形的高线、中线、角平分线都在三角形的内部;
③三角形的高线、中线、角平分线都相交于一点;
④直角三角形的高线只有一条;其中正确的个数是( )
A 1 B 2 C 3 D 4
B2:如图, △ABC中,AB=2㎝,BC=4 ㎝。 △ABC的高AD 与CE的比是多少?
ABCDE解:由三角形的面积公式知; AD/EC=4:2AFDCAC∠2∠ABC∠4如图,AD是△ABC的角平分线。DE∥AC, DE交AB于E,DF交AC于F.图中∠ADE与∠ADF有什么关系?为什么?ABCDEF小结
