三角形的高.中线和角平分线[下学期]
文档属性
| 名称 | 三角形的高.中线和角平分线[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 853.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-29 00:00:00 | ||
图片预览


文档简介
(共38张PPT)
三角形的高、中线和角平分线
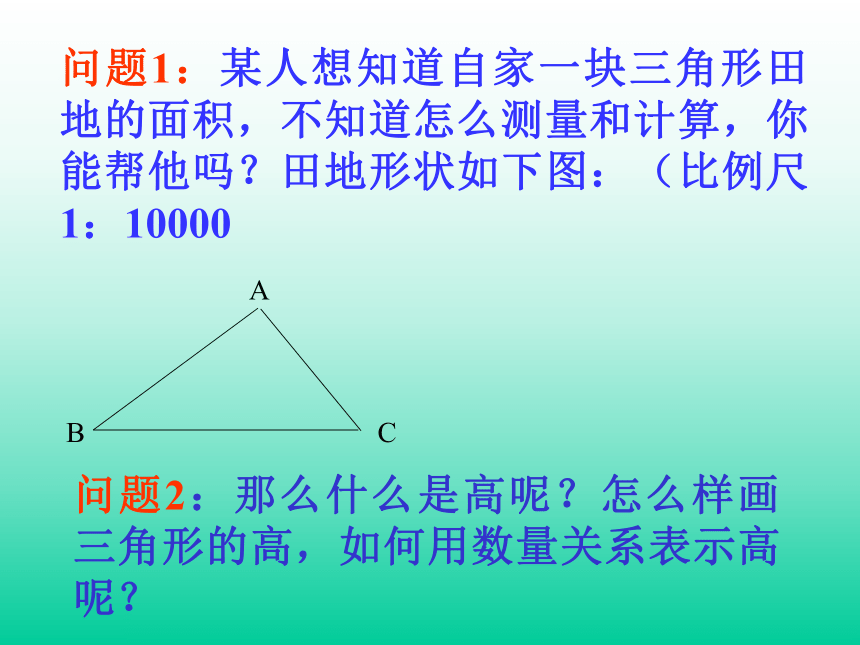
问题1:某人想知道自家一块三角形田地的面积,不知道怎么测量和计算,你能帮他吗?田地形状如下图:(比例尺1:10000
A
B
C
问题2:那么什么是高呢?怎么样画三角形的高,如何用数量关系表示高呢?
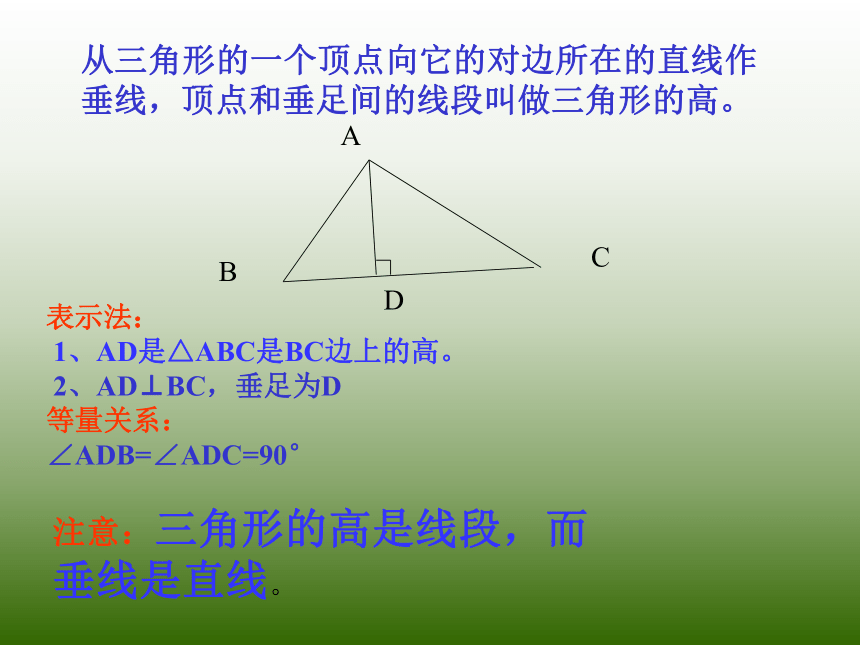
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足间的线段叫做三角形的高。
表示法:
1、AD是△ABC是BC边上的高。
2、AD⊥BC,垂足为D
等量关系:
∠ADB=∠ADC=90°
A
B
C
D
注意:三角形的高是线段,而垂线是直线。
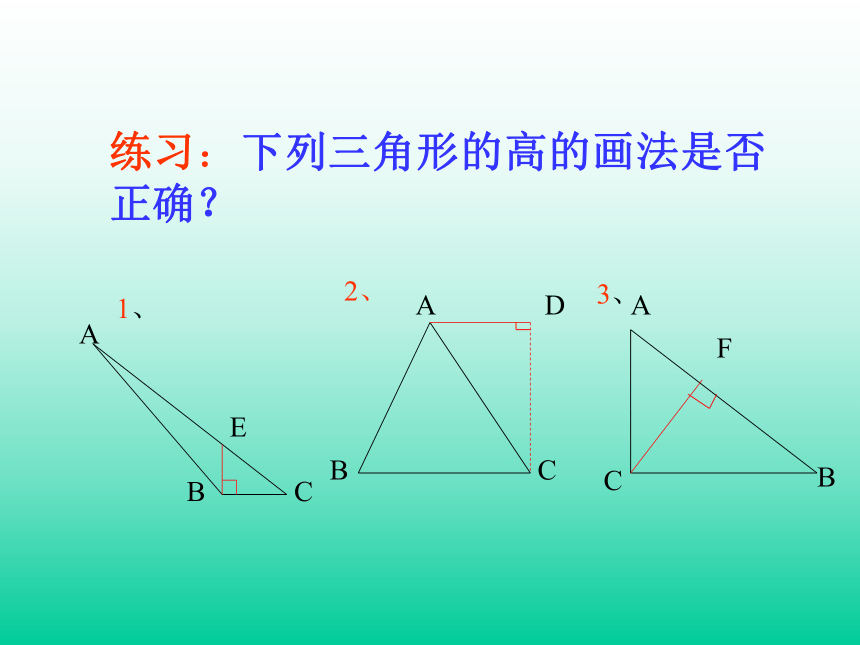
练习:下列三角形的高的画法是否正确?
1、
2、
3、
A
B
E
C
A
C
B
D
A
C
B
F
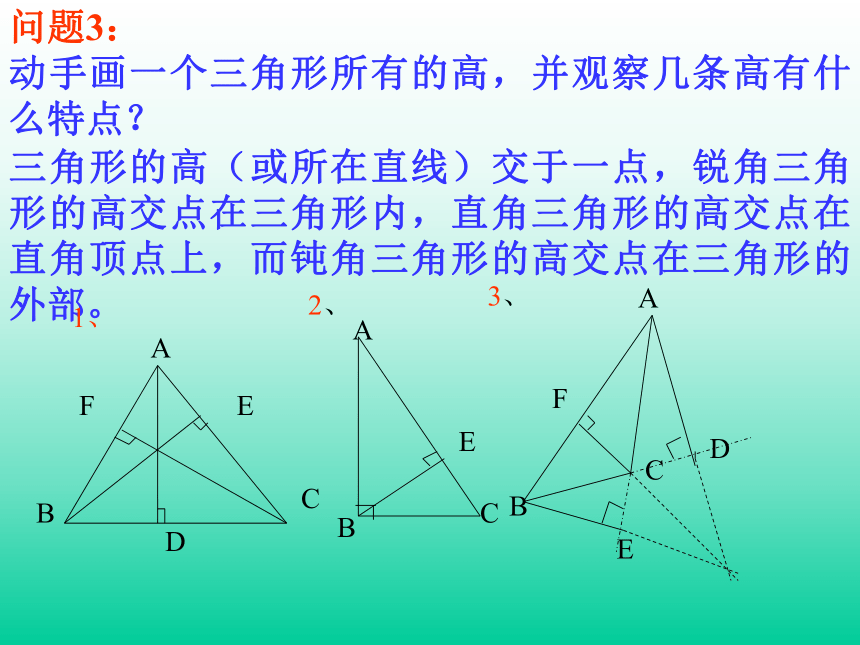
三角形的高(或所在直线)交于一点,锐角三角形的高交点在三角形内,直角三角形的高交点在直角顶点上,而钝角三角形的高交点在三角形的外部。
1、
2、
3、
A
B
C
F
D
E
A
B
C
E
A
B
C
D
E
F
问题3:
动手画一个三角形所有的高,并观察几条高有什么特点?
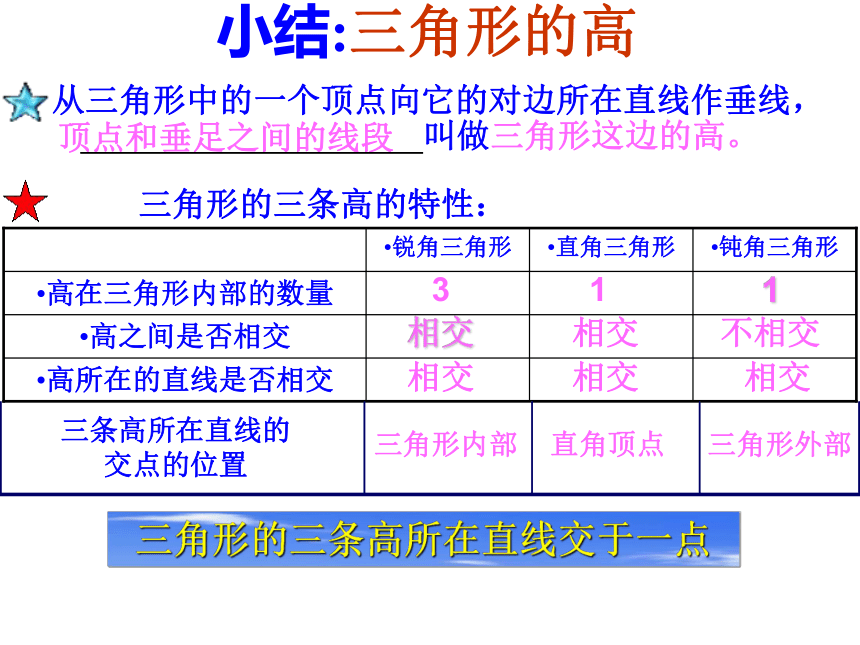
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高。
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
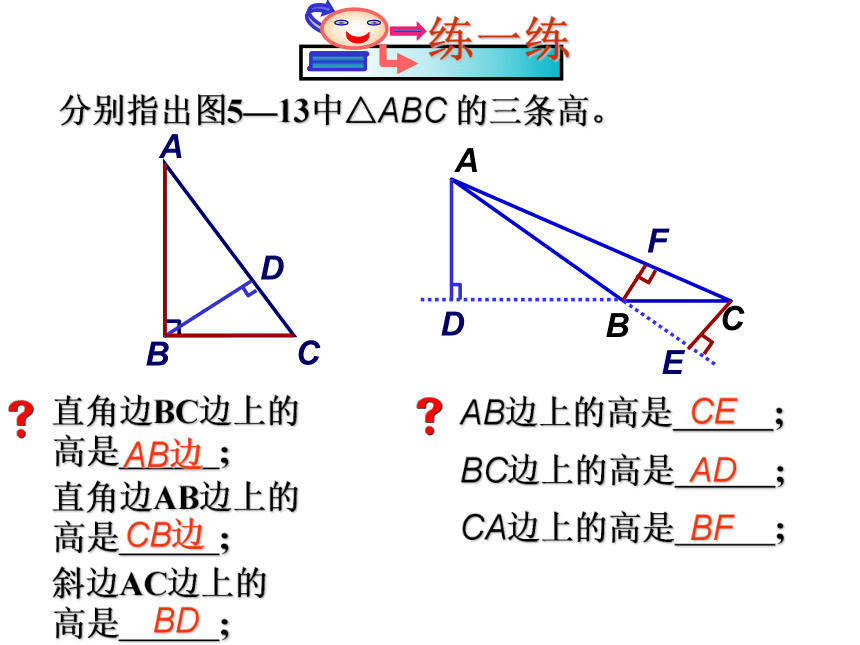
分别指出图5—13中△ABC 的三条高。
直角边BC边上的
高是 ;
AB边
直角边AB边上的
高是 ;
CB边
A
B
C
D
E
F
练一练
A
B
C
D
斜边AC边上的
高是 ;
BD
AB边上的高是 ;
CE
BC边上的高是 ;
AD
CA边上的高是 ;
BF
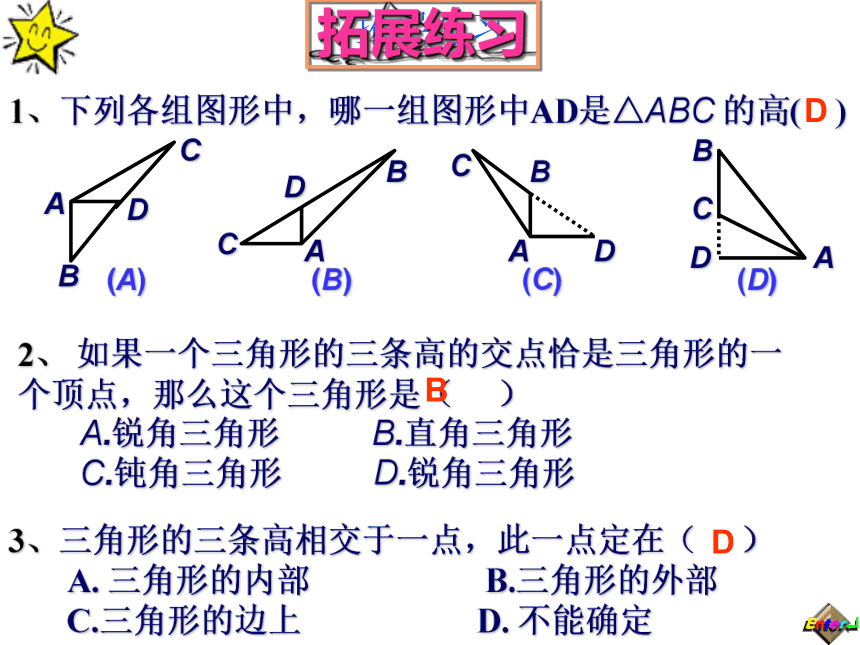
拓展练习
拓展练习
2、 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此一点定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的边上 D. 不能确定
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
D
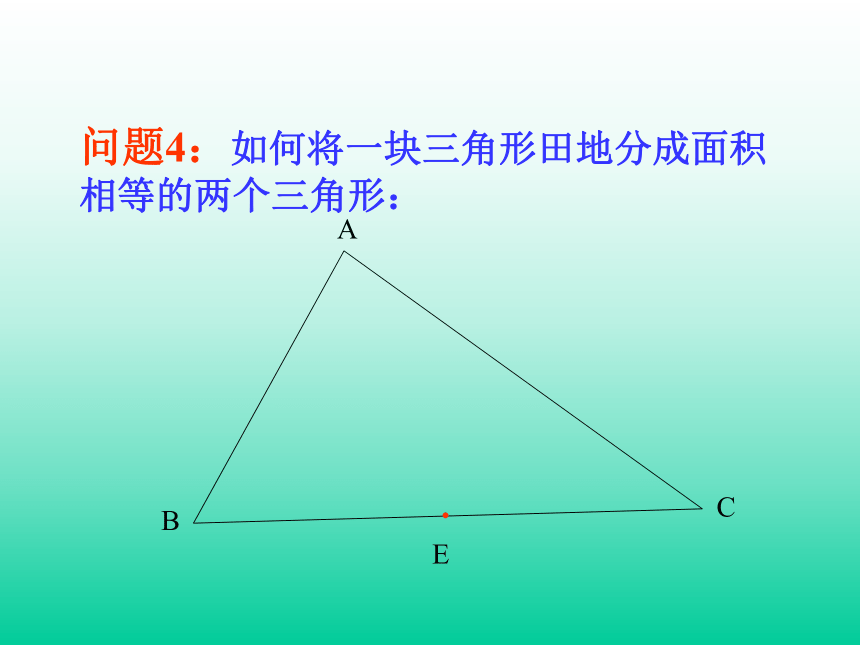
问题4:如何将一块三角形田地分成面积相等的两个三角形:
A
B
C
·
E
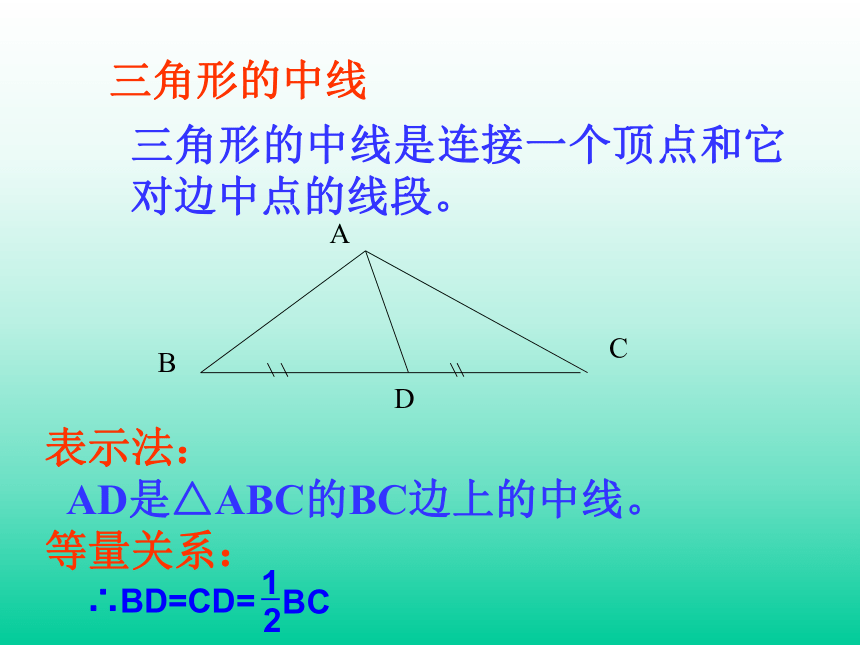
三角形的中线是连接一个顶点和它对边中点的线段。
三角形的中线
表示法:
AD是△ABC的BC边上的中线。
等量关系:
A
B
D
C
∴BD=CD=
1
2
BC
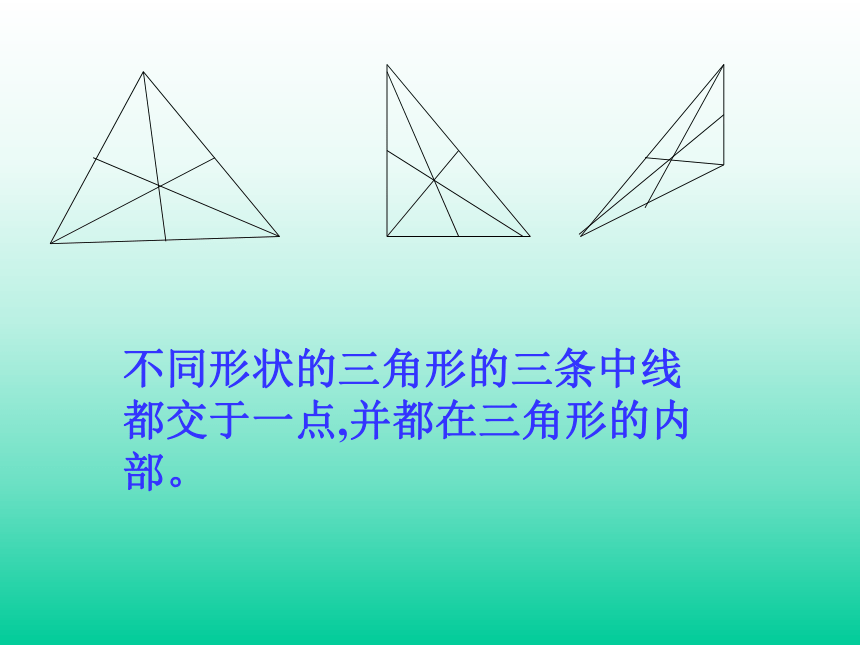
问题5:类似的,作出不同形
状三角形的所有中线,观察它们之间有何特点?
不同形状的三角形的三条中线都交于一点,并都在三角形的内部。
A
三角形的三条中线交于一点
C
B
F
E
D
O
其中,AB边上的中线是______
BC边上的中线是______
AC边上的中线是______
CF
BE
AD
∵BE是中线
∴____=_____= _____
∴AB=2______=2_______
∵CF是中线
AE
CE
AC
AF
BF
问题6、有一张三角形的纸片,如下图,通过折叠,将点B放到边AC上,观察折线有何特点。
A
B
C
三角形的角平分线是三角形的一个内角的角平分线与它对边相交,这个角的顶点与对边交点的之间的线段。
表示法:
AM是△ABC的角平分线。
等量关系:
∠1=∠2=1/2∠BAC。
A
B
C
M
1
2
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴____=_____= _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的角平分线与角的 平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线
角平分线的理解
练习
如图,AE是 △ ABC的角平分线.已知
∠B=450, ∠ C=600 ,求下列角的大小.
C
A
B
E
∠ CAE=_____
∠ AEB=_____
37.50
97.50
问题7:画出不同形状三角形的角平分线,观察有何特点。
不同形状三角形的角平分线都交于一点,交点在三角形内部。
练习
1、如图,(1),(2)和(3)中的三个∠B有什么不同?这三个⊿ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?
A
B
C
D
A
B
C
(D)
D
A
B
C
当∠B是锐角时,高AD在⊿ABC的内部
当∠B是直角时,高AD与边AB重合,
当∠B是钝角时,高AD的垂足在CB的延长线上,高AD 在⊿ABC的外部。
答案 (1),(2)和(3)中的∠B分别是锐角,直角,钝角。
现在做中考题
如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是⊿ABE的角平分线 ( )
②BE是⊿ABD边AD上的中线 ( )
③BE是⊿ABC边AC上的中线 ( )
④CH是⊿ACD边AD上的高 ( )
三角形的高、中线与角平分线都是线段
×
×
×
√
1、下列各个图形中,哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
练一练
2、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
D
3.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BE
∠CAD
∠BAC
∠AFC
BC AF
随堂练习
1.三角形的三条高线中( )
A.最多有一条在三角形的内部
B.至少有一条在三角形的内部
C.每一条都在三角形的内部
D.每一条都在三角形的外部
2.如果一个三角形的三条高线的交点恰是一个三角形的顶点,那么这个三角形是( )
A.锐角三角形 B. 直角三角形
C.钝角三角形 D.以上答案都不对
3.钝角三角形的高在三角形外的数目有( )
A.0 B.1 C.2 D.3
4.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B. 面积相等的三角形
C.直角三角形 D. 周长相等的三角形
1、三角形一边上的高( )
A、在三角形的内部 B、在三角形的外部
C、在三角形的一边上
D、以上三种情况都有可能
2、三角形的角平分线、中线、高中( )
A、每一条都是线段
B、角平分线是射线,其余是线段
C、高线是直线,其余是线段
D、高线是直线,角平分线是射线,中线是线段
四、随堂小练
D
A
3、一定在三角形内部的线段是( )
A、三角形的角平分线、中线、高
B、 三角形的三条高
C、三角形的角平分线、中线
D、以上都不对
4、三角形的三条边之比4:5:6,则对应高之比为( )
A 、6:5:4 B、4:5:6
C、 10:12:15 D、15:12:10
C
D
5、如图:AD是ABC的中线,则S△ABD S△ADC
A
B
C
D
=
(2003,昆明)一个三角形的两条高既不在三角形内,又不在三角形外,这个三角形是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、不确定
C
中考链接
例二
如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )
①AD是△ABE的角平分线;
②BE是△ABD边AD上的中线;
③CH为△ACD边AD上的高。
1个 B. 2个
C. 3个 D. 0个
A
B
C
D
E
F
G
H
1
2
A
提高题
⑴在△ABC中, AD是BC边上的中线,△ADC的周长比△ABD的周长多3cm,AB与AC的和11cm,求AB的边 .
⑵ AD、AE分别是△ABC的 BC边上的中线,△ABD的周长比△ADC的周长多3cm,AB=5,求AC的长以及△ABD与△ADC的面积关系.
⑶在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm的两部分,求三角形的各边.
在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
如图,在ΔABC中,角平分线BD、CE相交于点O, 计算:
(1)当∠A=50°时,求∠BOC;
A
O
D
E
B
C
(3)如果设∠A为α,求∠BOC(用α表示)
(2)当∠BOC=130°时,求∠A.
共同点:三角形的高、角平分线、中线,都有三条,都是线段,都交于一点。
不同点:三角形的高所在位置与三角形的形状有关,而不论何种形状三角形,它的角平分线、中线,都在三角形的内部。
布置作业:
课本P77页第3 、4两题
小结:本节课所学三角形三条重要线段的共同点和不同点
这节课你有那些收获
有哪些困惑
三角形的高、中线和角平分线
问题1:某人想知道自家一块三角形田地的面积,不知道怎么测量和计算,你能帮他吗?田地形状如下图:(比例尺1:10000
A
B
C
问题2:那么什么是高呢?怎么样画三角形的高,如何用数量关系表示高呢?
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足间的线段叫做三角形的高。
表示法:
1、AD是△ABC是BC边上的高。
2、AD⊥BC,垂足为D
等量关系:
∠ADB=∠ADC=90°
A
B
C
D
注意:三角形的高是线段,而垂线是直线。
练习:下列三角形的高的画法是否正确?
1、
2、
3、
A
B
E
C
A
C
B
D
A
C
B
F
三角形的高(或所在直线)交于一点,锐角三角形的高交点在三角形内,直角三角形的高交点在直角顶点上,而钝角三角形的高交点在三角形的外部。
1、
2、
3、
A
B
C
F
D
E
A
B
C
E
A
B
C
D
E
F
问题3:
动手画一个三角形所有的高,并观察几条高有什么特点?
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高。
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
分别指出图5—13中△ABC 的三条高。
直角边BC边上的
高是 ;
AB边
直角边AB边上的
高是 ;
CB边
A
B
C
D
E
F
练一练
A
B
C
D
斜边AC边上的
高是 ;
BD
AB边上的高是 ;
CE
BC边上的高是 ;
AD
CA边上的高是 ;
BF
拓展练习
拓展练习
2、 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此一点定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的边上 D. 不能确定
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
B
D
D
问题4:如何将一块三角形田地分成面积相等的两个三角形:
A
B
C
·
E
三角形的中线是连接一个顶点和它对边中点的线段。
三角形的中线
表示法:
AD是△ABC的BC边上的中线。
等量关系:
A
B
D
C
∴BD=CD=
1
2
BC
问题5:类似的,作出不同形
状三角形的所有中线,观察它们之间有何特点?
不同形状的三角形的三条中线都交于一点,并都在三角形的内部。
A
三角形的三条中线交于一点
C
B
F
E
D
O
其中,AB边上的中线是______
BC边上的中线是______
AC边上的中线是______
CF
BE
AD
∵BE是中线
∴____=_____= _____
∴AB=2______=2_______
∵CF是中线
AE
CE
AC
AF
BF
问题6、有一张三角形的纸片,如下图,通过折叠,将点B放到边AC上,观察折线有何特点。
A
B
C
三角形的角平分线是三角形的一个内角的角平分线与它对边相交,这个角的顶点与对边交点的之间的线段。
表示法:
AM是△ABC的角平分线。
等量关系:
∠1=∠2=1/2∠BAC。
A
B
C
M
1
2
A
C
B
F
E
D
O
∵BE是△ABC的角平分线
∴____=_____= _____
∴∠ACB=2______=2______
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线
∠BCF
三角形的角平分线与角的 平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线
角平分线的理解
练习
如图,AE是 △ ABC的角平分线.已知
∠B=450, ∠ C=600 ,求下列角的大小.
C
A
B
E
∠ CAE=_____
∠ AEB=_____
37.50
97.50
问题7:画出不同形状三角形的角平分线,观察有何特点。
不同形状三角形的角平分线都交于一点,交点在三角形内部。
练习
1、如图,(1),(2)和(3)中的三个∠B有什么不同?这三个⊿ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?
A
B
C
D
A
B
C
(D)
D
A
B
C
当∠B是锐角时,高AD在⊿ABC的内部
当∠B是直角时,高AD与边AB重合,
当∠B是钝角时,高AD的垂足在CB的延长线上,高AD 在⊿ABC的外部。
答案 (1),(2)和(3)中的∠B分别是锐角,直角,钝角。
现在做中考题
如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的.
⌒
⌒
A
B
C
D
E
1
2
F
G
H
①AD是⊿ABE的角平分线 ( )
②BE是⊿ABD边AD上的中线 ( )
③BE是⊿ABC边AC上的中线 ( )
④CH是⊿ACD边AD上的高 ( )
三角形的高、中线与角平分线都是线段
×
×
×
√
1、下列各个图形中,哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
练一练
2、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
D
3.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BE
∠CAD
∠BAC
∠AFC
BC AF
随堂练习
1.三角形的三条高线中( )
A.最多有一条在三角形的内部
B.至少有一条在三角形的内部
C.每一条都在三角形的内部
D.每一条都在三角形的外部
2.如果一个三角形的三条高线的交点恰是一个三角形的顶点,那么这个三角形是( )
A.锐角三角形 B. 直角三角形
C.钝角三角形 D.以上答案都不对
3.钝角三角形的高在三角形外的数目有( )
A.0 B.1 C.2 D.3
4.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B. 面积相等的三角形
C.直角三角形 D. 周长相等的三角形
1、三角形一边上的高( )
A、在三角形的内部 B、在三角形的外部
C、在三角形的一边上
D、以上三种情况都有可能
2、三角形的角平分线、中线、高中( )
A、每一条都是线段
B、角平分线是射线,其余是线段
C、高线是直线,其余是线段
D、高线是直线,角平分线是射线,中线是线段
四、随堂小练
D
A
3、一定在三角形内部的线段是( )
A、三角形的角平分线、中线、高
B、 三角形的三条高
C、三角形的角平分线、中线
D、以上都不对
4、三角形的三条边之比4:5:6,则对应高之比为( )
A 、6:5:4 B、4:5:6
C、 10:12:15 D、15:12:10
C
D
5、如图:AD是ABC的中线,则S△ABD S△ADC
A
B
C
D
=
(2003,昆明)一个三角形的两条高既不在三角形内,又不在三角形外,这个三角形是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、不确定
C
中考链接
例二
如下图,在△ABC中,∠1=∠2,G为
AD的中点,延长BG交AC于E,F为
AB上一点,CF⊥AD于H,下面判断
正确的有( )
①AD是△ABE的角平分线;
②BE是△ABD边AD上的中线;
③CH为△ACD边AD上的高。
1个 B. 2个
C. 3个 D. 0个
A
B
C
D
E
F
G
H
1
2
A
提高题
⑴在△ABC中, AD是BC边上的中线,△ADC的周长比△ABD的周长多3cm,AB与AC的和11cm,求AB的边 .
⑵ AD、AE分别是△ABC的 BC边上的中线,△ABD的周长比△ADC的周长多3cm,AB=5,求AC的长以及△ABD与△ADC的面积关系.
⑶在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm的两部分,求三角形的各边.
在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
如图,在ΔABC中,角平分线BD、CE相交于点O, 计算:
(1)当∠A=50°时,求∠BOC;
A
O
D
E
B
C
(3)如果设∠A为α,求∠BOC(用α表示)
(2)当∠BOC=130°时,求∠A.
共同点:三角形的高、角平分线、中线,都有三条,都是线段,都交于一点。
不同点:三角形的高所在位置与三角形的形状有关,而不论何种形状三角形,它的角平分线、中线,都在三角形的内部。
布置作业:
课本P77页第3 、4两题
小结:本节课所学三角形三条重要线段的共同点和不同点
这节课你有那些收获
有哪些困惑
