沪科版九年级上册数学第一次月考试卷(含答案)
文档属性
| 名称 | 沪科版九年级上册数学第一次月考试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 15:19:30 | ||
图片预览

文档简介
沪科版九年级上册数学第一次月考试题
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列函数中,是二次函数的是( )
A. B.
C. D.
2.抛物线y=3(x﹣2)2+5的顶点坐标是( )
A.(﹣2,5) B.(﹣2,﹣5) C.(2,5) D.(2,﹣5)
3.用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )
A.y=(x﹣4)2+7 B.y=(x+4)2+7
C.y=(x﹣4)2﹣25 D.y=(x+4)2﹣25
4.在平面直角坐标系中,抛物线先向下平移2个单位,再向左平移2个单位,则平移后抛物线对应的函数表达式是( )
A. B.
C. D.
5.若双曲线过点、,则与的大小关系为( )
A. B.
C. D.与的大小无法确定
6.二次函数与的图象与x轴有交点,则k的取值范围是
A. B.且
C. D.且
7.铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式为y=-x2+x+.则该运动员此次掷铅球的成绩是( )
A.6 m B.12 m C.8 m D.10 m
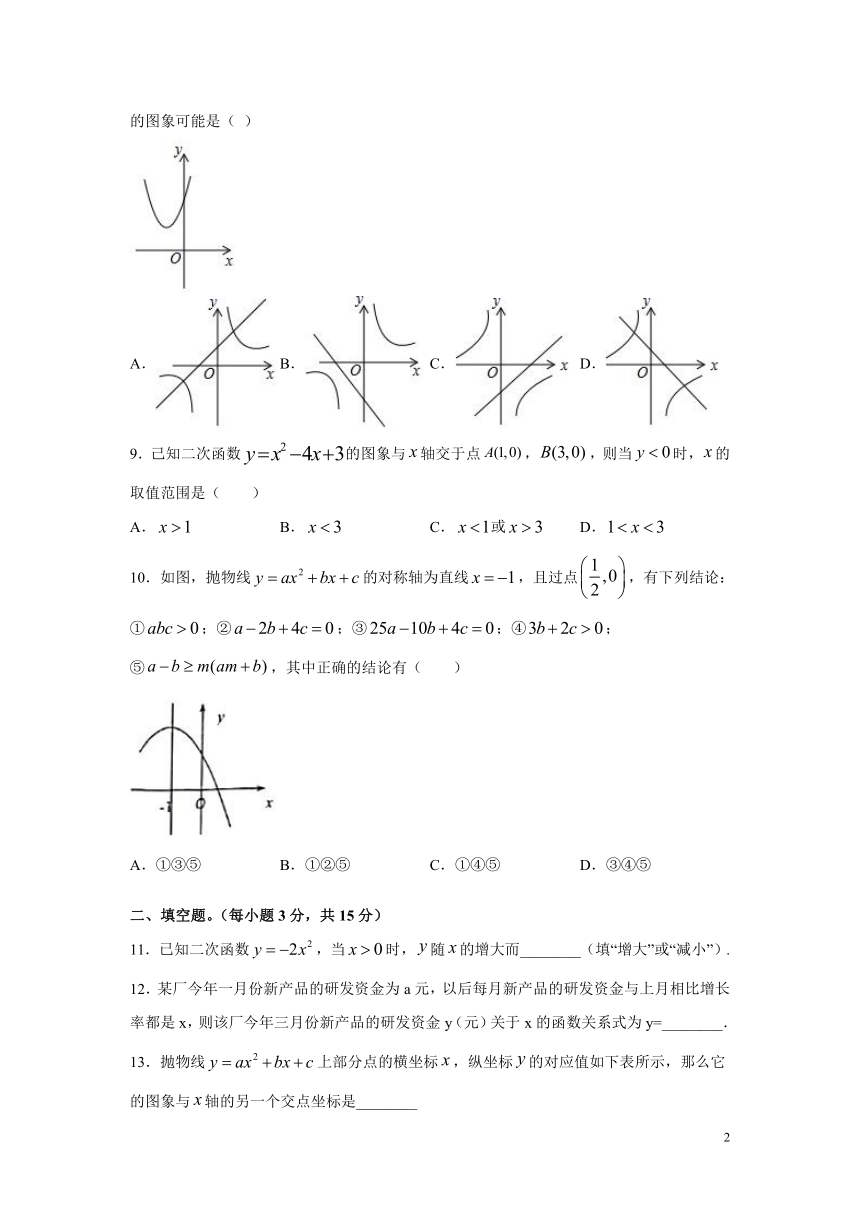
8.已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A. B. C. D.
9.己知二次函数的图象与轴交于点,,则当时,的取值范围是( )
A. B. C.或 D.
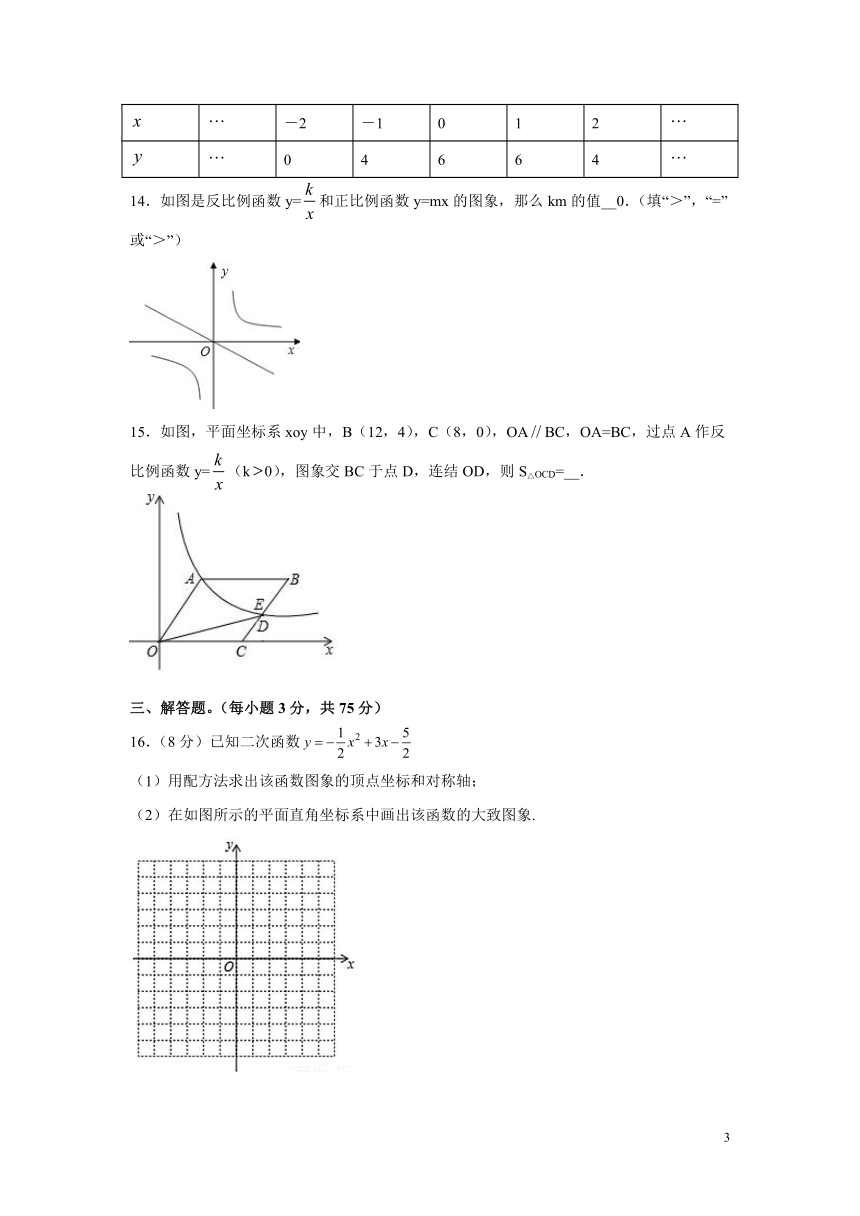
10.如图,抛物线的对称轴为直线,且过点,有下列结论:
①;②;③;④;⑤,其中正确的结论有( )
A.①③⑤ B.①②⑤ C.①④⑤ D.③④⑤
二、填空题。(每小题3分,共15分)
11.已知二次函数,当时,随的增大而________(填“增大”或“减小”).
12.某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=________.
13.抛物线上部分点的横坐标,纵坐标的对应值如下表所示,那么它的图象与轴的另一个交点坐标是________
-2 -1 0 1 2
0 4 6 6 4
14.如图是反比例函数y=和正比例函数y=mx的图象,那么km的值__0.(填“>”,“=”或“>”)
15.如图,平面坐标系xoy中,B(12,4),C(8,0),OABC,OA=BC,过点A作反比例函数y=(k0),图象交BC于点D,连结OD,则S△OCD=__.
三、解答题。(每小题3分,共75分)
16.(8分)已知二次函数
(1)用配方法求出该函数图象的顶点坐标和对称轴;
(2)在如图所示的平面直角坐标系中画出该函数的大致图象.
17.(5分)已知二次函数图像的顶点坐标为(1,-1),且经过原点(0,0),求该函数的解析式.
18.(8分)足球赛是同学们比较喜欢的体育比赛.你知道吗,一个足球被从地面向上踢出,它距地面的高度可以用二次函数刻画,其中表示足球被踢出后经过的时间.
(1)方程的根的实际意义是________.
(2)问经过多长时间,足球到达它的最高点?最高点的高度是多少?
19.(5分)关于x的函数y=(m2-1)x2-(2m+2)x+2的图象与x轴只有一个公共点,求m的值.
20.(9分)如图,已知反比例函数y1=的图象与一次函数y2=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)直接写出y2>y1时自变量x的取值范围.
21.(8分)已知抛物线的对称轴为直线,且抛物线经过点,它与轴的另一交点为,与轴的交点为.
(1)求这条抛物线所对应的函数表达式;
(2)在直线上求点,使的周长最小,并求出的周长.
22.(12分)实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间(时)的关系可近似地用二次函数刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值 最大值为多少
②当=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班 请说明理由.
23.(10分)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少
24.(10分)如图,地物线点:(、、均不为0)的顶点为,与轴的交点为,我们称以为顶点,对称轴是轴且过点的抛物线为抛物线的衍生抛物线,直线为抛物线的衍生直线.
(1)求抛物线的衍生抛物线和衍生直线的解析式;
(2)若一条抛物线的衍生抛物线和衍生直线分别是和,求这条抛物线的解析式.
参考答案
1.C
2.C
3.C
4.B
5.A
6.D
7.D
8.C
9.D
10.A
11.减小
12.a(1+x)2
13.
14.
15.
16.(1); (2)答案见解析
17.y=(x-1)2-1
18.(1)足球离开地面的时间,足球落地的时间 (2);
19.1或3.
20.(1)反比例函数解析式为y1=,一次函数得到解析式为y2=x+3;(2)7.5;(3)当﹣4<x<0或x>1时,y2>y1
21.(1) (2)
22.(1)①200;②225;(2)不能,理由见解析.
23.(1)W1=-2x +60x+8000,W2=-19x+950;(2)当x=10时,W总最大为9160元.
24.(1); (2)
(
2
)
(
1
)
一、选择题。(每小题只有一个正确答案,每小题3分,共30分)
1.下列函数中,是二次函数的是( )
A. B.
C. D.
2.抛物线y=3(x﹣2)2+5的顶点坐标是( )
A.(﹣2,5) B.(﹣2,﹣5) C.(2,5) D.(2,﹣5)
3.用配方法将二次函数y=x2﹣8x﹣9化为y=a(x﹣h)2+k的形式为( )
A.y=(x﹣4)2+7 B.y=(x+4)2+7
C.y=(x﹣4)2﹣25 D.y=(x+4)2﹣25
4.在平面直角坐标系中,抛物线先向下平移2个单位,再向左平移2个单位,则平移后抛物线对应的函数表达式是( )
A. B.
C. D.
5.若双曲线过点、,则与的大小关系为( )
A. B.
C. D.与的大小无法确定
6.二次函数与的图象与x轴有交点,则k的取值范围是
A. B.且
C. D.且
7.铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式为y=-x2+x+.则该运动员此次掷铅球的成绩是( )
A.6 m B.12 m C.8 m D.10 m
8.已知二次函数y=(x+m)2–n的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A. B. C. D.
9.己知二次函数的图象与轴交于点,,则当时,的取值范围是( )
A. B. C.或 D.
10.如图,抛物线的对称轴为直线,且过点,有下列结论:
①;②;③;④;⑤,其中正确的结论有( )
A.①③⑤ B.①②⑤ C.①④⑤ D.③④⑤
二、填空题。(每小题3分,共15分)
11.已知二次函数,当时,随的增大而________(填“增大”或“减小”).
12.某厂今年一月份新产品的研发资金为a元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=________.
13.抛物线上部分点的横坐标,纵坐标的对应值如下表所示,那么它的图象与轴的另一个交点坐标是________
-2 -1 0 1 2
0 4 6 6 4
14.如图是反比例函数y=和正比例函数y=mx的图象,那么km的值__0.(填“>”,“=”或“>”)
15.如图,平面坐标系xoy中,B(12,4),C(8,0),OABC,OA=BC,过点A作反比例函数y=(k0),图象交BC于点D,连结OD,则S△OCD=__.
三、解答题。(每小题3分,共75分)
16.(8分)已知二次函数
(1)用配方法求出该函数图象的顶点坐标和对称轴;
(2)在如图所示的平面直角坐标系中画出该函数的大致图象.
17.(5分)已知二次函数图像的顶点坐标为(1,-1),且经过原点(0,0),求该函数的解析式.
18.(8分)足球赛是同学们比较喜欢的体育比赛.你知道吗,一个足球被从地面向上踢出,它距地面的高度可以用二次函数刻画,其中表示足球被踢出后经过的时间.
(1)方程的根的实际意义是________.
(2)问经过多长时间,足球到达它的最高点?最高点的高度是多少?
19.(5分)关于x的函数y=(m2-1)x2-(2m+2)x+2的图象与x轴只有一个公共点,求m的值.
20.(9分)如图,已知反比例函数y1=的图象与一次函数y2=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求反比例函数和一次函数的表达式;
(2)求△OAB的面积;
(3)直接写出y2>y1时自变量x的取值范围.
21.(8分)已知抛物线的对称轴为直线,且抛物线经过点,它与轴的另一交点为,与轴的交点为.
(1)求这条抛物线所对应的函数表达式;
(2)在直线上求点,使的周长最小,并求出的周长.
22.(12分)实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间(时)的关系可近似地用二次函数刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值 最大值为多少
②当=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班 请说明理由.
23.(10分)小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少
24.(10分)如图,地物线点:(、、均不为0)的顶点为,与轴的交点为,我们称以为顶点,对称轴是轴且过点的抛物线为抛物线的衍生抛物线,直线为抛物线的衍生直线.
(1)求抛物线的衍生抛物线和衍生直线的解析式;
(2)若一条抛物线的衍生抛物线和衍生直线分别是和,求这条抛物线的解析式.
参考答案
1.C
2.C
3.C
4.B
5.A
6.D
7.D
8.C
9.D
10.A
11.减小
12.a(1+x)2
13.
14.
15.
16.(1); (2)答案见解析
17.y=(x-1)2-1
18.(1)足球离开地面的时间,足球落地的时间 (2);
19.1或3.
20.(1)反比例函数解析式为y1=,一次函数得到解析式为y2=x+3;(2)7.5;(3)当﹣4<x<0或x>1时,y2>y1
21.(1) (2)
22.(1)①200;②225;(2)不能,理由见解析.
23.(1)W1=-2x +60x+8000,W2=-19x+950;(2)当x=10时,W总最大为9160元.
24.(1); (2)
(
2
)
(
1
)
同课章节目录
